带内双频电磁辐射对频率步进连续波雷达的虚警干扰规律
2023-06-10魏光辉赵宏泽郑建拥
赵 凯,魏光辉,杜 雪,赵宏泽,郑建拥
(1. 陆军工程大学石家庄校区 电磁环境效应国家重点实验室, 河北 石家庄 050003; 2. 中国人民解放军63870部队, 陕西 华阴 714200)
随着武器装备的信息化,用频装备辐射功率、接收灵敏度不断提高,电子战系统、电磁脉冲弹和高功率微波发展迅猛,使得未来信息化战争中战场电磁环境日趋复杂、恶劣[1]。信息化装备能否具有良好的电磁环境适应性,已成为战场情报侦察、目标探测识别、联合指挥控制、武器精确打击以及多军兵种协同作战的决定性因素,直接影响着信息化武器系统的作战效能,乃至战争成败。
雷达作为战场“千里眼”,电子化程度极高对外部电磁辐射较为敏感,若电磁防护性能不足,就难以正常发挥战技性能[2]。针对雷达受电磁干扰的研究主要以雷达电子对抗为背景,雷达有源干扰效应可粗略分为遮盖性干扰与欺骗性干扰,其中欺骗性干扰是将类似于目标回波的乱真信号作用于雷达,诱导雷达产生误判断或使其无法识别真实目标[3-4],属于信息干扰效应,这方面的研究可参见文献[5-10]。而对于以非信息干扰为背景的研究,文献[11]通过仿真调频连续波雷达信号处理过程得到,当频率处于雷达工作频带内时,外部单频连续波信号会导致雷达出现“距离-速度谱”干扰带。文献[12-13]结合效应试验,针对单频电磁辐射对雷达的干扰效应规律进行研究,认为单频电磁辐射不仅对雷达造成阻塞干扰,而且还会在不同的探测距离出现乱真目标。由此给出虚警干扰的概念,即单频电磁辐射与有用信号相互作用产生的交调信号或多频电磁辐射相互作用产生的互调信号被受试雷达直接作为有用信号进行处理,使受试雷达产生虚假目标的现象。由于虚警干扰比阻塞干扰对辐射场强的要求更低[12],掌握多频电磁辐射对雷达的虚警干扰规律,是客观评价雷达装备抗电磁干扰能力的重要前提。
对此,本文以频率步进连续波雷达为研究对象,从装备电磁辐射效应机理出发,首先理论分析了双频电磁辐射对雷达的虚警干扰规律,而后通过开展效应试验对理论分析结果进行验证与补充。本着有限目标原则,只研究双频电磁辐射对雷达的直接作用,不涉及各类信号交调、互调造成的额外干扰效应。
1 理论分析
1.1 虚警目标电平变化规律
假设雷达在双频电磁辐射干扰下对单个静止目标进行探测,考虑一般情况,接收机前端的输入信号[12]可表示为
ur(t)=AsEscos[ωs(t-τ)+η]+A1E1cos(ω1t+φ1)+A2E2cos(ω2t+φ2)
(1)
式中:As、A1、A2分别为系统对有用信号、双频干扰信号的频率选择系数;Es、E1、E2分别为有用信号、双频干扰信号的场强幅值;ωs、ω1、ω2分别为有用信号、双频干扰信号的角频率;η、φ1、φ2分别为有用信号、双频干扰信号的初相位;τ为目标回波的时延。定义AsEs为有用信号的有效电平,A1E1与A2E2为双频电磁辐射耦合至接收机后两干扰分量的有效电平。
雷达接收机本振信号频率与回波信号频率相同,其形式可表示为
uL(t)=cosωst
(2)
当输入信号ur(t)幅值较小时,接收机处于线性工作状态,目标回波信号与双频干扰信号经放大、混频、滤波等过程后,输出双频干扰信号分量为
ur(t)uL(t)→b1A1E1cos[(ω1-ωs)t+φ1-η]+b1A2E2cos[(ω2-ωs)t+φ2-η]
(3)
其中,b1为非线性系数中的线性项[12]。
在后续的信号处理中,I/Q通道混频输出的双频干扰分量会导致系统误判,进而产生两个虚警目标;虚警目标的形成机理与单频干扰情形相同,敏感频段也与单频干扰情形相同;干扰信号同样被线性放大,虚警目标电平的强度由b1A1E1与b1A2E2决定,当双频干扰信号中任一分量增强时,由该分量产生的虚警目标电平均线性升高。
随着双频干扰信号增强,电路非线性失真不可忽略,可用幂级数展开法进行分析。考虑三阶非线性失真,将精确至三阶项的幂级数展开式作为系统传递函数[14],即
(4)
其中,bi(i=0,1,2,…)是与电路特性有关的非线性系数。结合式(1)可知,当系统受到双频干扰时,系统输出可由uo(t)uL(t)计算,其结果包含双频干扰基波分量,即
(5)
进而得到两干扰分量的增益分别为
(6)
其中,K(i,2)(i=1,2)表示双频干扰下,干扰分量i的增益。
若仅考虑至三阶非线性失真,则由式(6)可知,由于非线性系数a3<0,双频干扰中各分量的增益被有用信号、该分量自身以及其他干扰分量压制,压制效果与各信号有效电平的平方有关;任一干扰分量的增强均会导致各分量增益的降低。若非线性失真程度继续增加,则虚警电平的变化规律需要通过试验来分析。
1.2 虚警目标波形特征与位置规律
为便于说明,采用复信号的形式进行相关讨论。结合式(1)可知,频率步进连续波雷达在双频电磁辐射干扰下,接收信号[15-16]可表示为

A2E2e-j(2πf2t+φ2)
(7)
(8)
其中,A(s,i)、E(s,i)、ηi分别为有用信号第i个子周期信号的选择系数、场强幅值、初相位,fin为起始发射频率,Δf为频率步进阶梯,N为子周期数,R为目标距离,c为光速,2R/c=τ表示目标回波的时延。
本振信号可表示为

(9)
将式(7)与式(9)混频,并假设雷达采样时刻t=Δt+iTr(i=0,1,…,N-1),可得采样后的信号为
uif(i)=u(if,s)(i)+u(if,1)(i)+u(if,2)(i)
(10)
有用信号与双频干扰信号分量分别为
(11)
u(if,1)(i)=A1E1e-j(2πfinΔt-φ1-2πf1Δt)·
e-j2π(finTr+ΔfΔt-f1Tr)ie-j2πΔfTri2e-jηi
(12)
u(if,2)(i)=A2E2e-j(2πfinΔt-φ2-2πf2Δt)·
e-j2π(finTr+ΔfΔt-f2Tr)ie-j2πΔfTri2e-jηi
(13)
在后续信号处理中,需对式(10)进行快速傅里叶逆变换(inverse fast Fourier transform,IFFT)并求模,即
|H(k)|=|FIFFT[uif(i)]|=|FIFFT[u(if,s)(i)]|+|FIFFT[u(if,1)(i)]|+|FIFFT[u(if,2)(i)]|
(14)
首先对真实目标的成像过程,即对式(10)u(if,s)(i)进行分析。结合式(11)可知,u(if,s)(i)中第一个指数项e-j4πfinR/c为常数,而第二个指数项e-j4πΔfRi/c可以看作时间点为2R/c、频率呈线性变化的频域信号[15],令
ys(i)=e-j2πil/N
(15)
其中,l=FRound(2RNΔf/c),i=0,1,…,N-1,FRound(x)为四舍五入取整运算。
若忽略u(if,s)(i)的幅度信息A(s,i)E(s,i),则对其进行IFFT运算并求模可得
(16)
其中,当k=l时,|FIFFT[ys(i)]|达到最大,由门限判决可得到k值[15]。结合l=FRound(2RNΔf/c)得到真实目标的位置R,即
(17)
下面分析双频虚警目标的成像特征。以双频干扰信号中分量1形成的虚警目标1为例,即对式(10)中u(if,1)(i)进行分析,结合式(12)可知:
1)第一个指数项e-j(2πfinΔt-φ1-2πf1Δt)为常数,对距离像的产生没有影响。
2)第二个指数项e-j2π(finTr+ΔfΔt-f1Tr)i含有变量i,为一次相位,可看作时间点为1、频率呈线性变化的频域信号,结合前文对于真实目标成像过程的讨论可知,该项经过IFFT等处理,会产生位置固定的虚警目标。
3)第三个指数项e-j2πΔfTri2中含有变量i2,为二次相位,由本振信号(发射信号)产生,会使得干扰信号能量发散,进而导致由第二个指数项产生的虚警目标波形展宽,降低其峰值,增高旁瓣电平[17-18]。
4)第四个指数项e-jηi中ηi为本振信号(发射信号)各子周期的初相位,其不同取值对第二个指数项产生的虚警目标的影响也不同。若在不同探测周期内,ηi随i的变化具备特定规律,则会导致该虚警目标在原有位置上产生固定距离的移动;若ηi随机变化,则每次探测后该虚警目标位置随机。
下面对虚警目标1的位置表达式进行推导。由于式(12)中第四个指数项对虚警目标位置的影响需结合具体装备特性分析,故首先忽略其影响,仅由其第二个指数项推导虚警目标位置,令
y1(i)=e-j2πim/N
(18)
其中,m=FRound[N(finTr+ΔfΔt-f1Tr)],i=0,1,…,N-1。同样忽略u(if,1)(i)的幅度信息A1E1,按照如式(16)、式(17)相似的推导方式,由式(18)可得到虚警目标的中心位置为
(19)
若考虑初相位序列ηi的影响,假定该序列使得R10产生数值为R(ηi)的位移,此时虚警目标位置可以表示为
(20)
需要注意的是,式(20)在实际应用中须考虑距离折叠等因素[15]。假设频率步进连续波雷达满足紧约束条件,发射信号子周期对应的不模糊距离为
rτ=cTr/2
(21)
则虚警目标实际出现位置为
(22)
其中,FFloor(x)为向下取整函数。
同理,干扰分量2形成的虚警目标实际出现的位置为
(23)
其中
R′2=R20+R(ηi)
(24)
由以上分析可知,双频电磁辐射进入雷达接收机与本振混频后,会在后端信号处理电路中产生虚警干扰,导致出现两个虚警目标。由于本振信号产生的二次相位的影响,虚警目标波形会展宽。另外,若在不同探测周期内,发射信号各子周期初相位具备特定规律,则在雷达自身其他参数不变的情况下,虚警目标位置(距离)与干扰信号频率有关,可按照式(22)、式(23)计算。
联立式(20)~(24)可知,双频电磁辐射直接形成的两个虚警目标的距离差为
ΔR=R2-R1
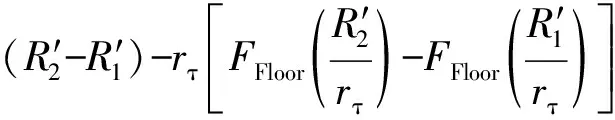
(25)
其中,ΔR的符号可反映两个虚警目标相对位置关系。
(26)
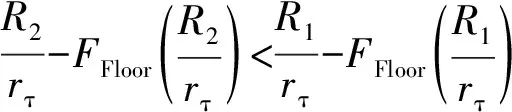
(27)
由以上可知,若不考虑互调因素,由带内双频电磁辐射产生的两个虚警目标波形特征与单频情形相同[12]。若频率步进连续波雷达满足紧约束条件,则两个虚警目标距离差存在两种情况,可分别按照式(26)、式(27)计算。
2 双频电磁辐射虚警干扰效应试验
2.1 试验布置
搭建雷达双频连续波电磁辐射效应试验平台,如图1所示。其中,干扰端的设置为:使用两台信号发生器产生双频连续波作为干扰信号,与宽带微波功率放大器连接,控制干扰端的工作状态(辐射控制),其注入功率由频谱仪通过定向耦合器实时监测;辐射天线将双频干扰信号辐射至外部环境,同时为了简化试验布置,其又预设为受试雷达探测目标。测试端的设置为:调整受试雷达天线与辐射天线,使两者主瓣相对、极化相同,确保受试雷达处于易受扰状态。为避免受试雷达发射信号以及外壳反射影响场强测量结果,试验过程中结合位置替换法与线性外推、内插法获得环境场强[19-20]。
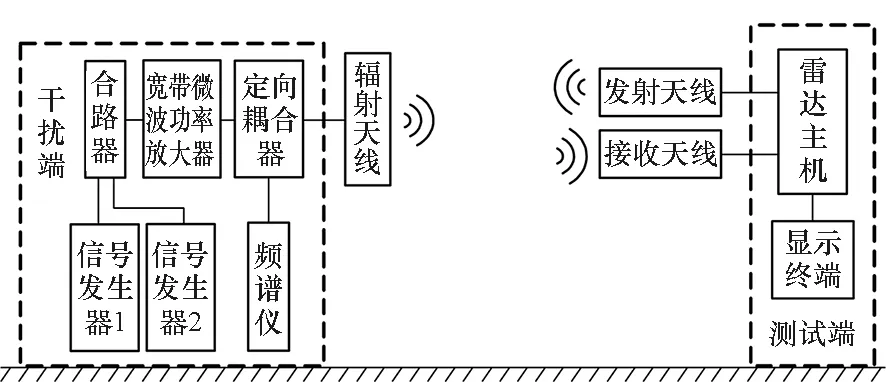
图1 雷达双频连续波电磁辐射效应试验平台Fig.1 Radar dual frequency continuous electromagnetic radiation effect test platform
受试雷达为某型Ku波段频率步进连续波雷达,工作频率设计为f0±100 MHz(f0为中心频率),可实现静目标测距,并产生目标回波的一维距离像,不同目标的强弱由归一化电平来表示,如图2所示。归一化电平所反映的实质是各位置电平与峰值电平的差值,而在研究过程中应以不同位置的绝对电平为对象。
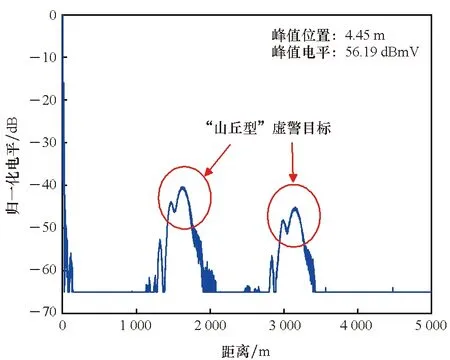
图2 双频干扰形成的虚警目标示意图Fig.2 Schematic diagram of false alarm target formed by dual frequency interference
2.2 双频虚警目标特征测试
首先观察受试雷达在双频电磁辐射作用下出现的虚警目标波形特征。设定信号发生器1、2分别输出辐射频偏为Δf1=0 Hz、Δf2=20 MHz(辐射频偏Δfi=fi-f0)的干扰信号,使用受试雷达对预设探测目标进行探测,某次测试后得到的一维距离像如图2所示。在图2中,可以很明显地看到,受试雷达一维距离像中出现了两个虚警目标,其波形呈“山丘”状,在距离轴上占据了相当的宽度,与前述理论分析内容相符。
下面继续通过试验对虚警目标出现位置的规律进行探究。选定双频干扰频偏后,设定两干扰分量场强相差6 dB以上,使得两个虚警目标电平存在明显差距,便于分辨虚警目标来源;连续进行20次探测,记录两个非互调虚警目标实际出现的位置R1与R2,计算其距离差ΔR,结果如表1所示。

表1 虚警目标位置及其距离差(Δf1=0.02 kHz,Δf2=3.92 kHz)Tab.1 Positions and range difference of false alarm targets(Δf1=0.02 kHz, Δf2=3.92 kHz)
在表1中,对于任一虚警目标,可认为其出现位置是随机的;两个虚警目标不一定同时出现在一维距离像中,但当两者同时出现时,两者距离差约为-2 900 m或4 600 m。
结合第1节理论分析结果对该现象进行解释。任一虚警目标位置随机是由于受试雷达发射信号子周期的初相位随机,即式(12)、式(13)中ηi是随机的。在第2.1节中,给出了受试雷达发射信号的各项参数,将其代入式(26)、式(27)中,可得到两个虚警目标距离差为-2 925 m或4 575 m,该数值与试验结果相符;另外,结合式(21)可知,发射信号子周期对应的不模糊距离为rτ=cTr/2=7 500 m,距离像最大不模糊距离为rI=c/2Δf=15 000 m,满足紧约束条件[16],而受试雷达仅能显示5 000 m范围内的目标,若虚警目标位置超出显示范围则无法被观察到,与试验结果相符。
2.3 单个干扰分量变化对虚警电平的影响
通过开展效应试验,改变双频连续波电磁辐射中任一分量的强度,探究虚警电平该分量强度变化的规律。试验布置与图1相同,选择一组带内干扰频率进行测试。设定信号发生器1输出固定功率、辐射频偏为Δf1=-20 MHz的干扰信号;在此基础上设置信号发生器2输出辐射频偏为Δf2=40 MHz的干扰信号,调整其输出功率,使得虚警目标归一化电平平稳变化。得到虚警目标1、2电平随干扰分量2场强的变化规律,如图3所示。

(a) 虚警目标1(a) False alarm target 1
图3中,不论干扰分量1强弱,随干扰分量2场强的增加,虚警目标1、2电平的变化趋势均可分为三个阶段,且该趋势与系统的非线性失真程度密切相关。
1)干扰分量2较弱时,受试雷达工作于线性状态,虚警目标1电平保持稳定,虚警目标2电平近似线性上升。
2)随着干扰分量2增强,系统非线性失真不可忽略,虚警目标1电平逐渐下降,虚警目标2电平增速放缓。
3)最终系统趋于饱和,虚警目标1电平近似线性降低,虚警目标2电平趋于稳定,且不论干扰分量1强弱,虚警目标2电平的稳定值几乎相同,这是由于干扰分量2强度远大于干扰分量1,几乎可以忽略后者的作用,这与理论分析相符。
2.4 两干扰分量同比例变化对虚警电平的影响
通过开展效应试验,同比例改变双频连续波电磁辐射两分量强度,探究虚警电平随总干扰场强变化的规律。试验设置如图1所示,设定信号发生器1、2分别输出辐射频偏为Δf1=-20 MHz、Δf2=40 MHz的双频干扰信号,使两干扰分量场强比E1/E2分别为保持3 dB、6 dB、9 dB;同比例调节信号发生器1、2输出功率,得到虚警目标1、2电平随干扰场强的变化规律,如图4所示。

(a) 虚警目标1(a) False alarm target 1
图4中,在不同场强比的双频电磁辐射干扰下,虚警目标1、2电平随干扰场强的变化趋势较为相似,该趋势同样与系统非线性失真程度紧密相关,可分为三个阶段:初期近似线性上升,而后增幅趋缓,最终虚警电平保持稳定,这与理论分析相符。
3 结论
本文以频率步进连续波雷达受到双频电磁辐射干扰为背景,结合理论分析与效应试验,在不考虑互调干扰的影响时,研究了虚警干扰效应规律。具体的研究内容及结论如下:
1)分析了频率步进连续波雷达双频虚警目标特征。带内双频电磁辐射直接作用于受试雷达后,会产生两个“山丘型”虚警目标;每次探测后两者距离均产生变化,但两者的距离差具有明显规律,在雷达发射信号参数不变的情况下,距离差与双频干扰的频差有关,可按照推导出的公式计算。
2)研究了双频虚警目标电平变化规律。双频干扰中两干扰分量互相压制,某个干扰分量有效电平越高,其形成的虚警目标越难被另一干扰分量影响;若双频干扰信号中某干扰分量强度恒定,则随着另一个分量的增强,前者形成的虚警目标电平缓慢下降,最终降速基本恒定,而后者形成虚警目标电平逐渐升高,增速趋缓,直至电平恒定;若双频干扰信号两分量同比例变化,则随着干扰场强的提高,两个虚警目标电平的总体变化趋势基本一致,初期近似线性上升,而后增速趋缓,最终虚警电平基本保持平稳。
