说理辨析让空间观念发展留痕

陈春妮

图形的旋转是图形的变换形式之一，能从动态视角为学生观察图形、研究几何问题提供必要的经验，对发展学生的空间观念具有重要意义。《图形的旋转（二）》是建立在学生学习了平移、轴对称及旋转三要素的基础上的，主要目标是通过简單的平面图形的旋转，进一步认识旋转特征，会画简单图形旋转90°后的图形。如何引导学生把握旋转特征、发展空间观念呢？

一、从整体感知到要素刻画，在说理中聚焦旋转要素

空间观念的形成需要借助丰富的空间表象，课堂上教师每次呈现图形、明确旋转要求后，都让学生仔细观察图形、在头脑中想象图形旋转后的样子并画出来。这种观察、想象、画图是从整体感知的角度出发的，学生借助已有经验画图，旋转后的图像只是被“复制”进大脑，他们对图形运动的认识仅仅停留在表象层面。要使学生认识旋转的本质，就要引导学生将图形旋转的表象与旋转运动的要素建立充分联结。如何建立联结呢？笔者引导学生观察、说理，经历从建立表象到明晰本质的过程，使学生对旋转运动形成理性认知，发展学生的空间观念。

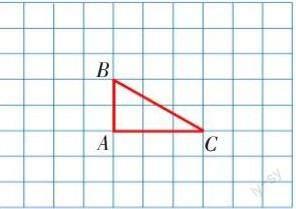
课堂上，笔者先出示下图并提问：“你能画出三角形ABC旋转90°后的图形吗？”

学生略显迟疑后回答：“我觉得不行，因为这里没有说明旋转中心和旋转方向，可以画出无数种情况。”笔者小结“说清楚旋转三要素才能准确画出旋转后的图形”后，出示“三角形ABC绕点A顺时针旋转90°”的补充条件，引导学生在头脑中想一想、转一转，然后动笔画一画，并思考：①我先画的什么？②我画对了吗？学生在方格纸上画图后，笔者引导学生结合旋转要求说一说画法。有的学生先画线段AC′，即把线段AC绕点A顺时针旋转90°后指向下方的线段画出来；再画线段AB′，即把线段AB绕点A顺时针旋转90°后变为横向的线段画出来；最后连接B′和C′。有的学生与此相反，先画线段AB′，再画线段AC′，最后连接B′和C′。笔者进一步引导：“大家都是先画这两条边吗？你们为什么要先画线段AB′或线段AC′，而不是先画线段B′C′呢？”这个关键问题引发了学生表达的欲望，他们纷纷举手说明理由，如“这两条边是直角边，直角边旋转90°容易画”，“这两条边都有一个端点A是旋转中心，容易观察，方便画”，“如果先画线段B′C′，不知道从哪里画起”等，并归纳出“先画与旋转中心相连的边会更方便”的结论。最后，笔者引导学生聚焦旋转中心、旋转方向、旋转角度，判断旋转后图形的每一条边是否符合旋转要求，描述正确的画法，并引导学生用三角板等进行验证。

在画图过程中，个别学生混淆了旋转与轴对称的图形运动方式。笔者在交流环节把这样的典型错例呈现出来，引导学生据此合作交流，分析错例出错的原因，指出具体的问题。这个过程中，学生观察图形运动的视角开始从整体形态向具体元素深入。

以上教学，通过让学生说一说先画的是什么、图形是否画对了等，引导学生关注图形中具体的点、线的刻画，围绕旋转中心、旋转方向、旋转角度观察和描述图形的画法和旋转后的特征，实现了从“经验性理解”向“结构化理解”的跨越。通过进一步说理，学生对旋转概念的认知更清晰了。

二、从“容错”到“化错”，在辨析中感悟旋转特征

不同学生空间观念发展的层次是不同的。面对学生学习过程中的错误理解，教师的正确选择是把错误当作资源，充分利用学生课堂生成的学习资源，引导学生在交流中深入思考、在辨析中发现问题、在“化错”中不断逼近旋转运动的本质，感悟旋转的特征。

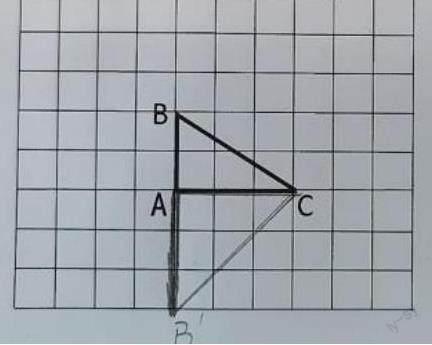
课堂上，笔者先出示学生A画的三角形ABC绕点A顺时针旋转90°的作品（如下图），让学生观察，并说一说该作品的问题。

一名学生提出“这幅图中，三角形ABC旋转后形状变了，不是原来的三角形了”，另一名学生从三角形的特征出发，进一步说明旋转后图形的高增加了，面积变大了。听了大家的意见，学生A发现了自己所画作品出现的问题，明确了旋转后的三角形应该和原来的三角形形状、大小都一样，如果旋转后的图形变形了，那一定是出错了。笔者及时肯定了学生善于观察、反思的学习习惯后，引导学生继续观察并思考“旋转后的图形和原来的图形哪里不一样”。学生在交流中明晰：与原来的图形相比，旋转后图形的位置和方向发生了变化。

以上“化错”过程让学生自觉聚焦旋转后图形的特征，并在观察、比较和辨析中主动发现并描述了图形在旋转前后的“变”与“不变”，进一步明晰了图形旋转的特征。

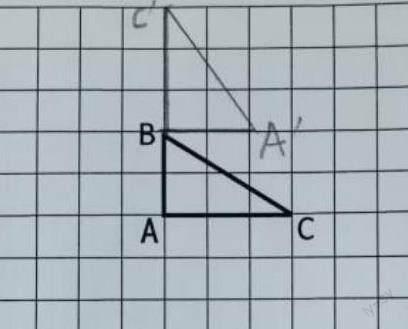
当改变三角形的旋转要求（三角形ABC绕点B逆时针旋转90°）后，笔者发现了学生画图中出现的共性问题，如学生B的作品（如右图）。该作品出错的原因是学生空间想象力不足，且受到了前一次画图经验的干扰。

课堂上，笔者呈现了学生B的作品，让他说一说自己画图的过程。学生B围绕旋转三要素介绍了自己的画法后，一名学生质疑：“三角形旋转90°后，点C′应该在点A′的上方，现在点C′为什么在点A′的斜上方？”这个问题指向性不强，不足以让学生B发现自己作品出现的问题。于是，笔者启发其他学生谈一谈该作品出错的原因。经过思考，一名学生说：“这幅作品虽然画的也是直角三角形，但是直角不应该在∠B处，而应该在∠A处”。另一名学生补充道：“原图形中线段BC是斜边，而这幅作品中线段BC′变成了直角边，这样不对”。两名学生的说法让学生B恍然大悟：“我所画的旋转中心不是三角形的直角所在的顶点，我知道该怎么改了。”学生B很快对自己的作品进行了修改。有类似错误的学生都明白了出错的原因，对图形的旋转形成了正确的认知，并掌握了旋转图形的正确画法。

随后，笔者让学生围绕以上纠错过程说一说自己的收获。学生认为：画旋转后的图形时，不能只看所画图形的形状、大小有没有改变，还要对比旋转后图形的各个顶点与原来图形的各个顶点是否对应，也就是要看图形的基本特征有没有改变。还有的学生给出建议：“从与旋转中心相连的边开始画更方便，因为线段AB和线段AC都与旋转中心点A相连，所以应该先画线段AB（或AC）旋转后的线段AB′（或AC′），再连接B′和C′；用三角板上的直角比着画，也能辅助我们观察图形的基本特征，这样不容易出错。”

以上“化错”过程中，教师引导学生通过对比观察错误作品，聚焦图形的基本特征，又通过深入辨析图形旋转后的“变”与“不变”，进一步内化图形旋转的特征，增强空间观念。

（作者单位：宜都市实验小学教育集团）

责任编辑 刘佳