SOLO分类评价理论在物理课堂教学中的应用
2023-06-10沈文炳

SOLO分类评价理论为确定复杂的学习过程和层次提供了通用框架。它可以指导教师准确把握学生的学前思维层次,完善教学目标设计,优化课堂教学和作业设计,从而提升学生的思维层次。湖北省鄂南高级中学沈文炳老师所在的课题组依托“基于SOLO理论的高中物理教材习题的实践研究”课题,对在物理课堂教学及评价中应用SOLO分类评价理论的策略进行了探究。
《普通高中物理课程标准(2017年版)》提出物理学科核心素养主要包括“物理观念”“科学思维”“科学探究”和“科学态度与责任”。实际教学中,如何根据课程标准制定教学目标、设计教学过程及教学评价,提高学生的物理核心素养水平层级呢?本研究尝试把SOLO分类评价理论应用到物理教学的各个环节,以促进学生深度学习,有效提高课堂教学效率。
一、明晰基于SOLO分类层级的核心素养表现
SOLO分类评价理论把思维分为五个层次:前结构、单点结构、多点结构、关联结构和拓展抽象结构。高中物理学科核心素养水平分为五个等级。其中,一级、二级为合格考试所要求的等级,分别处于单点结构和多点结构思维能力层次;三级、四级主要为学业水平能力测试所要求的层次,处于弱关联结构和强关联结构思维能力层次;第五级水平主要为高校自主招生命题所要求的水平,主要对应拓展抽象结构思维能力层次。
基于SOLO分类评价理论的物理学科核心素养水平划分,为教师进行有梯度的教学设计提供了有力的支持。以基于SOLO分类层级的科学探究素养表现为例,思维能力处于前结构水平的学生几乎不能理解现象中的物理模型,不能做出有意义的解释;处于单点结构(水平1)的学生有问题意识,能使用简单器材收集数据,能初步整理数据,有交流意识;处于多点结构(水平2)的学生能提出问题,能根据方案用基本器材获得数据,能整理数据,得到初步结论,能写简单的报告;处于弱关联结构(水平3)的学生能提出可探究的问题,能在教师的帮助下制订方案,用基本器材获得数据,能分析数据、发现特点、形成结论并做出解释,能写实验报告,能用学科术语和图表展开交流;处于强关联结构(水平4)的学生能提出准确的问题,能自主制订方案、选用器材并获得数据,能分析数据、发现规律、形成结论并做出合理解释,能写完整的实验报告;处于拓展抽象结构(水平5)的学生能多角度提问,创新设计方案,灵活选用器材获得数据,运用多种方法分析数据、发现规律,形成合理结论并做出科学解释,能写出完整的实验报告,并交流反思。
二、优化课堂教学设计过程
基于SOLO分类评价理论的物理课堂教学设计应基于教学内容和学情分析,统筹考虑学习情境创设、信息资源嵌入、学习支架设计等。下面以《力的合成》教学设计为例做具体说明。
1.教学内容和学情分析
SOLO分类评价理论可用于分析掌握教学内容所需的思维能力层次,以及教学内容对学生的认知负荷。通过分析,教师能确定具有思维能力层次结构的教学目标、教学重难点以及学生的最近发展区,使学习过程由直观逐渐过渡到抽象,体现螺旋式上升的特点。
《力的合成》的教学涉及等效思想、弹簧读数、实验操作和数据处理等核心知识。其中的等效思想要从单点结构向多点结构发展。学生已经知道多个电阻串(并)联的总电阻、平均速度等标量等效情境,而分力与合力的等效属于矢量等效,涉及方向这个要素,思维能力属于多点结构。弹簧读数要从前结构向多点结构发展。初中阶段对学生读取弹簧秤数据的要求不高,学生的弹簧秤读数能力处于前结构;高中阶段对学生读取仪器数据的能力要求属于多点结构,学生在使用弹簧秤前要校对零刻度,读数时眼睛要正视,也可适当估读。实验操作要从单点结构向关联结构发展。学生在实验时需要在木板上固定白纸和橡皮条,在橡皮条的另一端固定小圆环,在圆环上固定两根细绳套。这些操作看似简单,实际需要学生具有较强的动手能力和协调能力。数据处理要从前结构向关联结构发展。由于学生初次接触矢量的运算,加上实验操作的误差,学生很难想到分力和合力之间构成一个平行四边形。
2.学习情境创设
情境的实际化和情境的变易是引导学生认识问题本质、提升思维层次、发展创造性思维的有效方法。教学时,教师可以通过创设悬疑情境激发学生探究的兴趣,通过解释悬疑情境验证平行四边形定则。
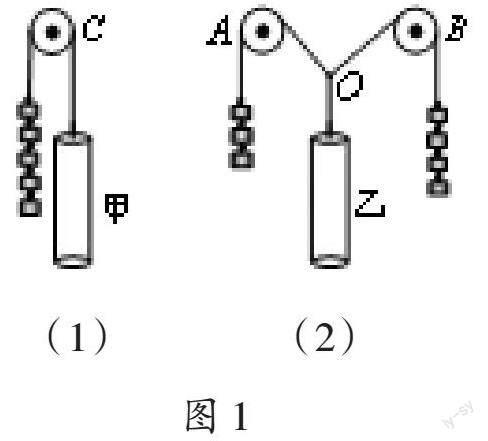
如图1所示,在黑板右上角悬挂被遮挡的钩码组甲和乙,甲用定滑轮C悬挂,乙用定滑轮A、B悬挂。
教师请学生猜一猜图1(1)中被遮挡的钩码组甲中有多少个钩码、图1(2)中被遮挡的钩码组乙中有多少个钩码,并讨论确定乙的钩码个数的具体办法。学生探究后,教师为学生示范,进一步验证平行四边形定则。
3.信息资源嵌入
在解决问题的过程中,教师应该及时嵌入结构化的信息资源,为学生搭建“脚手架”,帮助学生实现思维能力层次的逐级上升。
教学中,教师可以通过提供力的平行四边形定则的发展过程的相关史料,如从亚里士多德的三个力构成矩形的平行四边形定则、斯蒂文(荷兰)的成直角的两个力的三角形定则(单点结构)到牛顿的物体同时受两个力作用时将沿平行四边形的对角线运动的推断(多点结构),再到瓦里翁(法国)的力、速度的合成的平行四边形定则(关联结构),直至潘索(法国)的平行四边形定则的数学证明(拓展抽象结构),让学生由浅入深地认识力的平行四边形定则。
4.学习支架设计
教学中,教师可以通过问题串为学生提供合作学习的支架,促使学生在协作中展开科学探究,实现思维能力层次从前结构、单点结构向多点结構、关联结构发展。在学生经历使用弹簧秤、读取弹簧秤读数、记录力的方向及作用等实验探究过程中,教师提供了5个问题支架。问题1(单点结构),请大家观察弹簧秤的指针是否指在零刻度?如果不是,该怎样调整?问题2(多点结构),请大家观察弹簧秤的最小刻度是多少?思考读数的时候该怎样估读?问题3(弱关联结构),怎样理解用两个弹簧秤和一个弹簧秤拉橡皮条的效果相同?问题4(弱关联结构),三名学生一组,如何分工?问题5(强关联结构),如何记录力的大小和方向?教师有效的问题引导,让学生有序推进实验,得出准确的实验结论,并学会有意识地分工与合作。
三、监控和评价教学效果
知识的建构过程包含知识探究、学习调控及知识应用等高层次智力活动。为有效监控和评价教学效果,教师可以将SOLO分类评价理论与过程性评价相结合。具体的操作要点如下。
一是实时调控学生的学习过程。教师对学生的学习过程进行观察,可以了解学生的学习水平,及时改进教学。学生也可以根据教师对其学习水平的评价,发现自己在学习中的不足,并在之后的学习中明确方向和目标。
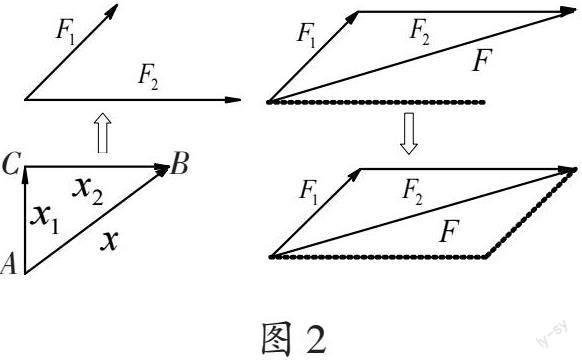
寻找三个力的几何关系是本课的教学难点。教师引导学生回顾教材问题情境“一位学生从操场中心A点出发,向北走了40m,到达C点,然后又向东走了30m,到达B点”,并依据思维能力层次进行如图2所示的分析合力和分力关系的思维过程:第一步为多点结构,用有向线段x1、x2和x表明他第一次、第二次的位移和两次行走的合位移;第二步为弱关联结构,明确三个位移的大小分别为40m、30m和50m;第三步为强关联结构,通过实例总结出矢量相加的方法,即两个分力F1和F2与合力F构成一个三角形;最后一步为拓展抽象,观察三个力的几何关系,发现力的合成规律,即平行四边形定则。
二是评价学生提出问题的能力。利用SOLO分类评价理论,根据学生提出的问题判断他所处的思维水平、思维的复杂程度和发展阶段并给予合理的评价,不仅可以考查学生对概念等知识的掌握程度,还可以外显学生的思维过程。这样的评价可以有效弥补传统教学评价中根据问题的答案评价的片面性和不足,使教师更好地了解学生,及时给予学生教学干预。
例如,学生对“分析物体受力个数时,是否需要同时计算分力和合力的个数”有疑问,教师可以判断学生对分力和合力关系的理解处于多点结构,需要通过实例分析把学生的思维提升到关联结构。于是,教师设计了“两名学生提一桶水”的学习情境,引导学生进行如下分析:首先从施力物体角度分析,水桶只有两名学生和地球三个施力物体,水桶只受三个力,没有所谓的合力的施力物体存在;其次从力的平衡角度分析,水桶受到的三个力的合力为零,如果还有第四个力,水桶就无法平衡,与问题矛盾;最后从等效角度分析,两名学生提水的两个分力和它们的合力之间是等效替代关系,不能重复计算。
三是通过SOLO试题检测教学效果。SOLO试题就是运用SOLO分类法的基本思想对学生的开放式反应做出相应成绩评定的测量工具。教学中,教师可以将原始的开放性问题改编成符合SOLO分类评价的4个层次(单点结构、多点结构、关联结构和拓展抽象结构)的4个小问题,以检测课堂教学效果和学生的思维能力层次,进一步反思和改进课堂教学。
如在复习过程中,教师通过编制SOLO试题了解学生掌握“探究光的反射规律”实验操作的情况。试题如下:
“探究光的反射规律”的实验装置如图3(1)所示。平面镜放在水平桌面上,标有刻度(图中未画出)的白色纸板ABCD能绕垂直于CD的ON轴翻转,在纸板上安装一支可在纸板平面内自由移动的激光笔。
(1)实验前,应将纸板_________________放置在平面镜上;
(2)实验中,为了使光线能在纸板上显示出来,他们应该______________ ;
A.让光束垂直纸板射到O点
B.让光束贴着纸板射到O点
(3)纸板ENF是用两块纸板连接起来的。如图3(2)所示,把纸板NOF向后折,光沿EO入射在纸板NOF上,不能看到反射光线。这说明在光的反射现象中,______________ ;
(4)若将纸板倾斜(即纸板与平面镜不垂直),如图3(3)所示,使反射光线从镜面O点反射后仍贴着纸板沿OA方向射出,则入射光线在 ______________。
試题主要考查学生的实验操作能力。第(1)题为单点结构,考查学生的仪器组装能力;第(2)题为多点结构,考查本实验的基本操作步骤;第(3)题为关联结构,考查学生是否了解相应实验操作步骤对应的实验结论;第(4)题为拓展抽象结构,考查学生对反射规律的灵活应用能力。
(作者单位:湖北省鄂南高级中学)
