基于连续损伤力学的剩余疲劳寿命随机预测

刘世洲,何声馨,张二亮

(郑州大学 机械与动力工程学院, 郑州 450001)

0 引言

疲劳破坏是材料在循环载荷作用下损伤累积、性能退化,最终导致断裂的一种失效形式,对构件的结构完整性和可靠性构成严重威胁。因此,预测在变幅加载下的剩余疲劳寿命是设计和维护阶段抗疲劳措施的主要关注点[1]。然而,构件在服役工况下的疲劳过程通常具有不确定性,主要来自材料特性和外部载荷的随机性,使得变幅加载下剩余疲劳寿命预测变得更加复杂[2]。为了解决疲劳过程中材料疲劳性能的固有可变性给疲劳寿命预测带来的潜在不确定性问题,Gao等[3]将不同应力水平下的疲劳寿命视为随机变量,借助基于统计分布函数的S-N曲线和可靠性分析理论,来量化疲劳寿命的概率特征;Zheng等[4]利用不同可靠度下S-N曲线,预测45钢缺口件的疲劳寿命概率分布。

除了材料特性的随机性外,考虑外部加载的随机性也是可靠的疲劳寿命预测的关键。由于线性损伤累积准则往往忽略加载顺序、载荷交互作用等外部加载的影响[5],为了避免其固有的缺点和局限性,许多非线性损伤累积模型被提出,Xia等[6]结合等损伤曲线的概念,提出一种基于韧性损耗的损伤累积模型,用于两级加载下疲劳寿命的预测;由于CDM模型可以考虑外部加载的影响,Zhang等[7]提出一种结合连续损伤力学(CDM)和裂纹扩展速率方程修正的损伤累积模型,以裂纹尺寸作为损伤指标来估算剩余疲劳寿命;Leonetti等[8]基于平均应力修正的随机疲劳极限模型,结合相对线性损伤准则,提出一种变幅载荷下焊接细部的概率疲劳寿命预测模型。

确定性疲劳损伤累积模型不能考虑疲劳寿命的分散性,使用非侵入方法构建随机模型,会由于模型参数众多导致模型复杂度和计算成本急剧增加。基于方差分析的Sobol方法是一种全局敏感性分析(GSA)方法,它能用于显著性模型参数的选取和模型简化等。Du等[9]将基于Sobol方法的全局敏感性分析应用于参数服从正态分布的基于循环塑性的损伤累积模型,研究输入参数的变化对疲劳寿命的影响。

本文提出一种简单实用的方法来考虑两级加载下剩余疲劳寿命的不确定性。首先,通过构建P-S-N曲线,获得材料特定参数的概率分布;其次,采用非侵入蒙特卡洛模拟方法,基于连续损伤力学的剩余疲劳寿命预测模型,实现不确定度的传递和量化,并借助统计推断获得不同加载顺序下剩余疲劳寿命的概率分布;再其次,引入基于Sobol方法的全局敏感性分析,筛选对剩余疲劳寿命有显著影响的模型参数;然后,利用K-L散度量化预测与实验的剩余疲劳寿命概率分布之间的差异,评价疲劳寿命预测精度;最后,借助热轧16Mn合金钢的疲劳寿命实验数据对所提方法进行验证。

1 剩余疲劳寿命预测

1.1 CDM模型

材料的疲劳行为可以看作是一个损伤累积,直至疲劳失效的连续过程,在本文研究案例中,只考虑对称循环应力载荷(应力比R=-1)和单轴应力问题,由Chaboche[10]提出的疲劳损伤微分方程为:

(1)

式中:D为损伤变量,D=0代表无损伤状态,D=1代表疲劳失效状态,随着疲劳损伤不断累积,D逐渐趋近于1;σa为循环应力幅,n是给定σa下的循环次数;β和M0取决于材料的参数;指数α是σa的函数,指数α选用如下函数表达式[11]:

(2)

式中:a和H为由实验确定的参数;σf为材料疲劳极限;σu为材料抗拉强度;〈〉为麦考利括号符,x>0时,〈x〉=x;x<0时,〈x〉=0。

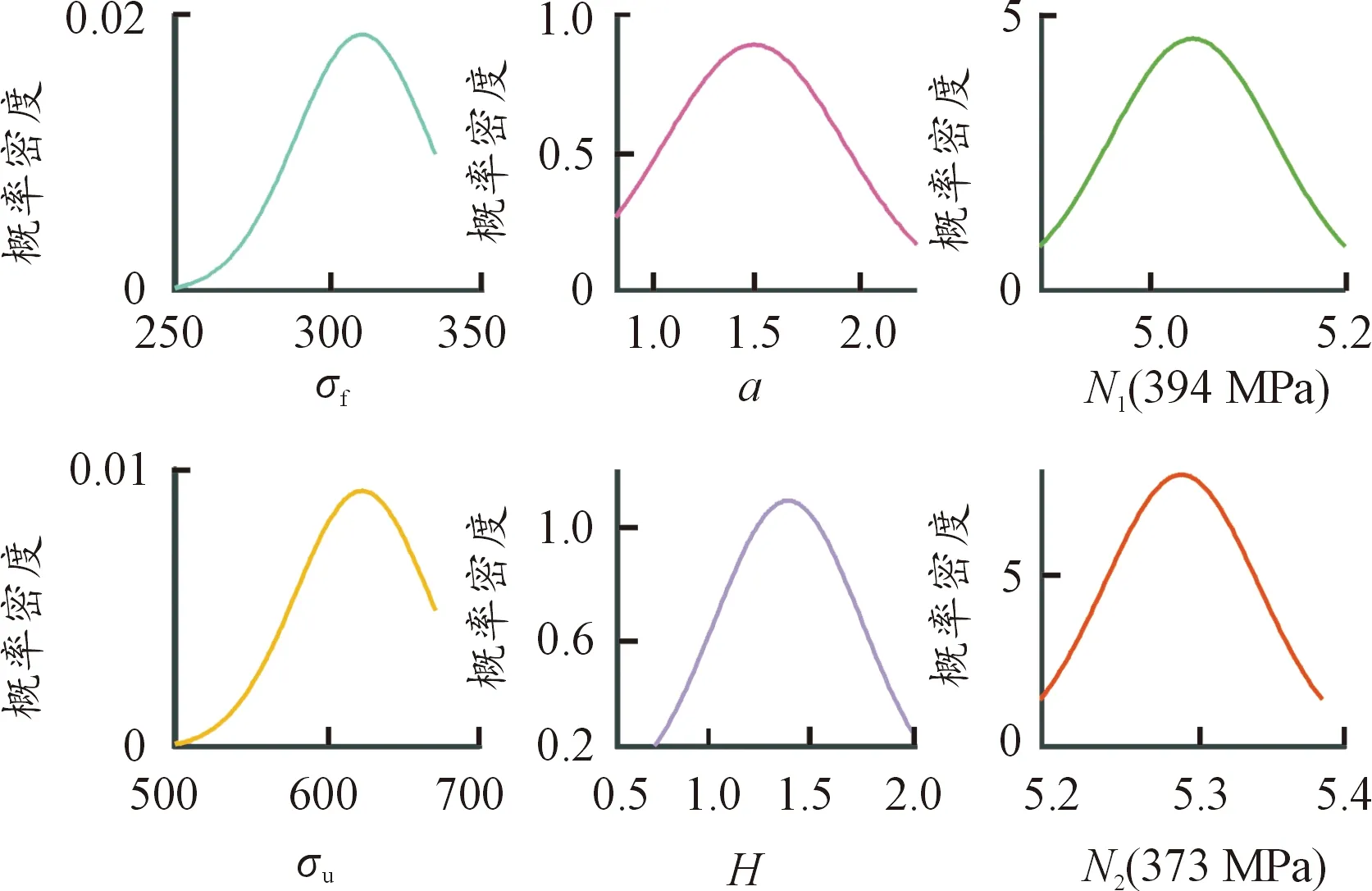
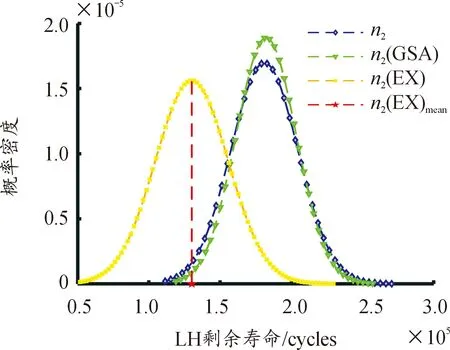
在疲劳失效前的一般瞬时,即D<1,n

(3)

(4)

式中:N1和N2分别为在σa1和σa2下的疲劳寿命;α1和α2分别为σa1和σa2的函数。

1.2 P-S-N曲线构造

本文假设应力水平Si下每组对数疲劳寿命服从正态分布[13],给定可靠度P下的对数疲劳寿命lgNp有:

lgNp=lgN0.5-upσ

(5)

式中:lgN0.5为对数疲劳寿命的均值;σ为对数疲劳寿命的标准偏差;up为标准正态偏量。

本文选用三参数幂函数方程[13]来描述应力水平与疲劳寿命之间的关系,取对数后可转换为:

lgNp=A+Blg(Si-S0)

(6)

式中:A和B为待拟合参数;S0为拟合疲劳极限。通过最大化线性拟合相关系数,利用割线法[13]迭代求S0的最优解,从而确定三参数A、B和S0。

1.3 全局敏感性分析

本文将全局敏感性分析应用于研究剩余疲劳寿命的不确定性如何归因于CDM模型参数的变化,从而减少模型不确定性输入,有助于模型的校准、验证和简化等[14]。

Sobol敏感性分析是一种基于方差分解的全局敏感性分析方法,其物理意义明确、不依赖于特定的模型假设、适用于非线性模型,被广泛应用于各个领域[15]。

设基于CDM模型的剩余疲劳寿命预测方程为n2=f(σf,σu,a,H,N1,N2),输入变量包含6个模型参数。首先,将不同可靠度下的模型参数作为原数据,基于拉丁超立方采样进行2次相互独立的采样,在各输入变量的取值范围内,按其服从的概率分布扩充至T组数据,分别获得矩阵M1和重采样矩阵M2;然后,将采样得到的模型参数代入预测方程中,计算相应的n2;最后,基于Sobol提出的蒙特卡洛估计法[15],求出各模型参数对n2的一阶敏感性指数SEi:

(7)

1.4 剩余疲劳寿命的概率分布

为了模拟两级加载下n2的不确定性,首先,考虑材料特性的随机性,构建P-S-N曲线获得模型参数的概率分布;然后,基于CDM的剩余疲劳寿命预测方程传递模型参数的不确定性;最后,通过统计推断得到n2的概率分布。

1) 在模型参数的取值范围内,基于拉丁超立方采样,从其服从的概率分布中随机抽取1 000组参数,代入基于CDM的剩余疲劳寿命预测方程,即可获得n2样本集。

2) 经GSA筛选敏感性参数后,对n2影响显著的参数,基于拉丁超立方采样,从其服从的概率分布中随机抽取1 000组参数,对n2影响微弱的参数,将其设定为对应可靠度为50%的常数,代入基于CDM的剩余疲劳寿命预测方程,即可获得经GSA的n2样本集。

3) 本文选用正态分布来描述n2、经GSA的n2和实验的n2的分布特征,根据已获得的n2、经GSA的n2和实验的n2的有限样本集,进行合理的统计推断,从而获得三者总体的概率分布。

1.5 K-L散度

本文选用K-L散度作为评估指标,来衡量预测与实验剩余疲劳寿命概率分布之间的相似性[16],将剩余疲劳寿命视作连续随机变量x,2个连续的概率分布W和Q之间的K-L散度定义为:

(8)

式中:W为预测的剩余疲劳寿命概率分布;Q为实验的剩余疲劳寿命概率分布;w(x)和q(x)分别为W和Q的概率密度函数。K-L散度越大,表示W和Q差异越大;K-L散度越小,表示W和Q越相似。

2 实验验证

2.1 实验数据

本文选择文献[17]中疲劳试验数据,试验材料为热轧16Mn合金钢,光滑试样的材料成分、力学性能和几何形状参见文献[17]。

恒幅加载下疲劳试验数据包含3种不同应力水平,3种应力水平分别为394、373、344 MPa,每个应力水平Si下选用15个光滑试样进行旋转弯曲疲劳试验,得到相应的疲劳寿命数据点。恒幅加载下的疲劳试验数据及统计特性[18]被用来拟合P-S-N曲线。

两级加载下疲劳试验数据包含2组加载序列,2组加载序列分别为373～394 MPa和394～373 MPa,2组加载序列的第一级循环比n1/N1分别为0.32和0.23,每组加载序列选用10个光滑试样进行疲劳试验。为了验证所提方法在不同加载水平和顺序下的适用性,将两级加载下的疲劳试验数据与预测结果进行对比,来分析两级加载对剩余疲劳寿命的影响。

2.2 P-S-N曲线

热轧16Mn合金钢的P-S-N曲线如图1所示。从图1可知,选择可靠度为5%和95%的S-N曲线作为边界,可以较好地反映实验疲劳寿命数据的分散范围;采用割线法迭代求解的S0与材料的疲劳极限真实值接近,故可选用S0替代σf,参考σu和σf之间关系的经验公式[19]计算σu。

图1 热轧16Mn合金钢的P-S-N曲线

对式(1)从D=0到D=1积分,获得给定σa下疲劳寿命的函数表达式[11],与传统S-N曲线相比,Dattoma等[11]证明该式可以较好地近似对数疲劳寿命和应力水平的关系。借助该函数表达式和恒幅加载下疲劳试验数据,结合蒙特卡罗方法和非线性最小二乘方法来估计a、β、H、M0,以误差平方和最小为准则,返回对数疲劳寿命残差的2-范数平方最小值。

假设σf、σu、a、H、N1、N2均服从正态分布,选择可靠度5%和95%分别作为初值和终值,以可靠度5%为间隔的步长,基于P-S-N曲线,并结合非线性最小二乘法,获得模型参数的概率分布。如图2所示,分别为模型参数的概率密度函数。

图2 模型参数的概率分布

2.3 基于GSA筛选敏感性参数

以0.3为阈值筛选敏感性参数[9],将对n2影响微弱的参数,即小于0.3时,将其固定为对应可靠度为50%的常数;对n2影响显著的参数,即大于0.3时,从其服从的概率分布中随机抽取。模型参数的一阶敏感性指数如表1所示。

2）渭北中、北部海拔较高、水肥条件较好和采用矮化中间砧（短枝型品种）与4 m×1.5～2 m行株距定植的苹果园，宜采用细长纺锤形。

表1 模型参数的一阶敏感性指数

由表1可知,在低高加载和高低加载下,σf、σu、a、H、N1影响较小,N2具有重要影响。这是由于第一级循环比较小,意味着第一级应力循环加载后,试样仍处在疲劳过程的前期,导致第二级应力循环加载在试样疲劳损伤累积中占主导地位;由于恒幅加载下疲劳寿命的分散性较大,与其他参数相比,波动范围的量级过大。

2.4 两级加载下剩余疲劳寿命预测

如图3—4所示,分别为在低高加载(LH)和高低加载(HL)下n2的概率密度函数,n2(GSA)和n2(EX)分别代表经GSA筛选敏感性参数后的和实验的剩余疲劳寿命,红色虚线代表n2(EX)的平均值。

图3 低高加载下剩余寿命的概率分布

图4 高低加载下剩余寿命的概率分布

由图3—4可见:

1) 在LH加载和HL加载下,n2和n2(EX)二者概率分布的整体形状相似,且分散范围接近,说明所提方法的不确定性预测是合理的。

2) 在LH加载和HL加载下,与n2相比,n2(GSA)的分散范围缩小,且与n2概率分布的整体形状相似且均值相差很小,说明采用GSA方法筛选敏感性参数是有效的。

2.5 K-L散度

选择K-L散度量化n2和n2(GSA)、n2(EX)的概率分布之间的差异,如表2所示。

表2 K-L散度

由表2可以看出:在LH加载和HL加载下K(n2‖n2(EX))与K(n2(GSA)‖n2(EX))较低、相差很小,K(n2(GSA)‖n2(EX))低于K(n2‖n2(EX))。说明预测的‖n2概率分布与实验的n2概率分布较匹配,且n2‖(GSA)概率分布与n2(EX)概率分布更接近,故可选用n2(GSA)的概率分布代替n2的概率分布,保留精度的同时,从而减少模型输入的不确定性,降低模型复杂度。

3 结论

针对由材料特性和外部加载的随机性引起剩余疲劳寿命不确定性的问题,提出一种基于连续损伤力学的剩余疲劳寿命随机预测方法,该方法通过利用P-S-N曲线构造模型参数概率分布考虑材料特性的随机性,并引入基于Sobol的全局敏感性分析方法筛选敏感性参数,保证预测精度的同时,降低了时间计算成本,结果表明:在两级加载下,对于不同加载顺序,预测与实验剩余疲劳寿命均值的相对误差均在高周疲劳可接受的相对误差范围内,验证了该方法的可行性。下一步将通过多级加载下的工程案例进一步验证本文方法的有效性。