基于穷举法的双电机插混动力耦合装置传动比优化

罗 勇,李小凡,陈国芳,刘增玥,邓 涛

(1.重庆理工大学 汽车零部件先进制造技术教育部重点实验室, 重庆 400054;2.中国汽车工程研究院股份有限公司 汽车噪声振动和安全技术国家重点实验室, 重庆 400054;3.重庆青山工业有限责任公司 技术中心软件开发所, 重庆 400054)

0 引言

随着能源危机和污染问题日益突出,对汽车行业的油耗和排放法规日趋严格。插电式混合动力汽车(plug-in hybrid vehicle,PHEV)具有纯电动汽车的多种优点,同时又避免了其存在的里程焦虑问题,具有广阔的市场前景。动力耦合装置作为PHEV关键部件,一直是相关研发的重点。PHEV在行驶过程中发动机输出的力矩都需经过动力耦合装置和主减速器的齿轮传动后再到车轮。动力耦合装置通常具有多个挡位,各挡速比的大小影响着动力源工作状态[1-2],从而影响到整车动力性和经济性[3-4],还会影响汽车行驶中换挡时产生冲击的大小[5-7]。

动力耦合装置本质上是一个变速装置,近年来国内外对动力耦合装置及汽车传动系速比优化开展了大量研究。王小军等[8]以原地起步加速时间为约束,3种工况油耗为目标函数,对两挡式变速器速比进行优化。宋强等[9]基于多目标粒子群优化算法,考虑静态换挡和动态换挡的同时进行传动系速比优化。尹安东等[10]使用非支配排序遗传算法,加入了精英策略,缩短了百公里加速时间和百公里油耗;赵韩等[11]利用优化前建立的换挡规律,以传动比为变量,提出一种既能解决配齿问题,又能让电机在高效区间工作传动比区间优化方法。Kihan Kwon等[12]针对双电机双速比的纯电动汽车,用神经网络算法和自适应采样算法优化了转矩分配和传动比,减小了双电机电动汽车的加速时间和能量消耗。Masoud Masih-Tehranid等[13]以带式推土机为研究对象,使用遗传算法,通过控制发动机转速和传动齿轮速比,有效地减少了发动机油耗和尾气排放。

速比优化的原理是在不同速比组合下对系统的动力性和经济性进行评价,进而选出性能最优的速比组合。当速比组合变化后,系统换挡规律将发生变化,需要在每一速比组合下重新计算换挡规律,这给整个优化计算增加了复杂度。现有的速比优化方法中对不同速比组合下换挡规律的变化较少考虑,或进行了不同程度的简化,一定程度上影响了计算精度。

针对上述问题,提出一种基于穷举法的动力耦合装置速比优化方法,让程序计算出所有速比组合的换挡规律,进而进行动力性和经济性评价,二者均衡后选出最优的速比组合。针对穷举法计算量大的问题,引入速比分配中的多重约束以减少计算量,并利用多线程方法设计程序以缩短计算时间。以该方法对一款搭载AMT的双电机动力耦合装置进行速比优化,获得其优化速比,并建立系统仿真模型对优化前后系统动力性和经济性进行对比分析。

1 双电机PHEV动力耦合装置结构

本文研究对象是基于机械式自动变速器(automated mechanical transmission,AMT)的P0、P3双电机插电式混合动力系统,其结构如图1所示。该结构中动力耦合装置类似于AMT,在动力耦合装置后端布置有功率较大的P3电机,可直接驱动车辆。在动力耦合装置前端通过离合器连接发动机,发动机前端布置P0电机,实现怠速起停、停车发电机及部分助力功能,弥补P3电机在这些功能上的不足。该系统传动效率高,在换挡及模式切换过程中,当离合器断开时,P3电机的扭矩仍可以传递到车轮,实现无动力中断换挡和模式切换,避免了普通AMT系统换挡过程中产生动力中断的缺点。

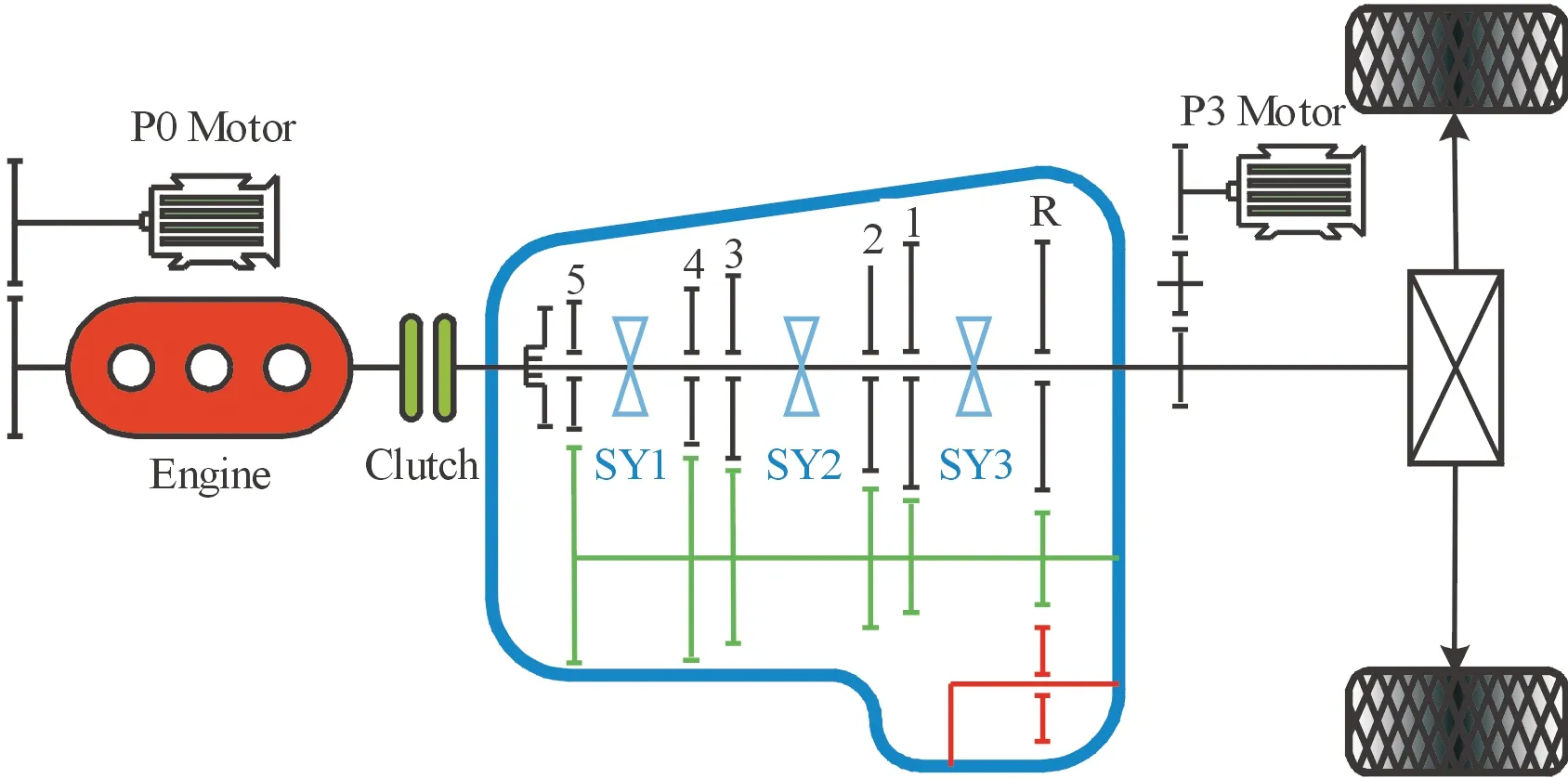
图1 基于AMT的混合动力汽车结构示意图

以搭载该系统的某车型为研究对象,原车型部分整车参数如表1,发动机转矩和油耗特性如图2、图3。

表1 原车型整车参数

图2 发动机转矩特性

图3 发动机油耗特性

2 考虑不同速比组合下换挡规律变化的耦合装置速比优化方法

传动系速比优化是一个多目标寻优问题,评价指标为汽车的经济性和动力性,但这二者之间的关系是矛盾的,要同时兼顾动力性和经济性一直是速比优化的难点[14-15]。此外,不同车型对于动力性和经济性的设计指标各不相同,难以用统一的量化指标去衡量,且需要经过多次调整。因此,编写速比优化程序非常有必要,利用程序能够循环计算的特性,计算出所有可能性的速比组合的动力性和经济性指标,设计人员再从中选取出合适的速比组合作为结果。

2.1 多线程速比优化程序总体框架

程序的主体计算流程分为4部分,包括:筛选组合、换挡规律计算、动力性约束计算和油耗计算,具体如图4所示。

程序会通过输入的设计指标计算出最大、最小传动比,通过多重约束计算得到各中间单位的速比范围。将在范围内的值形成组合并排序,代入到换挡规律计算和动力性约束计算中,以验证是否满足动力性指标,即动力性约束。

图4 优化程序主体计算流程框图

动力性约束是计算汽车从原地汽车起步到加速的时间,期间节气门开度为最大,采用动力性换挡规律。将计算得到的时间与输入的需求时间对比,筛选出合适的组合,进行下一步的计算。

经济性油耗则是通过经济性换挡规律,再根据输入的目标工况和发动机工作状态计算得到。从上述分析可以看出,如果定义子程序计算完成为一个循环,那么从得到第一个存在的速比组合开始,到程序计算完成,需要经历3个循环。若采用单个线程运行,会有流程慢、计算量大等缺点。因此,本文采用并行计算的方式,在计算换挡规律的同时运行子程序。此方法能将运行3个循环的时间减少为1个循环的时间,大大提高程序的运行效率。

2.2 目标函数和函数变量

程序设计的整体思路为:将工况时间离散化得到关于速度和时间的变化,并将其划分为N段,从而得到关于发动机工况状态和时间的变化[16],期间按照经济性换挡规律执行换挡流程。随着工况的运行将单位时间油耗量放入矩阵,然后通过矩阵累加得到总油耗,数学表达式为:

(1)

式中:E为汽车在循环工况下的油耗量(g);fuel为发动机的燃油消耗二维表,在不同发动机转速和转矩下会产生变化。选取动力耦合装置的传动比为优化变量:

X= (ig1,ig2,ig3,ig4,ig5)

(2)

式中:X为优化变量;ign为动力耦合装置n挡位的速比。因为经济性计算为最后一环,X已经过了多重限制约束,所以直接代入计算。

2.3 耦合装置传动比约束条件

约束条件包括:最大最小传动比约束、偏置等比分配约束、冲击度约束和动力性约束。

图5 速比约束的计算流程框图

1) 最大最小传动比约束

最大传动比要求能满足最大爬坡度,最小传动比要求能满足最高车速,其公式如下:

(3)

(4)

式中:m为汽车的质量(kg);f为汽车的滚动阻力系数;αmax为最大爬坡度(%);r为汽车的车轮半径(m);i0为主减速器的减速比;ηt为传动系总效率,取0.9。

2) 偏置等比分配约束

目前,动力耦合装置和变速器速比分配方法有等比级数分配和偏置等比级数分配。等比级数分配能充分利用发动机提供的功率,提高发动机的动力性。因此,采用等比级数对五挡的动力耦合装置进行分配,分配规律如下:

(5)

但在实际生活中,汽车位于高挡位的驾驶时间和驾驶里程,以及驾驶员对高挡的利用率均大大低于低挡,且速比阶越小越节油,换挡也方便,故现在多采用偏置等比级数来分配速比[17]。

所以,对传统的等比级数进行修正,使相邻两挡之间的传动比之差随挡位增加而减小,而在原等比速比基础上变为偏置等比速比,约束条件如下:

(6)

3) 冲击度约束

为了避免各挡位速比取值不合理,需要按照工程经验公式对各挡位速比范围进行限制[18]。

(7)

(8)

(9)

(10)

式(7)—(10)为偏保守的经验公式,是工程师在设计速比为考虑相邻挡位速比值相差过大而产生换挡冲击影响汽车驾驶员舒适性[19],而人为地限制各挡速比的上下限范围。

4) 动力性约束

动力性约束条件包含0～50 km/h加速时间和0～100 km/h加速时间,其公式如下:

(11)

(12)

式中:Ft为汽车的驱动力(N);Ff为汽车的滚动阻力(N);Fh为汽车的迎风阻力(N);δ为旋转质量转换系数;t1和t2为汽车0～50 km/h和0～100 km/h加速时间(s)。t1和t2均需要根据设计需求来制定,为动力性的最低标准,不满足标准的速比组合不会被程序纳入计算。

动力性约束的目的是判断得到的速比组合是否符合动力性要求,以0～100 km/h时间的计算为例,其计算流程如图6所示。

图6 动力性约束计算流程框图

对前文中多重约束得到的组合进行动力性的计算,运行前需要手动输入动力性的约束指标,即百公里加速时间的最大时间标准。程序开始计算前需要导入发动机转矩特性、整车参数和前文计算的动力性换挡规律。默认发动机初始转速1 000 r/min,节气门开度100%。根据发动机转矩特性查表得到输出转矩,结合整车参数得到当前车速。结合动力性换挡规律,如果需要换挡则重新返回到上层计算,当车速达到目标车速后,开始下一个组合的计算。期间将每个组合所耗费的时间与设计所要求的时间进行对比,筛选出满足条件的组合进入到下一步计算中。首先定义发动机转速向量,节气门开度的向量。根据发动机转矩特性、油耗特性和已有的转速向量得到转矩和油耗率。做出当前节气门下相邻挡位速度和油耗率、加速度曲线,并求其交点作为汽车的换挡点[20],换挡规律计算流程见图7。

图7 换挡规律计算流程框图

由于汽车最大爬坡度和最高车速不变,因此,最大、最小传动比不变化,即只对中间挡位的速比重新进行优化,具体变化范围如表2所示。

表2 各挡传动比范围

2.4 经济性的油耗计算

计算油耗前,需要输入目标工况、发动机参数、整车参数和工况要求油耗量。油耗的计算流程如图8所示。

图8 油耗的计算流程框图

在计算流程中的难点和重点有二:一是通过将时间和工况离散化后,需要选择恰当的时间步长以维持油耗量计算的精准度;二是当汽车需要换挡时出现单位时间油耗量被重复计算的情况。

针对上述问题,缩短单位计算时间和增加判断模块可以解决。单位计算时间是影响油耗量计算的重要因素,时间步长取得越小,油耗量越精准,但程序运行时间会增加。由于需要计算的速比组合较多,因此需要选定合适的时间步长。根据本文研究的目标将时间步长设定为0.5 s。此外,油耗矩阵在每次循环定义只能写进一次,因此不会出现重复计算的问题。

即使经过了多种约束的限制,还是存在数量庞大的速比组合,为了方便观察和查找,将每种速比组合进行编号,并将其放入向量中。

3 优化计算结果及分析

油耗计算输入的工况为NEDC工况,该工况由4个城市低速循环和1个城郊高速循环组成,能体现汽车在不同工况下对发动机需求转矩的变化,具体变化如图9所示。程序运行后生成如图10所示的油耗曲线。

图9 NEDC工况车速曲线

图10 油耗曲线

在满足约束条件下,共有46 914种可能的速比组合,针对每一种速比组合,程序会对它们进行编号。随着速比序号的增大,二挡的速比值增加,三挡、四挡速比值则呈周期性变化,从而对应的油耗量也呈周期性变化。可以看出,各挡位的速比值对油耗都会有影响,但是二挡的速比值对油耗影响最为明显,其次是三挡和四挡。若单纯考虑油耗则第一个周期开始的速比组合油耗最低,此时的二挡速比值处于最小值2.38。之所以呈现这种现象,是因为在城市循环工况下,汽车长期处于低速状态,历经多次停车起步,因此较小的二挡值能改善发动机的油耗。

在百公里速度加速过程中,使用到了多个挡位,其中三挡使用时间最短,一挡、二挡的使用时间最长,且对加速时间的影响最大,如图11所示。图11(a)展示了不同二挡速比值对汽车百公里加速时间的影响,图11(b)为二挡速比值随速比组合序号的变化。

图11 二挡动力性的变化曲线

从图11(a)中可以看出,随组合序号的增加,即二挡速比值的增大,汽车加速时间缩短。结合前文油耗规律,可以发现,满足单位周期内经济性最好的点往往其动力性较为不好,并随二挡速比值的增加其动力性会越差。因此,设计人员可根据汽车设计之初的需求,在动力性和经济性间做出一定的取舍。

根据本文研究对象的动力性设计最低需求,选取出油耗最优的点,具体参数如表3所示。

表3 优化前后各参数的变化

4 系统建模及仿真分析

针对程序计算得出的结果还需要搭建仿真模型进行验证,因为程序的计算结果是基于静态计算的基础上的,而实际上汽车运行中各参数时时处于动态变化中。需要对优化前与优化后汽车的动力性和经济性进行对比,来验证程序计算得出的结果对降低整车油耗是否有效。

4.1 动力性仿真

用一挡起步,以最佳换挡时间操控挡位依次至高挡,节气门开度始终处于100%开度下,以该时间为最后评价动力性的标准[21]。在进行动力性仿真前,需要计算汽车在优化前后的动力性换挡规律,并在仿真模型中对此规律进行验证,通过计算得出的结果判断优化后的动力性换挡规律是否合理。以此为前提,搭建动力性的仿真模型,其动力性仿真的控制逻辑如图12所示。

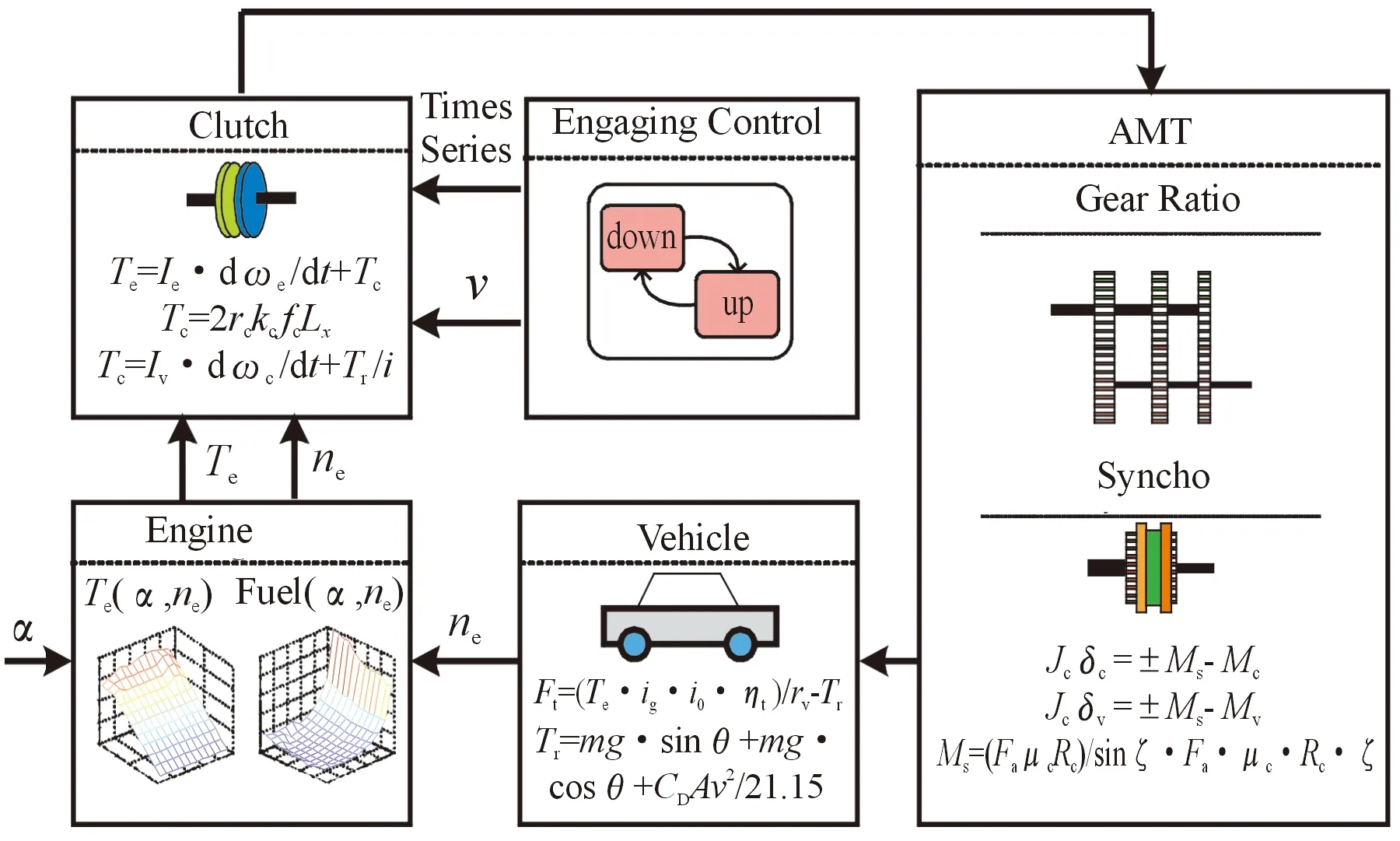
图12 动力性仿真控制逻辑示意图

在其他参数不变的情况下,得到的动力性换挡规律如图13所示。

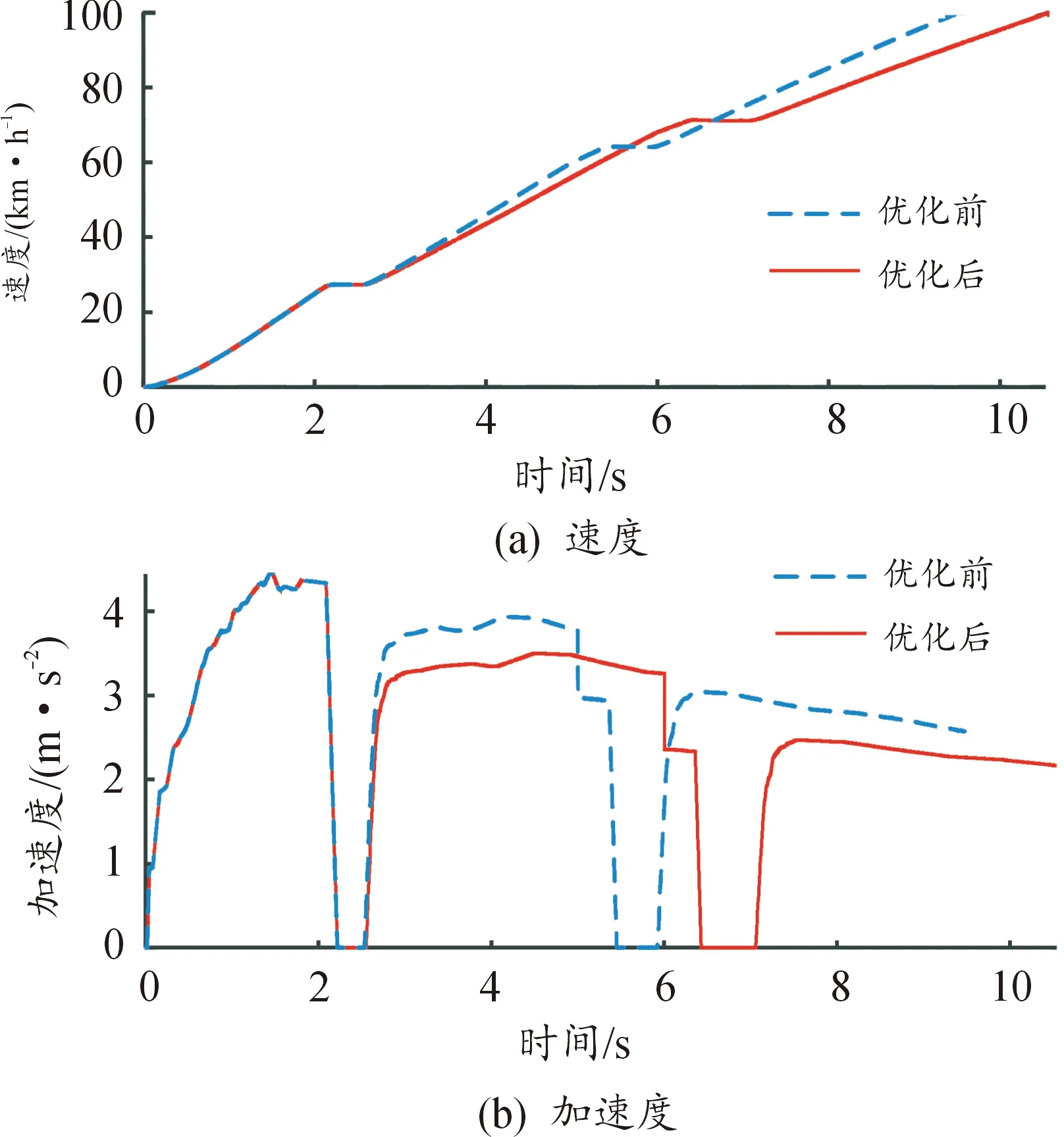
图13 动力性仿真曲线

图13是速度和加速度随时间的变化曲线。从图中可以看出,车辆在切换到二挡之后动力性开始出现变化,经过优化后的汽车动力性有所降低,这是由于优化后的变速器速比值降低所引起的。从图13(b)中可以看到,换挡过程中存在动力中断,这是由于仿真计算模型中加入了换挡过程的动态控制以及AMT本身的特性,是静态计算所不能呈现的。

4.2 经济性仿真

在计算经济性仿真前,需要计算汽车在优化前后的经济换挡规律,并搭建仿真模型,其控制逻辑如图14所示。与动力性仿真模型不同的是,经济性仿真模型需要加入驾驶员模型和发动机油计算模型。又因为换挡时间对油耗影响不明显,所以在建立经济性仿真时没有离合器和同步器的动态模型。

图14 经济性仿真控制逻辑示意图

优化前后的经济性换挡规律仿真结果如图15所示。

图15 经济性换挡规律曲线

经过经济仿真得到优化前后发动机工作状态,如图16所示。

图16 优化前后发动机工作状态

图16中呈现了发动机工作点变化区域和不变区域,在城市工况中汽车启停频繁,较长时间行驶在低速中,发动机大多数时间工作在低转速区域内,此时多处于工作点变化区域。在此区域汽车以较低速度行驶,经过速比优化后发动机工作点被拉高,发动机运行在更经济省油的区域内,所以会较优化之前有更好的燃油经济性。对于之后的城郊工况,当整车需求转矩不大,节气门开度较小时,也能优化发动机的工作点。当汽车行驶速度增大,需求转矩增加,此时最高挡位的使用时间较多,由于优化前后汽车的最高挡位速比没发生变化,所以这段工况较优化前无太大差别。

综上所述,在低转速,中、小节气门开度下,经过速比优化的汽车发动机工作点被拉高,经济性得到了有效提高。

最后通过对经济性换挡规律和动力性换挡规律的仿真得到了优化前后的结果,如表4所示。

表4 换挡规律优化前后仿真结果

从表4中数据可以看出,优化后车辆的动力性虽然降低了11.15%,但经济性提高了4.44%。

5 结语

1) 针对速比优化中易陷入局部最优、不同速比组合下动力性经济性换挡规律会发生变化的情况,提出一种基于穷举法的动力耦合装置速比优化方法。通过该算法得到的结果覆盖所有速比组合,能直观体现不同速比组合下油耗和动力性的变化。此方法能保证获得全局最优的计算结果,且当经济性和动力性需求发生变化时,能根据计算结果快速选取出所需的速比组合。

2) 针对穷举法计算量大的问题,在以往速比优化工作基础上对速比组合加入了偏置等比约束、冲击度约束和动力性约束,减小了速比搜索范围。在不同速比组合下换挡规律的计算中,采用多线程技术进行优化计算,使计算时间保持在合理范围内。

3) 对优化前后整车动力性和经济性进行仿真分析,在动力性变化不大的情况下,提高汽车在低转速和中、小节气门开度时的经济性,有效降低了汽车在起步和低速行驶下的油耗量。