车用永磁同步电机铸铝合金机壳热疲劳寿命预测

何联格,袁 洲,石文军

(1.重庆理工大学 汽车零部件先进制造技术教育部重点实验室, 重庆 400054;2.北京信息科技大学 现代测控技术教育部重点实验室, 北京 100192;3.重庆青山工业有限责任公司, 重庆 402761)

0 引言

永磁同步电机因其体积小、功率密度大等优点,有着广泛的应用前景[1-2],也正是因为其功率密度的不断增加,导致其所受的电磁和热载荷也在不断增加,而使电机的可靠性和寿命受到严重影响[3-4]。与一般电机相比,车用电机工作环境温度较高,运行工况多变,导致机壳长期在较高交变温度下工作,虽然机壳在电机运行额定工况下,短时间内不会出现疲劳损坏,但在电机交变运行工况下机壳经常会出现疲劳裂纹,这对于车用电机而言这会造成噪声、机壳内吸入灰尘、冷却液泄露等问题,从而导致电机性能下降或损坏。

现目前已经有不少研究人员和学者对电机部件的强度和寿命进行了研究,但主要集中在电机转子上。邓承浩等[5]通过有限元分析转子在不同的转速和不同的过盈量配合下的强度,并进行疲劳寿命计算,得到比较合适的配合方式,但是没有将转子的热应力纳入考虑范围;林巨广等[6]以一台30 kW的永磁同步电机作为研究对象,基于传热学理论建立三维温度场模型,并结合温升试验验证仿真精度,分析了在离心力与热应力在热机耦合下对转子应力的影响;王天煜等[7]基于温度场和应力场的耦合,计算得到转子在正常运行工况下的应力分布,以及强度变化规律。以上文献在对转子的强度分析中表明,温度对强度的影响十分大,所以在电机各部件的结构分析考虑温度是十分必要的。但是针对电机机壳,研究人员主要考虑振动和装配。张宇[8]采用有限元法对机壳的振动进行了研究,并对多种模型下的机壳进行了对比分析,得到对振动比较有利的机壳模型;魏志远[9]介绍了一种有利于电机机壳装配的过盈量的计算方法。对机壳的研究都很少关注机壳的强度,特别是在热应力下的寿命预测。

本文选择电机的2种工况进行研究,其中 4 000 r/min、40 N·m作为额定转速下的一般工况,4 000 r/min、87 N·m作为额定转速下的持续工况。由于在不同工况下,电机的温度会有所不同,因此要首先对电机温度进行采集,以保证在仿真条件与现实的电机运转状态相似,结合电机的主要损耗,对电机温度场进行仿真计算,并与温升试验结果对比,发现仿真结果最大有8.8%的误差,在允许范围之内;其次通过试验得到了电机机壳材料热机疲劳寿命预测模型的相关参数,并在强度计算中将所得的电机温度场映射到应力场中,分析机壳所受热应力;最后利用热疲劳仿真计算预测机壳在热应力作用下的寿命。研究结果表明机壳寿命满足可靠性设计要求,可作为设计和材料选择的参考依据。

1 温度场计算

1.1 电机的基本参数

本文的样机如图1所示,电机基本参数见表1所示。通过试验确定电机在4 000 r/min下时,温度达到绝缘材料极限温度(150 ℃)时的转矩为 87 N·m。

图1 样机实物

表1 样机基本参数

1.2 台架试验

搭建试验所需台架,如图2所示。将试验电机放置到环境舱,以模拟车用电机的实际工作条件,得到不同工况下较准确的环境温度,并同时采集电机绕组端部温度。试验采用热电偶法,由于电机绕组端部温度较高,且绝缘材料直接受其影响,所以监测绕组端部温度。

图2 试验平台实物

在试验中,将电机运行30 min后的温度视为稳定温度。采集得到电机在4 000 r/min时不同转矩下后的环境温度和绕组端部温度如表2所示。

表2 不同工况下的环境温度和绕组端部温度

1.3 热源计算

准确计算电机各部件的损耗是计算电机温度场的前提[10]。

根据文献[11-12]采用Bertotti分离模型,各部分损耗按如下公式进行计算:

(1)

式中:PFe为总铁损;Ph为滞后损失;Pc为涡流损耗;Pe为异常损耗;kh为滞后损失系数;kc为涡流损耗系数;ke为异常损耗系数;f为电流频率;Bm为磁密度的振幅;a为常数系数。

永磁体的涡流损耗可以利用以下公式计算[13]:

(2)

式中:δPM为永磁体的电导率;fmn为mn次谐波频率;P为电机的极对数;ωPM为永磁体沿电机圆周方向的跨距;Nlam为永磁体沿周向分块数目;VPM为永磁体的体积;Bmn为永磁体内mn次磁通密度谐波幅值。

铜耗主要由电阻损耗和高频附加损耗组成,在电流频率较低时,铜耗可利用常规计算公式得到。

Pcu=mI2R

(3)

式中:Pcu为绕组铜耗;m为电机相数;I为相电流;R为绕组内阻。

风磨损耗采用以下经验公式可得到。

(4)

式中:PF为风磨损耗;n1为转子的转速;Dr为转子外径;lr转轴向长度。

为了方便热仿真对热源加载,通过式(5)计算分别得到各部分的生热密度如表3所示。

Q=P/V

(5)

式中:Q为电机中各部位热生成率;P为电机各部件的损耗;V为电机各部位的体积。

表3 电机各部件生热密度

1.4 温度场仿真模型

经过对模型网格质量、仿真分析时长等综合考虑,根据文献[14]提出假设条件,建立仿真模型如图3(a),将绕组等效为实心一体模型如图3(b)所示。

图3 温度场简化模型示意图

1.5 传热学理论

根据能量守恒定律及傅里叶定律,各部件的导热微分方程,而主要的导热边界条件有3类,分别是:物体表面温度为恒定值的第一类;物体表面具有固定的热量,存在热传导称为第二类;物体表面上存在对流换热的称为第三类,涉及式(6),由文献[15]可得。在使用仿真软件对温度场求解的过程中仅考虑第二类和第三类边界条件,其中绝热面以及2个固体相互接触的2个壁面采用第二类边界条件,流与固耦合面为第三类边界条件。

(6)

式中:λx、λy、λz分别为电机内各介质在x、y、z方向的热导率;T为物体的温度;qv为热生成率;ρ为物体密度;v为物体质量热容;Tw为边界温度值;τ为时间项;S1、S2、S3为物体边界;Tf为流体温度;α为对流换热系数。

由于在绕组表面由绝缘漆,绕组之间有气隙,定子槽内有不均匀分布的槽内浸漆层和绝缘纸等,为了方便添加材料参数,对绕组进行合理的等效处理,根据文献[16]将各绝缘材料等效为一体,如图3(b)所示。

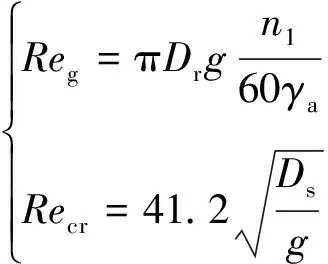
(7)

式中:Reg为等效气隙雷诺数;Dr为转子外径;n1为转子转速;γa为空气动力粘度;g为气隙厚度;Recr为等效气隙临界雷诺数;Ds定子铁芯内径。

本文经过计算得到Recr值为552.8,当转速小于3 500 r/min,Reg小于Recr,气隙等效导热系数与空气导热系数值相等;当转速大于3 500 r/min,Reg大于Recr,此时气隙等效导热系数λa可根据式(8)得到。

(8)

式中:λa为气隙等效导热系数。

1.6 边界条件设置

本文对电驱动系统在不同工况下进行研究,设置了不同的边界条件,设置如下:

1) 以实际车用电驱动系统运行环境为参考,将电驱动系统环境温度设置为85 ℃;

2) 冷却液入口设置为速度入口,流速为8 L/min,冷却液温度根据不同研究工况的需要设定;

3) 冷却液出口设置为零压力出口;

4) 仿真计算中所有流固耦合面兼为无滑移边界;

宝格丽Octo Finissimo陀飞轮自动上链腕表厚度仅为3.95毫米，第四次刷新世界纪录。Octo Finissimo陀飞轮自动上链腕表作为2018年又一具有里程碑意义的新作，充分诠释了宝格丽在腕间时计上所赋予的非凡艺术造诣。Octo Finissimo镂空陀飞轮腕表与Octo Finissimo自动上链腕表均在去年的日内瓦高级钟表大赏斩获大奖，为品牌赢得业内一致认可。

5) 其余边界条件参考文献[14,18]进行处理。

1.7 温度场结果分析

通过温度场仿真得到机壳在2种工况下运行30 min后的温度分布云图。图4(a)为一般工况,机壳最高温度为67.9 ℃;图4(b)为持续工况,机壳最高温度为75.5 ℃。通过对比虽然在2种工况下转矩相差较大,但是从机壳温度分布上看,温度较高处都在近变速器端,该处温度主要受到环境温度的影响,相对的,进水口附近的温度却比较低,温度数值上与冷却水相近,而且温度分布随着水流方向逐渐升高,说明机壳温度还直接受到冷却水温度和流向的影响。

图4 机壳在不同工况下的温度场分布云图

在台架温升试验中一般采用热电偶法,因为绕组端部温度最高,所以试验主要监测绕组端部的温升状况,当绕组温度趋于稳定后,且在10 min内温度变化不超过1 ℃,则认为绕组温度达到平衡,表4为不同工况下温度达到平衡后的数值。

表4 仿真与试验温度

在工程问题中,若温度场仿真结果与试验结果的误差在10%以内,则认为温度场仿真结果是可行的,可以用于后续仿真计算。

将不同工况下绕组端部温度与台架温升试验数据对比,可以看出误差最大为8.8%,在允许范围10%之内,可以作为下一步计算的输入。

2 强度计算

2.1 材料试验

根据本次研究所用机壳工作的实际情况,制定的铝合金材料试验温度为40、80和150 ℃,试验过程参照国标GB/T 228.2—2015进行[19]。试验件尺寸及实物分别如图5—6所示。

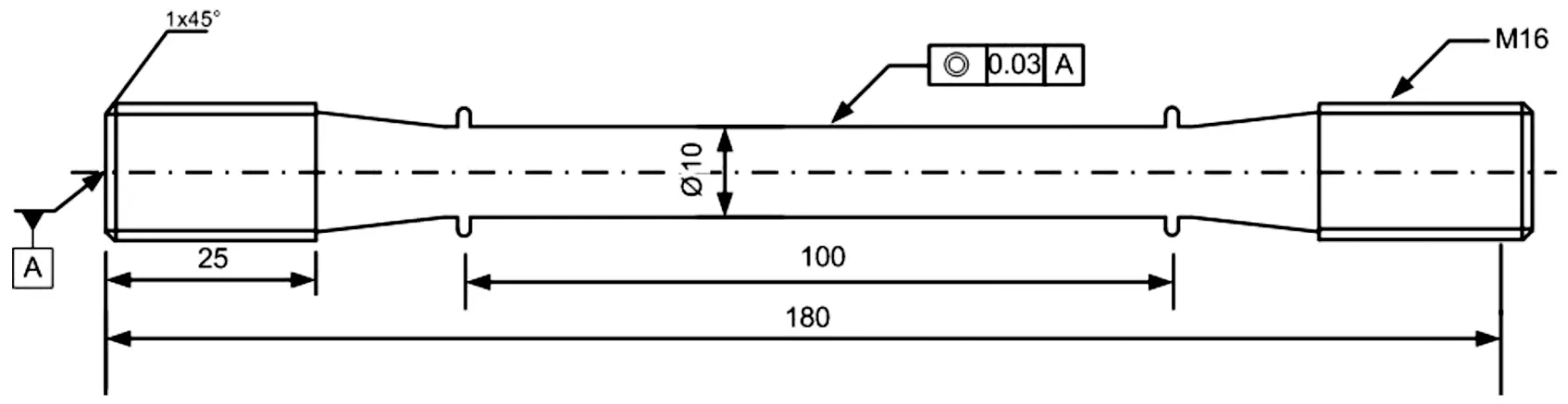
图5 试验件尺寸

图6 试验件实物

根据试验结果并整理数据得到了铝合金在不同温度下的基本参数如表5所示,同时得到铝合金材料在不同温度下的应力应变曲线,如图7所示。

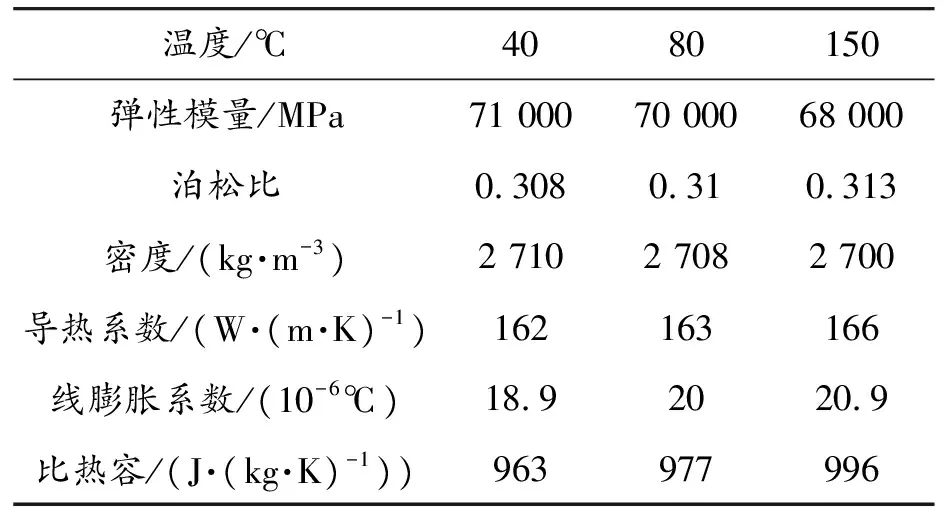
表5 机壳的材料参数

图7 机壳材料在不同温度下的应力-应变曲线

2.2 强度分析

在不同的温度场下进行机壳的应力计算。图8为在有限元软件中加载的温度载荷变化情况,在分析中0-a为电机在静态下时的20 ℃,a-b为电机在4 000 r/min、40 N·m下的温度分布,b-c为电机在4 000 r/min、87 N·m下的温度分布。

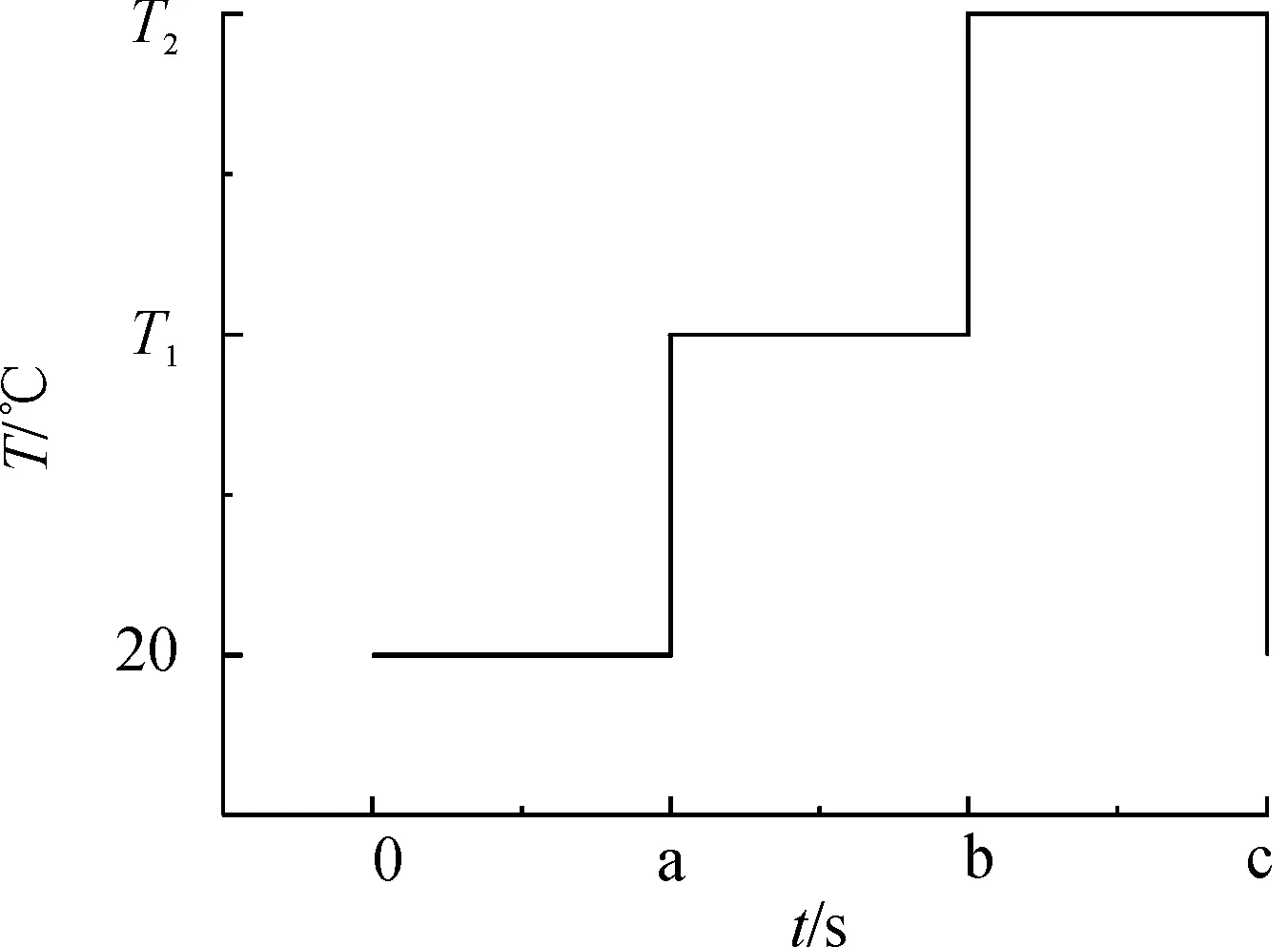
图8 热载荷曲线

为了对电驱动系统机壳进行强度分析,根据图7拟合得到如图9所示的屈服应力与温度之间的关系曲线,在67.9 ℃和75.5 ℃两个不同温度下的屈服应力分别为231.3 MPa和228.6 MPa。

图9 机壳材料在不同温度下的屈服应力曲线

此处同样采用ABAQUS商业软件作为分析软件,在边界约束时将所有的螺栓孔进行全约束,并将1.7节中得到的温度场计算结果作为热载荷加载到机壳上。初始温度为20 ℃,得到不同工况下的应力和应变分布云图,如图10—11所示。电机在一般工况运行时,机壳的最大应力为187.9 MPa,安全系数为1.23,最大等效应变为1.07%;电机在持续工况运行时,机壳的最大应力为192.6 MPa,安全系数为1.19,最大等效应力为1.34%。通过对比发现,应力集中区域与温度较高的区域相对应,说明在约束和边界条件相同的情况下,温度与应力成正相关。

图10 应力云图

图11 应变幅云图

3 寿命预测

为了对电驱动系统机壳在连续工况下的寿命进行预测,需要对机壳材料进行疲劳试验。根据铝合金机壳的特点,设计合适的疲劳试棒,如图12所示。试验温度为40 ℃和150 ℃,根据国标GBT 15248—2008进行[20]。

图12 疲劳试棒

通过试验得到机壳材料分别在40 ℃和150 ℃的循环滞后环,如图13—14所示,在每个温度下的应变幅值分别为0.15%、0.30%和0.4%。随着温度的升高,在相同应变幅值下,滞后环轨迹与应力-应变初始轨迹偏越来越大,特别是在小的应变幅值下,这说明在温度升高后改善了材料的延展性和塑性变形能力。同时温度升高,应变幅值一定,拉压过程中所对应的最大应力值逐渐降低,这与图7中的应力-应变曲线所显示结果基本一致。再结合式(9),可以得到仿真计算时需要的一系列如表6中的参数。

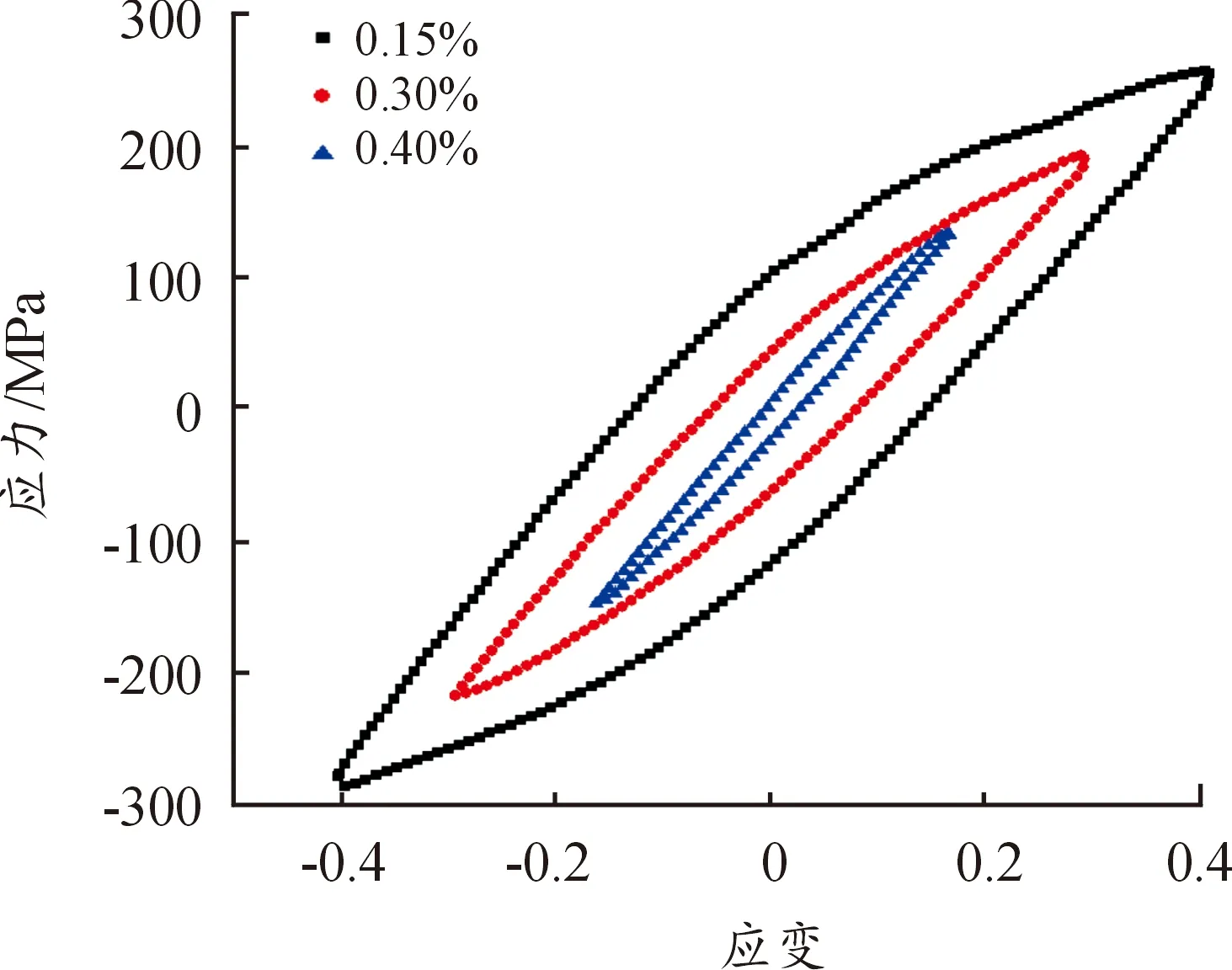
图13 40 ℃时铝合金材料的循环滞后环曲线

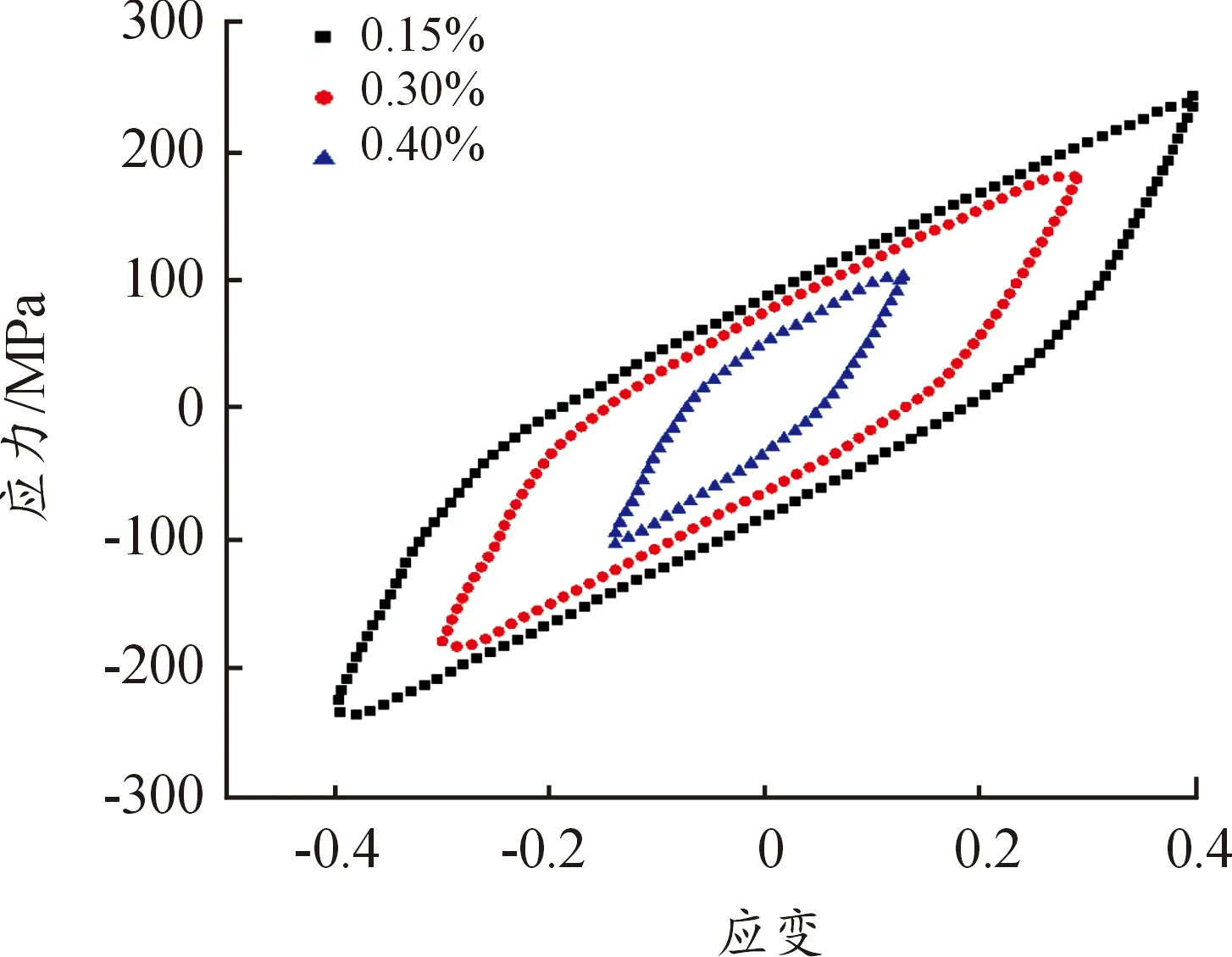
图14 150 ℃时铝合金材料的循环滞后环曲线

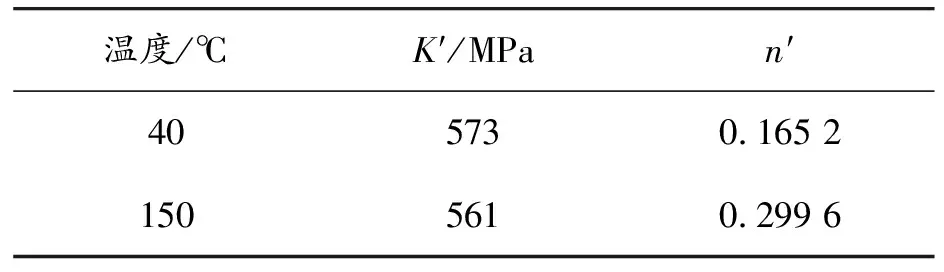
表6 铝合金在不同温度下的参数

σa=K′(εpa)n′

(9)

式中:σa为应力幅值;εpa为应变幅值;K′为循环强度系数;n′为循环应变硬化指数。

机壳材料在40 ℃和150 ℃的应变与疲劳寿命之间的关系图15所示。

图15 不同温度下铝合金材料的应变-疲劳寿命关系

从图15中可以看出,材料的最大应变与寿命呈反比,在低温下因为材料的的塑性应变性能较差,所以在相同的寿命下塑性应变较低,结合式(10)的Manson-Coffin模型,可以对图中寿命与应变之间的关系进行合理解释[21],并且可以得到在仿真中所需的各种参数在不同温度下的具体数值,见表7所示。

(10)

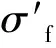
表7 机壳的材料在不同温度下的Manson-Coffin模型参数

结合机壳的热应力计算,通过材料试验得到的材铝合金料参数,利用FEMFAT软件对机壳在热应力条件下的寿命进行预测。图16为计算结果,电机机壳在热应力的作用下,从静态的20 ℃到最高温度过程中,对比图4和图10发现,损伤分布与温度和应力分布相对应,最大损伤为 3.37×10-5,将其转换成循环周次,可得循环周次为 29 673次,不会出现低周疲劳现象,且满足设计要求。

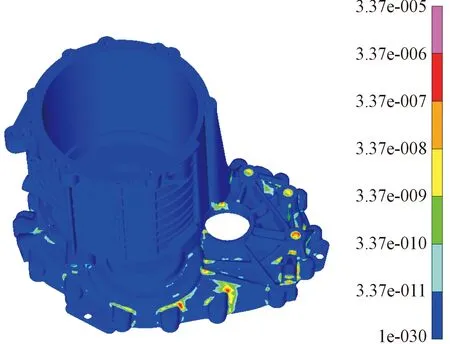
图16 机壳损伤云图

4 总结

在电机台架试验和基本材料试验的基础上,通过有限元法对电机在4 000 r/min、40 N·m和4 000 r/min、87 N·m下的温度场、应力场,以及寿命的仿真计算,得到以下结论:

1) 对2个工况下的温度场进行仿真计算和试验,在工况不同时环境温度发生变化,机壳的温度随之改变,温度场仿真结果与实验结果温度误差在允许范围之内。

2) 经过材料试验之后得到机壳的基本材料参数,2个工况下的热应力值分别为187.9 MPa和192.6 MPa,温度越高机壳的安全系数越低。

3) 通过对机壳的寿命预测,得到机壳可在电机处于室温与极限高温之间时循环29 673次,不存在低周疲劳现象,满足机壳设计要求。