大单元视角下的数学建模和数学探究
2023-06-07施维
施维
【摘要】大单元视角下,教师应如何贯彻落实对现实问题进行数学抽象,进而建立数学模型,以及如何落实探究式教学,本文借助教材中的三角函数与杨辉三角进行一些研究.
【关键词】高中数学;大单元教学;数学建模
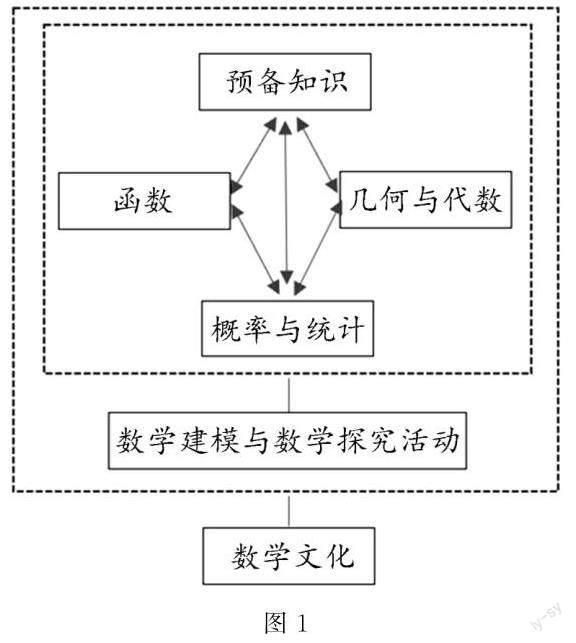
《普通高中数学课程标准》(2017年版)(以下简称《新标准》)中把函数、几何与代数、概率与统计、数学建模与数学探究活动作为高中数学知识的四条主线内容,这四条主线与初中数学中的四条主线相一致,知识难度呈螺旋状上升,增加了预备知识.这四条主线与预备知识和数学文化间的基本关系如图1.
《新标准》中提出六大数学学科核心素养,数学建模这一核心素养是指通过对现实生活中的实际问题进行数学抽象,让学生用数学语言表征问题、用数学方法构建模型从而解决问题的素养.数学探究活动是指围绕某个具体的数学问题开展自主探究、合作研究并最终解决数学问题的过程.数学探究与数学建模可以很好地培养学生的创新意识与实践能力,同时学以致用,体会数学来源于生活又可以运用于生活中,从而使数学与生活不再脱节.
1 大单元的框架结构下进行的数学探究活动和数学建模
新教材在设计时,知识符合学生的认知规律,采用螺旋上升的方式编排,在各个主线的研究过程中很注意整体性,以及前后知识之间的上下位关系.例如,在函数主线中,要解决函数的概念、函数的性质、基本函数类、函数的应用、思想和方法.例如,在前面几节介绍完函数的概念、性质以后给出幂函数的图象与性质,通过前面一直贯穿的数形结合思想来研究幂函数的性质,为后来学习其他几种函数提供了方法支持.幂函数、指数函数、对数函数都存在增函数的情况.
例如 以一次函数y=kx(k>0)、指数函数y=ax(a>1)、对数函数y=logax(a>1)为例来研究三种函数的差异,而这种差异正是不同类型现实问题具有不同增长规律的反映.接下来分析三种不同函数的增长方式,以便用不同的函数模型刻画现实生活中的变化规律.刻画循环往复、周而复始规律的最典型的函数模型就是三角函数.而具有周而复始变化规律最典型、最熟悉的模型就是匀速圆周运动,接下来在整个三角函数一章始终贯穿用单位圆来研究三角函数,借助圆来研究三角函数就是这一章节的主线,通过这些可以看出教材的设计很注重整体性和连贯性.
在三角函数部分,开头就用圆周运动引入,整个章节通过单位圆定义三角函数的概念,也是通过单位圆来研究三角函数的性质以及两角差与和的正弦余弦公式等,以便于学生理解三角函数是用来刻画周而复始现象的.再来回归现实解决问题,通过对筒车模型的研究,一是把数学与中国古代人们的智慧结晶相结合;二是便于学生理解y=rsinωx+φ+h中各个字母的含义,为接下来进行的数学探究A,ω,φ对y=Asin(ωx+φ)图象的影响奠定认知基础.最后研究了生活中常见的一些三角函数可以刻画的模型,如弹簧振子、交变电流、潮汐现象等.又把数学与生活联系起来,整个章节的构想具有整体性,且具有生活气息,使数学活了起来.
2 数学建模和探究式教学所遵循的原则
2.1 自主探究与小组合作相结合的原则
数学探究和数学建模的意义在于培养学生成为全面可持续发展的人,教学过程中要充分体现学生是学习的主人,必须先自主探究和独立思考,再进行小组讨论,经过小组整合以后,整理提出的问题,进而寻求解决问题的办法.
2.2 以问题为主线的原则
探究式教学是以学生自主思考、合作探究为主的教学模式,数学建模也是由学生为主体的活动,必须贯彻教师是課堂的引导者,以问题引导的方式保证学生课堂主体的地位.好的问题是高效课堂的保障,学生想在有限的课堂教学时间内完成高质量的数学建模和数学探究活动,教师一定要进行充分的备课,了解学情,设计一系列引导性的问题串,在学生理解困难处和疑惑处搭建脚手架,使学生可以“跳一跳,摘个桃”,也就是问题的设计要符合学生的最近发展区.同时,课堂中教师要随时注意学生提出的问题,学生想到的问题可能不是正确的,但这就是学习的过程,符合桑代克提出的试误——联结学习理论,犯错证实学习在真实地发生.学生提出问题(哪怕是错的)比解决问题来得更为重要,能发现问题才是教育的最终目的.
例如 在高中数学人教A版选择性必修三第六章最后一节“数学探究:杨辉三角的性质与应用”中可以设计如下问题串.
问题1 对比二项式系数表与杨辉三角,你有什么发现?
追问1 请同学们观察这两个数表,你能把二项式系数表与杨辉三角统一起来吗?
结合教材中的两个图,可以发现杨辉三角比二项展开式多了一行,把第一行记为第0行,则杨辉三角的第n行的第r个数可以表示为Cr-1n,第n行就是(a+b)n的展开式的二项式系数.
问题2 先从整体观察杨辉三角中数字的结构,即杨辉三角这一数字三角形中数字排列的规律.
追问1 再细致地观察每一行、相邻两行、斜行等的规律.
追问2 通过画一画、连一连、算一算这样的数学实验,验算一下你发现的规律.
追问3 写出你发现的结论,这些结论能否用组合数表示?
通过问题串的形式,引导学生逐步地学会数学探究的方法,先是表征问题,然后就是带着问题,观察、思考、分析,提出有意义的数学问题,猜测、归纳和猜想,再到推理和论证,这就是一个完整的数学探究过程.带着问题使课堂更高效,这节课教学的重点是教会学生数表的探究方法.通过本节课,学生知道数学探究要观察,可以先整体再局部,先猜想再论证,先类比模仿再创新实践.
2.3 以信息技术辅助教学
人类已经进入大数据时代,数学的研究领域和应用范围得到的拓展,数学直接为社会创造价值,推动社会生产力的发展.同时信息技术的发展也能反哺数学的研究与教学,让数学建模和数学探究活动变得生动和有趣.直接的优势就是:计算机将数学建模问题和数学探究的求解变得异常直观、清晰、透彻.这也符合大数据时代数学的经济价值和应用价值,同时信息技术反作用于数学研究.
例如 高中数学人教A版必修第一册5.6.1匀速圆周运动的数学模型,通过筒车模型进行的数学建模活动,可以通过GGB软件把模型简化.
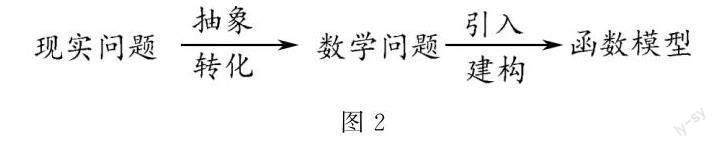
通过对几何图形的研究很容易把实际问题抽象转化为数学问题,进而解决数学问题,进一步引入、建构函数模型问题,经历的过程如图2.
同样地,在数学探究过程中,由于数学太抽象,配以动态的信息技术手段能使问题变得生动,学生不光可以听见还可以看见,甚至动手操作,这样数学探究的难度就会降低,如在5.6.2函数y=Asin(ωx+φ)中可以通过几何画板或者GGB软件来演示三个参数A,ω,φ对函数y=Asin(ωx+φ)的影响.
2.4 充分考虑学生的学情
《新标准》指出,数学教学也是教育的重要部分,其根本任务也是立德树人,最终要实现人人都能获得良好的数学教育,不同的人在数学上得到不同程度的发展的目的.而数学探究活动和数学建模活动就是实现这一目标的有效抓手,数学探究活动和数学建模都是以自主探究和小组合作来进行的.
例如 在高中人教A版数学选择性必修三中,对杨辉三角的性质与应用一节的数学探究,先进行自主思考,对数表的探究是个比较简单的任务,就是学生很喜欢的找规律,使每个学生都能思有所得,从而实现每个人都能学有所得.再进行小组交流,在思辨讨论中知识产生了,语言表达能力提高了,思维得以碰撞,眼界得以开阔.在分组时充分考虑学情,采用组间同质、组内异质的原则分组.小组交流时每个同学提出自己的意见,经过小组分析、辩论以后产生的才是知识.小组在激烈讨论时,以及全班同学共同研讨时,实际上就是在进行头脑风暴,就是创造性思维训练,最后就能实现对创新意识的培养.
3 数学探究活动、数学建模与数学文化一脉相承
杨辉三角是我国古代数学的伟大成就,教科书因为杨辉三角在数学和数学思维上的价值(人们研究数表由一行到多行,一两条性质到一系列性质,从个别到系统,都体现数学知识的获得过程,即由浅入深,由特殊到一般,通过杨辉三角的研究先整体再到局部,由观察到归纳到猜想论证,体现了完整的数学探究的过程),又具有审美价值和具有多元化的特性(中国、欧洲、阿拉伯等地的众多数学家都曾研究和应用它),对于培养学生的数学思维、开阔眼界有重要价值,从而设置了数学探究栏目,使学生通过数学探究活动提高认识的同时,全面提高学生数学学科核心素养,以此培养学生的民族自豪感和一探究竟的兴趣.
例如 在高中数学人教A版必修第一册“5.6.1匀速圆周运动的数学模型”一节中,筒车是我国古代发明的一种水利灌溉工具,经济又环保,至今还在农业生产中使用,明朝的徐光启就对筒车模型做过研究,而且画出了工作原理图,这里向学生呈现我国古代劳动人民的智慧结晶,吸引学生注意力,同时使学生产生学习的兴趣.
窥一斑而见全豹,在课本中贯穿很多数学文化知识,同时将数学探究与学生建模结合起来,使学生产生民族自豪感的同時,引起学生的兴趣,并开阔学生的眼界,使其理解数学来源于生活,又能服务于生活.
4 数学探究、数学建模与生活息息相关
数学建模和数学探究活动与生活息息相关,可以从生活中得到课题,如研究猪肉的化冻时间与温度的关系、跑步时体重与最佳燃脂心率的关系、鞋码与身高的关系,等等.生活中处处有数学,在运用数学知识解决实际问题的过程中,培养学生理论与实践相结合的能力,拓展知识面,培养学习兴趣,同时增强创新意识和实践能力.
5 结语
数学探究活动与数学建模活动不是单独存在的,依托于整个教学内容结构的整体设计,即大单元的结构,以某种知识脉络为主线,串联所有知识,抽丝剥茧从知识的发生发展娓娓道来,依托数学文化建构数学模型,使学生体会生活与数学的关联,同时可以开阔学生眼界,以模型为依托进行数学探究活动,感悟数学来源于生活.理论运用于实践,从知识内化为能力……这样行云流水般的设计使数学大单元的结构浑然天成,数学建模与数学探究活动穿插其中是知其然的过程,也是知其所以然的过程.
参考文献:
[1]许小颖.大单元视角下的初中数学单元教学研究[J].数学教学通讯,2022(05):46-47.
[2]葛开顺.深化高中数学建模教学,培养学生数学应用能力[J].数理天地(高中版),2023(03):86-88.
[3]张明刚.基于数学建模核心素养下的高中数学课堂研究[J].数学学习与研究,2023(01):122-124.
[4]顾向忠.关于“数学建模与数学探究”的高中数学教材比较研究——以苏教版、人教A版和人教B版为例[J].中学数学教学参考,2022(34):13-16.
[5]陈辉忠.培养高中数学建模素养的教学探究[J].数理天地(高中版),2022(17):52-54.
[6]狄闻于.高中数学建模与核心素养的分析和探究[J].中学数学,2022(19):92-93.
