探索多层材料复合设计中近场动力学理论的应用

郭一谚 尹 飞 姜玉海 杨 林 李国飞 童 鹤

（1．中国兵器集团第52 研究所烟台事业部，山东 烟台 264003；2．驻南京地区军事代表局驻烟台地区军事代表室，山东烟台 264003；3．陆军装备部驻包头地区第一军代室，内蒙古 包头 014033）

近场动力学是由美国Sandia国家实验室的杰出研究员Stewart Silling 博士于2000 年提出的[1]。其理论是基于非局部作用思想的一整套力学理论体系，通过求解空间积分方程描述物质力学行为，可以解决传统基于连续性假设的网格划分模型所面临不连续问题的奇异性和复杂性，是当前国际计算力学及相关领域的研究热点。

1 “态”基近场动力学理论的背景

近场动力学理论以求微分—积分的解来解决传统构建模型所面临的位移不连续（例如有裂纹的材料受力后断裂）、应变场不连续以及在不连续处存在导数没有定义的问题。最初提出的中心力本构模型的“键”基PD 模型有限制条件，即材料的等效泊松比只能为定值。为了解决这个限制问题，2007 年Silling 博士及其合作者提出了近场动力学的新本构模型：“态”基PD 模型（State-based Peridynamic models）。用“态”替换经典弹性理论中的“张量”，提出了一种同时兼顾连续（光滑）和不连续（不光滑）的空间映射。“态”的基本数学定义如下：m阶的态为函数A〈·〉：H→Lm，因此，向量ξ∈H在态A的运算下的映射就是m阶的张量，记作A〈ξ〉。理论上讲，“态”的数学定义可以到任意阶张量[1-4]。

2 近场动力学的三类PD 模型

近场动力学理论是研究质子与一定范围内的其他质子之间互相作用的物理现象。按照向量值函数的不同定义可以分为“键”基近场动力学和“态”基近场动力学。“键”基描述的是2 个质子点变形前、后大小相等、方向相对的相互作用力矢量，这2 个质子点间位移差允许位移场不连续，其相互作用取决于“键”的变形，因此泊松比被限制在一个独立的材料常数。“态”基指近场动力学的力态，它与其向量函数的变形位移及周围一定区域的物质点都有统计学意义。

基于“键”和“态”的概念，Silling 博士等在2007 年定义了2 个质子点之间的3 种不同本构关系，即常规“态”基PD 模型（Odinaray State-based Peridynamic Model）、“键”基PD 模型（Bond-based Peridynamic Model）和非常规“态”基PD 模型（Nonordinary State-based Peridynamic Model）[2-5]（3 种基本的本构关系模型如图1 所示）。

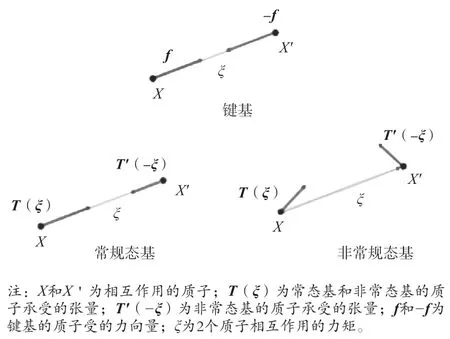
图1 3 种基本的本构关系模型

常规“态”基的PD 模型是一个标量态与一个向量态的乘积，力矢量的方向与“键”的方向平行。

“键”基的PD 模型只包括弹性常数，因此仅针对物质的整体变形，无法区分剪切变形和体积膨胀，可以看作是线性变化的常规“态”基模型。

非常规“态”基的PD 模型是变形前物质构造的应力与形状张量的乘积，可用力态2 个端点各自的应力张量表达（其力态方向和位移的形变方向可以不一致），且没有材料泊松比的限制问题，更适合计算材料断裂点及自然断裂纹。

基于这3 种基本的本构模型，Silling 博士针对裂纹、损伤过程的计算提出了材料质子间力矢量的断裂常用准则，计算裂纹面上单位面积的等效断裂功G0如公式（1）所示[2-6]。

式中：c为材料系数；s0为键伸长率的阀值（通常键的伸长率小于s0）；δ为物质中1 个点的周围领域的作用。

随着质子间相互作用的消失，质子之间的力矢量断开，连续质子间的相互作用断开就形成了裂纹（如图2 所示），因此公式（1）可以作为模拟运行过程中断或截止的判断准则。

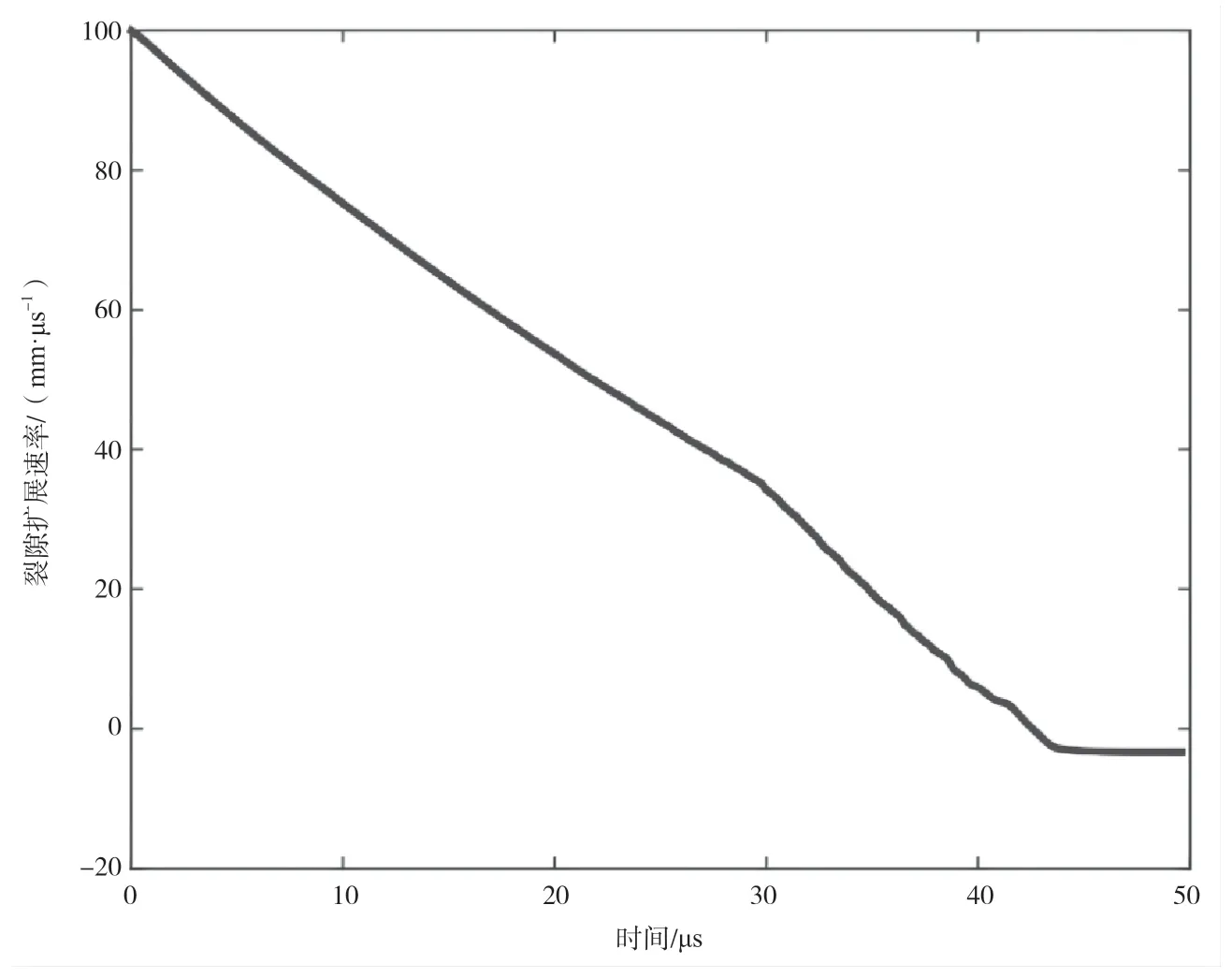
图2 裂隙扩展

3 近场动力学模拟计算弹靶作用的原理

荷兰TenCate 公司提到，传统的钢质组件可以抵抗质量小于10 g、速度约为800 m/s 的步枪子弹，质量相当或更小的多层材料复合装甲则可以对质量约为65 g、速度超过1 000 m/s 的穿甲弹或重机枪子弹进行防护。为了达到装甲轻量化和最佳防护效果，复合装甲材料的选择完全依赖实弹试验，费用、时间成本消耗过大，还会受地域环境的影响。因此，现代多层材料复合设计所采用的方法是逐渐形成基于实验研究的数据、历史经验数据及其试验结果，再结合模拟计算。常用的模拟本构模型理论基础是假设物质的质子位移变化是连续不断的，如果出现不连续的情况，就在原网格的基础上细划局部网格，如图3 所示。

图3 有限元局部细化网格后的弹靶模型

复合材料在受到弹丸冲击的过程中，从接触到结束的时间很短，弹丸侵彻靶板的过程如图4 所示。

图4 弹丸侵彻靶板的过程

在整个冲击过程中，先出现高速区，当拉伸波产生的应力超过材料的抗拉强度极限（Sc）时，材料易产生裂纹。随着过程的进行，弹丸的速度迅速下降，裂纹的扩展速率也开始下降。直到应力强度趋于0 MPa，裂纹的扩展速率Sc也趋于0。传统的有限元模拟采用局部网格细划，无法确切模拟高速冲击过程中的奇异点（此处不存在导数的解）。近场动力学理论采用的是微分-积分求解公式，能够克服在断裂处不存在导数的问题，其模型不再将材料中每个物质粒的移动看作独立的粒子移动，而是相对领域的粒子间形成的向量的相对位移量及向量两端力态的乘积，在近场动力学理论的公式中使用的是位移而不是位移导数，采用可应用于不连续体的空间积分方程。

最初，近场动力学理论的“键”基 PD 模型和“态”基PD 模型的理论都基于低速（v≤200 m/s）冲击试验，弹靶相互作用的冲击破坏的过程快且复杂，模拟裂纹萌生和扩展机理的难度很大。为了解决速度高于300 m/s 的冲击问题（尤其是构建冲击模型的问题），2010 年Silling 博士引入“双重状态”的概念[2-6]，将“态”近场动力学理论扩展到有限的区域内：成对质子相互作用和质子之间的间接相互作用对其他质子的影响，因此在分析复杂的多裂纹扩展的过程中，可以模拟和分析具有复杂破坏机理和多裂纹共存的不连续问题。在实际应用中，通过设置不同的材料属性参数能够更好地以积分形式重构高速冲击下，由各类同向性或异向性的材料粘合的连续体复合材料的运动方程，可以获得冲击荷载下质子跨界面运动及跨界面区域中质子的运动轨迹的整个过程（连续的过程）。

在PD 模型本构关系中，可以将材料看作是由无限物质粒构成的。材料发生形变有很多原因，此处的PD 模型中，当单看材料应力形变时，物质粒变形前到变形后的位移与紧接的下次位移是断裂开的，在相对领域内，材料的形变可以看作是物质粒间的非线性连续变化。基于非局部连续介质力学的近场动力学理论， 单质材料（例如钢板）可以理想化为二维PD 模型，单层厚度不同“三明治”复合材料的每层都可以设定独自的材料参数，当理想化为二维结构时，从厚度方向上就可以离散成单层的粒子，二维粒子模型（如图5（a）所示），粒子间的间距为Δx。如果理想化为三维模型（如图5（b）所示），那么其PD 的运动模型可以将复合材料看作不同材料层内单个领域（Hx）内质子的数量、位移的变化，在总体上可以看作多个领域Hx组成的整体，模拟的效果更接近试验的预期结果。

图5 PD 模型及非局部作用Hx 领域和子域

假设取整体复合材料中域H（xHx内包括多个间距为Δx的质子和作用域半径为δ构成的子域，如图5（c）所示），随着时间的变化，单质子运动产生的位移建立PD 本构关系还需要考虑近场动力学理论中的运动（平衡）方程，如公式（2）所示[3-9]。

式中：ρ为密度；u为位移；b为体力密度；T为位置和时间的函数；x为位置；t为时间；X和X'为相互作用的2 个质子。

在公式（2）中，T[X，t]〈X'-X〉为在以质子X为中心半径δ的子域内质子X′对质子X的作用；T[X，t]〈X'-X〉为在以质子X′为中心半径δ子域内质子X对质子X′的作用。因此，PD 运动方程的质子拉格朗日方程如公式（3）所示。

式中：T[X（k），t]〈X（j）-X（k）〉为t时间X（k）的力密度矢量T（k）（j）；T[X（k），t]〈X（j）-X（k）〉为X（j）的力密度矢量T（j）（k）；v（j）为每个质子的体积修正因子；b（k）为体积力密度矢量。

常见的“三明治”形式的多层复合材料由表面包覆层、阻燃胶、防弹层以及背板组成，如图6 所示。

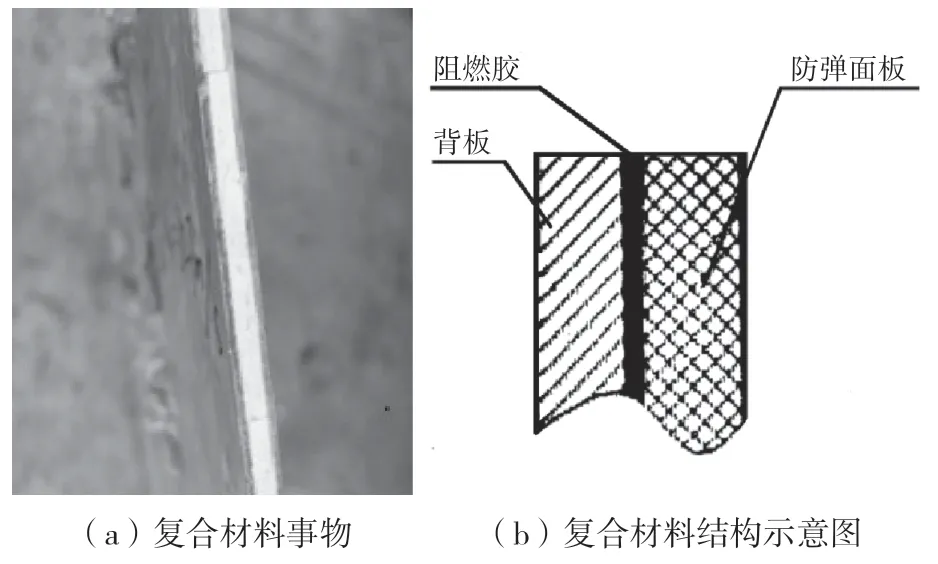
图6 多层复合材料

PD 模型Hx领域的粒子化如图7（a）所示。当Hx领域受到高速冲击时，粒子化的多层复合结构的材料在PD模型中粒子可以PD 的质子，其质子运动轨迹如图7（b）所示。

图7 材料粒子化

当进行PD 模型运算时，复合结构的材料的总厚度h如公式（4）所示。

式中：N为总层数；hn为第n层的厚度。

当受到高速冲击时，PD 模型的计算过程是将多层复合材料承载的外载荷以体力密度（单位体积的物质所受的力）的形式施加在临界材料边界上的非零体积真实材料层上，对相邻边界层R1表面S1上的分布压力p（x，t）或集中力P（t）的外载荷来说，它们的体力密度矢量b（x，t）如公式（5）所示。

最终，采用粒子离散方法建立近场动力学PD 模型，当模拟受到冲击时，受力粒子的运动轨迹如图7（b）所示，图中是由3 种不同物质材料复合而成“三明治”结构。

在近场动力学中，材料损伤是通过质点之间的相互作用（微势能）的截断来描述的。当2 个质点x（k）和x（j）之间的伸长率s（k）（j）超过它受力的临界值sc时，就会产生损伤。当出现损伤时，运动方程中2 个质点之间的作用力将不可逆的永久消失。质子对受冲击的裂隙尖的形成、裂缝的扩展以及边界效应、材料崩落的形式来说，非连续的物质的质子位移向量和端点矢量力都是动态的、连续变化的，避免了基于连续性假设建模和求解空间微分方程的传统宏观方法在面临不连续问题时的奇异性。因此，当通过计算收敛速度估算近场动力学微分时，可以用公式（1）作为模拟计算停止的判断准则。

模拟计算中近场动力学理论的运动（平衡）方程可以通过Taylor 级数展开近场动力学函数gp N（ξ），如公式（6）所示。

式中：ap q为a 展开的级数为p、项数q（a为多项式展开中的系数）；ω（ξ）为权函数；ξq为ξ展开q项。

权函数ω（ξ）指影响半径内控制相互作用的程度。根据Δx，权函数被指定为ω（ξ）=Ae-（ξ/δ）2或ω（ξ）=1，其中ξ=|x（j）-x（k）|，影响半径通常被指定为δ=mΔx（δ为影响半径）。

影响动力学微分与局部精确微分的偏差的因素除了权函数ω（ξ）外，还有其相互作用的域Hx、近场动力学函数gNp（ξ）的项数以及Taylor 级数展开式的剩余项R（N，x）。

在实弹试验的过程中，随着海拔高度的变化，大气压力、温度对弹道参数影响较大，对影响试验结果与依靠射表计算的预期结果之间的偏差影响的因素如下： 1） 空气阻力Rx（如公式（7）所示）。2） 阻力系数Cx0（M）（如公式（8）所示）。

式中：ρ为气体（或流体）密度；v为气流速度；S为弹丸横截面积；M为马赫数；Cxj为模组系数；Cxb为涡阻系数（或地主系数）；Cxw为波阻系数。

与枪弹相比，当炮弹飞行时，其空气在弹丸表面形成附面层，由外到内分别为边界层、层流附面层和紊流附面层，计算过程还应考虑影响炮弹弹速、着弹点的因素——雷诺数（附面层由层流向紊流转变的因子），如公式（9）所示。

式中：l为弹长，有时也可以用弹丸的直径表示；η为气体的黏性系数。

空气的黏性系数与高度或温度的经验公式如公式（10）所示。

式中：τ为按温度随高度分布的标准定律，τ=τ（y）（y为高度）。

为了简化计算过程，海拔高度的变化对弹道参数的影响因素作为约束条件可以设置为常数，也可以设置为输入项。当应用微分算子运算规则求解微分-积分时，可以放宽连续性假设条件，近场动力学的微分算子对函数进行泰勒展开，其等价公式如公式（11）所示。

式中：f（x）和f（x+ξ）为求微分的目标函数（ξ是x的增量）；p为阶数；g为近场动力学函数；f为求微分的目标函数；gNp为函数g展开的级数为p、项数为N。

公式（11）可以把具有p阶连续性要求的目标函数f（x）的微分运算等效为将目标函数f（x+ξ）乘以一个特定的近场动力学函数g的积分运算来求解，利用这种解析方法来求解PD 运动方程的质子拉格朗日方程（公式（3））。

随着中印边界问题的凸显，对武器装备在不同海拔的实际防护能力的研究日益迫切。在不同海拔高度的实弹试验过程中，会受到许多条件的限制（随着海拔高度的变化，影响弹丸速度、着靶和威力等性能的条件（例如大气压、温度等）也会发生变化）。依靠现代计算机运算的强大功能，合理选择、利用数值计算的理论方法，根据给出的测度值和需求条件计算，高速冲击对目标体的运动过程及结果，与选定的特定海拔试验得出的数据进行对比，可以得到更准确的研究资料。

利用近场动力理论对作用域的积分求解可以避免有限元方法对导数求解的奇异性，可以更准确地模拟高速冲击对目标体的运动过程。计算近场动力学代码包括时间步长、最小时间步长、递增时间、迭代次数、初始条件边界条件的设定、域内面力以及界面修正补偿（多种复合材料粒子化材料边界的非完整粒子的修正）的非线性的求解。

二维PD 模型计算量与同材料的有限元的计算量近似，在裂纹自然形成的模拟计算中，二维PD 模型比有限元模型精确，其原因是2 种模型的计算方法不同。

三维PD 模型计算量非常大，但是非常态基的近场动力学分模块化计算的方式与现代计算机的并行结构更匹配，PD 模型的可分解成多模块的结构适用于多点触发的并行计算模式（多路处理器并行处理的计算机），与二维PD模型相比，其更能体现多路处理器的计算机优势，既能节约计算时间，又能很好地模拟材料的动态、连续变化。

4 结语

弹丸侵彻形成了对多层复合材料的高速冲击，时间短且速度快。弹丸和多层复合材料之间相互作用的动作复杂、过程暂短，很难捕捉材料从变形、裂隙出现和裂纹扩展的活动过程。基于非局部作用思想建立的近场动力学理论是国际上兴起的、适用于模拟材料的损伤和断裂过程的理论。该理论通过求解基于时间和位移的空间积分的运动方程，重现高速冲击下多层材料物质粒的活动，避免了基于连续性假设建模和求解空间微分方程的传统宏观方法在面临不连续问题时的奇异性。Silling 博士于2000 年首次提出近场动力学理论，突破了经典分子动力学方法在计算尺度上的局限性，对宏观、微观不连续力学问题进行分析，包括均匀与非均匀材料的结构变形、损伤、断裂、冲击、穿透和失稳问题。至今，近场动力学理论的研究范围已经扩展至结晶相变动力学问题以及纳米材料和结构的破坏问题。研究的材料和结构已涉及金属、混凝土、多种复合材料、层合板结构、玻璃、颗粒材料、木材以及纳米纤维结构等。

在实际工程中，近场动力学理论为破坏机理的研究提供了强有力的解决理论基础。作为一种非局部理论，近场动力学避免了传统方法在解决不连续问题过程中存在的奇异性，成为研究脆性材料破坏行为的一种新兴研究理论，在研究弹丸高速冲击下，近场动力学在复合材料损伤方面具有以下3 个特点： 1） 与经典连续介质力学不同，近场动力学是采用积分方程而不是位移分量的导数来表示的。近场动力学允许材料内部自发的裂纹萌生与扩展路径自由，不需要引入额外的裂纹扩展准则。在近场动力学理论中，内力是由连续体中任意2 个物质点之间的本构关系来表示的，损伤是本构模型的一部分。2） 近场动力学理论研究基于有限的区域内质子间的相对位移和相互作用，结合物质离散粒子理论，以积分形式重构高速冲击下连续体的运动方程，允许位移场不连续，在处理不连续问题的过程中有数值优势，可以更好地解决不同物质黏合后在冲击荷载下质子跨界面运动及跨界面区域中质子的运动轨迹的连续性问题。3） 近场动力学的PD 计算模型的无网格架构非常适合进行并行计算，根据使用的处理器数量，并行计算可显著提高计算效率。