融合多尺度自注意力机制的运动想象信号解析

刘 京，赵 薇，董泽浩，王少华，王 余

1.河北师范大学计算机与网络空间安全学院，石家庄050024

2.河北师范大学软件学院，石家庄050024

3.河北师范大学数学科学学院，石家庄050024

脑电图（electroencephalogram，EEG）是由Hans Berger 于1924 年首先检测到并命名，是测量电极和基准参考电极所采集得到电位的差值，是两个电极间大量神经元自发性、节律性放电的电位差的记录。EEG由于其简单、安全和低廉的优势而被广泛用于许多非侵入性脑机接口（brain-computer interface，BCI）系统的研究中[1]。BCI通过脑电信号和解码技术在人脑和计算机之间建立直接通路。早期的BCI 系统主要用于中风康复或改善残疾患者的生活质量，如控制电动轮椅[2]、文字拼写器[3]和假肢[4]等。近些年，BCI系统不仅仅局限于残疾患者，还被广泛应用于健康人群[5]。在不同类型的EEG信号中，运动想象（motor imagery，MI）脑电信号作为一种经典范例已经研究和开发了数十年。其生理学基础是，当人们用双手、双脚或舌头想象或执行动作时，在脑半球的对侧和同侧的感觉运动区域中，mu（8～12 Hz）和beta（16～26 Hz）节律的能量受到抑制或促进，即产生事件相关同步/去同步（ERS/ERD）现象[6]。

BCI 的关键问题是如何实现脑电信号的精确分类，尽管学者们在MI分类方面提出了许多方法，包括机器学习的方法和深度学习的方法，但是仍然面临着许多挑战。首先，之前的方法主要选择在感觉运动区域的电极（如C3、Cz、C4电极）记录的脑电信号，但不同身体部位的MI可能会激活大脑的不同功能区域[7]，所有的大脑功能区域都会对不同的MI 任务产生一定的影响，而不仅仅是感觉运动区域。由于MIEEG 信号活动的幅值与响应时间因人而异，无法确定哪个脑区与MI 最相关[8]。其次，MI 信号在时间上是连续的，具有低信噪比（signal-to-noise ratio，SNR）的特性，并且容易受到多种生物学因素（如眨眼、心脏跳动和肌肉活动产生的眼电、心电和肌电）或环境伪影（如机器的工频噪声）的影响。这些目前面临的挑战的组合使得以前的方法提取特征的能力有限，并且分类准确率较低。

为了克服如上问题，本文提出了一种基于注意力机制的多尺度时空自注意力网络模型，用于原始MI-EEG信号的运动想象任务分类，该模型由特征提取模块、特征融合模块与特征分类模块组成。本文方法假设在大脑活动过程中，与运动想象相关的通道应分配更高的权重值。权重值根据本文提出的空间自注意力机制计算得到，该机制捕获高级可区分的空间特征，并在原始MI-EEG信号数据的空间域中定义更紧凑、更集中的表现形式。MI-EEG信号是一种非平稳时序信号，可以采用时间卷积神经网络（temporal convolutional neural networks，TCN）提取EEG信号随时间变化的状态和程度，且TCN 可以通过扩张卷积和改变卷积核大小的方式来保证浅层网络获得更大的感受野，同时其反向传播路径与序列的时间方向不同，因此TCN 在一定程度上可以避免梯度消失和爆炸的问题。本文在TCN 网络架构的基础上，采用并行多尺度TCN 层，以解决MI-EEG 信号中时间域上存在的噪声干扰的问题，同时可以提取不同尺度的时间域特征信息，与空间自注意力机制得到的空间域特征信息相结合，得到丰富的时空域特征信息，进一步提高分类性能。本文的主要工作如下：

（1）在空间域中，本文使用空间自注意力机制层提取任意两个通道的脑电信号之间的潜在空间联系。某一通道的特征通过加权求和的方式聚合所有通道上的特征来更新，其中的权重是通过相应通道之间的特征相似性计算得到的。定义了一种新的原始MI-EEG信号空间域特征信息的表示形式，通过自动分配较高的值给运动相关的通道，较低的值给运动无关的通道来选择最佳的通道。该层提高了分类精度，消除了人工选择信号通道所产生的特征信息的丢失。

（2）在时间域中，MI-EEG 信号是连续的时序信号，具有信噪比低的特性，从原始脑电信号中提取与MI 相关的特征信息相对困难。因此，本文使用并行多尺度TCN 层消除时间域特征信息中的噪声，并利用不同时间尺度的TCN网络提取不同尺度下的时间域特征信息。

（3）将两层得到的特征图拼接融合，得到MIEEG空间域与时间域特征信息增强的特征图。为了验证所提出模型的性能，将该模型在三个公共数据集上进行了评估。相应结果表明，本文方法在MI-EEG的分类任务上优于几种传统方法（平均提高11.84%），与基于DL 的方法相比，本文方法也处于领先水平。为了直观地从生理上验证所提出的空间自注意力机制的合理性，本文绘制了MI-EEG 数据的脑地形图，据此来说明MI 不仅激活了C3、C4、Cz 通道，而且还影响了其他的通道。

1 相关工作

针对MI-EEG 信号的分类已有许多研究。这些研究可以分为两类：传统研究方法和基于深度学习的方法。在传统研究方法中，共空间模式（common spatial pattern，CSP）算法[9]及其变体，如滤波器组共空间模式（filter bank common spatial pattern，FBCSP）[10]，被广泛用于从多通道EEG数据中提取特征的空间分布。Jin 等人[11]使用Pearson 的相关系数手动选择包含最相关信息的通道，然后使用正则化的共空间模式（regularized common spatial pattern，RCSP）提取有效特征，并使用支持向量机（support vector machine，SVM）作为分类器。但是，特征选择工程在很大程度上取决于手工特征的选择，依赖于人类的经验。此外，由于MI-EEG具有有限的空间分布，易受噪声干扰，信噪比（signal-to-noise ratio，SNR）低和随时间发生变化的高动态特性，传统方法无法实现高精度解码。

目前，深度学习（deep learning，DL）在各个领域中均表现出优越的性能，尤其是在计算机视觉、自然语言处理和语音识别方面取得了巨大成就，在各种医学应用中也表现出卓越的性能[12-14]。DL 的发展引起了BCI 领域研究人员的关注。相关研究包括基于深度学习模型的脑电特征提取[15]、癫痫病的预测和监测[16-17]、分类[18-19]和听觉音乐检索[20]。

深度学习在基于MI-BCI系统的分类任务中发展迅速，根据网络的输入形式，基于DL 的MI 分为两类：特征输入网络和原始信号输入网络。特征输入网络的MI脑电信号分类分两个阶段完成。首先，通过传统的特征提取方法，如功率谱分析、小波变换和CSP 等，将MI-EEG 信号的空间、频谱和时间信息组合在一起，将1D 的特征向量人工转换为2D 的特征图。然后，将这些特征图输入网络，采用DL 训练模型对特征进行分类。Bashivan等人[18]将MI-EEG信号转换为保留拓扑的多光谱图像，并训练了一个深度递归卷积神经网络来进行分类。Kumar 等人[12]使用CSP 提取特征，然后将其输入到多层感知器（multilayer perceptrons，MLPs）中。Tabar 和Halici[21]将通过短时傅里叶变换生成的时频特征图输入具有5层堆叠式自动编码器的CNN（convolutional neural networks）中进行分类，取得了很好的结果。Sakhavi等人[22]提出了一种新的特征表示方法，该方法结合了FBCSP 和Hilbert变换来提取空间域和时间域特征，随后将特征输入到5层的CNN网络中进行分类。Zhu等人[23]提出了一种分离通道的卷积神经网络对多通道的MIEEG 数据进行编码，将编码后的特征拼接起来输入到识别网络中，来执行最终的MI分类任务。

另外一种输入形式是将原始时间序列MI-EEG信号（即C（通道）×T（时间点）矩阵）直接输入DL神经网络中，该方法无需人工选择特征即可从原始EEG 信号中获得高级隐式特征，是一种端到端的方法。目前已经提出了几种性能较好的端到端DL 模型。受到FBCSP 的启发，Schirrmeister 等人[24]提出了ShallowNet和DeepNet两种卷积神经网络，与FBCSP相比，两者均具有更高的精度。EEGNet[19]是一个通用型的EEG 任务分类网络，它使用相对较少的参数在不同的EEG分类任务上实现了良好的性能。Azab等人[25]提出了一种新的加权迁移学习的方法，提高了MI-BCI系统分类的准确率。Song等人[26]通过将表示模块、分类模块和重构模块组合到端到端框架中，利用有限的MI-EEG 数据提高了分类性能。Li 等人[27]提出了一种通道投影混合尺度卷积神经网络架构，采用扩张卷积的方法扩大感受野，来提取不同尺度下的时间域特征，提高了分类性能。Amin 等人[28]采用一种用于融合具有不同特征和架构的多层CNN方法，利用不同的卷积网络从原始MI-EEG信号中提取空间域和时间域特征。Wu等人[29]提出了一种并行的多尺度滤波器组卷积神经网络的方法，通过不同尺度的卷积核来提取不同尺度下的原始MI-EEG 信号时间域特征，从而提高分类精度。Ingolfsson 等人[30]首次将TCN 应用于MI-EEG 分类任务中，取得了很好的结果。

两种输入形式都有其优点和缺点。特征输入网络的方法由于是人工选择特征，具有强大的可解释性，适用于小型数据集，并且优于传统方法。但是，人工选择的特征会丢失一些潜在的信息，从而影响性能。而端到端模型可以从原始MI-EEG 信号数据中自动学习有用的潜在信息，并可以获得令人满意的结果。但是，对于小的训练数据集，端到端的方法很难训练出令人满意的模型。从文献中可以看出，为MI-EEG 分类设计可行的端到端深度神经体系结构仍然是一个挑战。

2 本文方法

本文的网络体系结构如图1所示。图中，平行四边形是不同层中的特征图，它们对应的大小在四边形周围标明。Ⅰ是特征提取层，其中空间自注意力机制层与并行多尺度TCN 层由橙色和蓝色方块表示；Ⅱ是特征融合层；Ⅲ是特征分类层。D为特征图的个数，H为特征图的高度，W为特征图的宽度。输入的运动想象原始信号M为22个采样通道，1 125个时间采样点。网络架构分为三个模块：特征提取模块、特征融合模块、特征分类模块。

图1 所提方法的网络结构示意图Fig. 1 Schematic diagram of proposed method

首先介绍特征提取模块，该模块包含平行的空间自注意力层与并行多尺度TCN 层两层，在空间域和时间域提取可区分的特征；然后介绍特征融合模块，该层将特征提取模块得到的两组特征图进行拼接融合；最后将得到的特征图输入到特征分类模块中进行分类。

2.1 特征提取模块

2.1.1 空间自注意力层

传统方法通常是人工手动选择EEG 通道，或者假设每个通道都起着同等的作用。然而，不同的人对于相同的MI动作的脑活动区域是不同的，这就意味着不同被试的MI信号的强度是不同的，同样的被试在不同的试验中MI信号的强度也存在差异。这种现象会导致较低的分类精度。因此，为了消除人工选择信号通道造成的损失，本文提出了空间自注意力层，自动选择最有用的信号通道来提取被试者的判别特征。

该层的相应网络架构如图2（其中M∈RH×W表示原始信号数据，A∈RD×H×W表示卷积之后得到的特征图，D为特征图的个数，H为特征图的高度，W为特征图的宽度。C、E表示重塑之后的特征图，用于计算通道间的相似性。⊗表示矩阵乘法，⊕表示逐元素求和）所示，网络参数如表1所示。由图1，M∈RH×W为高度H=22 和宽度W=1 125 的运动想象脑电信号原始数据。首先将这些数据输入一个卷积层（Conv11）得到特征图A，其中A∈RD×H×W，D=8 表示特征图的数量。由图2，将A重塑为C∈RH×(D×W)和E∈R(D×W)×H，用来实现它们之间的矩阵乘法。最后，应用Softmax 函数得出空间自注意力权重矩阵P∈RH×H，相应公式如下式所示：

表1 空间自注意力机制层网络的详细说明Table 1 Detailed architecture of channel self-attention mechanism module network

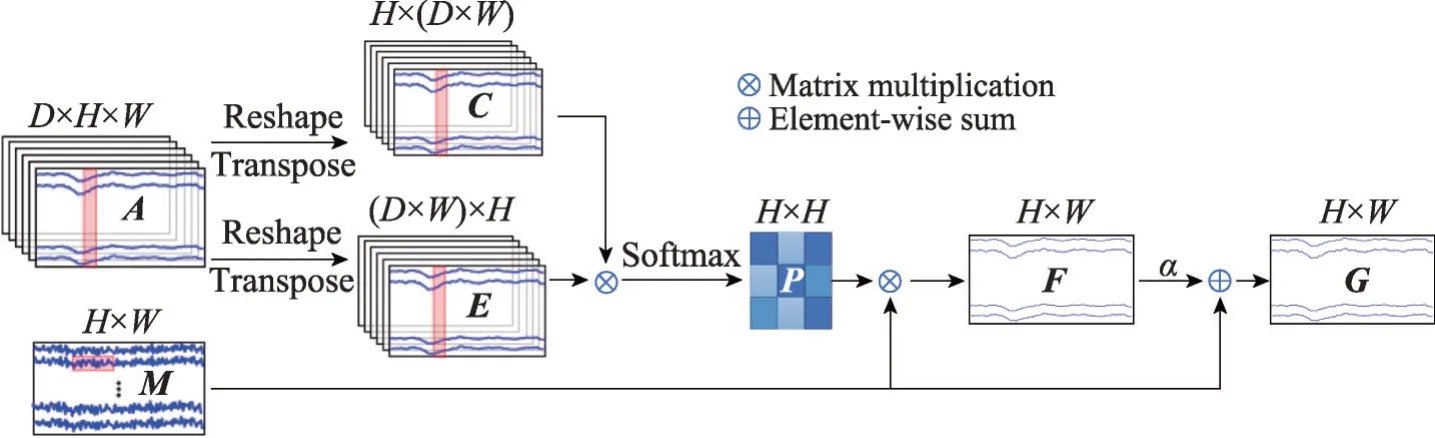
图2 空间自注意力机制层网络结构示意图Fig. 2 Schematic diagram of channel self-attention mechanism module network

式中，f是相似性函数，使用矩阵点乘来计算相似度。P表示相似度，表示第i个通道和第j个通道的相似性，取值范围为0～1（0 表示没有相似性，而1 表示完全相似）。

之后由式（1）得到的P与M∈RH×W矩阵乘法来获得信号F∈RH×W。信号F是通道预测信号，其中每个通道都是原始数据空间域中其他通道的加权和。该工作自动学习通道之间相似的权值，自适应地集合所有通道的信号数据，并使用加权求和来更新每个通道。最后，本文通过将F与可学习的参数α相乘形成一个残差块，并对原始信号执行逐元素求和运算，获得最终的空间特征信号G∈RH×W，相应公式如下：

其中，α初始化为0，并在整个深度学习模型的训练过程中逐渐更新被分配更合适的权重。G增强了跨被试分类的性能。这意味着当人们思考一个动作时，任何具有相似特征的通道都能相互促进，而不管它在大脑中的空间位置。

2.1.2 多尺度TCN层

MI-EEG 信号在时间域上具有连续且SNR 低的特性。因此，本文构建了一个多尺度TCN 层，利用TCN能够并行处理和增大感受野且一定程度上能够避免梯度消失与爆炸的优势，采用不同的时间步长提取不同尺度的时间域特征信息，再将这些特征拼接融合，得到增强的时间域特征信息，同时消除噪声影响，增加鲁棒性，提高分类性能。该层的相应网络架构如图3，网络参数如表2所示。

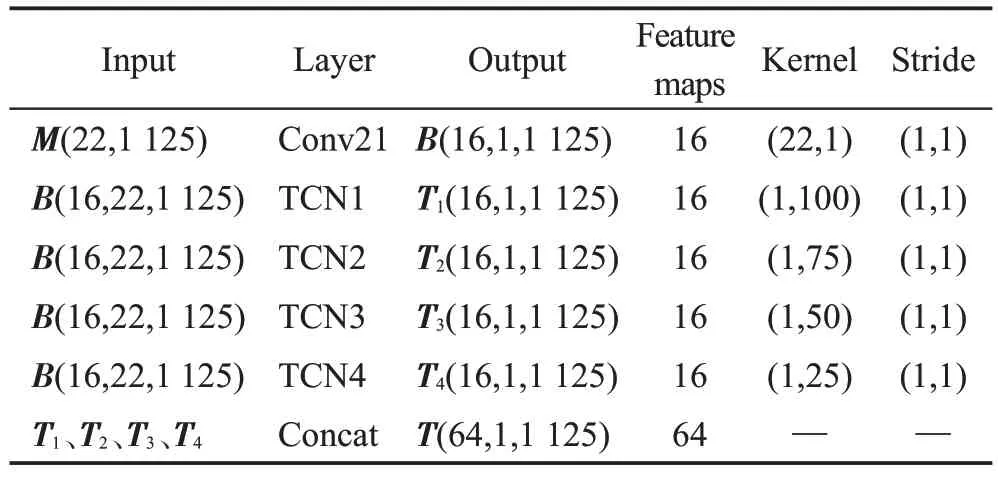
表2 多尺度TCN层网络的详细说明Table 2 Detailed architecture of multi-scale TCN module network

图3 多尺度TCN层网络结构示意图Fig. 3 Schematic diagram of multi-scale TCN module network

由图1，将M∈RH×W输入一个卷积层（Conv21）得到特征图B∈RD×1×W，Conv21的卷积核大小为（22×1），此时特征图B有16个，每个特征图大小为（1,1 125）。如图2，将特征图B并行输入4个不同尺度的TCN卷积层，每层TCN 的尺度由卷积核的大小体现。每层卷积核大小分别为（1×25）、（1×50）、（1×75）、（1×100），分别代表以100 ms、200 ms、300 ms、400 ms 的时间步长对MI-EEG特征图进行卷积，得到4组时间特征图T1,T2,T3,T4∈RD×1×W。其中，每层TCN 由若干个残差块组成，残差块的网络结构如图4 所示，其中卷积核大小KT=2，膨胀系数d={1,2}。

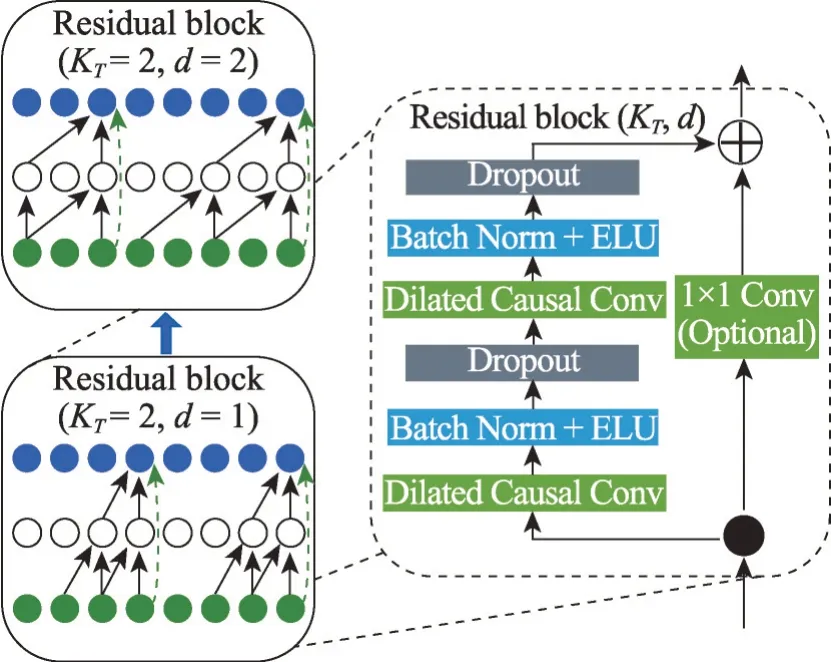
图4 TCN中的架构元素Fig. 4 Architectural elements in TCN

TCN[31]与常规CNN的区别主要是由于其三种结构：因果卷积、膨胀卷积和残差块[32]。

（1）因果卷积：TCN 的输出与输入的长度相同。为此，TCN使用1D全卷积网络架构[33]，其中每个隐藏层的大小与输入层的大小相同，采用0填充的方式使后续层的长度与先前层相同。此外，因果卷积保证没有信息从未来流向过去，简而言之，时间t的输入仅取决于时间t或更早的输入。

（2）膨胀卷积：常规的因果卷积只能在网络深度上线性增加其感受野大小，导致如果要获得大的感受野大小，就需要一个非常深的网络或者一个具有巨大卷积核的网络，这是常规因果卷积最主要的一个缺点。为了解决这个问题，TCN 使用一系列膨胀卷积[34]，该卷积通过成倍增加膨胀因子d的方法，使感受野的大小与网络深度成比例的方式增大。

（3）残差块：TCN 的残差块由两层膨胀卷积组成，每一层除了因果卷积层，还具有批量归一化、非线性激活和Dropout层。虽然TCN只有一维卷积，但将二维特征图的第二维度视为深度维，仍然能够处理二维深度图。跳过连接将输入添加到输出特征映射中，并检查输入和输出的深度是否相同，若不同，则会进行1×1卷积。

那么，膨胀基为b，卷积核大小k（k≥b），TCN的感受野大小l与残差块数n有：

在本网络中，b=2，l=W=1 125，则有：

k取值为25、50、75、100，则对应TCN 层的残差块数n为5、4、4、3，如图3所示。

最后，将4 组特征图T1,T2,T3,T4∈RD×1×W通过拼接函数融合为一组特征图T∈R4D×1×W，T即最终获得的消除噪声且包含不同时间尺度信息的时间域特征图。

2.2 特征融合模块

本节将空间自注意力层的输出G∈RH×W经过一个卷积核大小为（22×1）的空间卷积层（Conv12）得到特征图S∈RD×1×W，然后将S∈RD×1×W与T∈R4D×1×W按照深度维进行拼接融合，得到增强的时空信息特征图N1∈R5D×1×W，其中D=16，W=1 125，方法如下：

该模块的网络架构如图1中的Ⅱ部分，参数如表3所示。

表3 特征融合模块的详细说明Table 3 Detailed architecture of feature fusion layer

2.3 特征分类模块

本节将特征融合模块得到的N1∈RD×1×W输入到特征分类模块中，该模块的网络架构如图1中的Ⅲ所示，网络参数如表4 所示。该模块包含两个卷积层（Conv3 和Conv4，都包含批量归一化与非线性激活层）、两个平均池化层（AvgP1 和AvgP2，都包含Dropout 层）、一个全卷积层（FC）和一个LogSoftmax函数。

表4 特征分类模块的详细说明Table 4 Detailed architecture of feature classification layer

将N1经过一个内核大小为（1×75）的卷积（Conv3），采用0填充的方法得到与N1同样大小的特征图，将得到的特征图应用批量归一化与非线性激活得到N2。将N2通过内核大小为（1×8）的平均池化层（AvgP1），将输入大小（80，1，1 125）减小到（80，1，140）输出得到N3。将N3经过一个内核大小为（1×25）的卷积（Conv4），采用0填充的方法得到与N3同样大小的特征图，将得到的特征图应用批量归一化与非线性激活得到N4。N4再通过一个内核大小为（1×8）的平均池化层（AvgP2），将输入大小（80，1，140）减小到（80，1，17）输出得到N5。将N5通过一个内核大小为（1×17）的全卷积层（FC），其输出的大小为N6（4，1，1）。最后，通过N6转换为4 个标签的条件概率，使用LogSoftmax函数执行四分类。

2.4 训练策略

对于四类MI 分类，将Pytorch 中的NLLoss 函数定义为损失函数[35]，使用Xavier算法初始化网络中的所有参数[24]，优化算法采用Adam算法[36]。BCICIV2a和BCICIV2b 数据集的学习率为0.000 1，而HGD 数据集的学习率为0.001，批次大小为32。

由于3 个数据集均将训练数据集和测试数据集清晰地划分出来，本节将训练数据集随机分为训练集（80%）和验证集（20%），所有测试数据集作为测试集。采用这种划分方式可以使用在计算机视觉领域开发的早期停止策略。当验证精度在预定时期内没有提高时，训练的第一阶段停止。然后，使用使验证数据集具有最高准确率的参数值，继续对训练和验证数据集进行训练。当验证数据集上的损失函数下降到与第一个训练阶段结束时的训练数据集的值相同时，训练结束。Dropout 层中的超参数以及批归一化层中的常数和权重衰减率分别设置为0.4、10-5和0.1。

3 实验结果与分析

为了验证提出的模型的性能和可行性，对3个数据集进行了一系列实验。单被试分类实验目的是验证本文的模型对单被试分类的性能。之后设计了跨被试迁移实验，来验证所提出方法的迁移能力。在跨被试实验中，其他被试（除目标被试）的脑电信号用来预先训练模型，然后将该模型作为初始权重对网络进行初始化，最后对目标被试进行测试实验。

3.1 数据集说明

在这项研究中，本文采用了3个广泛使用的公共MI-EEG数据集进行评估。它们之间的主要区别在于通道数量、试验数量、被试数量、任务类别和采样率。

第一个数据集是BCICIV2a[24]，该数据集记录了由9 位不同的被试执行的四类运动想象任务（左手、右手、双脚和舌头），采样率为250 Hz，共25 个通道（22 个脑电通道和3 个眼电通道），每个通道都经过0.5～100 Hz带通滤波器的预处理。对于每个被试者，在不同的日子里共记录了两个时间段（session）的脑电数据。每个session 包含6 个运行（run），中间有短暂的休息。一个run 包括48 个试验（4 种可能的类别各12 个），每个session 总共288 个试验（trial）。本文使用一个session 作为训练集，另一个session 用于测试分类器和评估性能。因此，训练集由第一个session的288个试验组成，而测试集由第二个session的288个试验组成。此外，每个试验都使用相同的时间窗[-0.5,4]（单位：s）提取22个脑电通道的运动想象信号。因此，在数据集中，显式分离了9个训练集和9个测试集。在子集中，每个类别有72 个trial，并未提供反馈。因此，去除3 个眼电通道信号后，每次试验获得22×1 125 个数据点。

第二个数据集是BCICIV2b[24]，该数据集包含了6个通道（3 个脑电通道和3 个眼电通道），记录了9 个不同的被试两类运动想象任务（左手、右手）。对于每个被试，运动想象任务分为5个session，BCICIV2b数据集中的前两个session 在运行时没有反馈，其余session具有反馈。

第三个数据集是HGD 数据集[24]，该数据集包含了44 个脑电通道，记录了14 位健康被试进行的4 类运动想象任务，对想象运动进行4 s 试验。每个被试包含13 个session，每个session 包括80 次试验。这4类运动包括左手、右手、双脚和休息（不动）。对于每个被试，训练集由大约880个试验（除了最后两个session 的其他session）组成，测试集由大约160 个试验（最后两个session）组成。HGD 的采样率为500 Hz。为了与BCICIV2a 进行公平的比较，对HGD 重新采样，采样率为250 Hz，并使用相同的4.5 s 时间窗，因此每个试验获得44×125 个数据点。

3.2 评估指标

本文方法在3个公共数据集BCICIV2a、BCICIV2b和HGD 上进行评估，以准确率作为评价指标。计算公式为：

其中，TP为真阳性数，TN为真阴性数，FP为假阳性数，FN为假阴性数。

3.3 单被试分类实验定量评价

3.3.1 BCICIV2a数据集的比较

为了验证提出方法的有效性和准确性，首先使用BCICIV2a进行了单被试分类实验，并将本文方法的准确率与基于DL 的方法EEGNet[19]、M3DCNN[37]、CPMixedNet[27]、MSFBCNN[29]、DMTLCNN[26]、MCCNN[28]、WTL[25]、EEG-TCNet[30]和基于ML 的方法FBCSP[10]进行比较，结果见表5（最优的准确率加粗显示）。

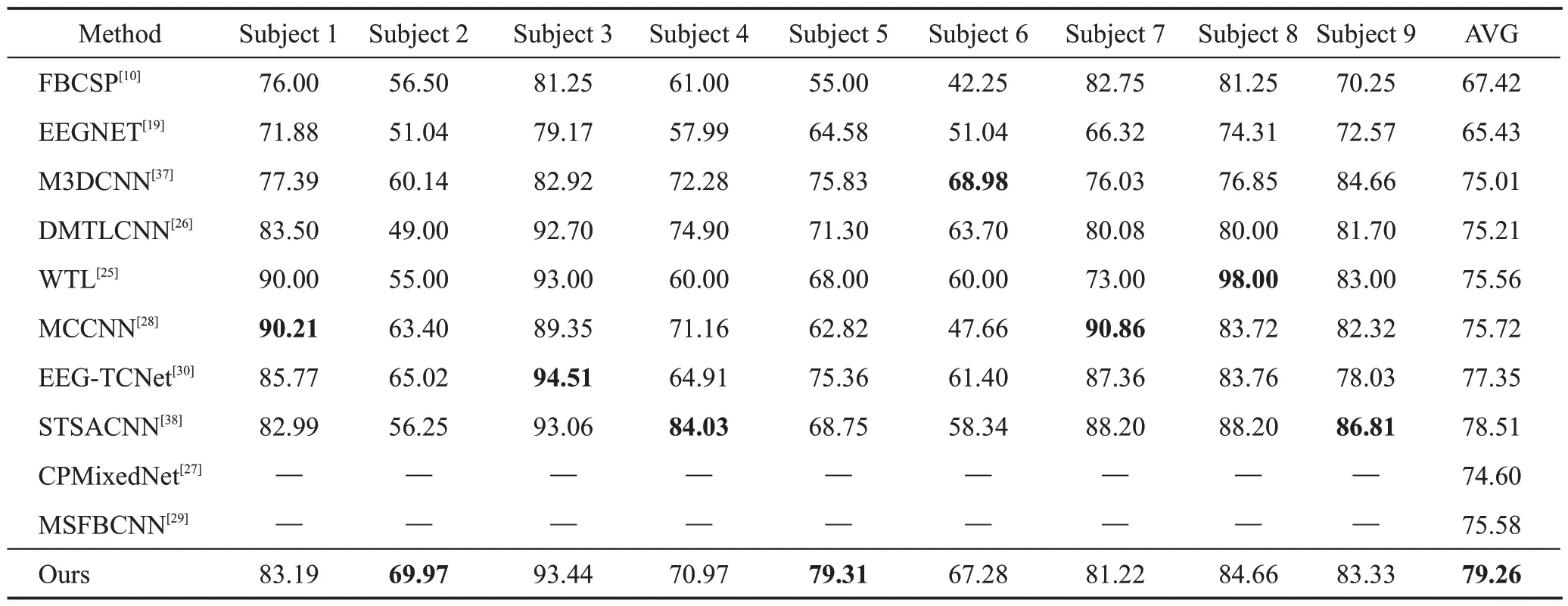
表5 BCICIV2a数据集在单被试分类中的准确率Table 5 Accuracy on BCICIV2a dataset for intra-subject classification 单位：%

表5 列出了各种方法中每个被试者的准确率以及BCICIV2a 数据集的平均准确率。本文方法明显优于其他基于DL的方法，对单被试分类的平均准确率为79.26%。此外，图5（a）中给出了MI任务的混淆矩阵和测试集上的实验结果。FBCSP 是一种基于ML 的基线方法，被广泛用于识别振荡的MI-EEG 数据，该方法使用支持向量机作为分类器。它选择最优的空间滤波器来提取特征，并且在BCI比赛中运行BCICIV2a时表现最好。但其在所有被试者中的平均准确率仅为67.42%，比本文方法低了11.84 个百分点。因此，与传统的机器学习方法相比，本文方法拥有更好的结果。

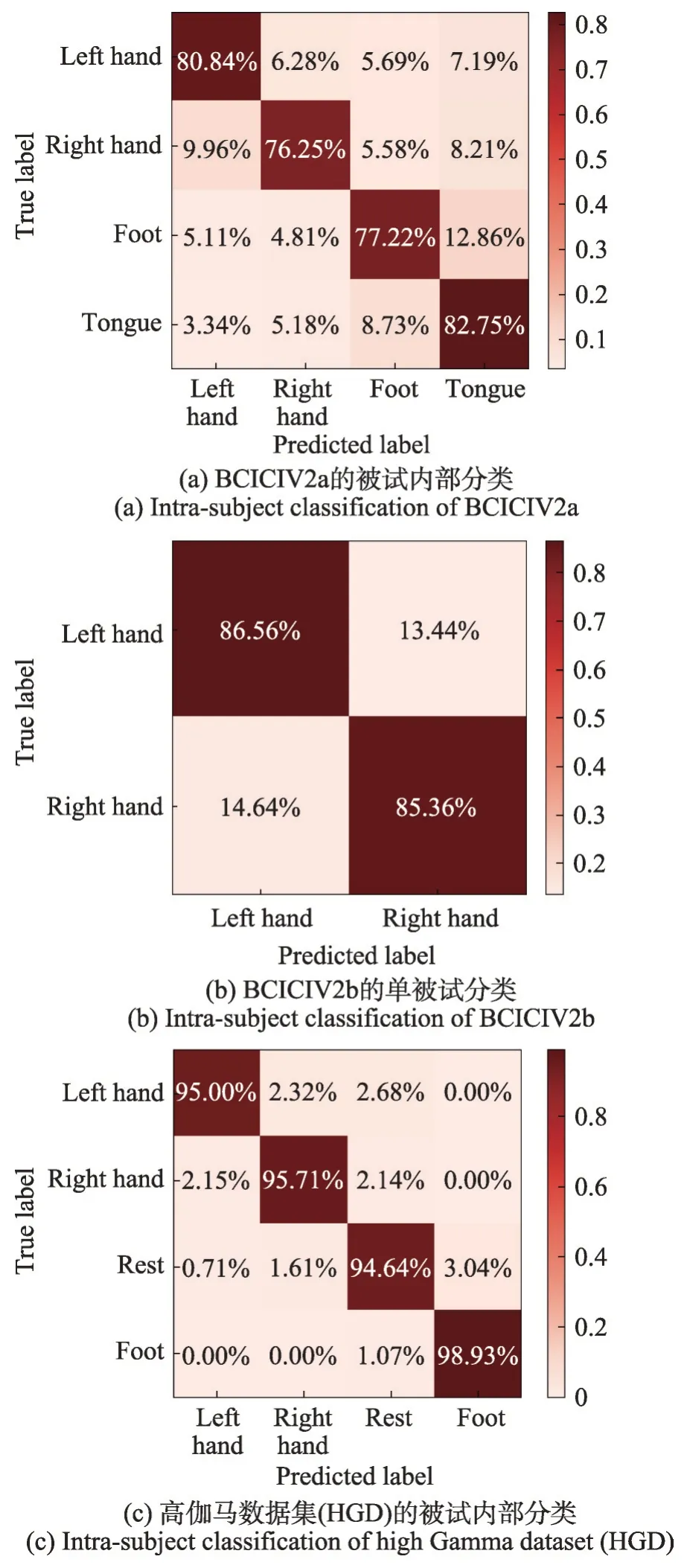
图5 运动想象（MI）任务的混淆矩阵Fig. 5 Confusion matrices for motor imagery(MI)task

这里介绍的其他基于DL 的方法是具有较高准确率的最新技术。在此任务中，它们的平均准确率值的范围是65.43%至77.35%。M3DCNN 模型结合了新的EEG三维表示形式，采用多分支三维CNN和相应的分类策略，来增强其对不同被试的抗过拟合能力。M3DCNN的最大贡献是证明原始MI-EEG的复杂表示形式可以帮助改善性能。但是，其准确率为75.01%，比本文方法低4.25个百分点。DMTLCNN和WTL 使用迁移学习技术使分类准确率显著提高，分别达到75.21%和75.56%。与这两种方法相比，本文方法准确率分别提高了4.05个百分点和3.70个百分点，MCCNN模型采用不同的滤波器大小和深度提取不同类型的时空特征，融合不同架构的CNN模块，提高MIEEG分类精度。吴等人提出的并行的MSFBCNN，利用特征提取网络从脑电数据中充分提取潜在的时空特征[29]。Li 等人提出的端到端的脑电解码框架采用原始多通道脑电数据作为输入，利用CPMixedNet 和振幅扰动数据增强技术来提高精度[27]。与上述模型相比，本文的平均准确率分别提高了3.54个百分点、3.68 个百分点和4.66 个百分点。EEG-TCNet 是一种端到端的DL模型，拥有一个空间卷积和一个时间卷积，之后输入到TCN网络中进行特征提取，最后由全卷积网络进行分类。该网络第一次将TCN网络应用于MI-EEG 分类领域，并取得很好的结果，可以证明TCN 适合于MI-EEG 的分类研究。但是该网络没有考虑到不同尺度的时间域特征信息。与EEG-TCNet方法相比，本文方法平均准确率高出1.91个百分点。

以上结果表明，对于4 类MI-EEG 分类，本文方法优于传统方法，平均提高11.84 个百分点。与目前最新的基于DL 的方法相比，本文方法在BCICIV2a数据集的单被试分类实验上取得了更好的结果。除了平均准确率外，本文也在两个被试者（被试2、被试5）上取得了最好的结果。

3.3.2 BCICIV2b和HGD数据集的比较

为了进一步验证所提出方法的自适应性和鲁棒性，本文对另外两个具有挑战性的数据集BCICIV2b和HGD（见3.1 节）进行单被试分类实验来评估提出的模型的性能，网络结构并未进行改动，其中对二分类数据集BCICIV2b进行实验时，LogSoftmax的输出分类为二分类。由于目前最先进的方法仅提供了BCICIV2b 和HGD 的平均精度值，在比较时，本文仅将平均精度分别列于表6和表7中（最优准确率加粗显示），相应的混淆矩阵如图5（b）、图5（c）所示。

表6 BCICIV2b数据集在单被试分类中的平均准确率Table 6 Average accuracy on BCICIV2b dataset for intra-subject classification 单位：%

表7 HGD数据集在单被试分类中的平均准确率Table 7 Average accuracy on HGD dataset for intra-subject classification 单位：%

表6 所列的数据表明，BCICIV2b 的结果与其他最先进的方法相比有了良好的改进。本文方法获得了85.90%的准确率，而次优方法MSFBCNN 获得了84.30%的准确率，准确率提高了近1.6个百分点。表7 数据表明，本文方法在HGD 的实验结果取得了显著的提高，达到了96.96%的准确率。实验结果表明，提出的网络模型对不同的脑电数据集及不同的分类任务具有较好的自适应性和鲁棒性。

3.4 BCICIV2a 数据集跨被试分类实验定量评价

为了验证所提出方法的迁移学习能力，本文进行了跨被试分类实验。本文采用迁移学习技术，利用其他被试（除目标被试）的脑电数据在BCICIV2a数据集上训练一个模型，然后将该模型作为网络的初始权值进行初始化，之后加载新被试者（目标被试）的数据进行进一步测试。这样，训练后的模型可以整合其他被试者的信息，从而使其更具鲁棒性。

表8 给出了每个被试者对应的分类结果（最优准确率加粗显示）。由于每个被试的MI-EEG活动的幅值和响应时间有差别，不同被试者之间差异较大，故而表8中的结果并不优于单被试者分类的结果（如表5所示）。图6为BCICIV2a数据集跨被试分类结果的混淆矩阵。与其他先进的DL 方法（仅DeepCNN、DMTLCNN、STSACNN 提供跨被试分类实验比较结果）相比，本文方法平均准确率为73.78%，9个被试者中2个被试（被试2、被试9）取得最优。

表8 BCICIV2a数据集上跨被试迁移学习分类结果Table 8 Results of inter-subject transfer learning classification on BCICIV2a dataset 单位：%

图6 MI任务的混淆矩阵（BCICIV2a跨被试分类）Fig. 6 Confusion matrices for MI task(inter-subject classification of BCICIV2a)

结果表明，本文方法不仅可以由网络自动学习与MI相关的通道信息，消除了手动选择信号通道的影响，同时为MI脑电信号的分类提供了更通用的特征表示，具有更好的鲁棒性和更高的分类准确率。

3.5 BCICIV2a数据集交叉验证实验定量评价

为了验证本文所提出的模型的预测性能和泛化能力，本文进行了10 倍交叉验证实验。在数据集有限的情况下，本文结合BCICIV2a 的训练集和测试集，每个被试者有576个试验，将它们随机分为10个相等的部分。每次运行使用9 个子集作为训练集，1个子集作为测试集，即518 个和58 个试验分别用于训练和测试。最终的准确率是通过取10次最佳值的平均值得到的。

表9 给出了10 倍交叉验证的结果（最优准确率加粗显示）。与本文之前使用的288个训练试验和288个测试试验相比，10倍交叉验证显著增加了训练集的数量，因此平均准确率提高了11.82%，达到了91.08%。除了平均准确率外，该数据集9名被试均取得最佳结果。这再次证明了数据量小确实是DL 方法的瓶颈。

表9 BCICIV2a数据集上使用十倍交叉验证单被试分类结果Table 9 Intra-subject classification of 10-fold cross-validation results on BCICIV2a dataset 单位：%

3.6 BCICIV2a数据集消融实验定量评价

为了验证所提出的空间自注意力层和多尺度TCN层的作用，本文进行了基于BCICIV2a的消融实验，该实验采用去除其中一层来测试另一层的作用，其中MSTCN-CAMNet 表示本文提出的网络结构，MSTCN 表示只包含多尺度TCN 层的网络结构，CAMNet 表示只包含空间自注意力层的网络结构。结果如表10所示。

表10 基于BCICIV2a数据集消融实验Table 10 Ablation experiments on BCICIV2a dataset

从表10 中数据可以看出，两层对所提出网络的准确率都有明显提升效果，验证了所提出两层的有效性。其中，对于空间自注意力机制层，多尺度TCN网络层对所提出方法的作用更大。

3.7 BCICIV2a数据集T-SNE实验定性评价

前几节进行了一系列定量评价任务，定量评价的标准为4 类MI 脑电分类准确率和混淆矩阵，混淆矩阵对角线上的值表示对每个运动想象分类任务的正确预测准确率。本节进行了t 分布随机邻域嵌入（T-SNE）定性评价任务。T-SNE 被广泛用于评价特征向量的判别能力，它可以将高维数据投影到二维散点图上。在T-SNE 可视化的情况下，评价标准如下：一个类的实例越多，可以从其他类的实例中分离出来，相关特征的表现就越好。本文所有的实验都在BCICIV2a上进行，使用相同的训练策略进行单被试分类实验。

如图7所示，被试者1的原始MI-EEG数据的所有类别标签均匀分布在T-SNE 图中。其中，数字0 到3代表MI-EEG信号的4类标签（左手、右手、脚和舌头）。

图7 被试者1在BCICIV2a原始数据上的T-SNE映射Fig. 7 T-SNE mapping of subject 1 on BCICIV2a raw data

被试者1的混淆矩阵及其对应的T-SNE图如图8所示。从图中可以看出，混淆矩阵中最大的误差发生在左手和右手之间以及脚和舌头之间。将脚分类为舌，错误率为23.04%，将舌头分类为脚，错误率为10.59%。这一趋势与图8的T-SNE图是一致的，在图8的T-SNE图中，误分程度最大的是label 2和label 3之间，对应的是脚和舌。从上面的实验可以表明，TSNE 图和相应的混淆矩阵具有相同的变化趋势：一个类的实例越多，可以从其他类的实例中分离出来，在四分类MI-EEG实验中获得更好的分类性能。

图8 被试1的混淆矩阵和相应的T-SNE映射Fig. 8 Confusion matrices and corresponding T-SNE mapping for subject 1

4 讨论

图9中（电极Cz位于头部的中心，C3、C4分别位于左右两侧。红色表示正相关，即表示幅值增加（ERD）；蓝色表示负相关，即表示幅值减少（ERS）），本文使用来自BCICIV2a 数据集的四类MI-EEG 信号，并画出与每个单被试分类结果相对应的大脑活动相关图。当人们想象或执行左手、右手、双脚和舌头运动时，mu（8～12 Hz）和beta（16～26 Hz）节律的能量会在大脑半球对侧和同侧的感觉运动区域减少或增加，即ERS/ERD 现象。因此，在图9 中本文将红色定义为表示ERD 的正相关，红色的色调越强烈，正相关性越强。将蓝色定义为表示ERS 的负相关，蓝色阴影越强烈，负相关性越强。例如，图9 中的第一行显示的是左手运动想象数据的大脑活动相关图。本文的分类结果是针对左手运动的MI-EEG 信号，相应的大脑活动相关图显示了左半球的ERS和右半球的ERD。

图9 BCICIV2a数据集上本文方法分类结果的大脑活动相关图Fig. 9 Brain active correlation map to classification results of proposed method on BCICIV2a dataset

图9 是在BCICIV2a 数据集上对四类MI 脑电信号进行分类，得到对应于本文方法分类结果的大脑活动相关图。图中所示的结果证明，当人们想象或执行某个动作时，任何具有相似特征的通道都能相互促进，而不管它在大脑中的空间位置如何。本文首次使用自注意力与TCN网络融合机制提取EEG信号的新时空特征表示形式，以提取可区分的时空特征。因此，从图9 中的图像中得出结论，本文方法在神经生理学上得到了可信赖的结果。

5 结束语

本文提出了一种基于注意力机制的多尺度时空自注意力网络模型，用于四类（左手、右手、双脚和舌头或休息）MI-EEG 分类。该模型由特征提取模块、特征融合模块、特征分类模块三个模块组成。其中特征提取模块由空间自注意力机制层和多尺度TCN层两个并行层组成，通过这两层可以提取到空间域和时间域上特征增强的可区分的时空特征。

本文使用三个公共数据集（BCICIV2a、BCICIV2b和HGD）进行实验，以验证本文方法对不同数据的鲁棒性和准确率。实验结果表明，本文方法与现有的基于DL 的方法相比，具有更好的分类性能，并且适用于单被试与跨被试实验，具有迁移学习的能力。同时，消融实验也证明了本文方法的有效性。未来，计划进一步完善模型，提高单被试与跨被试的分类性能。