桩板刚构桥设计与空间分析

程辉

（中铁上海设计院集团有限公司，上海 200070）

1 概况

某高速公路下穿高铁桥梁采用（20+25+20）m 桩板连续刚构桥，斜交角度62.6°，桥梁全长65m，设计荷载为公路-I 级。刚构桥单幅桥宽13.25m，上部结构采用等高度普通钢筋混凝土实心板，板厚1.2m，支点处加厚至2.2m，混凝土等级为C40。基础采用直径为1.2m钻孔灌注桩，基础与板固结，每排布置4 根，横向间距3.1m，混凝土等级为C30。

2 刚构分析方法及模型

2.1 分析方法

桥梁结构常用的分析方法是梁单元分析法。梁单元主要用来模拟具有明显受弯性质的细长构件，即构件轴向长度L 远大于截面的高度H 和宽度B(一般的判据为L/H>10,L/B>10)。梁单元理论采用的是平截面假定，即平截面为刚性平面，不能反映构件的横向变形、横向弯矩和纵向弯矩沿着横向的变化。本项目跨宽比（L/B=1.5<10）较小,在荷载作用下，结构呈双向受力状态，即除结构的纵向产生弯矩外，横向也产生较大弯矩，采用梁单元不能准确的反映结构受力状态，因此精确的结构受力需要采用板单元或实体单元进行空间分析。本文采用板单元进行结构分析，研究结构在荷载作用下的变形和弯矩分布趋势，提出此类结构的分析和配筋建议。

2.2 有限元模型

采用MIDAS-Civil 建立桩板刚构桥空间有限元分析模型，上部结构采用板单元模拟，桩基采用梁单元模拟，桩顶与对应的板单元节点设置刚臂连接。桩基按摩擦桩设计，桩基底按固结模拟。桩-土作用采用土弹簧法模拟，在每个桩单元的节点加入约束-双向受压弹簧，弹簧刚度根据“m”法计算。

3 计算结果及分析

本次研究主要考虑结构自重、二期恒载（桥面铺装和防撞护栏）、汽车活载、梯度升温荷载。防撞护栏和桥面铺装按照实际作用位置采用均布压力荷载进行布置，汽车荷载按车道实际位置进行加载，梯度温度荷载按照《公路桥涵设计通用规范》（JTG D60-2015）第4.3.12节规定加载。

3.1 竖向挠度计算

3.1.1 恒载挠度计算

由恒载作用下挠度图（如图1 所示）可以看出，恒载作用下边、中跨最大挠度均位于跨中位置。由于受结构斜交、弯扭耦合的影响，边跨跨中截面竖向挠度沿板宽方向分布表现出更为显著的空间变形特点，即锐角侧挠度大，最大挠度-10.3mm，钝角侧扰度小，最小扰度-5.7mm，两侧挠度差4.6mm，挠度差占平均挠度比57.5%，挠度沿板宽方向分布较不均匀。

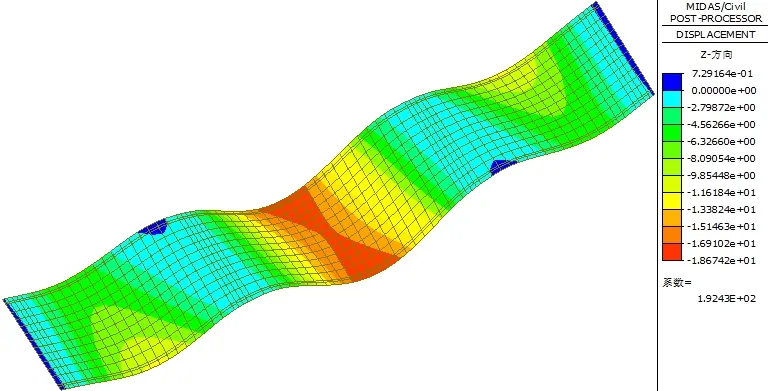
图1 恒载作用下挠度图 单位：mm

中跨跨中截面竖向挠度沿板宽方向呈“拱”形分布，即是两边缘挠度大，中间挠度小，边缘处最大挠度-18.6mm，板中央挠度-17.0mm，挠度差1.6mm，挠度差占平均挠度比8.9%，挠度沿板宽方向分布相对均匀。

3.1.2 活载竖向挠度计算

由活载作用下挠度图（如图2 所示）可以看出，活载作用下边、中跨最大挠度位于跨中。由于车道靠近锐角侧自由边偏载布置，活载作用下板挠度沿板宽分布不均匀，呈锐角侧挠度大，钝角侧挠度小的特点。边跨跨中锐角侧边缘最大扰度-1.4mm，钝角侧边缘挠度-1.0mm，挠度差0.4mm，挠度差占平均挠度比33.3%。

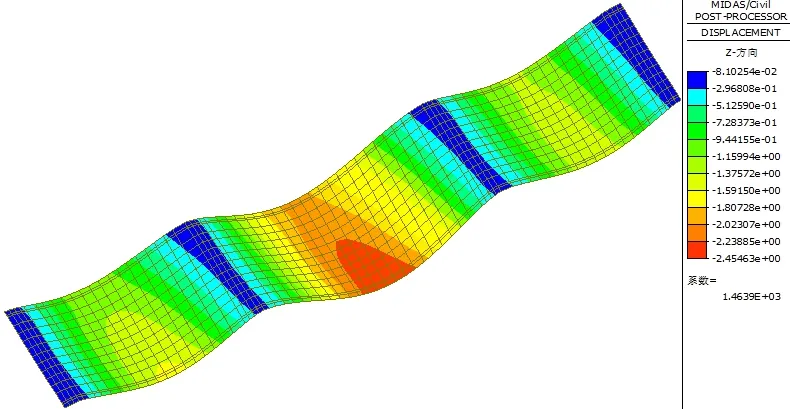
图2 活载作用下挠度图 单位：mm

中跨跨中锐角侧边缘最大扰度-2.4mm，钝角侧边缘挠度-2.0mm，两侧挠度差0.4mm，挠度差占平均挠度比18.2%。

3.1.3 梯度升温作用竖向挠度计算

由梯度升温作用下的挠度图（如图3 所示）可以看出，在梯度升温作用下，板的变形呈现出明显的空间变形特点，纵向发生弯曲同时，板横向弯曲成“拱”形，拱顶位于板的中线处，拱脚位于板的边缘。

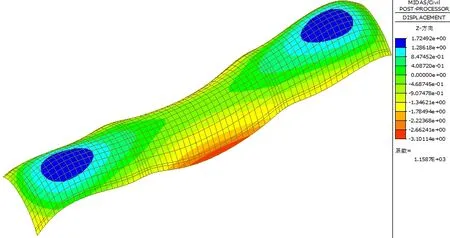
图3 梯度升温作用下的挠度图 单位：mm

边跨跨中截面在板中线处最大上拱1.72mm，边缘处下挠-1.1mm，挠度差2.82mm；中跨跨中截面在板中线处下挠-0.16mm，边缘处下挠-3.1mm，挠度差2.94mm。

由于板较宽，钝角侧边缘和锐角侧边缘为自由边，在梯度升温的作用下，自由边无外部约束，因此在跨中截面边缘下挠最大。

综前所述，在恒载、活载和梯度升温作用下，板的变形均呈现出明显的空间变形特点，除支承处外，挠度沿板宽方向分布较为不均匀，在梯度温度作用下不均匀性更加显著，梁单元的平截面不能反映挠度沿板宽方向的分布，采用梁单元分析会偏离结构实际变形，低估活载和梯度升温作用下的挠度值。

3.2 内力计算

3.2.1 恒载作用下弯矩

由恒载作用下纵向弯矩图（如图4 所示）看出，恒载作用下边跨和中跨纵向最大正弯矩位于跨中，跨中纵向弯矩除板边缘区域外沿板宽方向分布基本均匀，边跨单位板宽最大纵向弯矩649.0Kn.m，中跨单位板宽最大纵向弯矩895.0Kn.m。纵向最大负弯矩位于中墩墩顶处，单位板宽最大纵向负弯矩-2904.2Kn.m。

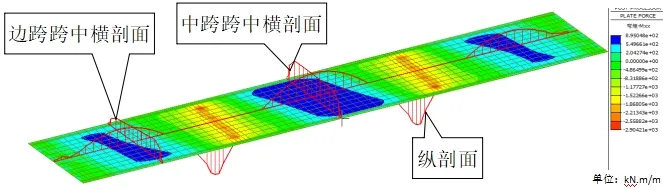
图4 恒载作用下纵向弯矩图

由恒载作用下横向弯矩图（如图5 所示）看出，横向负弯矩于墩顶处较大，中墩墩顶单位板宽最大负弯矩-441.2Kn.m，是最大纵向负弯矩的0.15 倍。横向最大正弯矩位于跨中，横向弯矩沿板宽方向近似成抛物线形分布，最大值位于板中线处。边跨单位板宽最大横向弯矩74.6Kn.m，是边跨跨中最大纵向正弯矩的0.11 倍；中跨单位板宽最大横向弯矩78.6Kn.m，是中跨跨中最大纵向正弯矩的0.08 倍。

图5 恒载作用下横向弯矩图

3.2.2 活载作用下内力

由活载作用下纵向弯矩分布图（如图6 所示）可看出，活载作用下边跨和中跨纵向最大正弯矩位于跨中，受活载偏载的影响，跨中纵向弯矩沿板宽方向分布比恒载作用下较为不均匀，边跨跨中单位板宽最大纵向弯矩262.1Kn.m，中跨跨中单位板宽最大纵向弯矩317.9Kn.m。纵向最大负弯矩位于中墩墩顶处，单位板宽最大纵向负弯矩-525.2Kn.m。

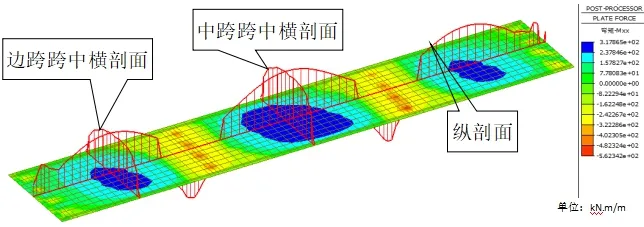
图6 活载作用下纵向弯矩分布图

由活载作用下横向弯矩分布图（如图7 所示）可看出，活载作用下横向正弯矩于墩顶处较大，中墩墩顶单位板宽最大横向正弯矩191.8Kn.m，为墩顶纵向负弯矩的0.38 倍。边跨及中跨跨中横向弯矩呈不规则的锯齿形分布，横向弯矩最大值位于板中线处，边跨跨中单位板宽最大横向弯矩102.6Kn.m，为同位置处纵向弯矩的0.39 倍，中跨跨中单位板宽最大横向弯矩107.8Kn.m，为同位置处纵向弯矩的0.34 倍。

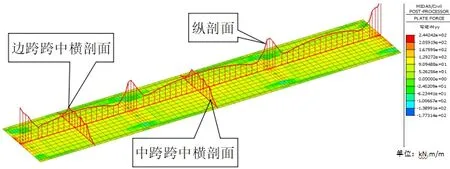
图7 活载作用下横向弯矩分布图

3.2.3 梯度升温作用下内力

由梯度升温作用下纵向弯矩分布图（如图8 所示）可看出，梯度升温作用下中墩附近区域及中跨纵向弯矩较大，最大正弯矩位于中墩墩顶处，墩顶单位板宽最大纵向弯矩为1217.5Kn.m。中跨纵向弯矩除板边缘区域外，纵向弯矩沿板宽方向分布基本均匀，中跨跨中单位板宽最大纵向弯矩645.3Kn.m。

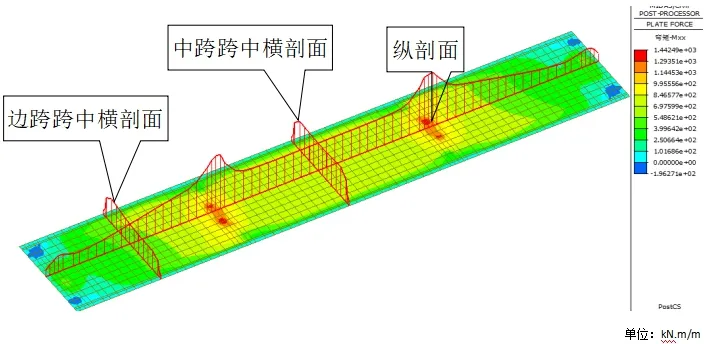
图8 梯度升温作用下纵向弯矩分布图

由梯度升温作用下横向弯矩分布图（如图9 所示）可看出，梯度升温作用下墩顶附近区域横向弯矩较大，最大横向正弯矩位于边墩墩顶附近，单位板宽最大横向正弯矩为334.4Kn.m，是同位置处纵向弯矩的0.97 倍，最大横向负弯矩位于中墩墩顶处，单位单位板宽最大横向正弯矩为-600.9Kn.m，是同位置处纵向弯矩的0.49倍。跨中横向弯矩呈抛物线分布，中间大，两边小，最大值位于板中线处，边跨跨中单位宽度最大横向弯矩155.2Kn.m，为同位置处纵向弯矩的0.30 倍。中跨跨中单位板宽最大横向弯矩87.1Kn.m，为同位置处纵向弯矩的0.13 倍。

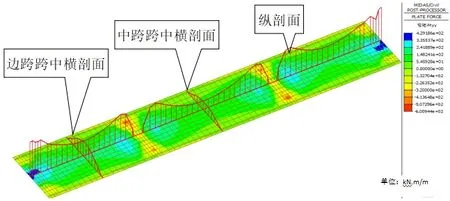
图9 梯度升温作用下横向弯矩分布图

综前所述，在恒载、活载和梯度温度荷载作用下，除桥墩附近区域外，纵向弯矩与梁单元模型弯矩图基本吻合，弯矩沿着板宽方向分布基本均匀。横向弯矩沿着板宽方向分布近似成抛物线形，最大值位于板中线处，在活载和梯度升温作用下，跨中横向弯矩达到纵向弯矩的0.3 倍以上，梯度升温作用下边墩墩顶处最大横向正弯矩达到纵向弯矩的0.97 倍，中墩墩顶处最大横向负弯矩达到纵向弯矩0.49 倍，因此对此类结构设计时不能忽视横向弯矩的影响，需重视横向受力分析，加强横向配筋设计。

4 结语

本文通过对桩板刚构桥的有限元分析，分别研究了桩板刚构桥在恒载、活载和梯度升温作用下的变形特点和内力分布趋势，建议对此类结构在设计中宜注意以下三点：

（1）对于宽跨比较大的板桥，梁单元模型分析会偏离结构实际变形，板单元模型可以准确反应结构变形和内力分布趋势，设计中宜采用板单元进行分析。

（2）宽跨比较大的板桥在荷载作用下，挠曲变形表现出明显的空间变形特点，不仅纵向产生变形，横向也会产生的不可忽略的变形，在梯度升温作用下横向变形更为显著。

（3）宽跨比较大的板桥在荷载作用下，结构中会产生较大的横向弯矩，要注意墩顶横向负弯矩和跨中横向正弯矩影响，设计中可以提取组合工况下的单位板宽的横向弯矩值，选取横向弯矩较大的控制截面进行配筋设计。