基于电气距离分区的配电网动态无功优化

武晓朦,孙丰玉,李 飞

(西安石油大学 电子工程学院,陕西省油气井测控技术重点实验室,陕西 西安 710065)

引 言

配电网动态无功优化是在静态优化的基础上探究配电网中负荷的动态变化以及无功补偿出力等不确定性因素,根据不同时刻调整优化方式,从而有效提升电压质量,减少网络损耗[1-3]。近年来,配电网中接入的分布式电源(distributed generation,DG)呈上升趋势,其可给配电网提供一定的功率支撑、丰富无功调控手段,但并网后易造成局部电压升高甚至电压越限,为此许多学者展开了相关研究工作。文献[4]提出一种基于混沌扰动和高斯变异改进的蜂群算法,完成多目标无功优化模型的求解;文献[5]针对配电网中负荷不确定性问题,通过预动作表法求得电容器的投切时刻与容量,利用权重系数法完成模型优化;文献[6]将多目标粒子群算法引用到无功优化,利用模糊隶属度函数从Pareto最优解集中获得一组折中解。以上文献均是对配电网整体进行全局无功优化,然而随着大量DG的接入,配电网拓扑结构越发复杂,相比于全局优化,配电网分区优化更利于满足无功优化精准性与快速性的要求。

目前主要有2种方式对配电网进行分区：网络结构分区法和自适应分区法[7]。网络结构分区法操作简单,不能适应如今结构日渐复杂的配电网发展趋势。自适应分区法中的聚类分析法和基于电气距离分区法应用最广,但前者无法确保分区后的子区域内有充足的无功支撑来实现瞬态无功补偿[8]。电气距离分区法主要受网络结构的影响,其变化趋势跟配电网拓扑结构相类似[9],对于分区后的子区域来说,此类方法在反映其结构性能的同时,还能反映节点之间电气耦合程度的强弱。

本文在现有理论基础上,建立一种将配电网集中控制与分区控制结合起来的无功优化模型,考虑日负荷及DG出力水平的变化对配电网进行动态无功优化。当配电网中出现节点电压越限,执行基于电气距离的分区控制,对越限节点所在子区域进行局部优化;电压不越限则执行集中控制,进行基于Pareto最优解集的多目标无功优化。

1 DG无功调节特性及动态无功优化模型

1.1 DG无功调节分析

部分DG通过逆变器并网,能够实现连续无功调节,弥补并联电容器组等离散变量不能进行快速无功补偿的缺点。DG的无功电压调节与DG本身的结构以及并网方式有关。本文考虑风光接入的配电网,选择风力发电中的双馈感应风电机组(doubly-fed induction generator,DFIG)以及分布式光伏(photovoltaic,PV)的无功出力可调范围作出分析。

(1)DFIG并网

DFIG的定子侧通过变压器并网,其无功调节范围受定子侧及转子侧电流影响,如下式所示：

(1)

(2)

式中：Pm为风电机组输入机械功率;s为电机的转差率,s=(ω1-ωr)/ω1,ω1、ωr分别表示同步旋转、转子旋转角速度;Qs为定子侧注入的无功功率;Us为定子电压的有效值;Is,max、Ir,max分别表示定子、转子电流有效值的极大值;Ls、Lm分别表示定子、励磁电感。

转子侧通过转子侧变压器与网侧变流器并网,其无功调节范围如下：

(3)

式中：Qc为网侧变流器输入的无功功率;Sc,max为网侧变流器容量极大值。

综合考虑定子侧和网侧无功调节,DFIG的无功调节范围如下：

(4)

式中：Qmax、Qmin分别表示DFIG无功调节的极大值、极小值;Qs,max、Qs,min分别表示定子侧无功调节的极大值、极小值;Qc,max、Qc,min分别表示网侧变流器无功调节的极大值、极小值。

(2)PV并网

PV通过逆变器并网。逆变器由于具有无功控制的功能,因此能够为配电网提供电压支撑。如下式所示,其容量可以决定PV可调的无功范围。

(5)

式中：QPV,max、QPV,min分别表示光伏逆变器的最大、最小无功输出;PPV为PV有功出力;Sinv表示光伏逆变器容量。

1.2 数学模型

本文数学模型中的目标函数包括：一天内的网损最小、电压偏差最小、电压平均偏离最小。针对多个目标优化问题,选用Pareto最优解集法进行求解。约束条件分为等式约束和不等式约束。不等式约束为各时刻变压器变比、DG无功出力约束、配电网节点电压约束。所建数学模型如下所示。

(1)目标函数

(6)

(7)

(8)

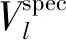
(2)约束条件

(9)

Timin,t≤Ti,t≤Timax,t,

(10)

QDGmin,t≤QDG,t≤QDGmax,t,

(11)

Vimin,t≤Vi,t≤Vimax,t。

(12)

其中：式(9)为等式约束,Pi,t、Qi,t分别表示t时段内节点i的有功、无功功率;Bij,t为节点电纳。式(10)～(12)为不等式约束,Ti,t、Timax,t和Timin,t分别表示t时段第i个可调变压器的变比及其变比可调范围上下限;QDG,t、QDGmax,t和QDGmin,t分别表示t时段DG的无功出力及其出力可调范围上下限。

2 配电网分区

2.1 基于灵敏度的电气距离分区法

电气距离矩阵用来表示配电网内各节点的耦合关系,其值越小,节点间联系越强。首先需要利用潮流计算得到雅可比矩阵,然后对其求逆,得出灵敏度矩阵,进而求得节点间的电气距离矩阵：

Dij=Dji=-lg(αij·αji)。

(13)

式中：αij表示为节点i,j电压变化量之比,其表达式为：

(14)

本文使用的是牛顿法潮流计算,其功率修正方程的矩阵形式表示为：

(15)

式中：J为雅可比矩阵,用来说明功率与节点电压之间的偏导关系;ΔP、ΔQ分别表示节点注入有功功率、无功功率的偏差矩阵;Δθ、ΔV分别表示节点电压相角、电压幅值的变化矩阵。对式(15)求逆可得：

(16)

式中：S为灵敏度矩阵;SPU、SQU分别表示有功电压、无功电压灵敏度因子,用来说明系统节点的功率变化导致节点电压发生变化;SPθ、SQθ则用来说明系统节点的功率变化导致电压相角发生变化。S值的大小可以反映节点拓扑结构联系的紧密度。

忽略相角和有功功率对电压的影响,由式(16)可以得到无功电压灵敏度矩阵：

ΔV=[SQU]·ΔQ。

(17)

结合式(14)和(17)可得出电气距离矩阵。

配电网不同时间段负荷变化量和DG注入功率不同,因此节点电压变化量随时间变化而变化。根据不同时间节点电压的变化求得电气距离,可以动态调整配电网的分区情况,调整分区里的电压无功控制范围。

2.2 分区方法实现步骤

(1)对配电网进行潮流计算,得功率修正方程;

(2)利用功率修正方程计算配电网中每个DG单独作用时的节点电压灵敏度矩阵;

(3)区域直径表示为分区内电气距离最大的2个节点之间的电气距离[10]。以DG作为子分区的第一个节点,并以灵敏度系数、节点联通情况、区域直径为约束条件执行配电网分区。

3 差分进化算法的改进

传统差分进化算法(differential evolution,DE)的主要操作有初始化、变异、交叉、选择。针对该算法后期容易出现早熟收敛或搜索停滞等缺点,本文在传统算法的基础上做了改进。

3.1 初始化种群的改进

(1)混沌初始化策略

混沌搜索策略能提高算法的搜索能力,广泛应用于优化搜索问题。本文采用线性幂函数混合映射,研究表明,线性幂函数混合映射的随机性与遍历性比一般Logistic映射性能更优,其数学表达式为[11]：

(18)

式中：rk为第k次初始化后的值;μ为控制参数,值取4;00.1。

在DE算法的初始化中引入线性幂函数混合映射,有利于保持算子的多样性,找寻目标函数最优解。

(2)反向学习初始化策略

初始化中引入反向学习能得到遍及解空间的初始化算子。经过上文提到的混沌初始化后形成种群X,种群X经反向学习后生成一组反向解OX,OX与X共同组成一组新初始化种群,对其进行快速非支配排序,择优进入算法循环。其定义如下：

若X是定义在实数集R上一区间[a,b]中的实数,X∈[a,b],X的反向解OX为：

OX=a+b-X。

(19)

3.2 自适应参数的改进

DE算法中的自适应参数有缩放因子F与交叉概率CR。在传统DE算法中,2个参数的取值往往根据决策者的经验自行设置,以致算法后期收敛性较差。本文在进行了自适应参数改进后,能够根据进化代数的不断增大,动态调整F和CR的取值。在进化前期,F和CR取值较大,算法搜索能力强;在进化末期,F和CR取值逐渐减小,算法寻优能力强,避免种群出现局部最优的状况。

(20)

式中：Fmax、Fmin分别表示缩放因子的极大值、极小值,设置数值为2、0;CRmax、CRmin分别表示交叉概率的极大值、极小值,设置数值为1、0;gen为当前进化代数;G为总进化代数。

4 无功优化模型求解流程

根据上述理论依据与设计过程,本文所提优化方式实现流程图如图1所示。求解步骤为：

(1)读入数据,以潮流计算的结果为输入,计算配电网的节点电压;

(2)判断节点电压是否越限;

(3)若节点电压越限,根据2.1节的方法对配电网进行分区处理,并利用第3节提出的改进DE算法进行局部优化,输出Pareto最优解;

(4)若节点电压不越限,利用第3节提出的改进DE算法进行全局优化,输出Pareto最优解。

图1 无功优化模型求解流程Fig.1 Solution process of reactive power optimization model

5 算例及结果分析

5.1 算例

算例采用IEEE-33节点系统,其拓扑结构如图2所示。系统基准电压12.66 kV,基准容量10 MVA,节点电压额定值1.05 p.u.。节点24、30处加入DFIG,装机容量0.8 MW;节点9、19处加入PV,装机容量0.6 MW。10～380 kV配电网节点电压偏差允许范围为额定电压的7%,所以本文设定节点电压上限为1.07 p.u.,下限为0.93 p.u.。改进DE算法的种群数为100,迭代次数为200。

图2 IEEE-33节点系统网络拓扑图Fig.2 Network topology of IEEE-33 node system

5.2 结果分析

选取某地一天的负荷数据,采用文献[12]中DFIG及PV出力数据为计算依据,结合IEEE-33系统原负荷规模,模拟系统等效日负荷曲线。为了避免无功调节设备的频繁动作,采用文献[13]中的信息熵分段法,对由日负荷曲线、风力发电与光伏发电的日出力曲线组成的等效日负荷曲线进行分段处理。每一时段内,等效日负荷值相同,优化后的DG无功出力相同,每一时段只需调节一次DG的无功出力。基于信息熵分段法得出的最佳分段为7段。图3为最优分段结果图,分段结果与负荷曲线走势相符。不同时间段内的节点电压曲线如图4所示。

图3 等效日负荷曲线分段结果Fig.3 Segmented results of equivalent daily load curve

图4 各时段的节点电压Fig.4 Node voltage in each period

由图4可以看出,在时段1有部分节点电压越下限,其余时段电压在合格范围内。本文选取时段1和时段2为例进行优化。

时段1中,出现节点电压越下限情况,首先对配电网进行分区处理,分区结果如图5虚线框所示,各区域节点形成顺序见表1。

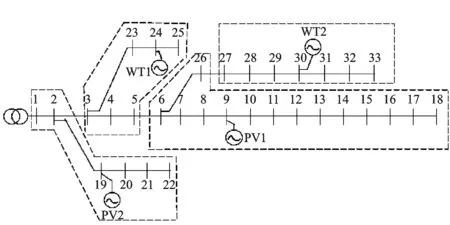
图5 IEEE-33系统分区结果Fig.5 Partition results of IEEE-33 system

表1 各区域节点形成顺序Tab.1 Formation order of regional nodes

对电压越限节点所在分区进行局部无功优化,并与全局优化进行对比。图6对比了节点电压优化情况,重复进行3次实验得到表2,表中列出了不同优化方式下的DG无功出力、系统网损及优化时间。

图6 节点电压优化结果Fig.6 Optimization results of node voltage

由图6可以看出,对配电网电压越限节点所在分区进行局部优化与对配电网整体进行全局优化都可以提高节点电压水平,但在节点6到节点18局部优化优于全局优化。

对2种优化方案分别进行3次实验,实验结果见表2。分区优化的平均网损为0.143 MW,平均优化时间为30.27 s,仅对电压越限区的PV1和WT1进行调节即可满足要求;全局优化的平均网损为0.141 MW,平均优化时间为37.52 s,需对全部DG进行调节,网损比分区优化少2 kW,但优化时间慢于分区优化7.25 s。

表2 不同优化方式下的无功优化结果Tab.2 Reactive power optimization results using different optimization schemes

时段3中,节点电压未出现越限,利用改进的DE算法进行配电网全局多目标无功优化,采用文献[14]中提出的改进理想点决策方法对输出的Pareto最优解集进行折中处理,处理后得到的是一组折中解,所得Pareto最优前沿及折中解如图7所示。

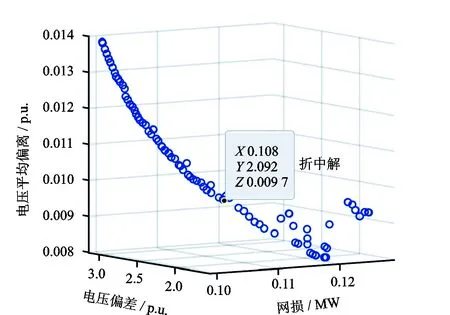
图7 Pareto最优前沿及折中解Fig.7 Pareto optimal frontier and compromise solution

经过全局优化后配电网的网损为0.108 MW,电压偏差为2.092 p.u.,电压平均偏离为0.009 7 p.u.。在同一时刻,接入DG但未进行无功优化时,配电网的网损为0.165 MW,电压偏差为5.308 6 p.u.,电压平均偏离为0.012 3 p.u.。优化后的目标函数均优于优化前。

6 结 论

本文为解决DG接入配电网造成的电压不稳定、越限等问题,将配电网全局优化与分区优化结合起来,通过改进DE算法进行优化求解。在电压越限的情况下,分区优化优于全局优化,具体体现在：所用时间少,不需要对全部DG进行调节;在电压未越限的情况下,进行配电网全局优化,采用改进DE算法得到的目标函数明显优于优化前。