一种改进非奇异终端的滑模控制策略*
2023-06-05刘陵顺孙美美李永恒
刘陵顺 孙美美 李永恒
(1.海军航空大学航空基础学院 烟台 264001)(2.92781部队 三亚 572029)
1 引言
滑模变结构控制器对系统内部参数变化和外部扰动不敏感,具有较好的动态性能和极强的鲁棒性[1~5]。对于滑模变结构控制算法来说,选择合适的滑模面是设计控制器至关重要的一步[6~7]。合适的滑模面能够改善系统动态品质和稳态精度。线性滑模面是滑模控制系统最早出现的,也是应用最广的。但线性滑模面存在一大缺陷,系统状态从到达滑模面至运行到平衡点的过程是以指数形式收敛的,系统状态只能无限趋近于平衡点,无法真正到达平衡点。文献[8]以PMSM 电机转速为状态变量,设计了一种积分滑模控制器,采用饱和函数替代符号函数,进一步降低系统抖振。同时,利用积分滑模面设计负载转矩观测器,消除负载转矩变化对电机转速的影响。但是负载转矩观测器设计的前提在于,假定负载转矩求导为零。而实际电机调速系统逆变器开关频率较高,采样周期非常小,单位时间内负载转矩变化量不为零。文献[9]设计一种分数阶滑模面,用于分数阶混沌系统之间的同步,并给出误差方程的稳定性判据。通过分数阶Chen 系统与新混沌系统之间数值仿真,证明所设计分数阶控制器的有效性。
相比线性滑模控制方法,终端滑模控制方法能够保证系统状态在有限时间到达滑模面,继而在有限时间收敛到平衡点,适用于非线性滑模系统。文献[10]针对终端滑模控制系统控制量无限大问题,提出一种非奇异终端滑模面。该滑模面与终端滑模面结构差异不大,能够解决终端滑模面的奇异性问题。但当系统状态到达滑模面,远离平衡点时,收敛速度小于相同参数的线性滑模面。针对这一不足,文献[11]提出一种非奇异快速终端滑模面。相比非奇异终端滑模面,拥有较快的收敛速度。文献[12]结合非奇异快速终端滑模面的优点,提出一种混合非奇异终端滑模面。混合非奇异终端滑模面可根据系统状态大小,选择不同滑模面参数。实验结果表明,控制器在保持收敛速度的同时,降低了系统抖振。
2 问题提出
考虑二阶非线性单输入单输出(SISO)系统如下所示:
对于式(1)所示的二阶SISO 系统,滑模控制算法一般选用传统线性滑模面:
式中,e1=x1-xd为跟踪误差,xd为控制目标,e2=,参数c>0。当系统状态轨迹到达滑模面,此时
从上式可知,系统状态从到达滑模面至运行到平衡点的过程是以指数形式收敛的,这意味着系统状态只能无限趋近于平衡点,无法真正到达平衡点。
终端滑模控制算法能够保证系统状态在有限时间到达滑模面,继而在有限时间收敛到平衡点,但终端滑模控制存在奇异性问题。为克服终端滑模奇异性问题,Feng Y 等[3]提出一种非奇异终端滑模控制算法(NTSM)。其滑模面s,控制作用u 数学表达式为
式中,参数β、η>0 ,p、q为奇数且满足1 <q<p<2q。当系统状态轨迹到达滑模面,此时
从上式可知,指数项q/p<1,当系统状态到达滑模面,距离平衡点较远时,收敛速度小于相同参数的线性滑模面。
为克服以上缺点,Yang L 等[4]提出一种非奇异快速终端滑模控制方法(NFTSM)。其滑模面s,控制作用u数学表达式为
式中,g、h、p、q为正奇数且满足g/h>p/q,参数α>0。当系统状态到达滑模面,距离平衡点较远时,e1的高次项起主要作用,此时
收敛速度大于NTSM。当系统状态到达滑模面,距离平衡点较近时,忽略e1的高次项,此时收敛速度近似于NTSM。
虽然NFTSM 克服了NTSM 系统状态远离平衡点时,收敛速度不足的缺点,但NFTSM 缺点明显。对式(7)求导,并将式(1)、(8)代入,求得趋近速度为
根据上式,在参数相同情况下,NFTSM 从初始状态到达滑模面的趋近速度与NTSM 趋近速度相同。由于滑模面s 存在e1的高次项,NFTSM 初始状态s(0)大于NTSM初始状态,导致NFTSM到达滑模面时间大于NTSM。尤其对于跟踪误差较大的系统,e1的高次项会极大地增加初始状态s(0)与滑模面之间的距离。
3 改进非奇异终端滑模面
对于NTSM 来说,选择较大的非线性增益η,可以加快趋近速度,但会影响系统稳态收敛精度,造成较大抖振,甚至激发系统未建模部分,引发高频振荡。同样,选择较小的滑模面参数β可以加快趋近速度,但有两个缺点:一是会影响系统稳态精度,二是系统状态到达滑模面,距离平衡点较远时,收敛速度较为缓慢。
为提高滑模控制系统的收敛速度,本节提出一种改进NTSM,其滑模面定义为
式中,e1=x1-xd为跟踪误差,xd为控制目标,e2=,参数β、r>0 且0 <α<1,p、q为奇数且满足1 <q<p<2q,x1(0)为系统初始状态。
定理1对于系统(1),选择如式(11)所示的改进NTSM,选择控制律
则系统可在有限时间内到达滑模面。
证明 选择Lyapunov函数
对上式求导,可得
将式(12)代入,得
因为|g(x) |<lg,推导出≤0,系统满足Lyapunov稳定性条件,可在有限时间内到达滑模面。
通过与NTSM 比较,本节设计的改进NTSM 相当于根据系统状态x1自适应调节参数β。根据式(16),随着状态x1向平衡点靠近,通过调节参数α,使系统维持较快的趋近速度,减小到达时间。当系统状态到达滑模面时,收敛到平衡点的速度近似于NTSM,且收敛到平衡点的曲线更为光滑。此外,改进NTSM 参数α有两个作用:一是防止终端滑模控制出现奇异性问题;二是α的大小决定系统初始状态的收敛速度。参数r有一个作用:r的大小决定系统具有较快趋近速度的滑模面范围。
定理2对于系统(1),选择如式(11)所示的改进NTSM,则系统从到达滑模面的状态x1(tr)至收敛到平衡点xd=0的时间是有限的。
证明当系统状态到达滑模面时,此时
整理,可得
对两端求积分,得
因为系统状态平衡点xd=0,可得
由此定理得证。
根据系统(1),系统不确定量及外部扰动g(x)是有界的,即但在实际生产生活中,g(x)是不断变化的,很难测量上确界lg,且上确界lg测量的不精准,会影响系统稳态收敛精度,造成较大抖振,甚至激发系统未建模部分,引发高频振荡。
为了克服不确定量及外部扰动g(x)对控制系统的影响,本节以系统状态和外部扰动g(x)为对象,设计一种带有扰动的滑模观测器。
定理3对于系统(1),选择如式(11)所示的改进NTSM,设计扰动观测器
式中,l1、l2>0,为系统状态x2、外部扰动g(x)的估计值,为系统状态观测误差。选择控制律
证明定义Lyapunov函数为
假设g(x)为慢时变信号,化简式(24),并将式(1)、式(21)代入,可得
将式(22)代入,得
定义δ(t)=>0,则
定理得证。
采用带有外部扰动的滑模观测器,克服了外部扰动g(x)难以测量的缺点,增强系统抗干扰能力,减小了抖振。
4 控制性能分析
以二阶系统为例,用以说明改进NTSM 相比于NTSM的优点。二阶系统状态方程为
参数p=5,q=3,α=0.1,r=0.05,β=10,η=20,初始状态x1(0)=500。滑模面s和系统状态x1如图1、2所示。
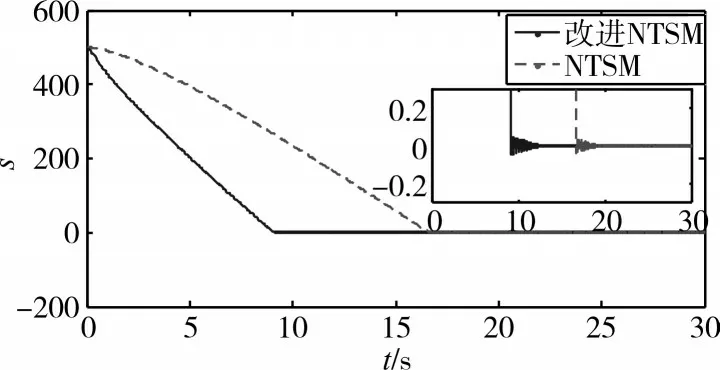
图1 滑模面s
从图1、图2 可以看出,改进NTSM 拥有更快的趋近速度,到达滑模面时的抖振近似于NTSM。改进NTSM 从到达滑模面至平衡点时间为3.54s,NTSM 为2.75s,前者收敛到平衡点的曲线更为光滑,符合前文理论推导。

图2 系统状态x1
5 结语
本文针对传统非奇异终端滑模控制方法收敛速度慢等缺点,提出一种基于改进非奇异终端滑模的无位置传感器控制方法。首先阐述了非奇异快速终端滑模面的缺点,分析了改进非奇异终端滑模面参数的意义,理论证明系统状态从到达滑模面至收敛到平衡点的作用时间是有限的。最后通过仿真验证,对比了非奇异终端滑模控制方法和改进非奇异终端滑模控制方法,针对同一系统,后者能够有效提高观测系统收敛速度,减小抖振。
