双级孔含油轴承油压扩散与表面渗析特性分析

2023-06-05张国涛蔡伟杰尹延国韦习成

摩擦学学报 2023年5期

张国涛, 蔡伟杰, 尹延国, 韦习成

(1.安徽工业大学机械工程学院, 安徽马鞍山 243000;2.合肥工业大学摩擦学研究所, 安徽合肥 230009;3.上海大学材料科学与工程学院, 上海 200444;4.上海大学(浙江) 高端装备基础件材料研究院, 浙江嘉兴 314100)

含油轴承采用粉末冶金工艺制备，具有自润滑、轻量化和近净成形特性，在当前机械产品追求高性能、低能耗和环境友好性的现状下具备显著技术优势.如在新能源汽车的发动机气门阀座、气门导管以及变速箱中的齿轮、轴承和止推环等关键摩擦副中，含油轴承材料均有广泛应用[1-2].作为典型机械传动基础件，含油轴承的润滑性能与服役质量对整机运行状态具有重要影响[3-4].

含油轴承工作时，轴承基体孔隙中储存的润滑油在轴承间隙与多孔基体间循环流动，在摩擦界面形成具有一定承载能力的动压油膜.关于含油轴承油膜润滑性能的研究历来受到国内外学者的重视[5-7].研究表明，当载荷和转速合理匹配时，轴承摩擦界面的动压油膜足以抵挡外负载，含油轴承处于流体润滑状态[8-10].在流体润滑状态前提下，研究人员围绕含油轴承的润滑模型与数值分析开展了大量研究.大多工作聚焦于探讨含油轴承表面的润滑性能，数值分析不同孔隙结构、轴承渗透率及油液非牛顿特性等对油膜润滑性能的影响[11-14].这些研究表明，含油轴承基体孔隙中的渗流场变化对油膜的流体动压力与润滑特性有显著影响.与单层多孔质含油轴承相比，具有双级孔隙分布的含油轴承通过调控不同层间孔隙搭配，在轴承的承载能力和工作性能方面具有明显优势[15-16].研究人员通过考察双级孔含油轴承的润滑特性，分析轴承基体孔隙结构对油膜压力分布规律的影响.本文作者所在课题组也采用粉末冶金方法，制备了双级孔含油轴承材料，结合数值模拟和摩擦学试验结果初步探讨了双级孔含油轴承的渗流行为和自润滑机理[17].上述研究丰富了含油轴承的渗流润滑理论，为含油轴承润滑特性分析与轴承结构的润滑设计提供了理论指导.综上分析可见，含油轴承基体中油液的渗流行为已经引起研究人员广泛关注，相关研究聚焦于孔隙渗流对轴承摩擦界面油膜润滑性能的影响，对轴承表面油液的析出现象以及轴承基体中的油压扩散特性还较少报道，涉及双级孔含油轴承基体渗流行为与压力扩散相互作用方面的研究更少见，而这恰对揭示含油轴承油膜润滑机理以及指导多孔结构的合理设计极为重要.本文中以具有两层孔隙分布的双级孔含油轴承为研究对象，分析多孔基体中渗流流场与油液压力的分布规律，研究双级孔隙结构中流体渗流与压力扩散的相互作用，研究工作为明晰双级孔含油轴承润滑机理提供一定理论依据.

1 双级孔含油轴承润滑模型

双级孔含油轴承摩擦副的示意图如图1所示，在摩擦副系统中建立坐标系：在轴承间隙区采用极坐标系(θ,r,z)表述，在多孔轴承材料内部采用极坐标系表述.O和分别为上下试样中心，上试样材料接触面为实体淬火钢环，内径和外径分别用ri和ro表示，下试样为双级孔含油轴承，轴承基体中双层材料的渗透率分别为k1和k2，厚度分别为△1和△2，上试样旋转角速度为ω，接触面间中心膜厚为h0，并假设上试样和下试样表面光滑.

Fig.1 Schematic diagram of ring-face contact oil bearing system图1 环面接触摩擦副运动形式

在环面接触摩擦副常见的止推轴承或机械密封中，由于支撑结构或变形作用下，接触面间常存在一定倾角β，假设接触面上任意一点M(θ,r, 0)处的膜厚为h，则任一点膜厚方程

假设摩擦副处于稳态运行工况，认为密度和黏度为常数，忽略热效应影响.分别用纳维斯托克斯方程和达西定律来描述油膜区和多孔基体中的流体流动.得到极坐标下油膜区流体控制方程[10]：

式中，p为油膜区中的流体压力，为多孔基体中的流体压力.µ为油膜区中的流体黏度，为多孔基体中的流体黏度.

在含油轴承材料中，假设轴承具有各向同性，由极坐标系下达西定律可知表层多孔轴承中油液在3个方向上的渗流速度为

式中，ki表示两层多孔质中的渗透率，下角标i=1和2分别代表表层和基层两层多孔介质.

稳态情况下，描述多孔质中流体的流量连续性方程为

将方程(3)~(5)代入方程(6)中，得到双级孔隙中流体流动的统一控制方程为

油膜区变形Reynolds方程无量纲化形式

两层多孔质中的统一控制方程无量纲形式

无量纲油膜承载力G可表示为

无量纲流体摩擦力公式

对上述模型进行边界条件设置：含油轴承摩擦表面上的内环面压力和外环面压力均设置为为环境压力，在油膜破裂位置采用Reynolds边界条件捕捉油膜边界，周向上油膜压力采用压力循环边界条件，对轴承底面采用不可渗透边界.分析润滑性能时，需要对上述偏微分方程组进行求解.图2所示为含油轴承渗流润滑模型的计算程序框图.首先，为轴承结构和润滑油参数指定初始值，油液的初始压力和初始速度均设置为零，并对双级孔隙中的流体控制方程(8)和方程(9)进行数值计算，得到渗流场和压力场.利用油膜区域与含油轴承之间的压力连续性边界条件，计算轴承表面上的法向渗流压力.将法向渗流压力耦合到油膜区控制方程中，反复迭代计算轴承系统渗流场和压力场，计算迭代后的结果与前一步计算结果的相对误差值，将油压相对误差小于10−4作为油压收敛判据，满足收敛判据后退出压力迭代循环，采用复化Simpson积分公式计算油膜的承载力和摩擦力，根据方程(10)和方程(11)求出油膜的无量纲承载力和摩擦力，两者相除即可得油膜的摩擦系数.数值分析过程中，参考文献[10, 17-18]，选取以下计算参数：ri=22 mm，ro=30 mm,μ=0.02 Pa·s，h0=4×10−6m，△1=△2=2 mm，ω=2000 r/min，β=0.5×10−4~2.5×10−4rad，k1=1×10−16~1×10−12m2，k2=1×10−13m2.

Fig.2 Calculation program diagram of seepage lubrication model of oil bearing图2 含油轴承渗流润滑模型的计算程序框图

2 结果与讨论

为便于分析轴承厚度方向上的油压扩散特性，在含油轴承内部选择3个层面来展示油液压力的分布形态：处于含油轴承最表层的摩擦界面、两层材料间的层间界面和轴承底面.摩擦副间的油膜压力与多孔介质内部的流体压力扩散结果如图3所示.计算图3所示结果时表层渗透率k1的取值为1.25×10−14m2.由如图1所示的倾斜环面副可知，摩擦副相对旋转过程中，转角在(0, π)范围内时，摩擦副间的楔形空间是发散的，对应转角位置为从最小油膜厚度逆时针旋转到最大油膜厚度；在(π, 2π)范围内时，摩擦副间的楔形空间是收敛的，对应转角位置为从最大油膜厚度逆时针旋转到最小油膜厚度.因此图3中流体动压力主要在收敛区(π, 2π)转角范围内产生.在摩擦界面上，流体动压力主要发生在环面接触区中的收敛区，轴承圆心处流体压力为零；从摩擦界面到轴承底面，流体压力逐渐由环面接触区向圆心部位扩散传导，流体动压力作用面积逐渐增大，压力峰值逐渐降低.

Fig.3 Oil film thickness and pressure distribution in toroidal friction pair system: (a) oil film thickness; (b) pressure distribution on friction face; (c) pressure distribution on interlayer face; (d) pressure distribution on bottom face图3 环面摩擦副系统中的油膜厚度与压力分布：(a)油膜厚度；(b)摩擦面上压力分布；(c)层间界面上压力分布；(d)轴承底面上压力分布

2.1 油压扩散特性分析

参考文献中的参数取值[10,17-18]，倾角变化范围为0.5×10−4~2.5×10−4rad，渗透率k1=1×10−14m2，k2=1×10−13m2，其他参数保持不变，计算分析倾角变化对摩擦副间的油膜压力和多孔介质内部的流体压力扩散的影响，结果如图4所示.对比图4(a)、(b)和(c)可见，油膜压力在周向呈反向正弦分布，在收敛区间时，随着倾角增大，所选取3个界面上的周向流体压力均增大，在发散区间时，随着倾角增大，所选取3个界面上的周向流体压力均减小.观察图4(a)和(a')可见，环面摩擦副间倾角越大，摩擦副间的最小油膜厚度越小(这可以由环面接触摩擦副结构及油膜厚度公式可推得)，在摩擦界面上所形成的油膜动压力的峰值越高.在图4(b~c')所示的多孔轴承基体内部流体压力中，随着倾角增大，多孔轴承层间界面和轴承底面上的压力峰值增大，说明摩擦界面间的动压油膜压力向多孔基体中的扩散效应增强.对比图4(a')、(b')和(c')也可发现，由于图4(a')中轴承表面非摩擦区域的油液压力为环境压力，因此摩擦面上的油膜动压力将逐渐向多孔轴承内部和圆心处扩散传导，故在图4(b')和(c')所示的含油轴承内部，非摩擦区域对应位置上的流体压力范围逐渐增加，流体压力逐渐向圆心处扩散.但越靠近圆心部位，流体压力扩散的能力越弱，倾角变化对径向上压力分布的影响也越小，如在图4(b')和(c')的层间界面和轴承底面上，不同倾角影响的4条径向压力曲线几乎重叠到一起.

Fig.4 Dimensionless pressure distribution on three layers under obliquity: (a) distribution of dimensionless pressure along the circumferential direction on the friction interface; (a') radial distribution of dimensionless pressure on friction interface;(b) distribution of dimensionless pressure along the circumferential direction at the interlayer interface; (b') radial distribution of dimensionless pressure at interlayer interface; (c) distribution of dimensionless pressure along the circumferential direction on the bottom surface of bearing; (c') radial distribution of dimensionless pressure on the bottom surface of bearing图4 倾角作用下三个层面上的无量纲压力分布：(a)摩擦界面上无量纲压力沿周向的分布；(a')摩擦界面上无量纲压力沿径向的分布；(b)层间界面上无量纲压力沿周向的分布；(b')层间界面上无量纲压力沿径向的分布；(c)轴承底面上无量纲压力沿周向的分布；(c')轴承底面上无量纲压力沿径向的分布

图5所示为两种渗透率下环面摩擦副系统的油膜承载能力和摩擦系数随倾角的变化.图5(a)所示为选取渗透率k1=1×10−14m2，k2=1×10−13m2时的计算结果，可见随着倾角增大，摩擦面间动压油膜的承载能力增大，油膜的摩擦系数增大.承载能力增加是由图4中油膜压力峰值随倾角变化所决定的，而摩擦系数的变化显著不同于实体轴承的润滑分析结果(常见轴承润滑特性分析中，油膜压力越大，承载能力越高，摩擦系数越小).图5(b)所示为选取渗透率k1=1×10−16m2，k2=1×10−13m2时的计算结果，可见随着倾角增大，摩擦面间动压油膜的承载能力增大，油膜的摩擦系数降低，这符合实体轴承润滑理论的分析结果.当表层孔隙率较小时，多孔含油轴承与常见实体轴承的润滑特性类似，即油膜的摩擦系数和承载能力随倾角变化而变化的趋势一致.

Fig.5 Oil film carrying capacity and friction coefficient of ring friction pair system vary with inclination at two permeabilities:(a) k1=1×10−14 m2, k2=1×10−13 m2; (b) k1=1×10−16 m2, k2=1×10−13 m2图5 两种渗透率下环面摩擦副系统的油膜承载能力和摩擦系数随倾角变化：(a) k1=1×10−14 m2, k2=1×10−13 m2；(b) k1=1×10−16 m2, k2=1×10−13 m2

实际上，当含油轴承的渗透率无限小时，含油轴承的孔隙率接近为零，此时含油轴承就是实体(不可渗透)轴承.如前所述，增大摩擦副倾角能使最小油膜厚度减小，接触面间的油膜动压效应增强，油膜的摩擦系数降低，油膜承载能力提高，同时也易于向多孔基体中渗流和扩散.当表层孔隙率较大时，较高的孔隙率进一步增强了油液向多孔介质中的渗流及压力扩散效应，反过来也会削弱增大倾角后油膜压力的增大幅度[如图5(a)中油膜承载能力的增加幅度不如图5(b)中油膜承载能力大]，同时渗流和扩散效应的增强也会削弱摩擦系数的降低趋势.显然，摩擦系数随孔隙率的变化比承载能力更为敏感，当取表层渗透率k1=1×10−14m2时，摩擦系数已然随着倾角增加而增加.由此可猜想，表层渗透率在1×10−16~ 1×10−14m2之间必然存在某一个值，使得摩擦系数随倾角变化而产生的变化趋势发生反转.

为反映表层渗透率对摩擦副间的油膜压力与多孔介质内部的流体压力扩散的影响，图6所示为表层渗透率作用下摩擦界面、层间界面和轴承底面上的无量纲油膜压力分布曲线，计算时选取倾角为2×10−4rad.由图6(a)、(b)和(c)可见，所选取的3个界面上的周向流体压力分布与图4中分析的结果类似，即在收敛区间时，随着表层渗透率减小，所选取3个界面上的流体压力均增大，在发散区间时，随着表层渗透率减小，所选取3个界面上的流体压力均减小.不同的地方在于，当渗透率低于1×10−14m2时，渗透率变化对各界面上发散区间内某一区域的流体压力的影响较小，如图6(a)、(b)和(c)中的发散区间内，流体压力基本上不随渗透率变化而变化.这是由于发散区间内是油膜破裂与溃灭的过程，油膜动压力的峰值较小，向多孔轴承基体中的扩散效应较弱，而较小的轴承渗透率又进一步削弱了这种扩散效应，因此当轴承渗透率低至一定程度时，流体压力向多孔基体中的渗流与扩散几乎可以忽略；并且越靠近轴承底面，流体压力值越小，扩散效应越弱，更大区域内的流体压力不受渗透率影响.在图6(a')、(b')和(c')中，随着表层渗透率减小，所选取3个界面上的径向流体压力均增大，其流体压力扩散及分布趋势和图4中径向压力的分析过程类似.

Fig.6 Dimensionless pressure distribution at three levels under surface permeability: (a) distribution of dimensionless pressure along the circumferential direction on the friction interface; (a') radial distribution of dimensionless pressure on friction interface;(b) distribution of dimensionless pressure along the circumferential direction at the interlayer interface; (b') radial distribution of dimensionless pressure at interlayer interface; (c) distribution of dimensionless pressure along the circumferential direction on the bottom surface of bearing; (c') radial distribution of dimensionless pressure on the bottom surface of bearing图6 表层渗透率作用下三个层面上的无量纲压力分布：(a)摩擦界面上无量纲压力沿周向的分布；(a')摩擦界面上无量纲压力沿径向的分布；(b)层间界面上无量纲压力沿周向的分布；(b')层间界面上无量纲压力沿径向的分布；(c)轴承底面上无量纲压力沿周向的分布；(c')轴承底面上无量纲压力沿径向的分布

图7所示为轴承层间界面及轴承底面上圆心处压力随表层渗透率变化，由图7可见，轴承层间界面及轴承底面上圆心处的压力均随表层渗透率增大而增大.并且，当表层渗透率从1×10−16m2增大到1×10−15m2的过程中，两处的压力呈现出小幅度增加趋势；当表层渗透率从1×10−15m2增大到1×10−13m2的过程中，两处的压力显著增加.渗透率越大，油压在多孔基体中的扩散效果越强.

Fig.7 Variation of pressure at the center of the circle on the interlayer interface and bearing bottom face with permeability 图7 层间界面及轴承底面上圆心部压力随渗透率的变化

图8所示为表层渗透率对环面副的油膜承载能力及摩擦系数的影响.由图8(a)可见，表层渗透率k1的取值范围为1×10−16~ 1×10−12m2，随表层渗透率增加，油膜承载力先迅速降低后趋于平缓，结合整体图和局部放大图可见，随着倾角增大，油膜承载能力在整个表层渗透率变化范围内都增加.由图8(b)可见，随表层渗透率增加，油膜摩擦系数先迅速升高后趋于平缓，油膜摩擦系数与承载力的变化趋势相反，这符合一般实体轴承润滑理论的分析结果.在流体润滑工况下，压装在刚性轴承座中的轴承底面及两端面具有良好密封，在油膜压力驱动下接触面间的油液向轴承多孔基体中渗流.表层渗透率增加后，油液在油膜压力作用下更易向多孔基体中扩散，油膜压力变小，润滑性能变差(油膜承载能力降低，摩擦系数升高).图8(b)中的四条摩擦系数曲线存在近似的1个相交点，由局部放大图可见相交点对应的横坐标约为7×10−15m2.当表层渗透率小于7×10−15m2时，随着摩擦副间倾角增大，油膜的摩擦系数逐渐减小，当表层渗透率高于7×10−15m2时，随着摩擦副间倾角增大，油膜的摩擦系数逐渐增大.因此表层渗透率约为7×10−15m2是摩擦系数随倾角变化规律发生反转的突变点.这也验证了前述猜想.

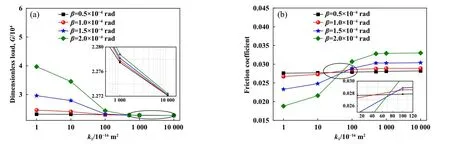
Fig.8 Loading capacity and friction coefficient of oil film under different surface permeability:(a) load capacity; (b) friction coefficient图8 不同表层渗透率作用油膜的承载能力和摩擦系数：(a)承载能力；(b)摩擦系数

分析可知，当表层渗透率较小时(小于7×10−15m2时)，含油轴承与常见实体轴承的润滑特性类似，增大摩擦副倾角后能使最小油膜厚度减小，接触面间的油膜动压效应增强，油膜的摩擦系数降低，油膜承载能力提高.当表层渗透率较高时(高于7×10−15m2时)，摩擦面间油液易向多孔基体中渗流，增大摩擦副倾角使得油液向多孔基体中的渗流效应进一步加剧，油膜压力向多孔基体中扩散较快，动压油膜部分卸压，导致油膜的摩擦系数升高.这与常见实体轴承的润滑特性不相符.

需要注意的是，当表层渗透率为1×10−13m2，含油轴承的两层渗透率相等，此时表示为普通单层含油轴承，当表层渗透率低于1×10−13m2，轴承是具有致密表层的双级孔含油轴承.当外界润滑供给充分或工况条件较好使得含油轴承处于流体润滑工况时，此时具有致密表层的双级孔含油轴承的润滑性能较单层含油轴承好(如图8所示，表层渗透率越小，摩擦系数越低).

2.2 摩擦表面上润滑油渗析特性分析

图9所示为不同倾角影响下轴承摩擦界面上的无量纲法向渗析速度.渗析速度指的是摩擦界面上润滑油向多孔基体渗入或从多孔基体向摩擦表面析出的流动速度.计算图9所示结果时取表层渗透率k1的值为1.25×10−14m2.在图9中，摩擦界面上法向渗析速度发生位置与油膜压力发生位置相同，均发生在收敛区间.法向渗析速度有正负之分，速度为正时，润滑油从摩擦界面向多孔基体渗入，速度为负时，润滑油从多孔基体向摩擦界面析出.在图9所示的4个倾角下，润滑油在环形接触区的收敛区间内总向多孔基体渗入，在紧邻渗入区的接触区入口位置润滑油向摩擦界面析出.显然可见，渗入区分布面积明显大于析出区分布面积，随着倾角增大，流体动压效应增强，流体的渗析速度峰值升高，渗析速度峰值发生位置在收敛区内逐渐向最小油膜位置靠近.

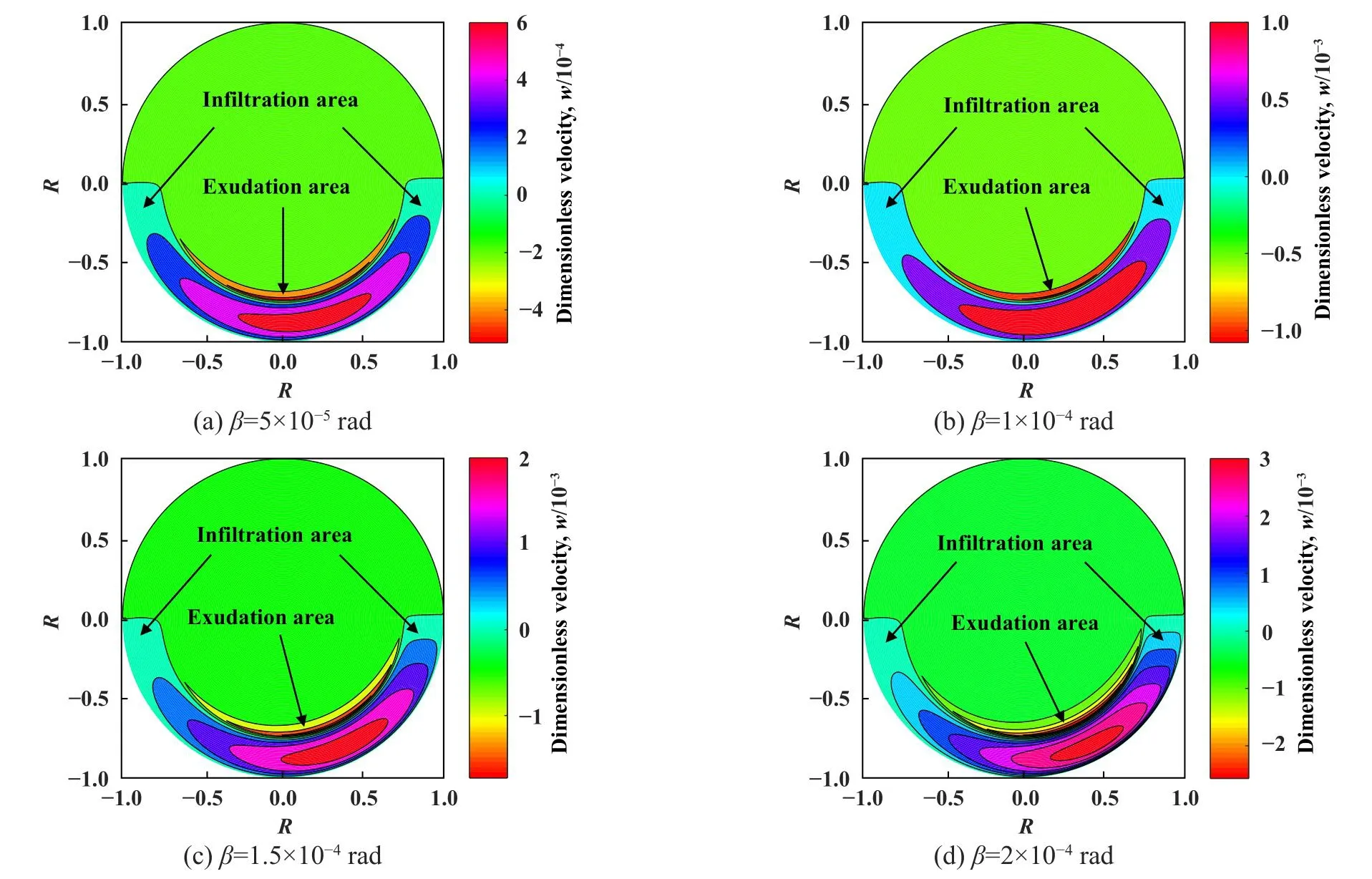
Fig.9 Normal dialysis velocity between ring-face friction pairs at different inclination angles图9 不同倾角作用下环-面摩擦副间的法向渗析速度

图10所示为倾角作用下摩擦界面上的无量纲法向速度.通过对比各倾角下的最大速度曲线可见，法向渗析速度在圆周方向上和径向上的分布均呈现与图9相似的规律.在周向上只存在渗入速度，渗入速度要分布在收敛区(π, 2π)，在径向上同时存在渗入和析出速度，渗入速度在接触区，析出速度在接触区入口部位.随着倾角增大，法向渗析速度在圆周方向上和在径向上均增大.

Fig.10 Dimensionless normal velocity at friction face under different inclination angles: (a) circumferential distribution of normal velocity; (b) radial distribution of normal velocity图10 不同倾角作用下摩擦界面上的无量纲法向速度：(a)法向速度沿周向的分布；(b)法向速度沿径向的分布

图11所示为不同表层渗透率影响下轴承摩擦界面上的无量纲法向渗析速度，其中倾角取值为2×10−4rad.在图11中，不同表层渗透率下，摩擦界面上法向渗析速度均发生在收敛区间.表层渗透率为1×10−16m2时，法向渗析速度分布较为集中，靠近最小油膜厚度位置.随着表层渗透率增大，法向渗析速度的分布逐渐变得均匀，法向渗析速度分布逐渐由最小油膜位置向整个收敛区间扩散.当表层渗透为1×10−12m2时，法向渗析速度分布在整个收敛区间内，基本沿收敛区中间转角3π/2位置两侧对称分布.与图9相似，油液渗入区的分布面积大于析出区分布面积，随着表层渗透率增大，多孔基体中油液的流动阻力减小，流体的渗析速度峰值升高.

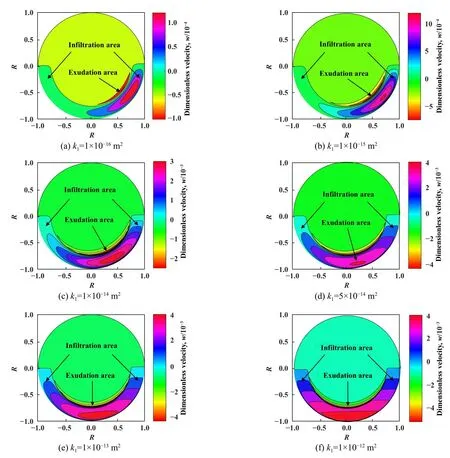
Fig.11 Normal dialysis rate between ring-surface friction pairs under different surface permeability图11 不同表层渗透率作用下环-面摩擦副间的法向渗析速度

图12所示为表层渗透率作用下摩擦界面上的无量纲法向速度.对比各表层渗透率下的速度曲线可见，法向渗析速度在径向上同时存在渗入和析出速度，渗入速度在接触区，析出速度在接触区入口部位.随着表层渗透率增大，法向渗析速度在圆周方向上和在径向上均增大.当表层渗透率增大到1×10−13m2后，渗析速度逐渐变得平稳.结合图8分析可知，当表层渗透率超过1×10−13m2后，润滑油膜的承载能力和摩擦系数也变得平稳.可见，含油轴承基体中油液的渗析速度变化较小时，润滑油膜处于平稳流动状态，油膜的承载能力和摩擦系数变化也不再发生显著变化.

Fig.12 Dimensionless normal velocity at friction interface under surface permeability: (a) circumferential distribution of normal velocity; (b) radial distribution of normal velocity图12 表层渗透率作用下摩擦界面上的无量纲法向速度：(a)法向速度沿周向的分布；(b)法向速度沿径向的分布

2.3 润滑与承载机理分析

当然，本文中研究所得结论是基于一定变化范围内的渗透率得出的.渗透率过小时，含油轴承接近不可渗透的实体轴承；渗透率过大时，轴承材料的力学性能变差，含油轴承不能适应工作要求，也就失去了研究的意义.综合上述分析，图13所示为倾角和一定变化范围内表层渗透率影响下环面摩擦副系统中的油液渗流扩散和润滑承载模型.在图13中，Q代表油液向多孔基体中的渗入量，G代表油膜的承载能力，f代表油膜的摩擦系数.由图13可知，在较小渗透率前提下，增大摩擦副间倾角对油膜的润滑性能有正反两方面影响：一方面由摩擦副间动压效应增强导致油膜的承载能力上升，摩擦系数降低；另一方面动压效应增强后使得油液向多孔基体的渗流扩散增加，摩擦界面油量减少，一定程度上削弱了动压效应.渗透率较小时，油液向多孔基体的渗流强度相对较低，故第二方面的作用较弱，第一方面的影响占主导，两方面综合影响的结果是增大倾角使得油膜的润滑性能变好(即油膜的承载能力上升、摩擦系数降低).

Fig.13 Oil seepage and lubrication model in porous bearing affected by inclination and surface permeability图13 倾角和表层渗透率影响下含油轴承油液渗流和润滑模型

在较大轴承渗透率前提下，摩擦副间动压油膜向多孔基体中的渗入量及压力扩散程度较高，含油轴承基体相当于1个容量远大于动压油膜体积的储油器.此时尽管增大倾角仍能改善油膜的润滑性能，但较高渗透率阻碍了倾角增大所致的润滑性能改善趋势.当渗透率足够大时，最终的结果是，增大倾角所致的油膜承载能力提升被成功阻止—承载能力几乎不再随倾角变化而变化，增大倾角所致的油膜摩擦系数变化发生反转—摩擦系数随倾角增大而增大.由此可见，油膜向多孔基体的渗入及压力扩散对油膜摩擦系数的影响要比对承载能力的影响大得多.