磁电弹性复合材料热接触特性研究
2023-06-05李玉堂周青华杨万友杨荣松
李玉堂, 周青华, 杨万友, 杨荣松
(1.四川大学 机械工程学院, 四川 成都 610065;2.四川大学 空天科学与工程学院, 四川 成都 610207)
作为智能材料的典型代表,磁电弹性(Magnetoelectro-elastic, MEE)复合材料由于其特有的压电和压磁效应可以实现电能、磁能和机械能之间的相互转化,可用于制造如压电/磁马达以及制动器等新型电机产品,在医疗器械等领域中应用潜力巨大[1-2].其中作为摩擦副的MEE材料由于摩擦力作用,在相对接触过程中将产生摩擦热.摩擦热载荷将导致MEE材料经历复杂热应力、热电和热磁响应[3-4],进而影响电机产品服役性能及寿命.因此,对MEE复合材料进行摩擦热接触建模,分析热载荷作用下材料多物理场响应和分布规律,将为有效掌握多重载荷作用下MEE复合材料接触性能演化规律奠定一定理论基础.
为了揭示这类复合材料的多物理场耦合效应,Wang等[5]推导了横观各向同性磁电弹性介质中三维通解,并给出了半空间磁电弹性介质多物理场求解Green函数.Ding等[6-7]推导了不同特征根下磁电弹性介质半空间基本解,给出了半空间表面单位点力、电和磁载荷作用下磁电弹性场的显式表达式.另一方面,Zhang等[8-9]在Ding给出的磁电弹性介质基本解[7-8]基础上引入快速傅里叶变换(Fast Fourier transform, FFT)和共轭梯度法(Conjugate gradient method, CGM),提出了一种求解磁电弹性材料三维接触问题的方法,并研究了多铁性薄膜与刚性绝缘球在表面磁弹性效应作用下的摩擦接触行为.此外,Chen等[10]推导了三种压头(平、锥及球形压头)压力与压痕深度的显式表达式,发展了磁电弹性复合材料的压痕理论.受摩擦热载荷或环境热载荷作用时,MEE材料会表现出热电性和热磁性,即材料受热膨胀产生的变形和温度变化会影响压电、压磁效应及其耦合机制[11-12].基于此,Chen等[13]推导了考虑热效应的磁电弹性复合材料三维多物理场通解,利用其求解了全空间磁电弹性材料在均布载荷作用下圆盘型裂纹应力、位移和磁感应强度因子.其后,不少学者针对MEE复合材料的层板和圆柱等基本结构体在外部力、电、磁和热载荷下的多场耦合现象进行了研究[14-16].然而,上述研究针对考虑热效应的MEE复合材料给出了多物理场通解,但并未详细推导热接触半空间条件下磁电热弹场的频率响应函数表达式,无法直接应用于考虑热效应的MEE复合材料接触建模.
本文中推导半空间表面单位集中法向力、切向力、电荷、磁荷和温升载荷作用下考虑热效应的MEE复合材料磁电弹热耦合场的频率响应函数,建立弹性球与MEE材料的滑动热接触半解析方法(Semi-analytical method, SAM)模型.模型充分考虑磁电弹性材料接触过程中摩擦热生成与分配及由其所致热电和热磁效应,并将模型计算结果与有限元方法(Finite element method, FEM)计算结果进行对比验证模型的有效性.最后,利用此模型研究不同滑动速度、摩擦系数和表面粗糙接触条件下,摩擦热效应对MEE复合材料应力、电势和磁势分布的影响规律.
1 问题描述和理论公式
1.1 考虑摩擦热效应的MEE复合材料接触模型
图1所示为笛卡尔坐标系中,法向载荷P作用下半径为R的MEE圆球在同质材料半空间表面以水平速度v沿x轴正方向滑动.其中,x-y平面与半空间表面重合,z轴垂直半空间表面并指向基体材料内部.球与表面滑动接触时,接触区会受到法向力pz和摩擦力px的作用,且px的大小由px=μpz确定(μ为摩擦系数).同时,接触区由于摩擦作用会产生热量(论文中假定热传导稳定时间比加载时间短得多,仅考虑稳态摩擦热作用),并假设稳态情况下摩擦损耗的能量完全转化为摩擦热并经接触区流入两个接触体,总摩擦热载荷为q=q1+q2= vμpz[17],q1和q2分别是滑动球和半空间的分得的热载荷.此外,假设半空间表面受分布电荷qb和磁荷gb作用.此时,在机械载荷(法向力pz和摩擦力px)、电荷qb、磁荷gb和热载荷q2四种载荷作用下,MEE复合材料半空间内部将发生复杂的磁电热弹性响应.
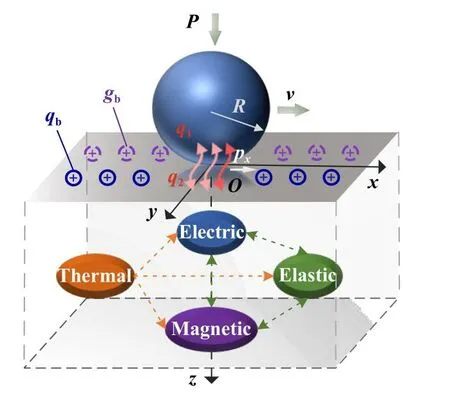
Fig.1 The thermal contact model of MEE composites图1 MEE复合材料热接触模型
MEE复合材料热接触分析流程如图2所示.初始化两接触体的表面形貌后,采用CGM[18]对下列载荷-位移平衡方程进行迭代求解,得到接触体表面的初始Hertz压力分布pz.
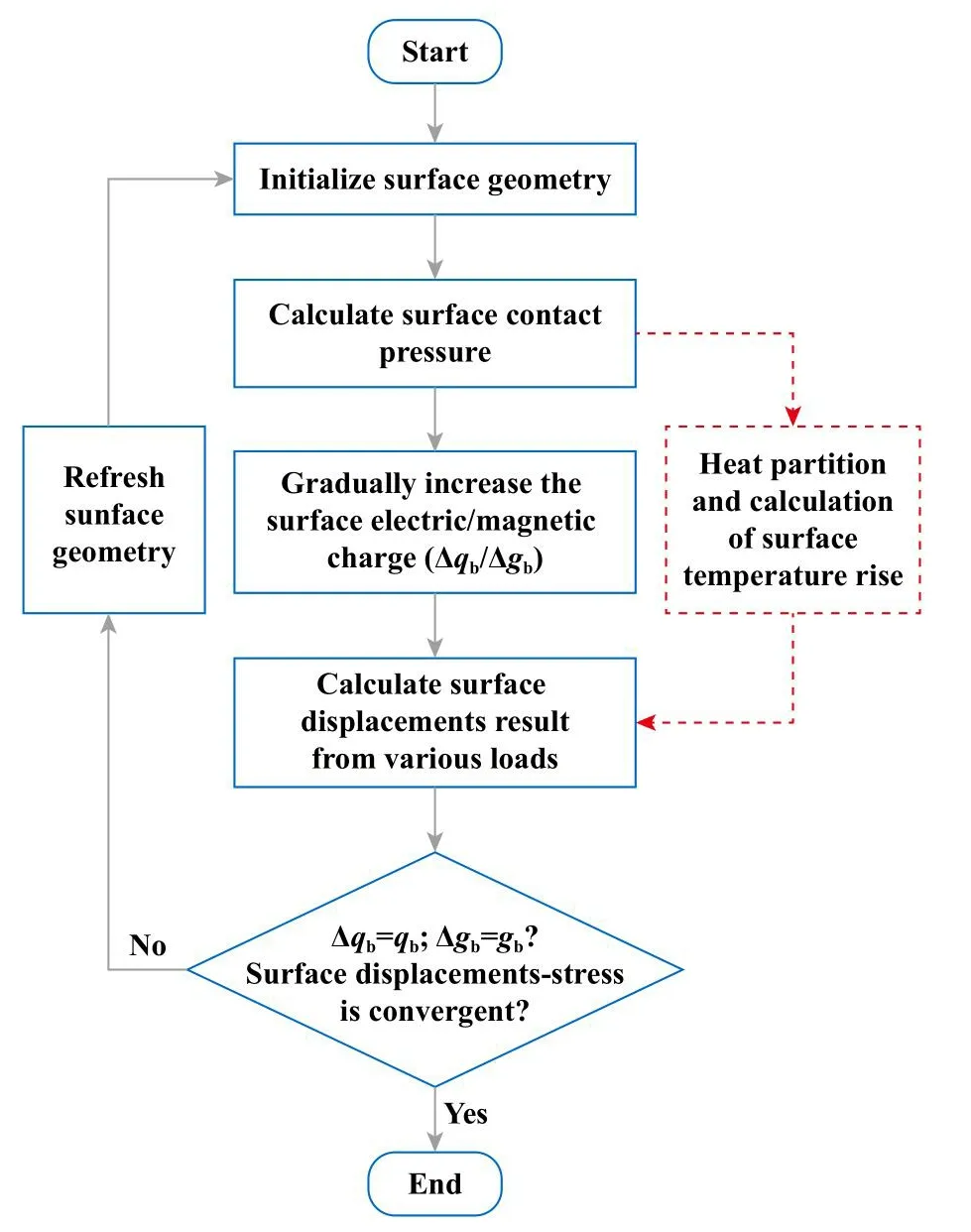
Fig.2 Flowchart of thermal contact solution method of MEE composites图2 MEE复合材料热接触求解流程图
其中,Ac为接触区面积,P为滑动球法向总载荷,hc为接触体之间的间隙,h0和δc分别是接触体之间的初始间隙和刚性位移,Qb和Gb分别为表面分布的电荷和磁荷总量,qb和gb分别是表面分布的电荷和磁荷,uz是表面力载荷、电/磁荷及热流作用下的法向变形.求得接触区分布压力后,进而计算摩擦热并对其进行热分配.热分配基于接触界面等温假设,其控制方程[19]可以写为
其中,∆T1和∆T2、q1和q2分别是球和半空间的表面温升和热载荷,|D1|和|D2|是两个接触体温升影响系数矩阵,{ }表示网格节点处热载荷或温升值的向量.式(2c)为线性方程组,只有q1是未知量,可利用共轭梯度法(Conjugate gradient method, CGM)求解得到q1和q2.此外,接触迭代求解过程中,在半空间表面逐次施加表面电荷∆qb和磁荷量∆gb[8],此处表面磁载荷gb和电载荷qb作为设定的输入条件,并假设其不会受热载荷改变的影响.根据界面载荷分布及大小计算表面位移及次表层变形和应力分布,然后将得到表面位移重新代入接触程序,重复上述过程至表面位移/应力收敛,表面电荷/磁荷累加至预设值,结束迭代并输出结果.计算流程如图2所示.
1.2 多重载荷作用下MEE材料物理场响应
1.2.1 基本方程与边界条件
在笛卡尔坐标系下,考虑热效应的横观各向同性(材料在与x-y平面平行方向为各向同性[13, 20])磁电弹性介质的本构关系为
其中,ux、uy和uz分别为x、y和z方向的位移;ϕ、φ和θ是电势、磁势和温升(θ= 0为参考温度);Dx、Dy、Dz和Bx、By、Bz表示电位移和磁感应;σx、σy、σz和τxy、τyz、τxz分别为正应力和剪切应力,cij、eij、qij、εij、dij、μij、p3和λ3(i,j=1, 2,···, 6)是弹性常数、压电常数、压磁常数、介电常数、电磁常数、磁导率、热电常数和热磁常数,并且2c66=c11−c12;β1、β2和β3是热应力系数.值得注意的是,横观各向同性材料中其与热膨胀系数α1、α2和α3有如下关系[21]:
没有外力和自由电荷的情况下,载荷平衡方程、麦克斯韦方程以及傅里叶稳态热传导方程为
其中,∧=∂2/∂x2+∂2/∂y2是二维Laplace算子,kij是热传导系数,Pe为佩克莱特常数,Pe=vl/γ,l为特征长度,γ为热扩散系数.
摩擦系数为μf的MEE复合材料半空间表面分布的载荷有法向力pz、摩擦力px、电荷qb、磁荷gb以及表面温升T,边界条件可以写作
1.2.2 频率响应函数
将本构方程(3)~(5)代入载荷平衡方程(7)、麦克斯韦方程(8)和傅里叶稳态传热方程(9),并引入位移函数ψ,通过算子理论可以从上述系列方程中得到如下通解[13]:
其中Ψ和F是两个中间函数,满足如下关系:
其中,zi= zsi(i=0,1,···,5)、al、bl、fl、gl(l= 1, 2,···, 4)和n0、n1、···、n4的表达式详见文献[16],si(i=1,2,…,4)是下列以s表示未知数的一元八次代数方程的4个实部为正的根.
按照文献[22]的方法求解方程(12)和(13)并代入式(11),可得一系列耦合场的频率响应函数.
将式(15)~(17)代入傅里叶变换后的边界条件(10),可得下列线性方程组:
求解线性方程组(18),可得待定系数A0、A1、···、A5,将其代入频域表达式(15)~(17)便得到位移、电势、磁势、应力、电位移和磁感应等物理量的频率响应函数.值得注意的是,由于通解(11)~(12)是在特征根si不同情况下成立的,所以若有特征根相同,需要按文献[13]所述方法重新设定位移函数进行推导.
为求解半空间接触体表面和次表面温升,还需引入热流-温升频率响应函数.对于稳态情况,Shi等[23]给出了横观各向同性材料半空间在热流作用下温升的频率响应函数
最后,将一系列频率响应函数转化为影响系数[8],以预设的表面电荷/磁荷(qb/gb)及表面力载荷(pz/px)、热流q2作为输入,可求解半空间表面/次表面的应力、温升、电势、磁势、电位移和磁感应等物理量.
1.2.3 影响系数
1.3 模型验证
为验证本文中提出模型的有效性,借助Abaqus商业软件,将模型计算结果与FEM结果进行比较.由于Abaqus软件中仅具有独立的压电和温度位移求解单元,所以将本文中所提模型退化至电-弹耦合解和热-弹耦合解.对于两种计算方法,在电弹耦合情况下,半空间接触体表面施加球形载荷其中r为接触半径,为最大压力值;在热弹耦合情况下,表面则施加球形热流q2=为最大热通量.对于本文中所提模型,总计算域设定为4r×4r×2r并离散成128×128×64个立方体单元.相应地,用Abaqus有限元软件轴对称建模方式,在同样载荷条件下建模计算,离散化的压电和温度位移单元网格数目为31 324.验证算例所选取材料的属性参数列于表1中.
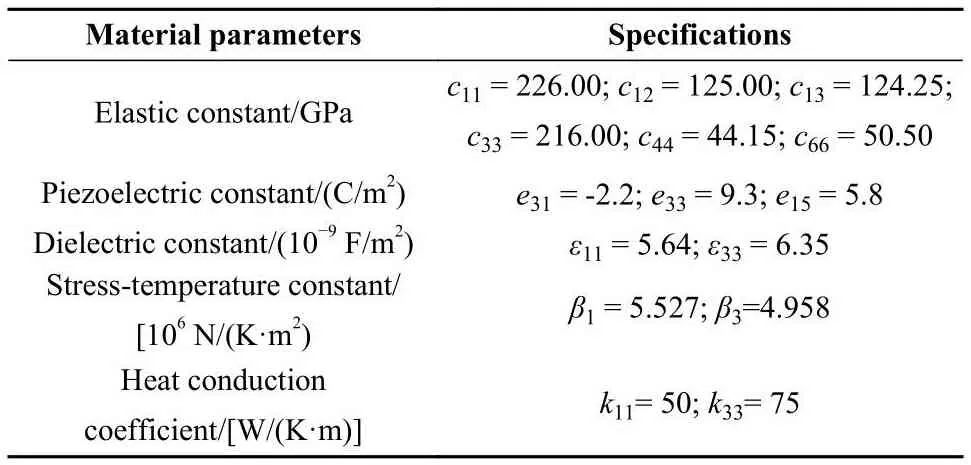
表1 模型验证中相关材料参数[24-25]Table 1 Material parameters in validation [24-25]
图3是电弹耦合情况下,利用本文中所提模型和FEM计算的接触体次表面von Mises应力和电势结果(电势量纲为最大压力值,e33为压电常数),由两种模型计算的应力及电势分布基本一致.进一步比较了接触体z轴方向上von Mises应力和电势分布,结果同样呈现出较好一致性.热弹耦合情况下两种模型计算的相应结果如图4所示(图中σvm、ϕ和r表示von Mises应力、电势和接触半径),结果显示两种模型计算结果同样较为接近.因此,通过上述算例结果验证了本文中所提模型的有效性.

Fig.3 Subsurface stress and electric potential computed by the SAM and FEM图3 由所提SAM及FEM计算得到的次表面von Mises应力和电势分布
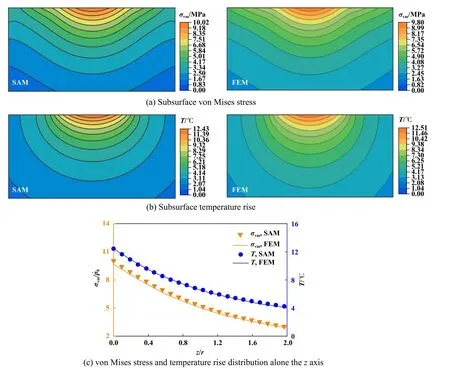
Fig.4 Subsurface stress and temperature rise computed by the SAM and FEM图4 由所提SAM及FEM计算得到的次表面von Mises应力和温升分布
2 摩擦热载荷对MEE材料接触行为影响分析
设半空间表面分布有均匀电荷qb= 0.001 C/m2、磁荷gb= 0.001 N/(A·m),MEE球在法向载荷P=P0和滑动速度v=v0作用下与MEE半空间接触.模型算例网格设置与上节相同,并选取典型MEE材料BaTiO3-CoFe2O4为研究对象,其材料参数列于表2中.

表2 BaTiO3-CoFe2O4材料参数[23-24]Table 2 Material parameters of BaTiO-CoFeO[23-24]324
2.1 滑动速度
滑动速度v是决定摩擦热载荷(q=pzμv)的重要因素.设滑动速度v以v0为增量,从0到4v0之间变化,摩擦系数μ设定为0.1,利用MEE复合材料摩擦热接触模型研究不同速度对其次表面磁电热弹性场的影响.图5所示为不同滑动速度时MEE复合材料温升及应力分布(图中T0为v = v0时材料表面最大温升).随着滑动速度增大,MEE复合材料次表面的温升逐渐增大,越靠近接触区表面温升越高[图5(a)].结合图5(b)可知,在球滑动方向后端的摩擦热温升较高,而滑动方向前端的温升较低,且温升最值向着球滑动的反方向偏移,与文献[19]所得规律一样.在滑动方向后端的这类温升较高区域中,在滑动速度v<2.5v0时,总应力逐渐减小,而后随着v增大,总应力有较小增大趋势,von Mises应力分布集中的区域也向着滑动方向前端移动,如图5(c)所示.图5(d)进一步示出了滑动速度变化时,MEE复合材料内最大von Mises应力σvm, max及其对应x轴坐标的统计结果.结果显示,滑动速度越大,σvm, max逐渐减小且位置向球滑动方向偏移,印证了图5(c)所得结论.

Fig.5 Temperature rise and stress distribution of the MEE contact body applied with different sliding speeds图5 不同滑动速度时MEE材料次表面/表面温升和von Mises应力分布
图6(a)所示为不同滑动速度时,热接触载荷下MEE次表面电势分布(图中ϕ0为v=v0时材料表面最大电势).结果表明,热效应对MEE复合材料电势分布影响与应力类似,即随着滑动速度增大,靠近接触区表面温升较高的区域电势逐渐减小.图6(b)中展示的表面电势分布同样可以看出,滑动速度越大,即温升越大,电势反而越小,说明温升与电势成负相关关系.不同滑动速度下MEE复合材料次表面和表面磁势分布如图6(c)和(d)所示(图中φ0为v=v0时材料表面最大磁势),在当前滑动速度范围内,由于滑动速度变化导致的热效应差对材料磁势影响较小,仅在接触区及附近区域磁势有较小幅度的增加.

Fig.6 Electric and magnetic potentials of the MEE contact body applied with different sliding speeds图6 不同滑动速度时MEE复合材料次表面/表面电势和磁势分布
2.2 摩擦系数
保持滑动速度v=v0不变,摩擦系数从0到0.4变化时MEE复合材料次表面/表面温升和von Mises应力分布情况如图7所示.摩擦系数增大将产生较高的表面热流,进而使MEE复合材料次表面和表面温升增大.与改变滑动速度算例[图5(a)和(b)]不同的是,单纯摩擦系数增大只引起了温升数值的变化而并未改变温升分布规律.图7(c)和(d)结果表明,摩擦系数增大,主要应力集中区域逐渐沿球滑动方向移动并靠近表面,该结论与文献[26]中纯弹性材料以及文献[27]圆柱与半空间接触结论一致,并且当摩擦系数增大到一定数值(约为0.2),最大von Mises应力σvms, max在水平方向的偏移达到极限.σvms, max随着摩擦系数增加先减小后增大,该结论与文献[26]中纯弹性材料σvms, max随摩擦系数一直增大不同,这表明考虑接触热影响的情况下,摩擦系数较小时产生的热膨胀应变在应力分布中起主导作用,而不是机械载荷产生的压应变.
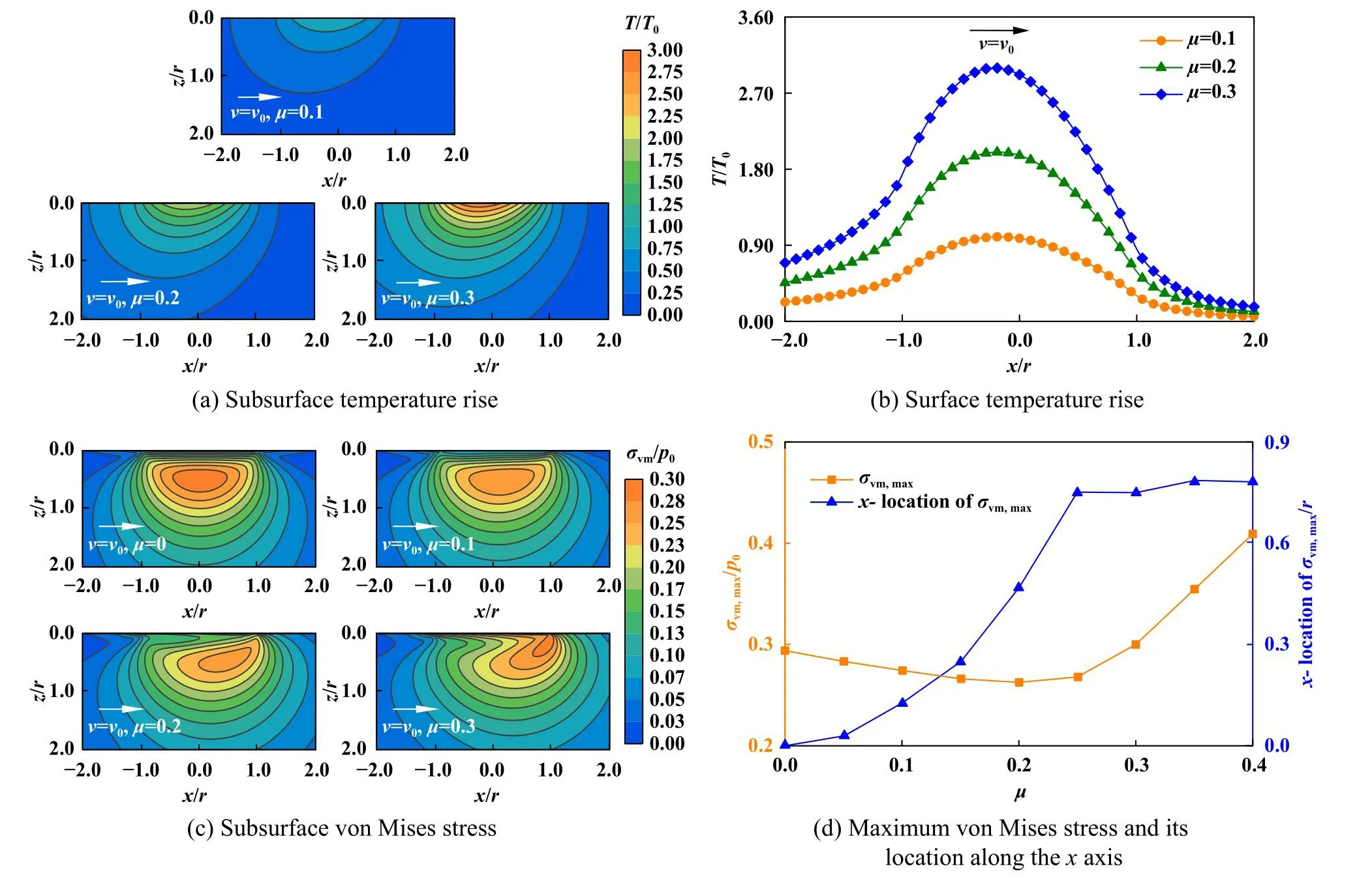
Fig.7 Temperature rise and stress of the MEE contact body applied with different friction coefficients图7 不同摩擦系数时MEE材料次表面/表面温升和von Mises应力分布
不同摩擦系数作用下MEE复合材料电势和磁势分布如图8所示.当摩擦系数增大时,由于温升增大,MEE复合材料次表面电势数值逐渐减小[图8(a)].与改变滑动速度时不同,摩擦系数的改变还引起了表面摩擦力的变化,使得电势沿滑动反方向的偏移更加明显,如图8(b)所示.磁势分布计算结果显示[图8(c)和(d)]与电势分析结论不同,摩擦系数越大,靠近接触区表面的磁势缓慢增大.然而受摩擦力变化影响,表面磁势沿滑移方向偏移并不明显,与上节中滑动速度分析结果较为一致.
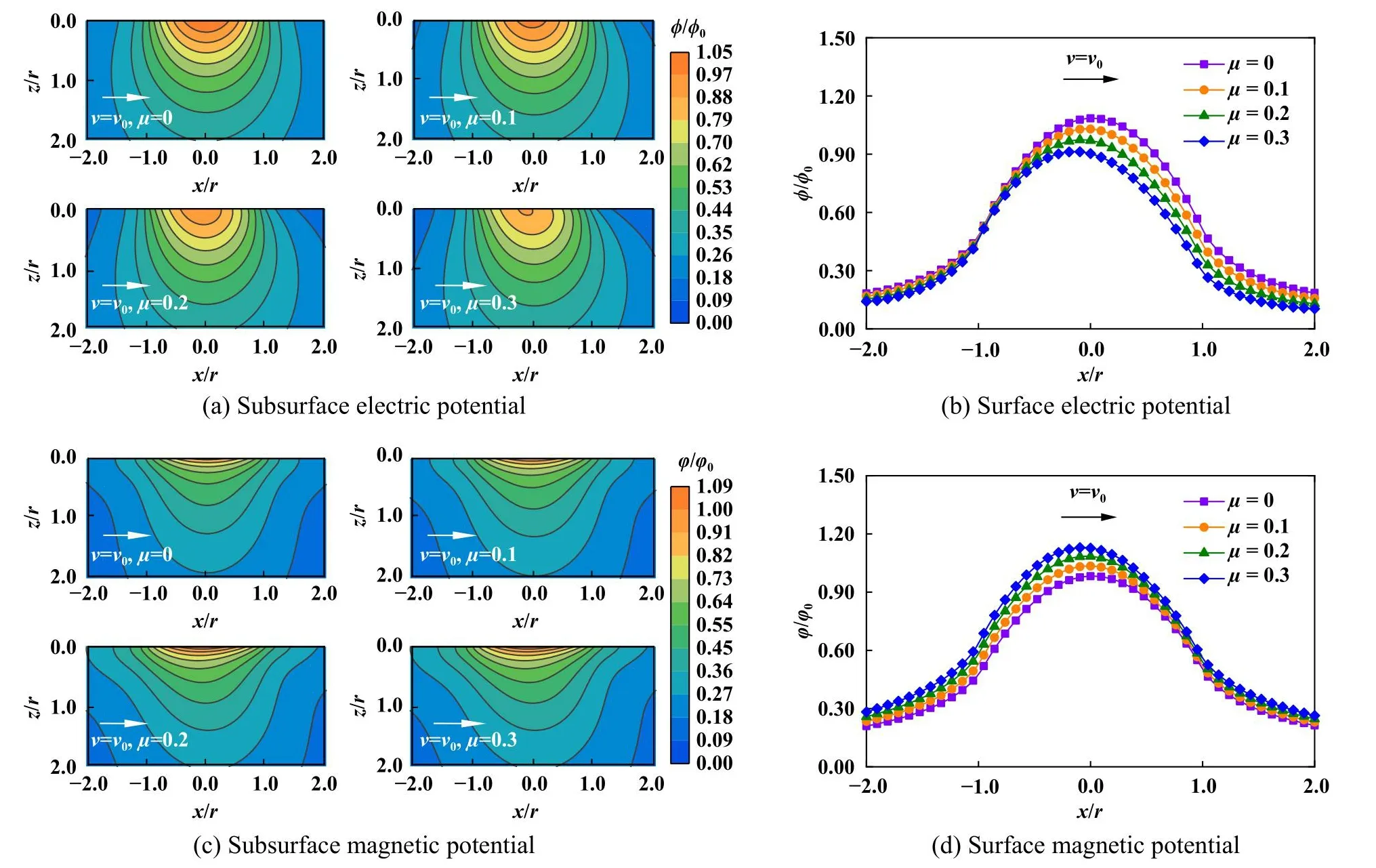
Fig.8 Electric and magnetic potentials of the MEE contact body applied with different friction coefficients图8 不同摩擦系数时MEE材料次表面/表面电势和磁势分布
2.3 粗糙表面接触
为模拟粗糙表面接触,在光滑半空间表面施加正弦波粗糙轮廓.设正弦波粗糙表面的轮廓为z=cos(2.5πx)cos(2.5πx)×0.001r,保持摩擦系数μ= 0.1和滑动速度v= 4v0不变,探究MEE复合材料在粗糙表面接触时,摩擦热对应力、电势和磁势的影响.图9(a)所示为考虑摩擦热影响时,MEE复合材料温升和表面压力分布,粗糙表面接触改变了接触区的形状和面积,接触点处集中的表面压力产生了更大的表面热流,使得接触点处温度明显升高,该现象与文献[28]的瞬态热力耦合分析结果一致.图9(b)中对比了平整和粗糙表面接触的次表面温升分布,结合图9(a)可以看出粗糙表面接触时,表面压力集中的接触点附近温升较高.图9(c)中结果显示,von Mises应力受集中分布表面压力的影响,也集中于接触点区域.在考虑摩擦热影响后,次表面的von Mises应力减小,并且滑动速度后端接触点处温升更高,von Mises减小明显.
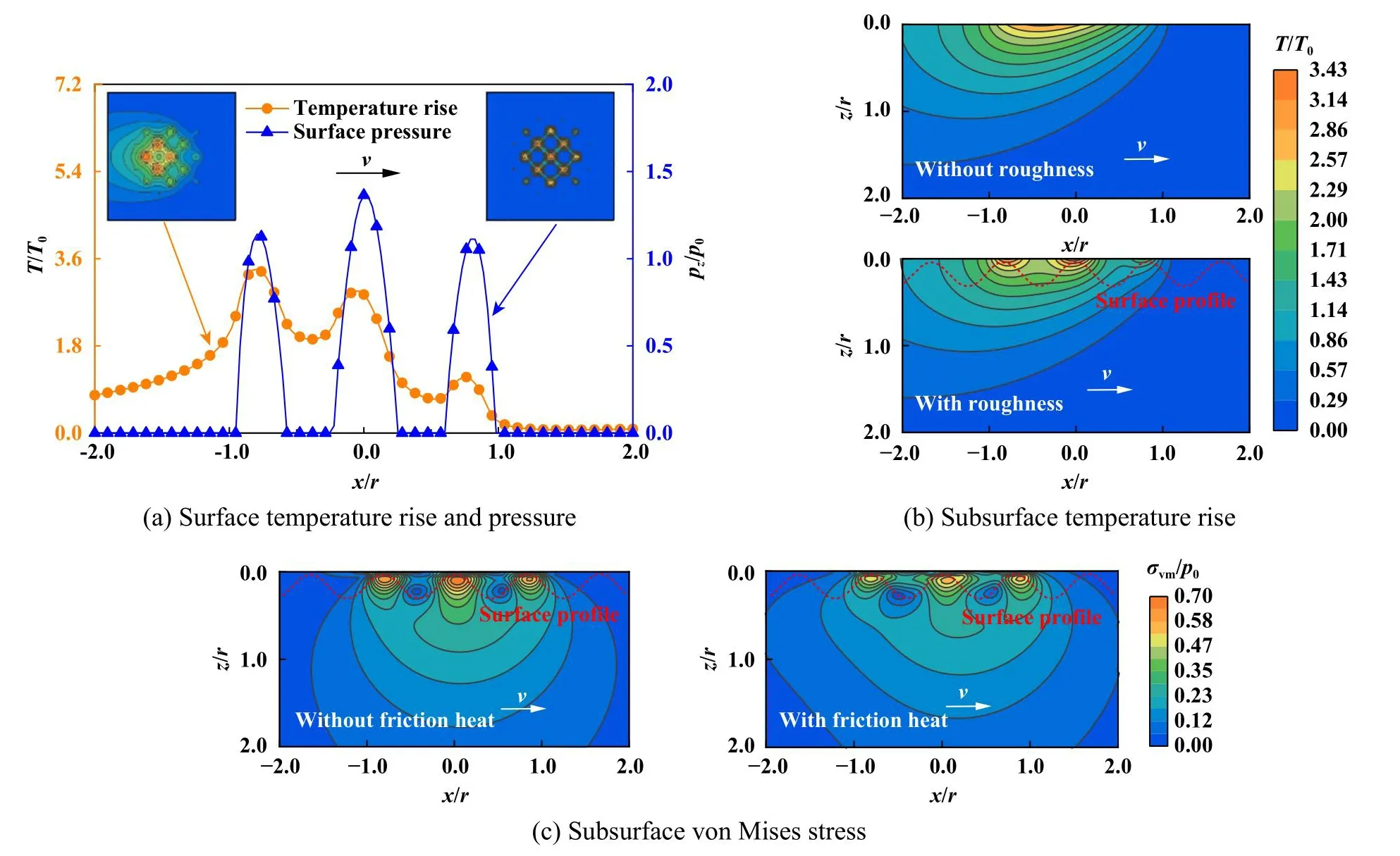
Fig.9 Temperature rise, surface pressure and stress of the MEE contact body of rough-surface considering frictional heat or not图9 考虑/不考虑摩擦热情况下粗糙表面MEE复合材料温升、应力和表面压力分布
图10所示为忽视及考虑摩擦热情况下,MEE复合材料粗糙表面接触电势和磁势分布.由于接触压力趋于集中,电势和磁势同样集中分布于接触点附近.考虑摩擦热影响后,电势减小,特别是位于滑动方向后端的接触点,由于其临近区域温升较高,电势减小更为显著[图10(a)].结合图10(b)可知,受摩擦热影响后表面电势减小,并且球滑动方向的接触点电势高于后方.与此同时,图10(c)和10(b)的结果表明磁势受摩擦热影响分布变化不大,表面磁势略有增加,滑动方向后端温升较高的接触点磁势高于前端.
2.4 各物理场的温度敏感性
为探究弹性场、电场和磁场的温度敏感性,以法向载荷P=P0,滑动速度v=v0,摩擦系数μ=0.1条件下产生的表面温升T0为参考值,定义步长为0.1T0时各物理场温度敏感性函数S(T)为[8]
其中,V为接触中心弹性场、电场和磁场的接触行为,包括法向位移uz、电势ϕ和磁势φ.各物理场对表面温升的敏感性如图11所示,可以看出,各物理场受表面温升影响的敏感程度由高到底排序依次是弹性场、电场和磁场.
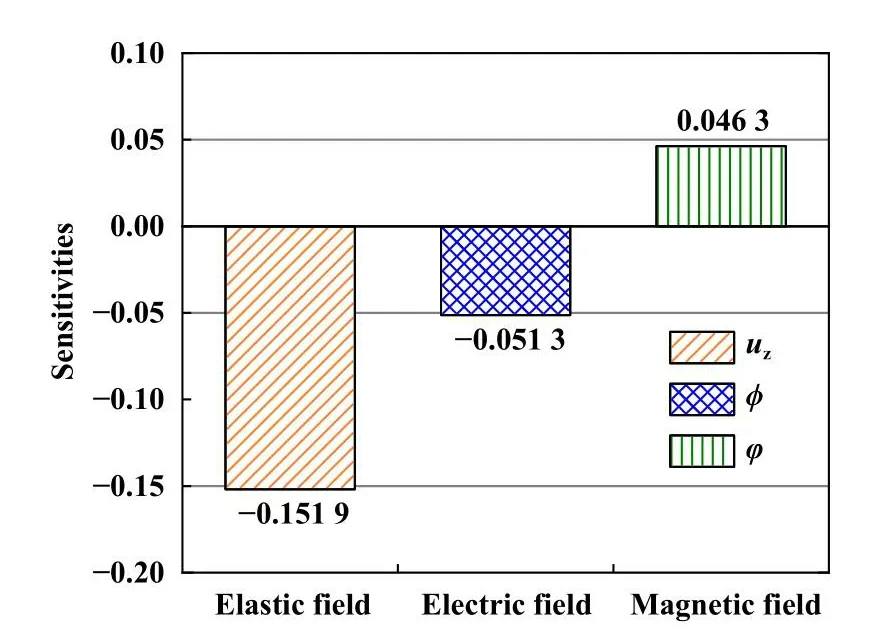
Fig.11 Sensitivities of each physical field to surface temperature rise图11 各物理场对表面温升的敏感性
3 结论
a.本文中推导了考虑热效应磁电弹性复合材料的频率响应函数,引入热流-温升影响系数计算摩擦热产生的温升,建立了MEE材料摩擦热接触半解析模型,采用离散卷积快速傅里叶变换和共轭梯度法加速计算,并与有限元分析结果对比,验证了模型的有效性.
b.随着滑动速度增大,MEE复合材料接触区和滑动方向后端温升增加,von Mises应力先逐渐减小后有缓慢增加的趋势,且应力集中区向着球滑动方向移动;靠近接触区电势减小,且其分布向球滑动方向出现偏移.滑动速度改变对磁势影响不大,接触区附近磁势略微增加.
c.随着摩擦系数增大,MEE材料接触温升增大.最大von Mises应力先减小后增大,并且向表面和球滑动方向移动.电势减小,偏移现象更加明显.接触区附近磁势小幅增加,同时在球滑动反方向上出现偏移.
d.考虑表面粗糙属性时,MEE材料的温升、电势和磁势倾向于向表面接触点附近集中.考虑摩擦热影响后,球滑动反方向区域的接触点温升较高,von Mises应力和电势减小,而磁势有小幅增加.
f.在摩擦接触中,各物理场受温升影响的敏感程度由高到低为弹性场、电场和磁场.
附录:
第1.2.2小节式(15)~(17)中的系数表达式如下:
