简单随机抽样中的交互回归估计及其应用
2023-06-04刘高生赵静文
刘高生,曹 琴,赵静文
(1.天津商业大学 理学院,天津 300134; 2.天津城建大学 经济与管理学院,天津 300384)
0 引言
大数据具有免费获取、数据量大等优点,但如果对大数据直接进行分析,不仅数据量庞大、耗时长,且计算效率低。面对如此庞大的数据,需要运用抽样技术进行样本选取,抽取一部分与总体研究对象高度相关的样本量进行分析,根据调查数据,对全体对象进行推断、估计。目前,抽样调查被广泛应用于各个领域,需进一步研究如何选择合适的抽样估计方法,达到更好的抽样估计效果。
国外对抽样调查方法的研究可追溯到19世纪。Kiaer提出了“代表性抽样”概念,即从总体中抽出一组可代表该总体的样本。Neyman、Hansen及Mahalanobis等进行了进一步的研究,提出了更加完整的抽样调查方法理论体系。1980年,Metrika对简单估计、比率估计等估计方法的性能进行了研究。20世纪初,Horviz和Thompson提出了无偏估计理论,抽样调查方法的理论体系日趋完善。
国内关于抽样调查的理论及方法日益丰富。孙山泽[1]等、金勇进[2]等对7种主要调查方法的公式推导进行了研究,给出了这些理论的应用条件及方法。卢宗辉[3]等提出了基于对等概率和不等概率不同抽样方式下抽样方差的计算与比较,研究发现,不等概率抽样比率估计比等概率抽样比率估计效果更好。邓明[4]等阐述了基于比率估计的抽样方法对复杂的时间序列数据季节指数的估计,解决了季节指数对观测期数要求高的问题。俞纯权[5]讨论了有辅助变量可利用时估计量的选择问题。乔松珊[6]等利用多辅助信息构造了比率估计。卢玉桂[7]等提出了基于R软件利用分层抽样方法,解决完整抽样框和非完整抽样框两种不同情况下样本选取及对总体参数的估计。贺建风[8]等提出了基于大数据将切片逆回归得到的综合得分作为辅助变量来构造概率,利用不等概率抽样获得了更好的抽样估计效果。
当抽样调查中存在辅助变量,且与目标变量存在一定的线性关系时,为估计总体均值,传统的抽样理论方法一般考虑回归估计,但回归估计仅考虑了一个辅助变量的情况,而当抽样调查中存在多个辅助变量时则无法有效应用。为充分利用变量间的交互信息,将其扩展到多个交互辅助变量的情况,提出了多元交互回归估计。在模型中加入交互效应,不仅可提高模型的解释能力,还能深入研究交互效应变量,这种类似交互式回归的思想可参考文献[9-10]。本研究运用数据可视化的方式,将不同抽样估计方法下复杂的理论结果用图形直观呈现出来,并对不同抽样估计方法进行比较分析,为实际调查研究提供了一定的方法参考。
1 多元交互回归估计
在简单随机抽样方法中,估计总体均值常用的估计方法为简单估计(y.bar)、比率估计(y.R)及回归估计(y.lr)等。其中,简单估计是用样本均值作为总体均值的估计。当抽样调查过程中存在与主要目标变量相关的辅助变量时,通常可以考虑利用这些辅助变量信息来提高估计值的精度。而比率估计和回归估计只考虑了一个辅助变量的情况,考虑到抽样调查的指标信息中可能存在多个辅助变量,故而提出了多元交互式回归估计(y.lrm)。

若得到的新的辅助变量很多,且存在很多对因变量不显著的变量,可通过Lasso筛选变量的方法去掉不显著的变量,如果这些新的辅助变量之间存在一定的相关性,可利用主成分降维法得到不相关的主成分,将得到的主成分及其交互项作为新的辅助变量。
设研究的总体指标量为Yj,Xij(i=1,2,3,…k;j=1,2,3…N),从总体中抽取n个简单随机样本,记为:yj,xij(i=1,2,3…k;j=1,2,3…n)。
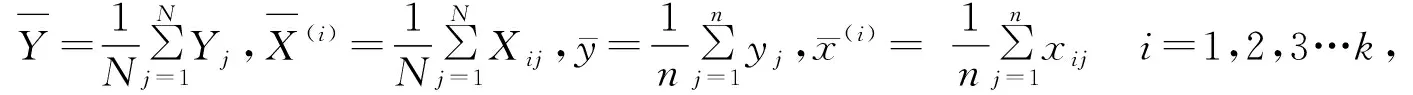

则多元交互样本回归系数bi(i=1,2,3…,k)可取以下向量的第i个值;
b=(x′x)-1x′y;
综上,多元交互回归估计的理论如下:
(1)
多元交互回归估计的均方偏差的估计为:
(2)

2 Bootstrap方法估计方差的过程
由于多元交互回归估计的方差的估计计算公式较为复杂,提出Bootstrap方法估计多元交互回归估计的方差过程,基本过程如下:步骤1:从总体中抽取n个原始样本,采用重抽样技术从原始样本中重复抽取m次产生一定数量的再生样本,此过程允许重复进行,设定m=300次。步骤2:根据步骤1中抽取的再生样本结果,计算出多元交互回归估计值。步骤3:将步骤1、2、3重复执行m次,即可得到m个多元交互回归估计的估计值。步骤4:基于步骤3的计算结果,计算出这m个多元交互回归估计值的方差,即为利用Bootstrap方法给出的多元交互回归估计方差的估计。Bootstrap方法估计方差步骤如图1所示。
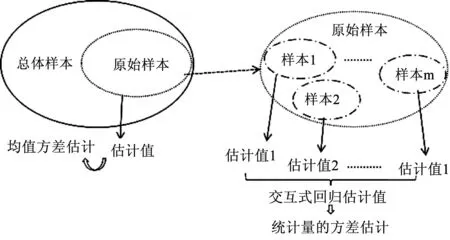
图1 Bootstrap方法估计步骤示意图Fig.1 Step diagram of Bootstrap method estimation
3 模拟研究
数值模拟的数据集从线性回归模型Y=0.5X1+0.5X2+0.5X1*X2+e中产生,其中X1服从二项分布为B(1,0.5),X2服从正态分布N(1,1),误差项e服从正态分布N(0,σ2)。多元交互回归估计以X1、X2、X1*X2为3个辅助变量,比率估计及回归估计以X1为辅助变量。
从N=800的总体体中抽取n个样本,误差项的方差设定分别为σ=0.1、σ=0.5。运用简单估计、比率估计、回归估计及多元交互回归估计4种方法估计总体均值。当误差项方差改变时,对比分析不同的估计方法对总体均值的估计。设定样本量n=100,试验重复抽取m=300次,得到4种估计的箱线图如图2所示。
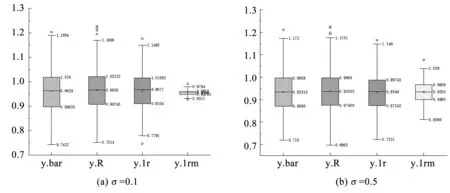
图2 样本均值估计箱线图Fig.2 Box plot of sample mean estimation
在无偏估计的条件下,抽样调查方法模型的均值估计量越集中,则估计方差越小,估计效果越好。从图2可知,当固定样本量,误差项方差变大时,4种估计的四分位差都变大,估计效果都变差。当固定误差项方差时,简单随机抽样中的简单估计的四分位差较大,估计效果较差,比率估计与回归估计四分位差相差不大,估计效果相差不大,而在回归估计的基础上提出的多元交互回归估计的四分位差最小,估计效果较好。
对模拟数据集抽取n1=100、n2=200、n3=300、n4=400的样本,对比探究估计量的偏差及方差变化。利用Bootstrap方法,重复抽取m=300次,在σ=0.5的情况下得到这4种估计方法的估计偏差折线图如图3所示。

图3 估计偏差折线图Fig.3 Line plot for estimating deviations
由图3可知,这4种估计的偏差都较小。当n=100、200、300时,简单随机抽样中的简单估计的偏差估计小于比率估计与回归估计的偏差估计,而当n=400时,比率估计与回归估计的偏差估计均小于简单估计的偏差估计,而多元交互回归估计在任何样本情况下的偏差估计量都是最小的。
由图4可知,固定估计方法随着样本量的增加,估计方差在减小,估计精度随之提高,当n=400时,估计方差是最小的。在固定样本量时,简单估计的方差最大,比率估计与回归估计的估计方差相当,多元交互回归估计的估计方差最小,估计效果最好。简单估计的估计效果最差,主要是因为简单估计没有利用辅助变量信息,而比率估计、回归估计及多元交互回归估计利用了辅助变量信息,从而提高了估计精度。比率估计与回归估计利用了一个辅助变量,估计方差比简单估计要小,而多元交互回归估计利用了多个辅助变量及交互信息,估计方差最小,估计效果最好。
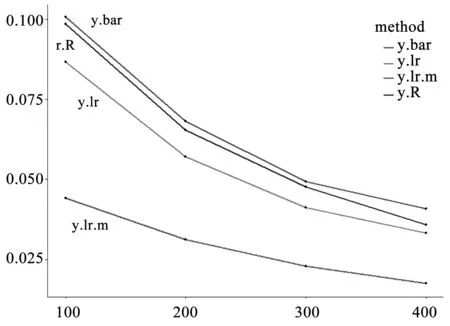
图4 Boostrap方法得到的方差估计折线图Fig.4 Line chart of variance estimation gained by Boostrap
图5给出了不同方法下方差的估计条形对比图,蓝色表示利用Bootstrap方法得到的估计均值算出的方差的估计,绿色表示利用估计方法的计算公式得到的方差的估计。将运用Bootstrap方法对方差进行估计的结果与传统公式计算方差的估计结果进行比较可知,两种估算方法下的估计方差都随着样本量的增加而减小,当样本量很大时,两种方法得到的方差估计大致相等,这说明利用Bootstrap方法对均值方差进行估计所得的结果是合理有效的,可弥补传统抽样理论中方差估计计算复杂的缺陷,对抽样方法理论及实际应用具有一定的意义。

图5 方差的估计条形对比图Fig.5 Bar comparison chart of variance estimation
4 实证分析及结论
实例分析使用的数据集为Bike Sharing Dataset[11],包括N=731条观测数据,变量数目为7个,其中包括6个自变量、1个因变量。各个变量的指标含义如下:workingday-(X1)工作日,weathersit-(X2)天气情况,temp-(X3)温度,atemp-(X4)体感温度,hum-(X5)湿度,windspeed-(X6)风速,cnt-(Y)共享单车租赁数量。
对变量进行相关分析可知,温度、体感温度与共享单车租赁数量相关系数接近0.6,天气情况、湿度、风速等研究变量都与共享单车租赁总数有一定的线性相关性,但是相关性较弱,而工作日的相关性程度最弱。为避免辅助变量间存在多重共线性,选择体感温度和天气情况作为辅助变量。为估计共享单车租赁数量的均值,比率估计及回归估计只利用体感温度这个辅助变量,而多元交互回归估计利用体感温度、天气情况及交互信息作为辅助变量。
从N个总体中随机抽取样本量分别为100、400的样本,重复抽取300次,采用简单估计、比率估计、回归估计及多元交互回归估计方法估计共享单车租赁数量的均值,得到不同样本量情况下估计量的箱线图如图6所示。
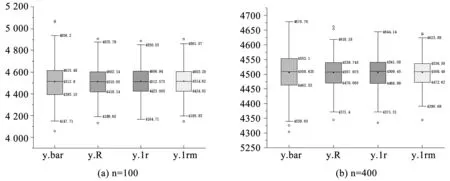
图6 均值估计箱线图Fig.6 Box plot of mean estimation
由表1、表2可知,随着抽取样本量的增加,这4种估计的方差都在减少。在固定样本量的条件下,简单估计的四分位距最大,多元交互式回归估计的四分位距最小,比率估计和回归估计的四分位距相差不大,说明提出的多元交互回归估计在实际数据中估计效果较好。随着抽取样本量的增加,几种方法得到的估计异常值有所增加,且数据异常值正负都有,这是由于样本均值在样本量很大的情况下服从正态分布导致的,结果合理。

表1 n=100的均值估计Tab.1 Mean estimation of n=100
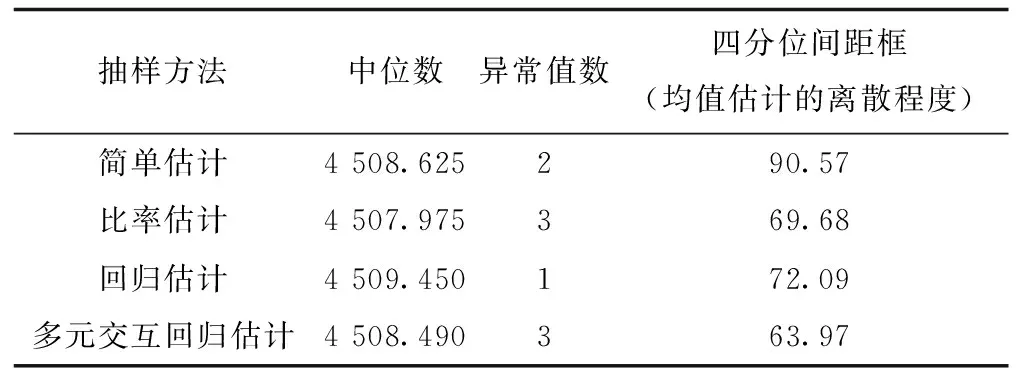
表2 n=400的均值估计Tab.2 Mean estimation of n=400
