建筑外墙延迟衰减特性的组合优化方法
2023-06-03杨昌智陈王小琛
杨昌智,陈王小琛
(湖南大学 土木工程学院,湖南 长沙 410082)
在全球能源消费中,建筑领域能耗约占36%[1].2019 年我国建筑全过程能耗总量为22.33 亿t 标准煤,占全国能源消费总量的45.9%[2],降低建筑能耗也因此成为解决能源短缺问题的重要途径[3].空调系统能耗占建筑总能耗的50%~70%[4-5],其中大约有30%~50%被围护结构传热产生的冷/热负荷所消耗[6].因此,进行围护结构节能研究对降低建筑能耗具有重要意义.
在外扰作用下,墙体实际传热呈非稳态变化,即影响墙体传热的参数不光有导热性,还包括蓄热性[7].蓄热性是指外墙在其表面温度或热流波动作用下吸收热量的性能[8],在蓄热性的影响下,墙体内表面峰值温度出现时间会有所延迟,内表面温度波幅会发生衰减,由延迟时间与衰减倍数来量化影响程度.内表面峰值温度是计算墙体峰值传热量的重要参数,峰值传热量则是构成建筑围护结构峰值冷负荷的主要部分.在夏季,极端气候周期较短,空调系统不会长时间处于额定工作状态,若峰值冷负荷过大导致空调设备选型过大,则不仅会影响初投资与后期的维护成本,还会产生系统运行能效降低等问题[9-10].因此,研究延迟衰减特性与墙体峰值传热的关系对实现建筑节能具有重要意义.
目前,利用延迟时间与衰减倍数评价新型墙体的热物性[11-12]、探究不同因素对墙体延迟时间与衰减倍数的影响[13-14]和研制新型材料以提高墙体延迟衰减特性[15-16]等是主要研究方向.上述研究中,延迟时间与衰减倍数主要作为目标优化参数或评价指标,而直接利用延迟衰减特性进行建筑能耗分析的相关研究还较少.由于墙体延迟特性不能改变墙体传热量的大小,多种墙体之间不同延迟时间的比较无法得出延迟时间与峰值传热的相关结论,因此采用墙体组合的形式对延迟特性进行研究.
本文基于谐波反应法,介绍了延迟衰减参数与墙体传热量的关系.构造延迟衰减特性不同的墙体,利用正交试验设计方法得出多种墙体组合,采用EnergyPlus对各墙体组合进行模拟,研究墙体组合延迟衰减特性对建筑峰值传热冷负荷的影响.根据结论,提出一种基于墙体组合延迟衰减特性的外墙峰值传热优化方法,以期对建筑蓄热设计提供参考.
1 延迟衰减特性与墙体传热
1.1 墙体传热的延迟时间与衰减倍数
延迟时间与衰减倍数是墙体蓄热能力的表征参数.室外空气综合温度与墙体内表面温度的波幅之比为衰减倍数ξ,衰减倍数越大,墙体对外扰波幅的削减就越大;室外空气综合峰值温度与墙体内表面峰值温度的出现时间之差为延迟时间φ,延迟时间越大,外扰峰值进入室内的时间就越长.
式中:Asa与Ain分别为室外空气综合温度与墙体内表面温度的波幅,℃;与分别为室外空气综合温度的最大值与最小值,℃;与分别为墙体内表面温度的最大值与最小值,℃;与分别为室外空气综合峰值温度与墙体内表面峰值温度的出现时间,h;P为时间周期,h.
室外空气综合温度是在室外空气温度的基础上加上了当量太阳辐射强度的“等效温度值”,计算式如下:
式中:tout,air为室外空气温度,℃;a为墙体外表面太阳辐射吸收率;I为太阳辐射总强度,W/m2;αout为外表面对流换热系数,W/(m2·K).
1.2 墙体传热计算
谐波反应法是计算墙体非稳态传热的经典方法,其特点是:对室外边界条件利用傅氏变换,将周期性非简谐温度波转换为周期性简谐波[17].根据 式(3)求出室外空气综合温度逐时值曲线,利用傅氏变换分解曲线,得到室外空气综合温度傅氏级数展开式:
式中:A0为室外空气综合温度平均值,℃;An为第n阶外扰的振幅,℃;ω为外扰频率,ω=π/12;φn为第n阶外扰的初相位,rad;n为外扰阶数,一般取3阶即可满足工程精度;τ为时间变量.
谐波反应法计算墙体传热中很重要的一环在于求解墙体对各阶外扰的频率响应,即延迟时间与衰减倍数.设室内温度恒定,采用传热频率响应计算.根据式(4),设外扰为周期性正弦波,即正弦波频率为ωn,振幅为An,初相位为φn,则式(5)中的虚部表示墙体输入的温度波:
式中:C(s)为系统输出函数;H(s)为传递函数;R(s)为系统输入函数.
根据板壁热力系统传递函数的推导过程,墙体内外表面温度的拉氏变换存在如下关系:
式中:T(x,s)为墙体内表面温度,℃;T(a,s)为墙体外表面温度,℃;分式为墙体传递函数,其中αin为内表面对流换热系数,W/(m2·K).
结合式(5)~式(7)得出墙体内表面非稳态温度波:
式中:Ain为内表面温度振幅,℃;φn为墙体对n阶外扰的延迟时间,rad.
墙体的延迟时间φn与衰减倍数ξn为:
内表面平均温度可由传热系数计算,利用稳态传热性质,墙体内表面平均温度--Tin为:
式中:k为传热系数,W/(m2·K);Tin,air为室内空气温度,℃.
结合式(11)得出墙体内表面温度表达式:
定义内表面综合温度(Integrated temperature of inner surface,ITIS 指标),用于计算建筑外墙总传热量,同时也可以反映各朝向墙体的内表面温度综合情况.设建筑为正南北朝向:
式 中:TinE、TinS、TinW、TinN为各朝 向墙体 内表面 温度,℃;FE、FS、FW、FN为各朝向墙体的面积,m2;ΣF为墙体总面积,m2.
已知墙体内表面温度与室内空气温度,即可计算建筑墙体总传热量:
2 延迟衰减组合特性对传热峰值冷负荷的影响
2.1 建筑传热峰值冷负荷模拟计算
2.1.1 建筑模型
以长沙市某高层办公建筑为研究对象,采用 EnergyPlus 进行模拟,该建筑为正南北朝向,建筑模型如图1所示,围护结构构造与传热系数见表1.

表1 建筑围护结构参数Tab.1 Parameters of the building envelope

图1 建筑数值模型Fig.1 Building numerical model
为获得不同墙体组合,构造12 种延迟衰减特性不同的墙体,墙体结构见表2.为降低稳态传热的作用,突出延迟衰减特性的影响,结合规范[18]提出的外墙平均传热系数应小于1 W/(m2·K)的要求,各墙体传热系数均相等,数值为0.757 W/(m2·K).
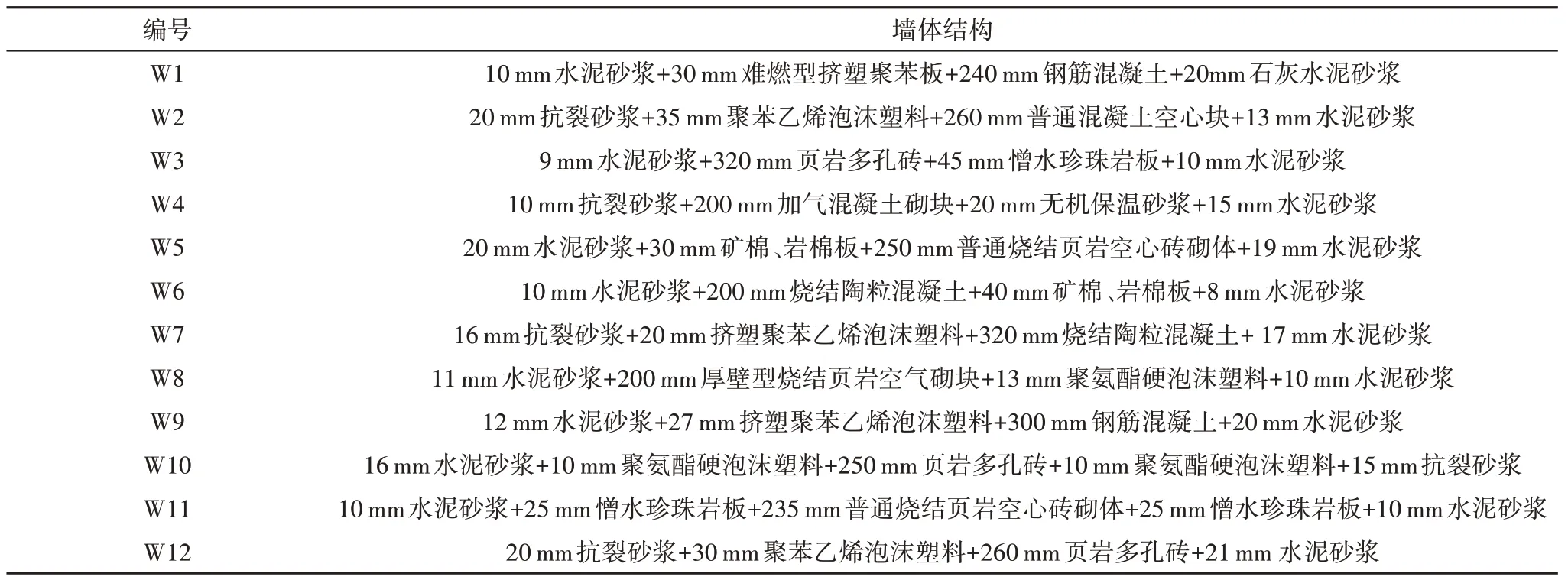
表2 W1~W12墙体结构参数Tab.2 Structural parameters of W1~W12
模拟计算中,将供冷季空调房间室内温度设为26 ℃,模拟周期设为全年,选择7 月21~22 日进行分析.
2.1.2 组合数值试验
采用正交试验设计方法研究多种墙体组合对建筑峰值传热冷负荷的影响规律,选择东(A)、南(B)、西(C)、北(D)四个朝向作为因素,W1~W12 墙体作为水平,各水平遵循随机分配原则,因素水平表见表3.
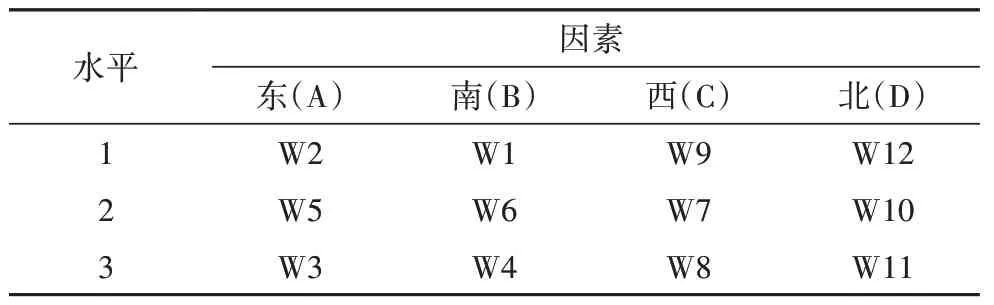
表3 因素水平表Tab.3 Factors level table
各朝向墙体内表面之间存在对流与辐射换热,常规正交试验无法满足要求,需考虑各朝向之间的交互作用.考虑西朝向与其他朝向的交互作用,选用L27(3)13正交表得到27种墙体组合,模拟得出各组建筑峰值冷负荷并作为评价指标,以此确定最优墙体组合.墙体组合情况与建筑峰值冷负荷结果如表4所示,正交试验评价指标总和见表5.

表4 墙体组合与负荷模拟结果Tab.4 Wall combination and load simulation results
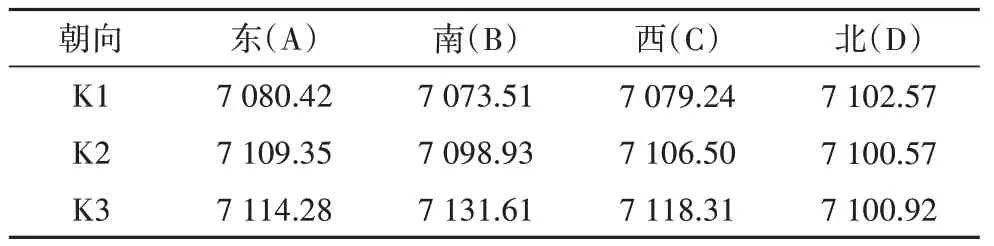
表5 正交试验评价指标总和Tab.5 Sum of orthogonal test evaluation indexes
建筑峰值冷负荷作为评价指标,其数值越小越好.如表5 所示,取各因素中评价指标总和最小的水平组成最优墙体组合,结合表3 可得出最优组合为W2、W1、W9、W10,将其设为第28 组并进行模拟,峰值冷负荷为721.57 kW,28种墙体组合模拟结果见图2.不同组合峰值冷负荷存在显著差异,第27、28组差异最大,相差11.8%.第27 组为最大值,数值为818.3 kW;第28组为最小值,数值为721.6 kW.
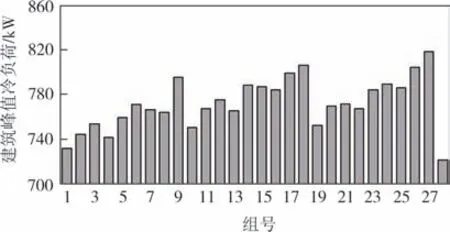
图2 建筑峰值冷负荷模拟结果Fig.2 Simulation results of building peak cooling load
2.2 墙体组合延迟衰减特性分析
2.2.1 延迟时间与衰减倍数计算
评价墙体组合延迟衰减特性,需要求出12种墙体的延迟时间与衰减倍数,计算如下:1)利用EnergyPlus模拟各墙体组合的内表面温度逐时值,温度逐时值取各楼层的平均值,再根据气象参数与式(1)、式(2)计算延迟时间与衰减倍数;2)对各组合中相同墙体的延迟时间与衰减倍数取平均值,得出最终结果.如:对表4 中墙体组合1~9 的W2 墙体的延迟时间与衰减倍数取平均值,可求出W2的延迟衰减参数.计算结果见表6.

表6 W1~W12墙体延迟时间与衰减倍数Tab.6 Time lags and decrement factors of W1~W12
2.2.2 墙体组合延迟衰减特性分析
根据表6对各组合延迟衰减特性进行分析.图3所示为各组合内表面峰值温度的出现时间,图3 中纵坐标为时间转换值,小于0的值为0:00的时刻,如-1 为23:00 等.不同组合峰值温度出现时间存在显著差异,第27 组峰值温度出现时间差异性较小,第28组差异性较大.
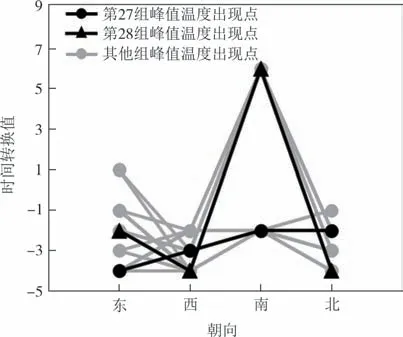
图3 各组墙体内表面峰值温度出现时间Fig.3 Walls inner surface peak temperature occurrence time of each group
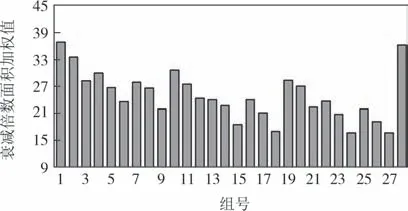
图4 墙体组合衰减倍数面积加权值Fig.4 Decrement factor area weighted value of wall combination
上述结果表明,选择不同种类的墙体进行延迟时间与衰减倍数的组合搭配,可得到建筑墙体峰值传热最小的优化墙体组合.但在实际情况下,不论从结构还是材料来说,墙体种类千变万化,即便是在地区性墙体热工性能参数的限定值下,仍然会有数量庞大的“组合方案”,导致优化墙体组合筛选的工作量巨大.为此,提出一种建筑墙体峰值传热优化组合方法,该方法无需构造大量墙体即可完成峰值传热优化设计.
3 墙体峰值传热优化组合方法
3.1 优化组合原理
墙体峰值传热优化组合方法的核心有两点:1)在合理范围内确定建筑各朝向墙体内表面峰值温度出现时间差异最大的延迟时间组(即“错峰”);2)在延迟时间与墙体热工参数等限定条件下,通过理论计算确定在当前限定条件下尽可能大的衰减倍数,进而得出最优墙体组合.为了调节延迟时间,定义错峰指标(Peak shifting indicator,PSI 指标),在PSI指标合理范围内求出墙体总传热量峰值最小的PSI组合,即可得出各朝向的最佳延迟时间.将PSI指标代入式(12),得到包含错峰指标PSIX的墙体内表面温度关系式:
式中:PSIX为各朝向的错峰指标,rad;X为朝向代码,分别表示E、S、W、N.
将式(15)代入式(13)式(14),得到墙体总传热量计算表达式.以墙体总传热量Q为目标函数,PSIX为设计变量,对该函数进行最优化求解,即可得出最优PSIX值.
3.2 案例
3.2.1 建筑墙体总传热量计算
下面进行峰值传热优化设计的案例分析.对第2节中的建筑案例进行外墙传热计算,东朝向墙体面积为1 768.5 m2,南朝向为1 660.8 m2,西朝向为 1 479.36 m2,北朝向为1 389.9 m2.外墙结构由外至内分别为:10 mm 水泥砂浆找平层+240 mm 多孔砖+15 mm难燃型挤塑聚苯板+10 mm水泥砂浆找平层,墙体传热系数为0.91 W/(m2·K),材料热工性能参数见表7,将该外墙设为基准墙体.
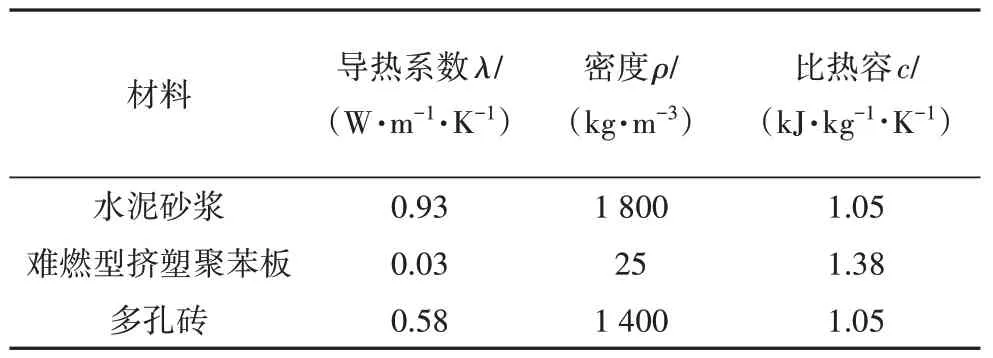
表7 墙体材料热工性能参数Tab.7 Thermal parameters of wall material
根据国家气象科学数据中心提供的长沙地区全年气象参数,选择7 月21 日的室外空气温度与太阳辐射总强度数据,由式(3)计算室外空气综合温度逐时值,对逐时值用式(4)进行拟合,得到各朝向室外空气综合温度傅氏三阶展开式,综合温度数据与拟合曲线如图5 所示.由拟合优度R2可知,曲线与数据高度吻合,表明拟合度较好.
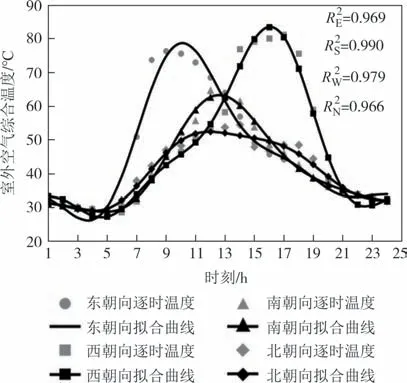
图5 逐时数据与拟合曲线Fig.5 Hourly data and fitting curve
根据式(5)~式(10)与表7 数据,使用MATLAB计算基准墙体在3 阶外扰作用下的延迟时间与衰减倍数,内外表面对流换热系数分别取8.7 与19[19],结果见表8.
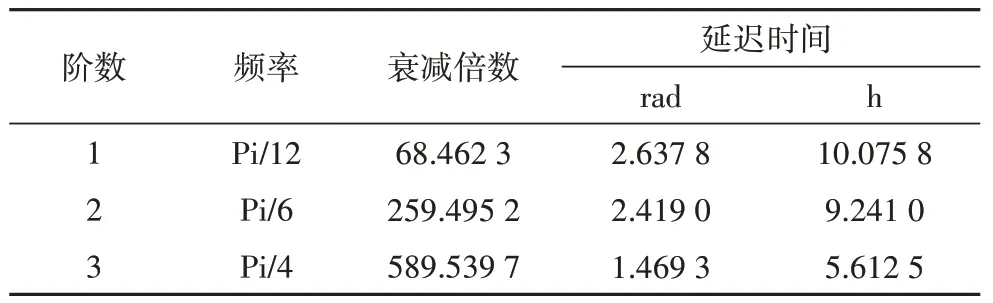
表8 墙体延迟衰减参数Tab.8 Time lags and decrement factor of wall
将表8 结果代入式(12),得出各朝向墙体的内表面温度,见式(16)~式(19).将内表面温度曲线代入式(13),求出ITIS 曲线,内表面温度曲线与ITIS 曲线如图6所示.

图6 内表面温度曲线与ITIS曲线Fig.6 Inner surface temperature curve and ITIS curve
由图6 可知,在延迟衰减作用下,墙体内表面峰值温度出现时间有所延迟,温度波幅存在衰减,但各朝向峰值温度的出现时间较为接近.将ITIS 代入式(14)计算墙体总传热量Q,室内空气温度设为26 ℃,对Q取最大值,得出墙体总传热量峰值Qmax为63.98 kW.
3.2.2 延迟时间差异性组合计算
将PSI 指标代入式(16)~式(19),得到建筑各朝向延迟时间调节式:
受限于墙体结构、材料与室外气候等因素影响,各朝向墙体的延迟时间调节需在合理范围内,即要确定PSI 指标的取值范围.选定合适的时间区间并利用弧度转换公式(时间=弧度×12/π),将时间区间转换为PSI指标区间,见表9.
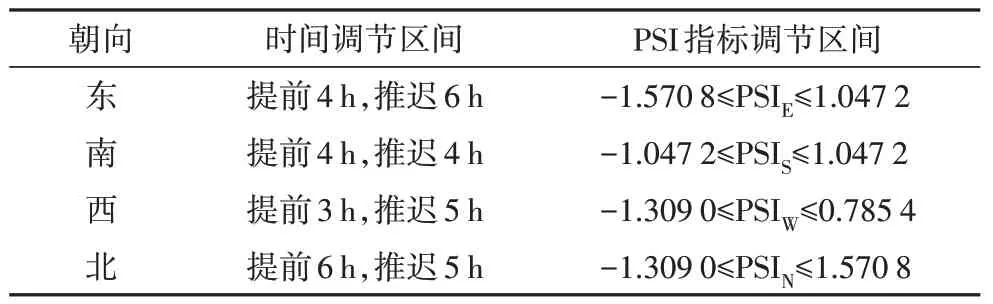
表9 PSI指标取值范围Tab.9 PSI value range
基于Visual Studio Code 平台,使用Python 语言进行编程计算,PSI 指标取值步长设为0.261 8(1 h),计算得出各朝向PSI 取值的所有组合及其总传热量峰值Qmax,Qmax最小的PSI 组合为最优解.经计算,共计得到10 692 种PSI 组合,结果见图7,其中第9 732组Qmax为最小值,数值为50.166 kW.仅考虑延迟时间的情况下,总传热量峰值相比基准墙体降低了21.5%,各朝向PSI 为:PSIE=1.047 2,PSIS=-1.047 2,PSIW=-1.309 0,PSIN=1.570 8.最佳延迟时间为:东朝向7 h,南朝向15 h,西朝向14 h,北朝向5 h.优化后各朝向内表面温度曲线见图8.

图7 不同PSI组合总传热量峰值Fig.7 Peak heat transfer of different PSI combinations
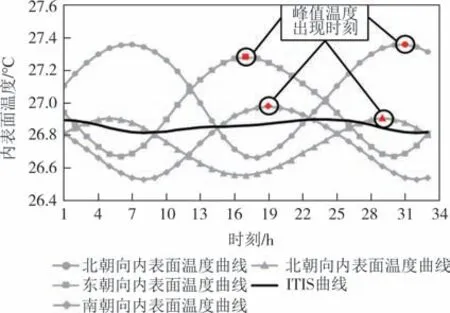
图8 优化后内表面温度曲线与ITIS曲线Fig.8 Inner surface temperature curve and ITIS curve after optimization
与图6 相比,优化后各朝向峰值温度出现时间存在显著差异,ITIS 曲线波动幅度减小.原因在于,各朝向峰值温度呈“波峰波谷”叠加态,东、北朝向温度波峰在16:00~17:00 与西、南朝向温度波谷相叠加,波峰波谷叠加可以抵消部分传热量,从而降低总传热量峰值.从表9 与最优PSI 组合的数值可以发现,东、北朝向PSI 指标为取值范围最大值,西、南朝向为最小值,说明最优PSI 数值与区间范围限值有关,区间范围的选择主要取决于目前墙体材料的热工性质.随着各种新型建筑材料的推出,若在此优化方法的基础上引入新型材料,则PSI区间范围会更大,节能率更高.
3.2.3 优化墙体计算
由文献[7]及文献[20]可知,稳定性计算法的延迟衰减结果与传递函数法一阶计算结果近似.对基准墙体分别用两种方法计算,结果见表10,两种方法的延迟衰减参数相差2.11%与3.62%,数值基本吻合.根据此结论对优化墙体进行选择,通过墙体材料的组合搭配,得出满足最佳延迟时间与基准墙体传热系数的墙体结构.使用稳定性计算法得出衰减倍数,若衰减倍数小于基准墙体,则重新组合.确定合适的墙体后,采用传递函数法计算各阶外扰的延迟衰减参数,得出内表面温度曲线与总传热量峰值.各朝向优化墙体结构与延迟衰减参数计算结果见表11.

表10 延迟衰减计算方法对比Tab.10 Comparison of time lags and decrement factor calculation methods

表11 优化墙体结构及延迟衰减参数Tab.11 Optimization of wall structure and time lags and decrement factor parameters
最终计算得出优化墙体组合的总传热量峰值为51.74 kW,相比基准墙体减少了19.1%.传热量增加的原因在于:受到传热系数与墙体结构的限制,优化墙体组合的延迟时间无法完全满足最佳PSI 组合的要求,削弱了“波峰波谷”的叠加效果.由图8 可知,虽然优化墙体组合的衰减倍数大于基准墙体,但ITIS 曲线波动区间很小,墙体衰减特性的作用被弱化.
3.3 模拟验证
为了检验墙体峰值传热优化组合方法的正确性,采用EnergyPlus 进行墙体传热量模拟.优化墙体组合与基准墙体总传热量峰值模拟结果见图9.理论与模拟计算的结果基本保持一致,数据存在偏差的原因在于理论计算仅考虑了外扰对墙体的热作用,忽略了室内环境热量对内表面的影响,该部分内容将在后续研究中展开.经模拟计算,基准墙体总传热量峰值为68.46 kW,优化墙体组合为55.58 kW,相比基准墙体降低了18.8%,与理论计算结果基本吻合,验证了该优化方法的正确.
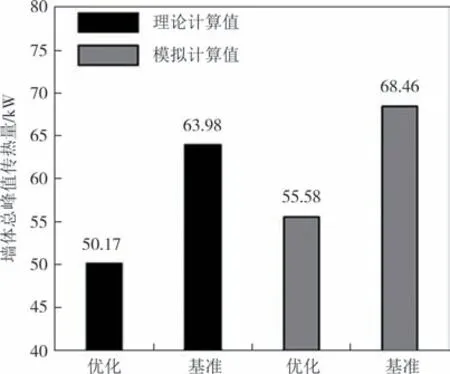
图9 理论与模拟计算对比Fig.9 Comparison between calculation and simulation calculation
4 结论
1)利用正交试验设计方法,将12 种传热系数相同、延迟衰减特性不同的墙体进行搭配,得到28 种墙体组合,采用EnergyPlus 对各组合进行建筑峰值冷负荷模拟.结果表明,各墙体组合对外扰具有明显不同的延迟衰减作用,各组峰值冷负荷存在显著差异.
2)以墙体延迟衰减特性与谐波反应法计算墙体传热为基础,提出一种外墙峰值传热优化方法,该方法在建筑不同朝向设置延迟时间与衰减倍数不同的墙体,让各朝向峰值传热量曲线呈“波峰波谷”叠加态,叠加后可降低外墙总传热量峰值.
3)通过对建筑案例进行优化分析,采用本文提出的设计方法可得到综合延迟衰减特性最佳的优化墙体组合,其总传热量峰值相比基准墙体降低了19.1%.
4)随着新型建筑材料的不断推出,墙体的延迟衰减性能范围将不断扩大,优化组合后建筑峰值传热的降低程度将更显著.
