冷弯薄壁型钢加劲腹板错列开孔柱轴压承载力研究

2023-06-03邓露蔡宇琪刘文豪刘欢

湖南大学学报(自然科学版) 2023年5期

邓露，蔡宇琪，刘文豪，刘欢

［1.湖南大学土木工程学院，湖南长沙 410082；2.工程结构损伤诊断湖南省重点实验室（湖南大学），湖南长沙 410082；3.东南大学土木工程学院，江苏南京 210096］

“双碳”背景下，国家大力推动绿色装配式钢结构建筑的发展.冷弯薄壁型钢因具有绿色节能、轻质高强、截面灵活多样等优点，被广泛应用于别墅、居民住宅以及商业建筑中［1-3］.由于冷弯薄壁型钢截面的厚度较薄，宽厚比较大，构件在压力作用下易发生屈曲破坏.为限制板件屈曲，通常在腹板或翼缘上设置加劲肋，来达到提升构件承载力的目的.常见的加劲形式有V形［4］、双V形［5］和Σ形［6］等.

为了布置水电管线，构件腹板往往需要开孔.然而，腹板开孔会造成构件截面应力分布复杂化、截面刚度降低，进而对构件的破坏模式和承载能力产生影响［7］.研究表明，开孔尺寸、孔型、开孔间距及截面的几何尺寸等对开孔试件的屈曲模式和极限承载力有一定影响［8］.姚永红等［9］研究了加劲腹板开孔卷边槽钢试件的轴压性能，发现开孔会导致试件的屈曲模式发生改变且降低试件的承载力.Wang等［10］对腹板开孔Σ 形加劲卷边槽钢试件开展了轴压试验研究，发现Σ 形加劲方式能有效地提升试件的承载效率，有助于增强孔洞周围板件变形的约束作用.张壮南等［11］对Σ 形加劲肋上开设一定数量孔的冷弯薄壁型钢柱试件进行研究.但是受到加劲肋尺寸的限制，在腹板中轴线开孔的方式并不适用于所有截面.为了便于电线、水管和燃气管等多类设施在墙体内部进行合理布置，往往在墙体立柱不同高度处开设一定数量的孔洞［12］.同时，姚永红［13］提出了在加劲肋两侧对称开孔的方案，但在同一高度开设两孔或多孔，会造成截面刚度削弱较大，进而影响试件的承载力.

为了满足管线布置对构件开孔位置的要求及降低开孔对截面刚度的削弱作用，本文提出了在腹板的不同高度处开设错列孔洞的冷弯薄壁型钢加劲腹板错列开孔柱.目前，关于腹板错列开孔冷弯型钢构件轴压性能的研究尚未见报道.此外，在《低层冷弯薄壁型钢房屋建筑技术规程》（JGJ 227—2011）［14］的设计条文中，也仅针对构件的开孔间距和开孔大小等进行了限制.本文采用经验证的ABAQUS 有限元模型，对冷弯薄壁型钢加劲腹板错列开孔柱的破坏模式和极限承载力进行了研究，讨论了开孔间距、孔型、构件长细比、腹板加劲肋板件高度和翼缘宽厚比等对极限承载力和破坏模式的影响.最后，研究发现冷弯薄壁型钢加劲腹板错列开孔柱的承载力有明显提升，为工程设计与应用提供了参考依据和数据支撑.

1 有限元模型验证

1.1 文献[13]试验概况

有限元模型选用文献［13］中的开孔V 形加劲冷弯薄壁槽钢柱试件，其材料选用Q345 级钢材.由于本文研究中涉及的对象均为开双孔的柱构件，故选取了三组文献［13］中开双孔的V 形加劲冷弯薄壁槽钢柱试件作为典型试件并进行有限元模型验证.柱试件尺寸示意图如图1 所示，详细尺寸信息见表1［13］，柱端边界条件设置为固接.试件截面厚度t取实测厚度2.98 mm，开孔尺寸ah为38.2 mm，Lh为101.6 mm.试验中加载装置选用50 t 四柱试验机.为了捕捉试件在加载过程中应变的变化状态，分别在短柱和中长柱的中间高度截面、中长柱的1/4高度截面处增设应变片.为观测试验中试件发生的畸变变形，在柱构件的中间高度截面处设置位移计.由于中长柱会发生多波失稳，在中长柱的部分翼缘和卷边交界处增设位移计.同时，在柱试件的加载端布置轴向位移计.试验时，采用逐级加载的加载方案，每级加载10 kN，直到加载至预估极限承载力的70%左右，每级加载量减小到1～2 kN，直至达到峰值荷载.

表1 试件的实测尺寸参数［13］Tab.1 Measured dimensions of the test specimens［13］

图1 试件尺寸及符号定义［13］Fig.1 Test specimen dimension and symbol definition［13］

1.2 模型建立

本文通过与文献［13］中的试验结果对比来验证有限元模型的准确性.采用ABAQUS 有限元软件建立冷弯薄壁型钢加劲腹板开孔柱有限元模型.模型均选用S4R 单元模拟.为了与文献试件编号统一及便于比较，验证模型的编号与文献［13］中试验试件的编号一致.因文献［13］中试件两端的边界条件均为固接，故在有限元模型中约束顶端和底端除加载方向之外的其他所有自由度，并在顶端截面形心处施加位移荷载.构件网格尺寸取10 mm.因孔洞附近易发生应力集中现象，故对孔洞周围网格进行局部加密处理，孔边网格尺寸为5 mm.有限元模型的边界条件和网格划分情况如图2所示.

图2 边界条件和网格划分Fig.2 Boundary conditions and meshing

材料选用Q345 钢，为了有效避免有限元分析后期收敛困难，减少计算分析试件，钢材本构关系采用双线性强化模型.弹性模量E=206 GPa，第二模量Eε=E/50，泊松比为0.3，屈服强度fy=363.0 MPa，极限强度fu=508.7 MPa［13］.构件因冷弯效应提高的屈服强度能近似抵消薄膜残余应力对冷弯型钢构件力学性能的不利影响［15-16］.故在有限元模型建立中，未考虑冷弯效应和残余应力对构件受力性能的影响.

由于试件在制作和运输等过程中会产生初始缺陷，且初始缺陷会对试件的力学性能产生不可忽略的影响，因此有必要在有限元分析过程中引入初始缺陷［17］.在有限元建模的过程中，首先，进行特征值屈曲分析，提取一阶屈曲模态，所得一阶屈曲模态均发生以畸变屈曲为主的屈曲失效模式；其次，通过修改INP 文件中的关键词在一阶屈曲模态基础上引入初始缺陷，畸变屈曲几何缺陷取0.94t［18］；最后，利用通用静力分析方法［19］进行有限元分析，以获取构件的破坏模式、荷载-位移曲线和极限承载力.

1.3 模型验证

采用上述建模方法建立的有限元模型对文献［13］中的3 个试件进行计算分析，并与试验结果进行对比.

有限元分析中，构件均发生以畸变屈曲为主的破坏模式，与文献［13］中试件的破坏模式基本一致，有限元分析与试验各自所得的破坏模式对比如图3所示.试验和有限元分析中，构件翼缘的最大变形均发生在构件的1/2 高度位置处.同时，翼缘绕翼缘与腹板间的交线发生一定程度的向外转动，孔洞两侧的翼缘变形尤为明显.为了验证模型的荷载-位移曲线，与文献［13］中的试验结果进行了对比，如图4 所示.由图4 可知：有限元分析得出的荷载-位移曲线与通过试验得出的结果吻合较好.通过比较试验和有限元分析获得的极限承载力，发现二者基本保持一致.由表2可知，试验获得的极限承载力Fu，Test与有限元分析获得的极限承载力Fu，FEM之比的均值和变异系数分别为0.99、0.061.有限元计算值与试验结果误差均在10%以内，这主要是由于在有限元分析中将柱端约束考虑为理想条件，使其与试验过程中可能存在的对中误差下的实际约束条件存在一定差别.综上，该有限元模型可以较准确地模拟冷弯薄壁型钢加劲腹板开孔轴压柱的破坏模式、荷载-位移曲线和极限承载力，验证了有限元建模的准确性.

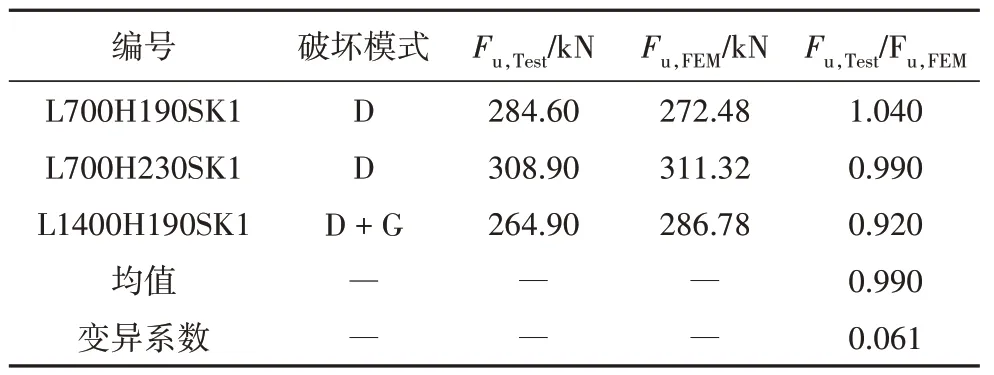
表2 试验结果与有限元结果比较Tab.2 Comparison of test and FEM results

图3 破坏模式验证Fig.3 Validation of failure modes

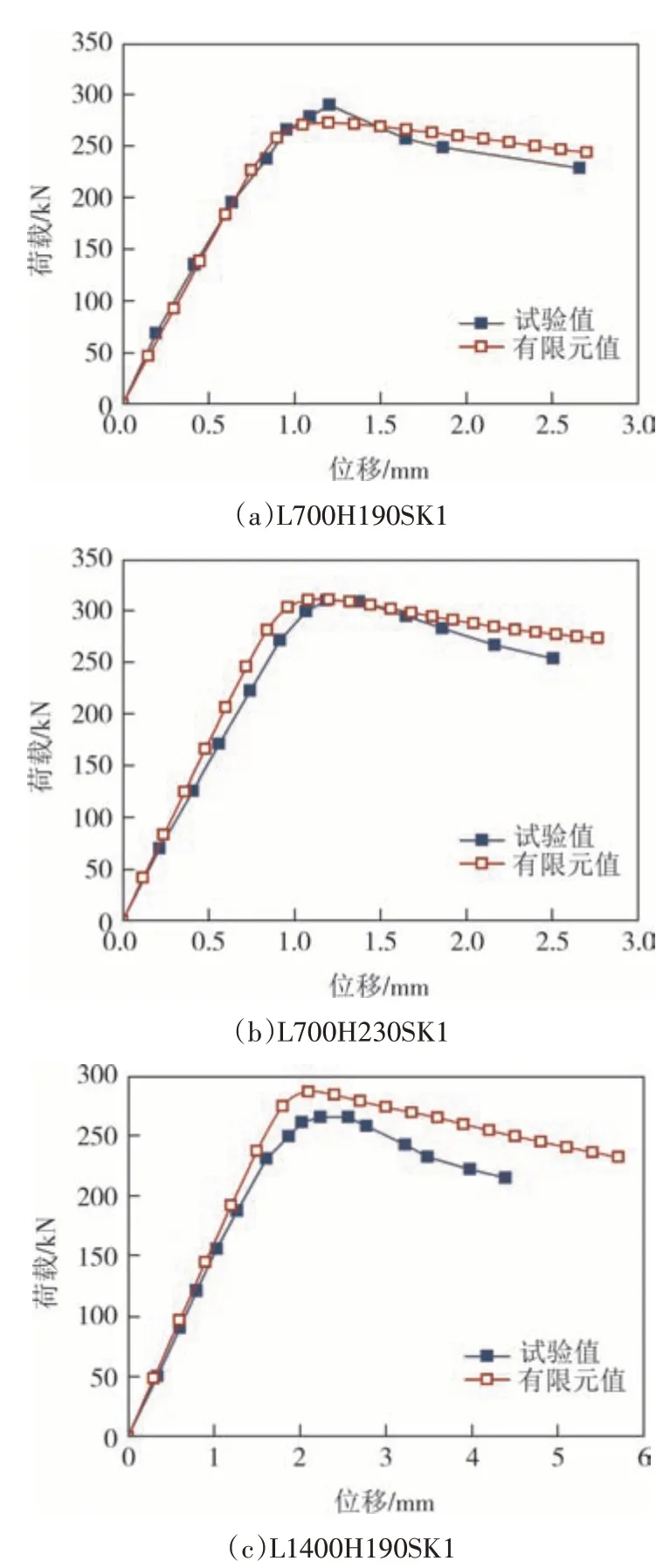
图4 荷载-位移曲线验证Fig.4 Validation of load-displacement curves

2 模型参数及计算结果

2.1 模型参数

按照第1 节方法建立加劲腹板错列开孔柱有限元模型.根据《冷弯薄壁型钢结构技术规范》（GB 50018—2002）［20］中关于材料属性的规定，Q345 钢的弹性模量取206 GPa，第二模量ES=E/100，屈服强度fy取标准值345 MPa，抗拉强度fu为448 MPa［21］，泊松比取0.3.本文共设计了177 个冷弯薄壁型钢加劲腹板错列开孔轴压柱，研究开孔间距、孔型、构件长细比、腹板加劲肋板件高度、翼缘宽厚比对冷弯薄壁型钢加劲腹板错列开孔轴压柱受力性能的影响.截面形状和开孔位置示意图见图5.截面壁厚t为1.5 mm、2.0 mm、2.5 mm、3.0 mm，截面高度H为190 mm、230 mm，截面翼缘宽度B为60 mm、75 mm、90 mm，加劲肋深度S1为15 mm，加劲肋和腹板的夹角为135°，卷边D长度为20 mm.开孔间距d取0～1 400 mm.孔型分别为椭圆孔（O）、矩形孔（R）、圆孔（C）和菱形孔（L）.短柱构件长度取700 mm，中长柱构件长度取1 000 mm 和 1 400 mm，长柱构件长度取2 100 mm.腹板加劲肋板件高度h分别为0 mm（等同于布置V 形加劲）、20 mm、30 mm 和40 mm.本文构件参数变量设置如表3所示.椭圆孔和矩形孔的开孔高度ah为38 mm，开孔宽度Lh为100 mm；圆孔的直径为38 mm；菱形孔的开孔高度和宽度均为38 mm.

表3 构件参数变量设置Tab.3 Parameter variables of typical specimens

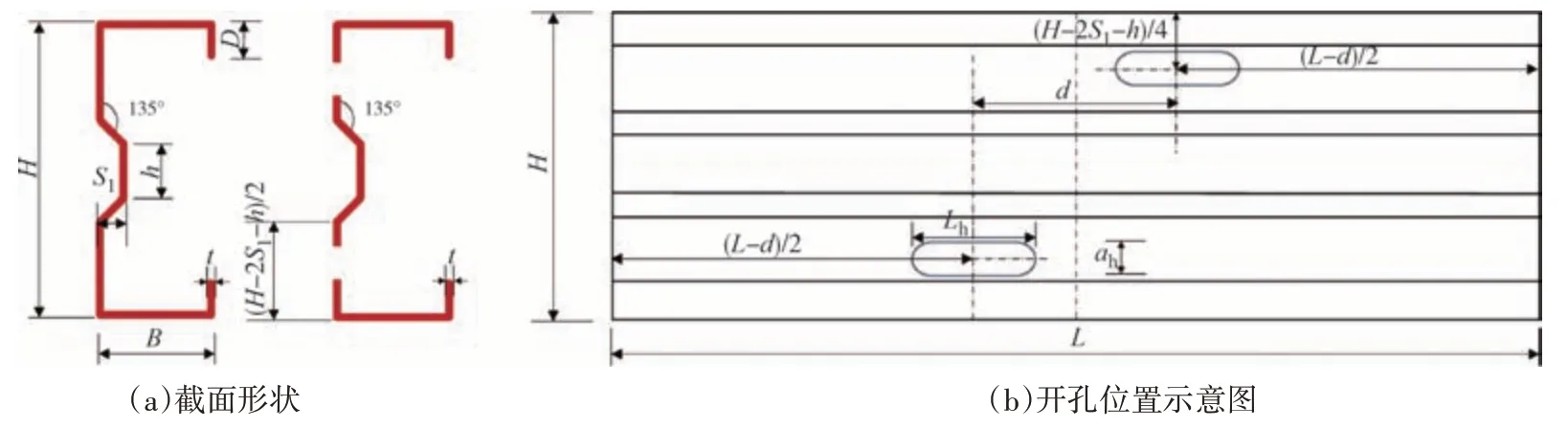
图5 构件尺寸及符号定义Fig.5 Specimen dimension and symbol definition

构件编号中的各字母及数字的命名规则如下：L700H190B60h0-C2-0 代表柱长L为700 mm，截面腹板高度H为190 mm，构件截面翼缘宽度B为 60 mm，腹板加劲肋板件高度h为0 mm，孔型为圆孔（C），开孔总个数为2 个且开孔间距为0 mm（即并排）的构件.

2.2 破坏模式及应力分布

根据ABAQUS 有限元模拟结果，本文中构件主要发生以畸变屈曲为主的屈曲失效破坏，如图6 所示.当柱长为700 mm 时，构件发生翼缘与卷边的畸变屈曲，伴有孔边板件的局部鼓曲.当开孔间距为200 mm 时，构件发生呈中心对称的I-I 型（翼缘内收）畸变屈曲，如图6（a）所示.构件的最大畸变变形发生在构件中间高度位置.当柱长为1 000 mm 和1 400 mm 时，构件主要发生畸变屈曲，如图6（b）和（c）所示.当柱长为2 100 mm 时，构件呈现以畸变屈曲为主的屈曲失效模式，伴有绕弱轴的整体弯曲和开孔板件周边的局部鼓曲，如图6（d）所示.随着错列开孔间距的增大，畸变屈曲的模式也由I-I 型（翼缘外张）转变为O-O 型.可见孔洞的存在改变了中长柱的屈曲形态.

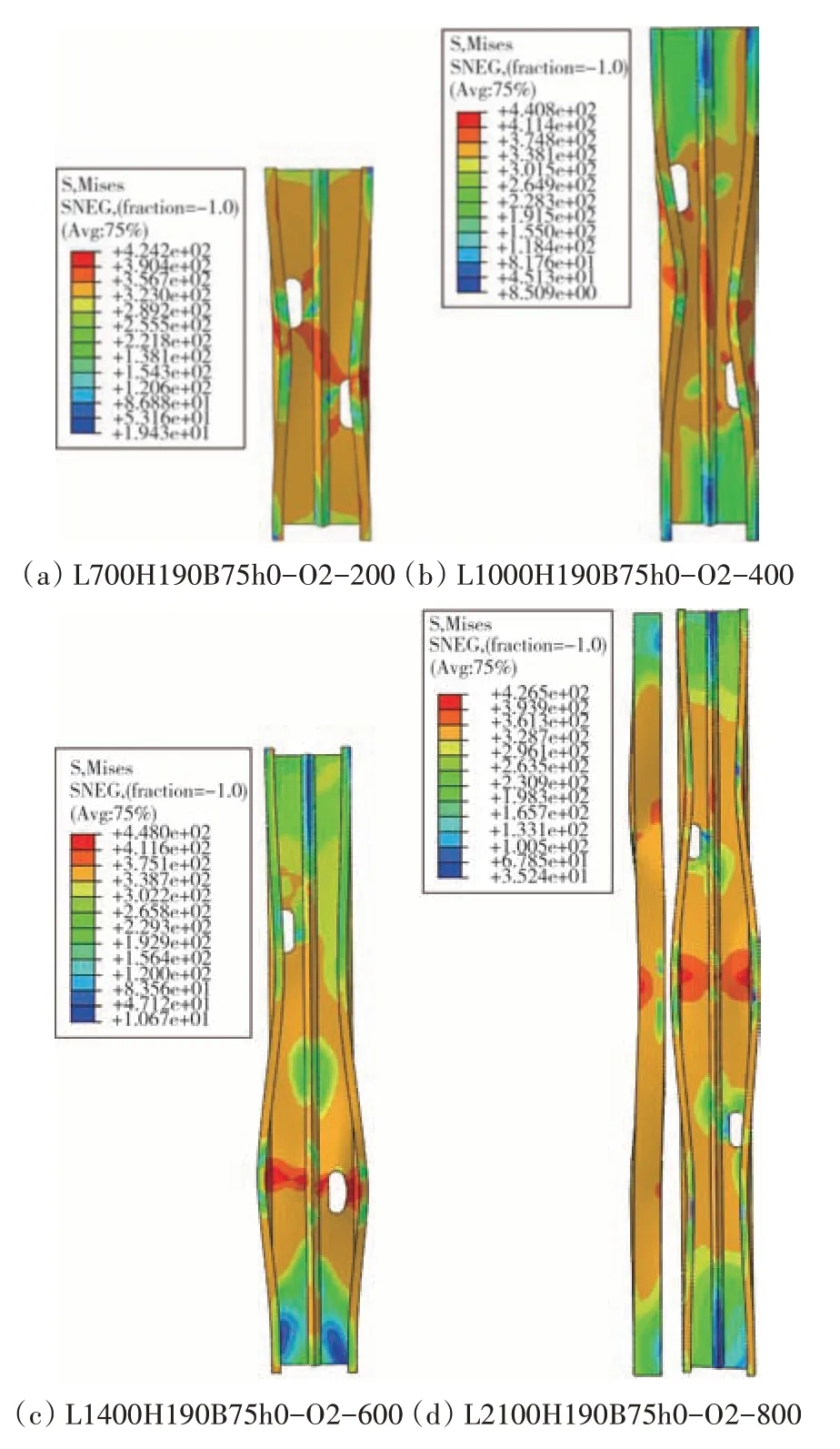
图6 错列开孔柱屈曲失效模式Fig.6 Buckling modes of members with staggered holes

图7（a）和7（b）表明，当孔型为圆孔时，最大变形出现在构件的上半部分，即靠近顶端的开孔处；当孔型为菱形孔时，最大变形出现在构件的下半部分，即靠近底端的开孔处.当孔型为椭圆孔和矩形孔时，构件出现了上述类似的差异现象.孔型对构件屈曲失效时的变形有一定影响.由图7 还可知，当孔型为菱形孔和矩形孔时，在开孔尖角处易发生应力集中.故当孔型不同时，由于几何形状的差异性，开圆孔和椭圆孔的构件比带有尖角的菱形孔和矩形孔的试件表现得更为优越.

图7 不同孔型的柱屈曲失效模式Fig.7 Buckling modes of members with different hole shapes

2.3 荷载-位移曲线

为了直观地反映构件的刚度和极限承载力的变化，图8 给出了L700H190h0-O2和L1400H190h0-O2系列构件在轴压作用下的荷载-位移曲线（图中B60-0表示为翼缘宽度为60 mm，错列开孔的开孔间距为0 mm）.从图8 中可以看出荷载-位移曲线受开孔间距、翼缘宽厚比影响较大.荷载-位移曲线均呈现出直线上升、曲线上升和下降三个阶段，即弹性、弹塑性和破坏三个阶段.当开孔间距和翼缘宽厚比较大时，荷载-位移曲线直线段较陡，变形能力较弱，弹性工作阶段较长.当达到极限荷载的80%时，进入弹塑性工作阶段，承载力相对较强.由图8（a）可知，各构件的荷载-位移曲线变化趋势大体一致.在加载的初始阶段，荷载随着位移的增大而呈线性增加，表明构件在加载阶段处于弹性受力阶段；当荷载达到峰值时，由于构件出现局部屈曲从而增长得较为缓慢，曲线趋于平缓.当翼缘宽度增加时，荷载-位移曲线直线段斜率随之增加，说明构件刚度随翼缘宽度的增加而增大.同时，临界荷载对应的位移也随之后移.图8（b）的变化规律与图8（a）基本一致.

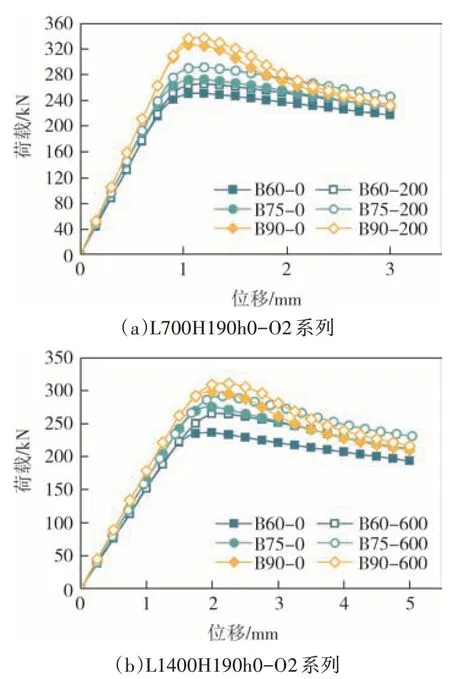
图8 荷载-位移曲线图Fig.8 Load-displacement curves

3 有限元参数分析

3.1 开孔间距的影响

图9 给出了加劲腹板错列开孔柱构件的极限承载力随开孔间距变化曲线图.当柱长为700 mm 时，构件的极限承载力随着开孔间距的增大而先慢后快地增加.当开孔间距从0 mm 增加到200 mm 时，构件的极限承载力的上升幅度约为10%；当柱长为1 000 mm时，构件的极限承载力与错列开孔的间距近似呈线性正相关，极限承载力平均增长了约16.2%；当柱长为1 400 mm 时，构件的极限承载力随着错列开孔的间距增加几乎呈线性增长的趋势.出现该规律的可能原因是构件腹板开孔引起了腹板局部应力重分布，随着双孔之间开孔间距的增大，双孔的相互影响降低，双孔对腹板受力性能的削弱降低，此时轴压柱构件的承载力得到提升.因此，增加开孔间距对轴压柱构件的稳定承载力有一定提升作用.

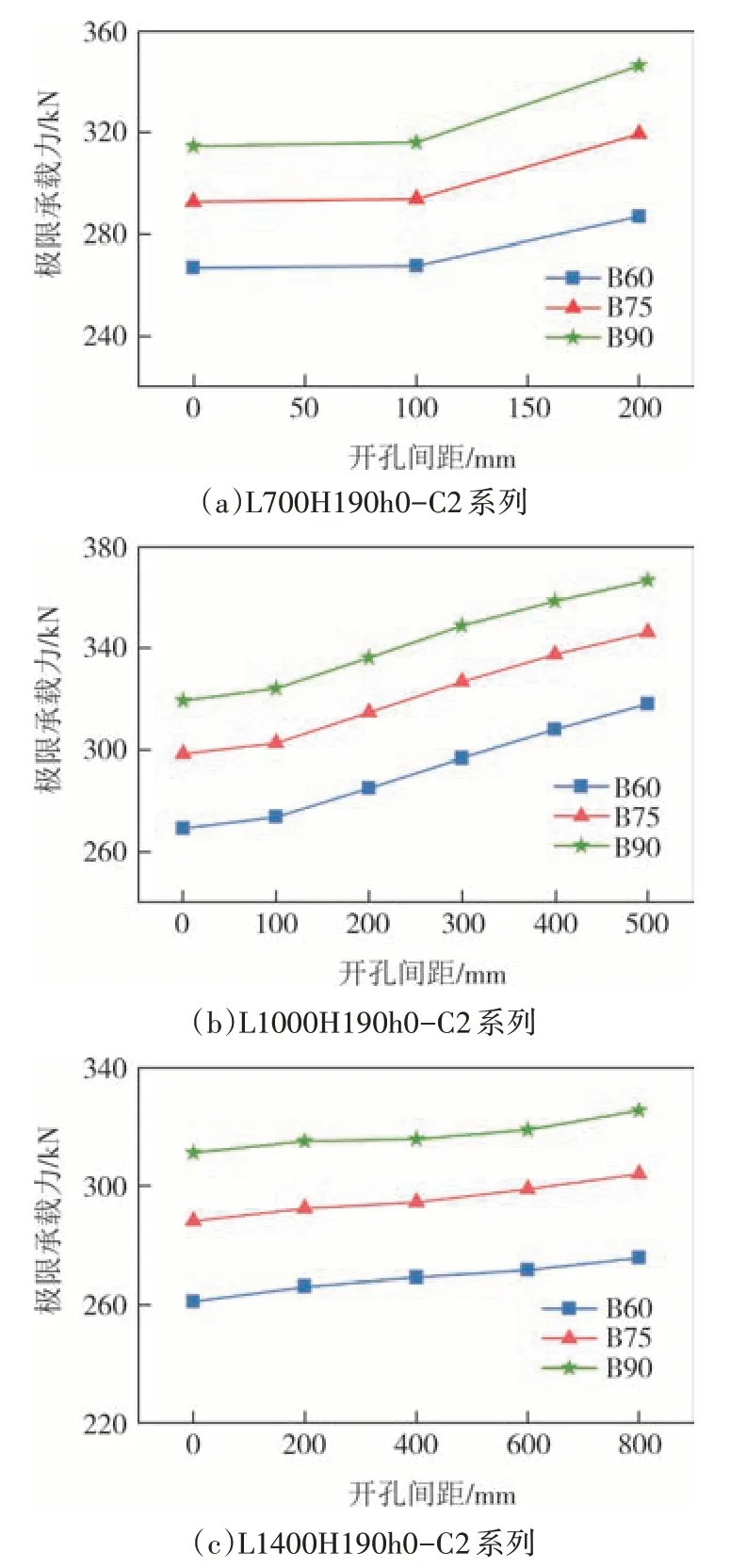
图9 不同开孔间距的柱构件承载力对比Fig.9 Comparison of bearing capacities of members with different hole spacings

3.2 孔型的影响

总体上，当孔型不同，孔洞的宽度和高度分别相同时，开椭圆孔构件的极限承载力都要略高于开矩形孔的构件，开菱形孔构件的极限承载力都要略高于开圆孔的构件，如图10所示.对于柱长为1 000 mm的构件，当开孔间距提升至600 mm 时，开椭圆孔的构件极限承载力提升了28.6%，开矩形孔的构件极限承载力提升了29.4%，开圆孔的构件极限承载力提升了20.7%，开菱形孔的构件极限承载力提升了19.2%.在开孔宽度和开孔高度相同的情况下，开椭圆孔、菱形孔的构件极限承载力高于开矩形孔、圆孔的构件.出现上述现象可能是由于在开孔宽度和开孔高度相同的情况下，矩形孔和圆孔的开孔面积大于椭圆孔和菱形孔［22-23］，因此对截面的削弱更大.这也说明孔型对构件的受力性能有一定影响.

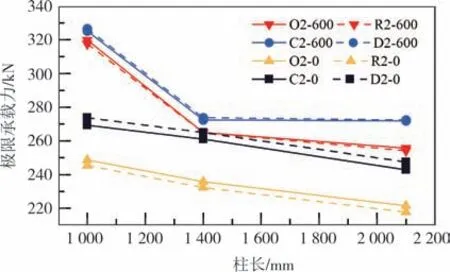
图10 不同孔型的柱构件承载力对比（H190B60h0系列）Fig.10 Comparison of bearing capacities of members with different hole shapes for series H190B60h0

3.3 构件长细比的影响

通过改变构件的柱长，其他截面参数保持不变，计算各构件模型的极限承载力结果如表4 所示.在截面尺寸相同时，错列分布的孔洞对极限承载力的影响随着长细比的增加逐渐降低，如图11 所示.因构件的边界条件为固支，故计算长度l0=μl中修正系数μ取0.5.本文中构件截面为单轴对称开口截面，按照《冷弯薄壁型钢结构技术规范》（GB 50018—2002）［20］计算构件的长细比最大值均为绕弱轴的长细比.

表4 不同长细比柱构件的极限承载力Tab.4 Bearing capacities of members with different slenderness ratios

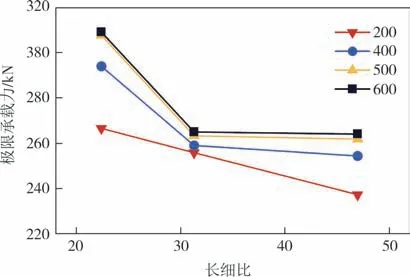
图11 不同长细比的柱构件承载力对比（H190B60h0-O2-*系列）Fig.11 Comparison of bearing capacities of members with different slenderness ratios for series H190B60h0-O2-*

由图11 可知，当构件的开孔间距为200 mm、400 mm、500 mm、600 mm时，极限承载力曲线的变化规律趋于一致，呈极限承载力随长细比的增大而减小的变化趋势.当柱构件的长细比从22.4 增长到31.3 时，承载力降低最明显.随着长细比的增大，柱构件的破坏模式发生了改变.从表4 可知，当柱构件的长细比为31.3时，构件发生畸变屈曲.当长细比增加到47.0 时，构件发生畸变屈曲的同时伴随绕弱轴的整体屈曲，极限承载力随之下降.总之，随着构件的柱长增加，构件长细比增大，构件极限承载力呈下降的趋势.

3.4 腹板加劲肋板件高度的影响

图12 给出了L1400H230-O2-800 和L2100H23 0-O2-800 系列构件的极限承载力与腹板加劲肋板件高度的变化关系.随着腹板加劲肋板件高度的增加，构件的极限承载力提升.当加劲肋宽度S1保持不变，腹板加劲肋板件高度h=20 mm 时Σ 形加劲截面构件的极限承载力比V 形加劲截面构件提升约6.5%.

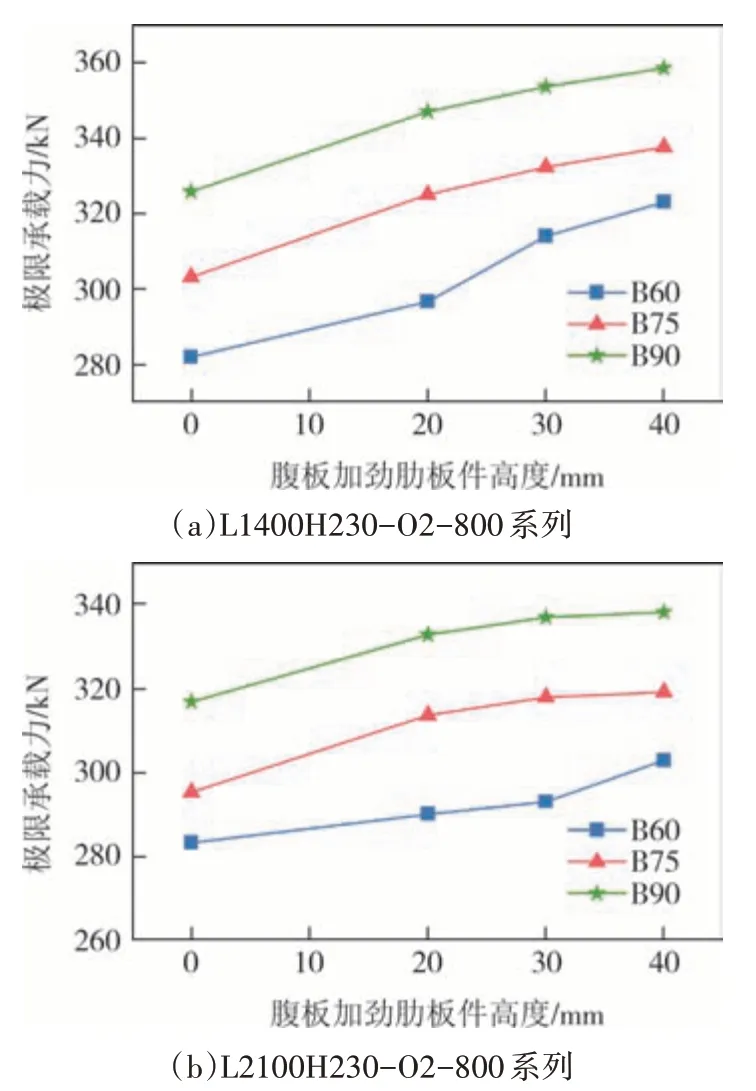
图12 腹板加劲肋板件高度变化时的柱构件承载力对比Fig.12 Comparison of bearing capacities of members with different heights of web-stiffeners

3.5 翼缘宽厚比的影响

保持其他条件不变，改变截面厚度，当翼缘宽度保持为90 mm 时，厚度分别为1.5 mm、2.0 mm、2.5 mm、3.0 mm，对应的翼缘宽厚比分别为60、45、36、30.图13 给出了构件的极限承载力随翼缘宽厚比的变化情况，构件的极限承载力随翼缘宽厚比增大而减小.当柱长为1 400 mm 和2 100 mm 时，极限承载力曲线变化趋势一致.当柱长为1 400 mm，翼缘宽厚比从30 增至60 时，柱构件的极限承载力降低60.0%.当柱长为2 100 mm，翼缘宽厚比从30增至60时，柱构件的极限承载力降低65.3%.这是因为在保持翼缘宽度条件下，随着截面厚度的增加，翼缘宽厚比减小，翼缘对腹板的支承作用加大，从而提升了构件的极限承载力.

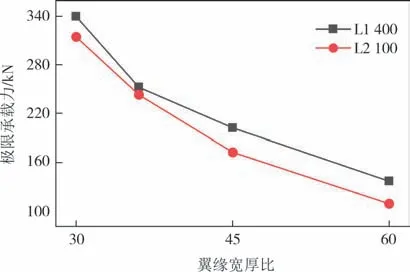
图13 翼缘宽厚比变化时的柱构件承载力对比（H230B90h0-O2-600系列）Fig.13 Comparison of bearing capacities of members with different flange width-thickness ratios for series H230B90h0-O2-600