复合加固方形木柱的恢复力模型
2023-06-03周长东闫佳玲阿斯哈
周长东,闫佳玲,阿斯哈
[1.北京交通大学 土木建筑工程学院,北京 100044;2.结构风工程与城市风环境北京市重点实验室(北京交通大学),北京 100044;3.北京首都开发控股(集团)有限公司,北京 100101]
木结构是中国古建筑的主要形式,木柱是木结构的主要支承构件.为了提升古建木结构的力学性能,保证其使用安全性,需要对腐朽、老化和损伤的木柱进行加固.外包纤维(Fiber Reinforced Polymer,FRP)布是木结构加固的有效方法[1-5],试验结果[6-7]表明,采用碳纤维(Carbon Fiber Reinforced Polymer,CFRP)布加固能够显著增强木结构的抗震性能,大幅提升木结构的安全性.CFRP布加固木柱能够有效约束和限制木柱的横向膨胀和变形,从而提高木柱受压承载力和延性,改善木柱的抗震性能,但仅采用外包纤维布的抗震加固效果有限.而在木材表面开槽,然后用植筋胶将筋材内嵌到槽中加固木构件的效果已经被加固木梁的试验研究所证实[8-12],内嵌筋材可以有效提高木梁的抗弯承载力.相关研究[13]表明,内嵌钢筋能够提升木柱的抗压强度,但也存在内嵌筋材易与木槽剥离、筋材外露等问题.
综合外包FRP 布和内嵌筋材加固法,本文提出采用内嵌钢筋外包CFRP布复合加固方形木柱,加固柱的侧向承载力和抗震指标均有明显提高.为了分析复合加固木柱和加固后木结构的抗震性能,需要建立复合加固木柱的恢复力模型.目前针对钢筋混凝土柱[14]、钢柱等其他材料柱的恢复力模型研究较多,也有学者基于试验建立了木构架[15]、CFRP 布加固木构架[16-17]以及斗栱与榫卯节点[18]的恢复力模型,但尚未发现针对木柱和加固木柱恢复力模型的研究.因此本文基于8 根方形木柱的低周往复荷载开展试验研究和理论分析,建立了复合加固方形木柱的抗弯承载力计算公式,提出了复合加固方形木柱的恢复力模型,为复合加固木柱的地震响应分析和实际工程应用提供了参考依据.
1 试验概况
1.1 试件设计
方形木柱采用图1 所示的试验装置进行试验,柱脚放入套箍式钢底座中,通过拧紧水平向螺栓固定木柱,然后通过2 个锚杆将钢制底座锚固在固定基础上;固定基础两端采用机械千斤顶进行支顶,防止其在试验过程中滑动.以某单层古建木结构柱为原型,采用1∶3.6 的缩尺比例设计了试验试件的尺寸.从嵌固底座顶部到水平作动器中心线的距离为 1 800 mm,试验段尺寸为270 mm×270 mm×1 800 mm.试件整体高度为2 600 mm,其中包含试验段高度 1 800 mm,底部固结支座的高度450 mm,以及水平加载点到柱顶距离350 mm.8 根试件的具体加固方案如图2所示.
1.2 材料性能
试验用木材为红松,各项物理力学参数均通过木材的无瑕疵小试样测试确定,具体见于表1.材性试验木材与试验木柱源于同一批木材.内嵌钢筋等级为HRB400,通过对拉试验得到的材料性能参数列于表2.表3中CFRP布的材料性能参数由生产厂家提供.

表1 木材材料性能Tab.1 Material properties of timber

表2 钢筋力学性能Tab.2 Mechanical properties of steel bars

表3 CFRP布材料性能Tab.3 Material properties of CFRP strips
1.3 试验方法
采用图1 所示的拟静力试验方法加载.首先通过试件顶部的千斤顶施加竖向荷载.根据原型木柱的轴压比0.016和试验用木材的顺纹抗压强度,可以计算确定竖向荷载的大小为43 kN.之后通过作动器施加水平荷载.柱端水平低周反复荷载采用位移控制,当控制位移为1.125 mm、2.25 mm、4.5 mm、6.75 mm和9 mm 时每级循环1 次,从18 mm 控制位移开始取位移级差为18 mm,每级循环3 次;水平荷载下降至承载力的85%时,试验结束.
1.4 试验现象
各试件的试验现象和破坏形态较为相近.随着水平循环加载进程,产生木材纤维的撕裂声,响声不断增大,且逐渐连续.当达到一定的水平位移后,试件发生木材纤维的受拉断裂破坏,如图3 所示.破坏时木柱水平承载力骤降,脆性特征显著.对比试件在90 mm时,水平承载力达到峰值,加载至126 mm时达到试件的极限位移.仅嵌筋试件的峰值承载力产生于108 mm 的加载循环,极限位移则位于144 mm 的加载循环.试件TC-S-4 在加载至水平位移144 mm时,达到峰值荷载,且在162 mm 的加载循环中,水平荷载下降至峰值的85%.试件TC-S-5 的峰值荷载出现于108 mm 的加载循环,水平加载位移144 mm 时发生脆性破坏,在162 mm 的加载循环中达到极限位移.试件TC-S-7在水平位移达到144 mm时,达到峰值荷载,其极限位移位于180 mm 的加载循环.综上所述,复合加固方法不能够改变木柱的破坏形态,但可以延缓其破坏发生的进程,改善破坏的程度.
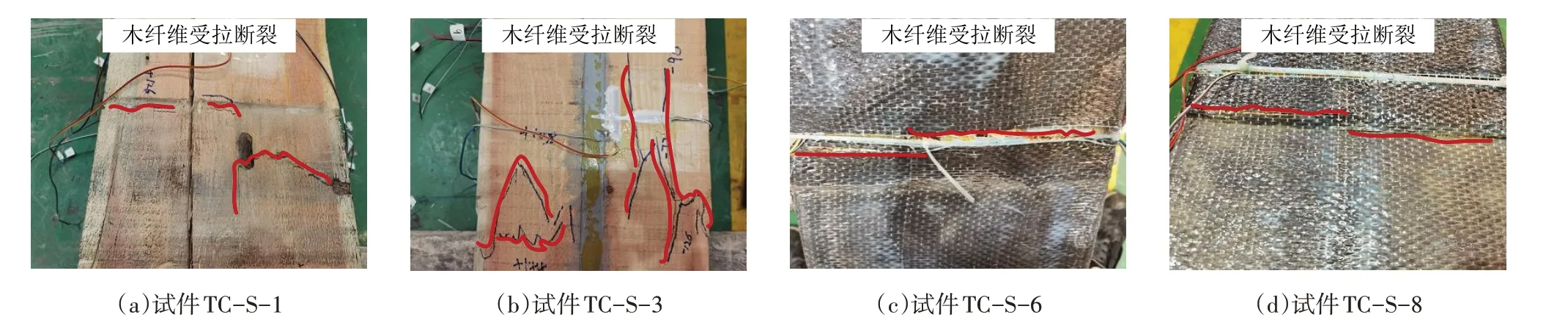
图3 试件破坏形态Fig.3 Failure modes of specimens
1.5 滞回曲线
木柱的滞回曲线如图4 所示,未加固木柱的滞回曲线捏拢现象明显且滞回环面积较小,耗能性能较差.嵌筋加固试件随着配筋率的增加极限位移增加、滞回环面积增大,耗能能力增强;由于无法限制裂缝的发展,滞回曲线捏拢现象依旧明显.全包CFRP 布试件的延性有所提高,侧向承载力增大且承载力下降缓慢,滞回曲线的捏拢现象得到很好的改善.相比于内嵌钢筋或外包CFRP 布单项加固试件,内嵌钢筋外包CFRP 布复合加固试件的整体性能明显提升,侧向承载力增大的同时限制了裂缝的发展,改善了捏拢现象;滞回环更加饱满,承载力下降更加缓慢,试件整体耗能性能更优.
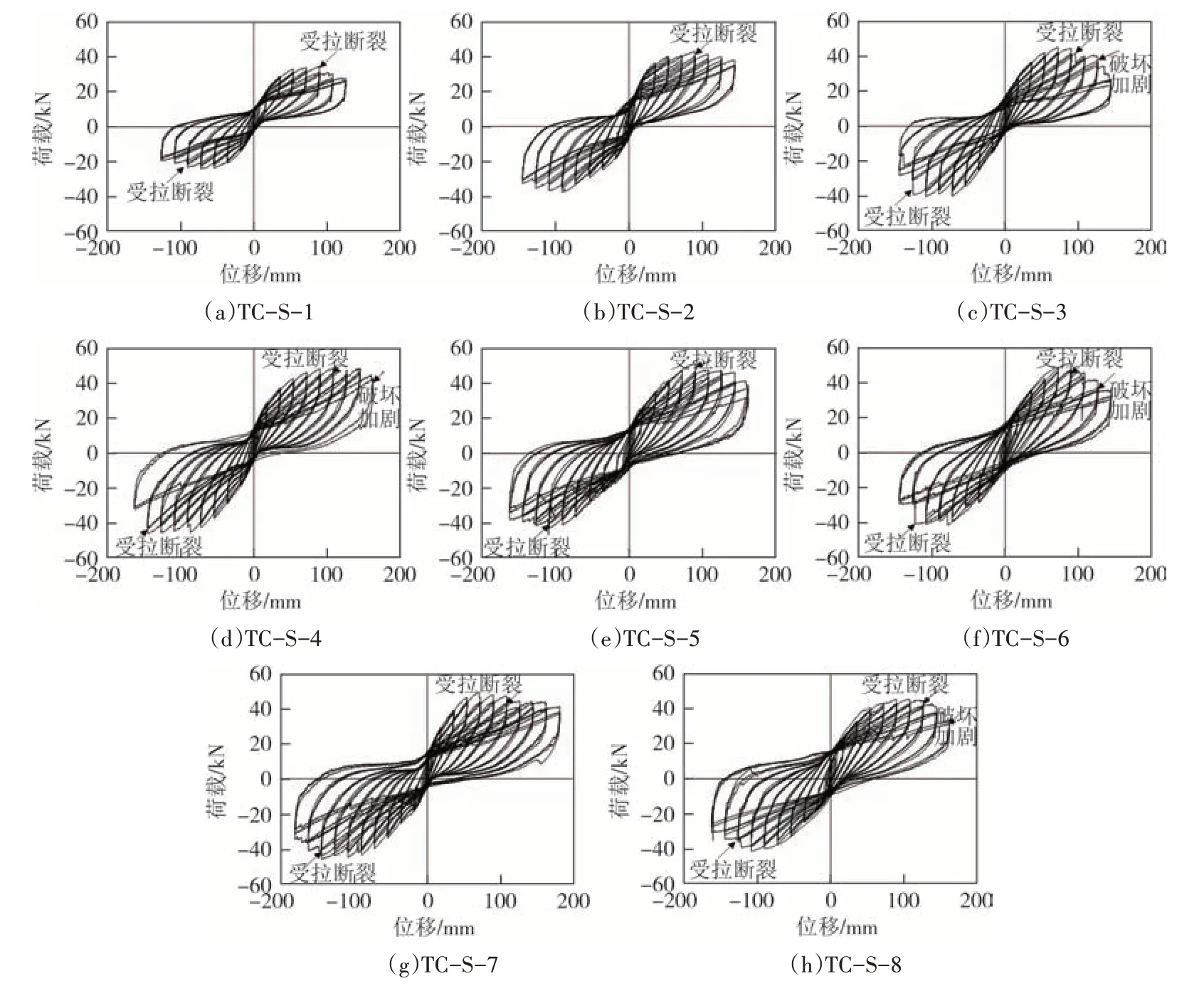
图4 试件滞回曲线Fig.4 Hysteretic curves of specimens
1.6 主要试验结果
主要试验结果见表4,其中Pmax为峰值荷载;Δmax为峰值荷载点对应的位移;Py为屈服荷载;Δy为屈服荷载点对应的屈服位移;Δu为荷载下降至峰值荷载85%时的极限位移.屈服点采用等效能量法确定.与试件TC-S-1相比,试件TC-S-2和TC-S-3侧向承载力分别提升了37.80%和46.09%;随着配筋率的提高,试件的侧向承载力增加.相比于未加固柱,各加固试件的侧向承载力和变形能力都有了不同程度的提高,复合加固效果更佳;试件TC-S-8 破坏部位木节等初始缺陷较多,导致其承载力没有明显提升.
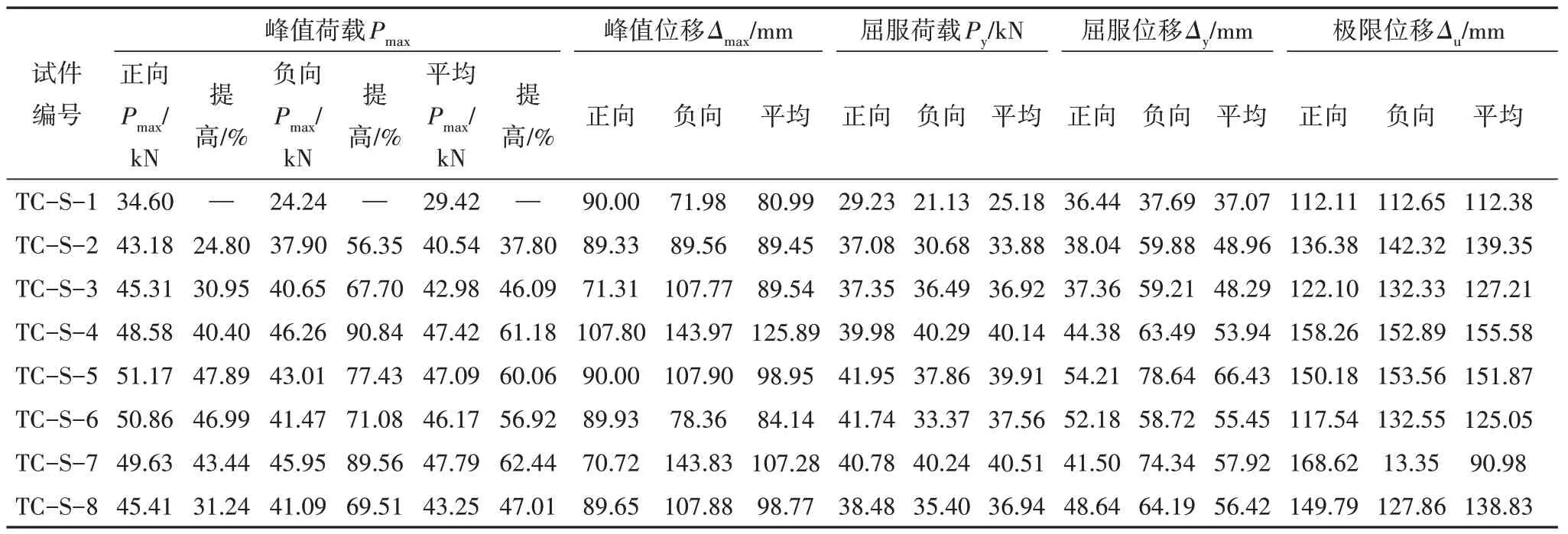
表4 主要试验结果Tab.4 Main test results
2 CFRP布约束方形木柱计算模型
2.1 CFRP布约束方形木柱抗压强度
采用CFRP布环向加固木柱,可以约束木柱在顺纹受压时产生的横向膨胀,从而提高木柱的顺纹抗压强度和变形能力.本文参照Lam 和Teng[19]提出的FRP 约束混凝土矩形柱的强度计算模型,根据课题组相关研究[20],确定CFRP约束方形木柱抗压强度计算公式为:
式中:fcc为CFRP布约束后方形木柱顺纹抗压强度;fco为未约束方形木柱顺纹抗压强度;1.6 为约束有效性系数;fl为CFRP 布的有效约束应力;fh为未约束方形木柱的横纹径向抗压强度.
2.2 CFRP布的侧向约束力
CFRP 约束矩形柱的有效约束区域如图5 所示,其中b和h分别为矩形柱截面的宽度和高度.从图5中可看出约束在角部及核心内部的作用最强,边长中部较弱,即存在不均匀的现象.许多学者[21-22]将矩形截面等效为圆形截面来综合考虑截面尺寸及CFRP 布强度、弹性模量和加固量的影响.需要说明的是,考虑到目前缺乏FRP 约束矩形木柱的理论研究,因此本文沿用FRP 约束混凝土柱的既有理论进行分析和计算.文献[22]将等效圆柱直径D定义为截面的对角线长度,即.本文试件为方形截面,即b=h,则
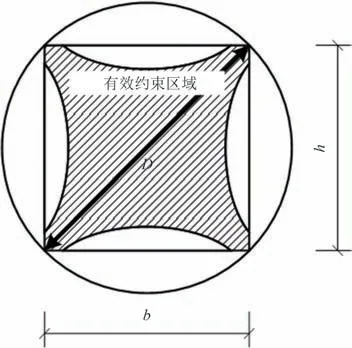
图5 矩形柱的有效约束区域Fig.5 Effective confinement area of the rectangular column
当矩形柱外包CFRP布时,根据其等效圆柱模型进行受力分析,如图6 所示.设等效直径为D;CFRP布的宽度为bfrp,厚度为tfrp,环向拉应力为ffrp,弹性模量为Efrp,由力的平衡得式(2):
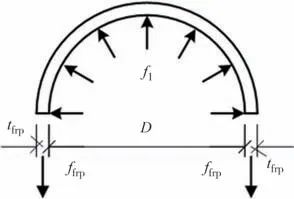
图6 CFRP布约束柱受力分析Fig.6 Force analysis of CFRP confined column
式中:εfrp为CFRP 布的横向应变.tfrp为CFRP 布的厚度,当CFRP 布粘贴多层时,取CFRP 布总厚度;当CFRP 布采用间隔包时,考虑CFRP 布的有效约束系数,计算确定CFRP 布的有效约束应力,从而可以将间隔包换算成全包时的等效厚度.
3 复合加固方形木柱侧向承载力计算
3.1 计算假定
在推导内嵌钢筋外包CFRP 布复合加固方形木柱侧向承载力公式时,给出如下假定:
1)木柱顺纹本构为理想的弹塑性模型;
2)木材、加固材料的截面应变符合平截面假定;
3)忽略木材弹性模量拉、压、弯状态下的差异;
4)木材为理想材质,忽略木材木节、裂缝等天然缺陷的影响;
5)不考虑CFRP布的抗压强度;
6)加载过程中,内嵌钢筋与木材黏结可靠,不发生滑移,钢筋、植筋胶与木材在竖向保持应变协调,CFRP布与木材在横向保持应变协调.
3.2 复合加固方形木柱侧向承载力计算方法
试验研究表明,本文试件均发生受拉破坏.因木柱的受拉强度一般为其受压强度的2~3 倍,故在达到极限状态时木柱受压区域早已进入塑性.根据相关研究[23-24],木材极限压应变和屈服压应变之比为3.3,即εcu/εcy=3.3.
截面内力分析如图7 所示.e为截面轴力作用点至受拉区合力作用点的距离,e0为轴力偏心距.y为受拉区高度,x为受压屈服段高度,xc为受压未屈服段高度.εt为木材极限拉应变,β为木材的压拉强度比,即β=fcy/ft.参考混凝土柱大偏心受压,给出本文试件的侧向承载力计算方法:

图7 截面内力分析Fig.7 Section internal force analysis
式 中:Fcu=fcybx;Fcy=fcybxc/2;Ft=ftby/2;;Fs=σsAs;L为木柱高度;d为钢筋直径;当试件被CFRP布加固时,fcy即为加固后木柱的顺纹抗压强度fcc,fcc根据上文给出的方法计算;σs'和σs分别为受压钢筋和受拉钢筋的应力;As'和As分别为受压钢筋和受拉钢筋的截面面积.
在综合考虑了木材的各向异性及天然缺陷、木材与钢筋之间黏结效应、CFRP 布与木材间变形协调等影响因素的情况下,引入修正系数,对复合加固方形木柱承载力计算公式进行修正,试验值与理论值的关系曲线如图8 所示.对试验值和理论值进行回归分析,得到修正后的复合加固方形木柱侧向承载力的计算表达式:
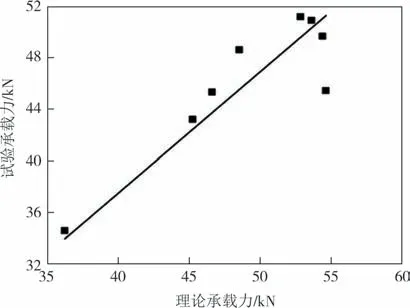
图8 承载力拟合曲线Fig.8 Fitting curve of bearing capacity
式中:0.939为回归得到的修正系数.
3.3 复合加固方形木柱侧向承载力计算结果比较
根据公式(9)计算所得的各试件侧向承载力列于表5 中,可以看出,通过理论公式得到的各试件的侧向承载力计算结果与试验值较为接近.
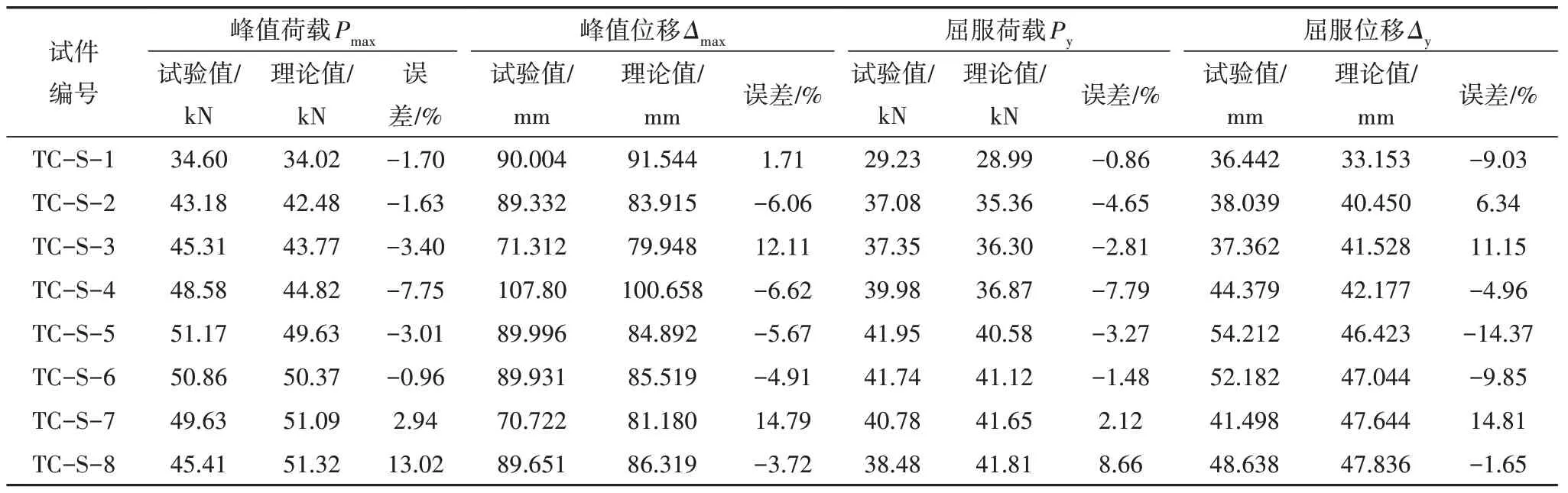
表5 计算值与试验结果的对比Tab.5 Comparison between calculated and experimental results
4 复合加固方形木柱的恢复力模型
恢复力模型描述了低周往复荷载作用下构件的延性、变形、刚度和耗能等特征的变化规律,常用恢复力曲线表示,本文选用三折线模型对试验所得滞回曲线进行简化.恢复力曲线主要由骨架曲线和滞回规则组成,骨架曲线是指滞回曲线中每个循环峰值点的连线,滞回规则是指模型正负向加载和卸载的路径以及刚度、强度退化规律.
4.1 骨架曲线
根据试验得到的复合加固方形木柱的骨架曲线,将其简化为理想三折线骨架曲线.骨架曲线的第一段为弹性段,刚度K1=Py/Δy;第二段为强化段,屈服点和承载力峰值点之间的直线段,刚度K2=(Pmax-Py)/(Δmax-Δy);第三段为强度下降段,承载力峰值点与85%承载力点之间的直线段,刚度K3=(Pmax-Pu)/(Δu-Δmax).
骨架曲线的三个特征点分别为屈服点、峰值点和破坏点,它们所对应的屈服荷载Py、屈服位移Δy、峰值荷载Pmax、峰值位移Δmax、极限荷载Pu、极限位移Δu是确定骨架曲线的关键参数.
弹性段轴向荷载对方形木柱侧向受力影响较小,故只考虑水平荷载的影响.参考悬臂梁挠度计算公式,并对其进行修正得到屈服位移计算公式:
式中:E为抗弯弹性模量;H为柱高;I为截面惯性矩;Py为屈服荷载.屈服位移的试验值与理论值的关系曲线如图9所示.
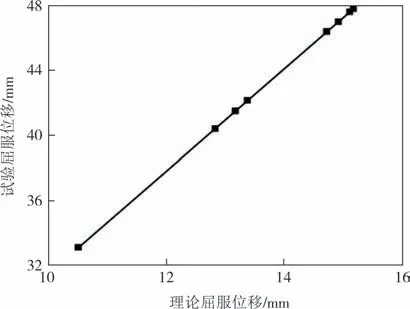
图9 屈服位移拟合曲线Fig.9 Fitting curve of yield displacement
考虑配筋率对屈服荷载Py和峰值荷载Pmax之间关系的影响,通过试验数据回归分析得到屈服荷载Py的计算公式:
式中:ρ为配筋率.
在计算峰值点位移时,需要考虑弯曲、剪切、滑移、二阶效应等影响因素,而且木材的材性离散性较大,故荷载峰值点对应的位移Δmax采用试验数据回归方法确定.考虑配筋率ρ对峰值位移Δmax和屈服位移Δy之间关系的影响,通过对试验数据进行回归分析得到峰值位移Δmax的计算公式:
从表5 可看出,计算值和试验结果吻合良好,上述公式能够较好地预测各试件的屈服荷载Py、屈服位移Δy和峰值位移Δmax.
4.2 卸载刚度
在试件屈服后,当卸载或改变荷载方向且未发生新的位移前,恢复力会出现突然松弛的现象,卸载段基本上与纵坐标平行,该现象称为位移滞后.这是因为其恢复力是由木柱受弯变形而产生的,当位移方向改变时,受弯变形消失,恢复力随之消失.这种现象加大了滞回耗能,是中国古建筑结构抗震耗能性能好的主要原因之一.本文试件卸载时,恢复力先产生松弛,卸载段的变化量是30%~42%.卸载段结束后按切线刚度Ku卸载至零,之后反向加载至交点处,这一段表现出明显滑移现象,使得滞回曲线形成一定的捏拢形状.
4.3 反复加载路径及强度退化
试件的滞回曲线存在上下两个交点,这两个交点大部分位于纵坐标轴上,每一级的滞回环相交于这两个点.卸载后的反向加载或再加载路径首先指向交点,之后由于强度退化,指向历史最大位移点对应的强度退化点.
4.4 滞回规则
图10 为试件的三折线恢复力模型,结合上述分析,总结出复合加固方形木柱的滞回规则:
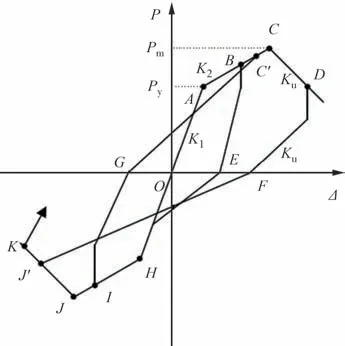
图10 复合加固方形木柱恢复力模型Fig.10 Restorony force model of composite strengthened square timber columns
1)弹性段加载和卸载的规则,即在复合加固方形木柱恢复力未超过屈服强度之前,其加载和卸载路径均沿着骨架曲线进行(图10中OA段).
2)复合加固方柱受力超过名义屈服强度之后,加载路径沿着骨架曲线进行(图10 中AB段和HI段);卸载时先经过恢复力松弛段之后按卸载刚度Ku卸载至位移轴(图10中BE段).
3)正向卸载以后,反向加载时先从位移轴加载至交点,再指向最大位移对应的强度退化点(图10中C'和J').
4.5 骨架曲线对比
通过本文给出的恢复力模型,计算得出了各试件的骨架曲线,如图11 所示,并将其与试验所得骨架曲线进行了对比.理论计算骨架曲线弹性段与试验骨架曲线弹性段吻合良好;第二段强化段和第三段下降段,除试件TC-S-8 外均吻合较好.经观察试件TC-S-8 破坏部位,发现该木柱破坏处有木节存在,本身缺陷较多,故其承载力较低,刚度下降较为明显.计算时无法考虑到每一根木柱的初始缺陷,故理论计算试件TC-S-8 的骨架曲线与试验曲线有所偏差.恢复力模型与试验结果吻合良好,能够反映复合加固方形木柱的滞回性能.
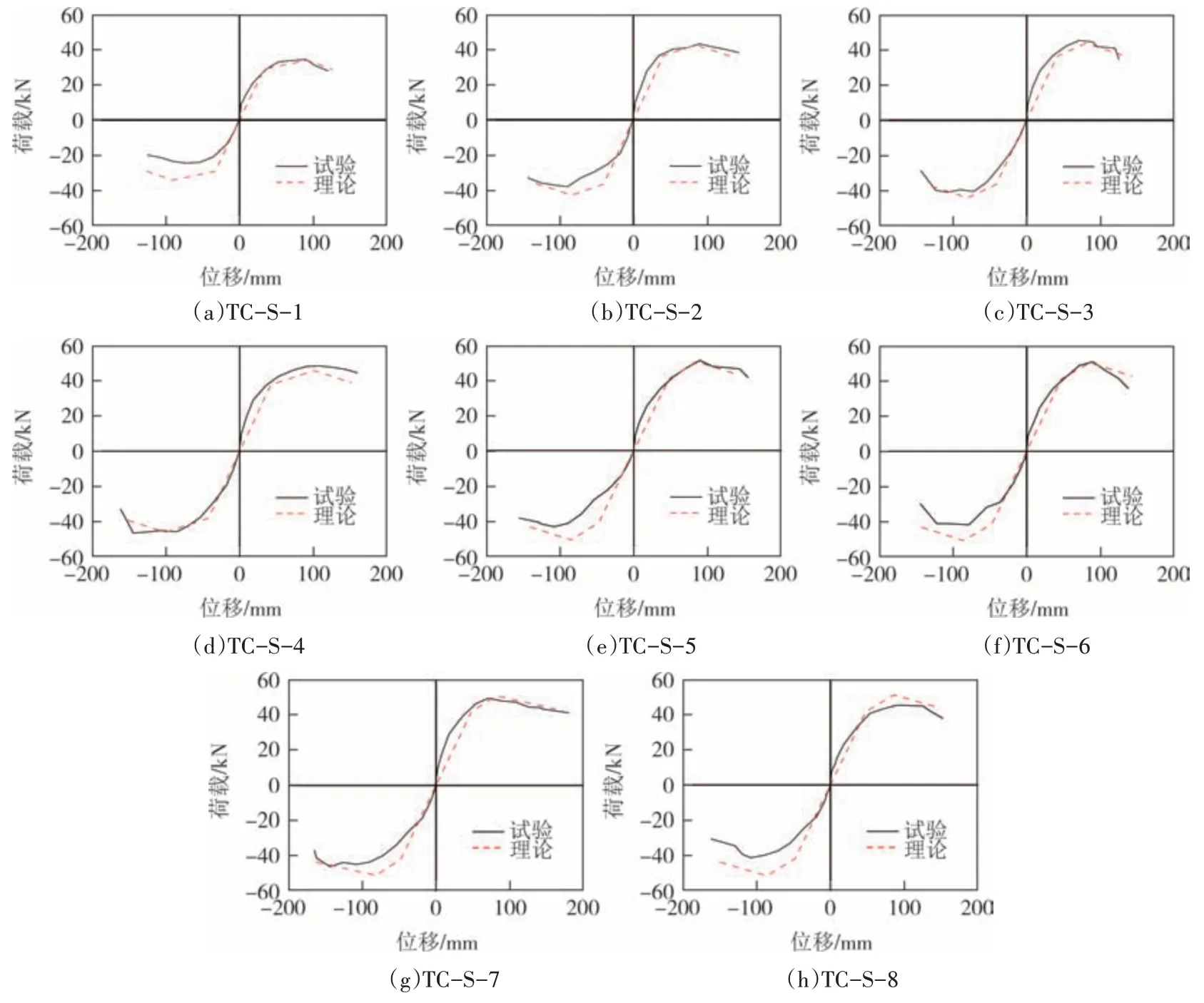
图11 试件理论骨架曲线与试验结果对比Fig.11 Comparison of skeleton curves between theoretical and experimental results
5 结论
本文基于内嵌钢筋外包CFRP 布复合加固方形木柱的低周往复荷载试验结果,参考CFRP布约束混凝土矩形柱的强度计算模型,综合考虑CFRP布加固量和钢筋用量对复合加固方形木柱的影响,给出了复合加固方形木柱的恢复力模型,得到以下的主要结论:
1)内嵌钢筋外包CFRP 布复合加固方形木柱的抗震性能显著提升,试件侧向承载力大幅增长,承载力下降更加缓慢,滞回曲线的捏拢现象明显改善,滞回环更为饱满,试件整体耗能能力更强.
2)给出CFRP 布约束方形木柱强度计算方法和内嵌钢筋外包CFRP 布复合加固方形木柱侧向承载力计算公式,确定了复合加固木柱三折线骨架曲线模型和骨架曲线各特征点的计算公式,理论计算与试验结果吻合良好.
3)提出了内嵌钢筋外包CFRP 布复合加固方形木柱的恢复力模型,较好地反映了内嵌钢筋增强与外包CFRP布约束对木柱滞回性能的影响,为复合加固木柱的抗震分析和工程应用提供理论支撑.
