水平激振下饱和土中楔形桩动力阻抗分析

胡安峰，陈正，肖志荣，谢森林，陈奕扬

（1.浙江大学 滨海和城市岩土工程研究中心，浙江 杭州 310058；2.浙江科技学院 土木与建筑工程学院，浙江 杭州 310023）

近年来，一些异形桩因其各自的优点在工程中得到广泛应用，起源于20世纪80年代具有良好承载性能的楔形桩便是其中一种.国内外已有学者［1-4］进行楔形桩相关承载能力的研究，相较于等截面桩，楔形桩侧面受到地基土的法向力，不仅提供了向上的承载力，还提高了桩基的侧摩阻力，使桩基的承载性能有较大的提升.

在理论研究方面，蔡燕燕等［5］基于平面应变模型得出了楔形桩桩顶的纵向振动阻抗的解析解.吴文兵等［6-7］考虑了桩体横向惯性效应，利用Rayleigh-Love 杆模型拓展了楔形桩纵向振动理论，后利用剪切复刚度传递模型分析了桩侧土存在挤土效应下的楔形桩纵向振动特性.王奎华等［8］研究了考虑微元桩段环形凸面与土相互作用的楔形桩纵向振动特性.之后，高柳等［9］进一步分析了施工扰动效应下的楔形桩桩顶横向振动特性.王奎华等［10-11］结合试验研究完善了楔形桩的动力响应特性，又基于非等截面桩体模型，研究了缺陷楔形桩的纵向振动特性.杨紫健等［12］推导了在Winkler 模型下黏弹性地基中的楔形桩位移、弯矩等解析表达式，探讨了桩土设计参数对楔形桩时间与空间的响应影响.余俊等［13-15］在Biot 固结理论模型上对等截面桩做了较多研究，栾鲁宝等［16］进一步拓展推导得到考虑竖向荷载的桩基水平振动解析解.郑长杰等［17］基于土体三维波动理论分析了黏弹性地基中管桩的水平振动特性.

综上可以看出，基于动力Winkler 地基模型下的楔形桩理论研究已较为完善，而基于Biot 饱和多孔介质理论的楔形桩水平振动特性研究还相对少见.已有研究［18］指出，土体渗透性对桩基动力响应具有显著影响.相较于弹簧系数与黏壶系数采用经验值的Winkler 模型，Biot 饱和多孔介质理论考虑了土骨架与孔隙流体的相互作用，能更好地描述饱和土体的性质.因此，本文基于此理论建立桩-土耦合模型来研究楔形桩的水平振动特性，探究楔角、长径比以及土体渗透性对桩顶阻抗的影响.

1 数学模型

1.1 计算模型与假定

基于Biot 饱和多孔介质理论和Novak 薄层法建立楔形桩简化计算模型，桩顶所受的简谐激振为P⋅eiωt和M⋅eiωt，P为水平荷载，M为弯矩，i 为虚数单位，ω为圆频率，t为时间.等截面桩体模型是目前研究楔形桩动力响应的一种较成熟的方法［5-7，12］，楔形桩楔角为θ，将桩-土系统由顶部到底部共等分为j层微段，从上往下依次标序1，…，k，…，j（如图1所示），当桩-土系统分层数j足够大时，每层的微段桩体单元可看视作等截面圆柱体.桩长为H，桩底半径为rj，k层桩身微段半径为rk=rj+(1-k/j) ⋅H⋅tanθ.

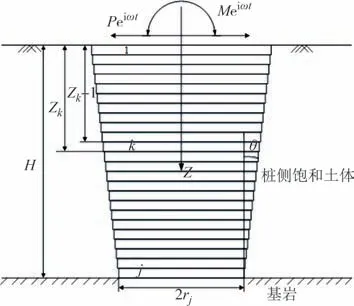
图1 楔形桩桩-土系统简化计算模型Fig.1 Simplified calculation model of pile-soil system of tapered pile

采用如下基本假定：

1）各层土体为饱和、均匀、各向同性的两相介质，由一系列相互独立的薄层组成，忽略土体的竖向连续性；

2）楔形桩为桩径自上而下逐渐变小的弹性杆件，底部刚性支承，不考虑桩土接触面间的摩阻力；

3）桩-土系统振动为小变形，桩土间完全接触，且接触面不透水；4）忽略楔形桩桩身顶、底所存在的微小突变，假设楔形桩桩身直径从顶部至底部均匀变小.

1.2 基本方程与边界条件

基于Biot 饱和多孔介质理论，可建立柱坐标下第k层桩周土的水平振动控制方程：

基于Euler 梁模型，土中k层桩段水平振动控制方程为：

式中：qsk为桩周土体动反力；Ep为桩体弹性模量；Ipk为桩段截面惯性矩；mpk为桩段单位长度质量；upk为k层桩段水平位移.

桩-土系统边界条件如下：

1）土体位移边界条件：

2）位移连续条件及渗透边界条件：

3）桩底位移边界条件：

式中：up为桩身位移.

2 方程求解

2.1 桩周土振动方程求解

引入位移势函数：

式中：φsk、ψsk、φfk、ψfk分别代表k层土体中土骨架与流体的位移势函数，其与r、θ相关，并包含时间因子项eiωt.

将其代入桩周土的水平振动控制方程，在后续的推导中可约去eiωt.利用分离变量法推得矩阵形式：

将式（10）及式（11）视为微分算子方程，要使方程有非零解，行列式为零，可得：

由微分算子分解理论，式（13）可分解为：

基于分离变量法，设φsk=φsk1+φsk2=R(r)Θ(θ)，结合桩土边界条件以及修正贝塞尔函数的性质，可得势函数如下：

式中：K1（*）为第二类修正贝塞尔函数.

同理可得流体相对于土骨架的位移wrk、wθk.

结合桩土接触条件以及渗透边界条件可得：

根据饱和土体本构关系可以确定土体应σr、τrθ和孔压pf，进而得到k层桩段周围土体水平动反力表达式：

2.2 桩基振动方程求解

桩基横向振动方程解为：

式中：ϑk=，Ep为桩体弹性模量；Ipk为桩段截面惯性矩；mpk为桩段单位长度质量；W1k、W2k、W3k、W4k为待定系数，并进一步得到如式（24）表示的k层桩段位移变形矩阵关系.

式（24）可转换为：

式中：[Sk(z)]为包含位移upk、转角φpk、弯矩Mpk、剪力Qpk的矩阵形式，[Sk(z)]=[upk(z)φpk(z)Mpk(z)Qpk(z)]T；[Xk]=[W1k W2k W3k W4k]T；[Γk(z)]为式（24）中的4×4矩阵.

则可得k段底端与顶端的位移、转角、弯矩、剪力关系满足：

而任意桩段交界面处的位移变形一致[Sk-1(zk-1)]=[Sk(zk-1)]，则通过矩阵传递可以得到完整桩段桩底（Sj）与桩顶（S1）的位移等变形的关系矩阵：

各阻抗表达式实部代表动刚度，虚部代表能量消散的动阻尼，将水平阻抗、摇摆阻抗无量纲化，可依次得到归一化后的水平动刚度Real(Kh)⋅、水平动阻尼、摇摆动刚度、摇摆动阻尼Imag(Kr)⋅，Ipj为桩底截面惯性矩.

3 桩土参数分析

假设桩周土为单一均质土，则桩-土系统计算参数如下：rj=0.5 m，H=10 m，θ=1°，ζk=0.01，αk=0.99，Mk=4.6 GPa，νk=0.35，nk=0.4，ρfk=1 000 kg/m3，ρsk=2 700 kg/m3，ρpk=2 500 kg/m3，Epk=30 GPa，Gk=10 MPa，kdk=10-6m/s，引入无量纲频率.从 图2中可看出，当桩段划分层数j达到100时，对桩体的阻抗结果影响不大.

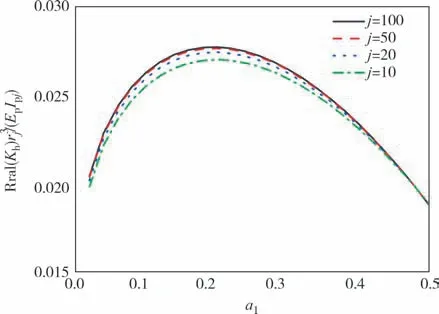
图2 桩体划分层数对计算精度的影响Fig.2 Influence of the number of pile layers on the calculation accuracy

3.1 桩体分层精度分析

在简化计算模型中，楔形桩被划分为j层直径自上而下均匀变化的等厚薄层单元段.桩体分层数会对计算结果产生重要影响，分层数量太少会影响计算精度，分层数过多将增加无效计算量，因此有必要对楔形桩的最优分层数进行分析.计算时H取15 m，楔角θ取2°，其余参数同上文.图2反映了桩-土系统划分层数j对桩顶动刚度的影响.可以看出当划分层数j达到50 时，计算结果趋于稳定.因此后续计算中，楔形桩划分层数取50.

3.2 模型退化验证

为验证本文楔形桩-土耦合振动阻抗解的正确性，将楔形桩退化为等截面桩（令θ=0°，ζk=0），与余俊等［13］解进行对比.计算参 数：n=0.375，H=20 m，其余参数同上.从图3中可以看出，两种模型振动阻抗解吻合较好，从而验证了本文解的合理性.

3.3 楔角对桩顶阻抗的影响

为研究楔角变化对楔形桩桩顶复阻抗的影响，保持楔形桩长度、桩底尺寸不变，楔角分别取：0°、0.5°、1.0°、1.5°.图4 和图5 反映了楔角对桩顶阻抗的影响.从图4和图5中可以看出，同一频率下，桩顶水平阻抗、摇摆阻抗随着楔角的增大而增大.增大楔角可以有效提高桩基动刚度和楔形桩-土系统的能量耗散速度.同时还可以看出，随着激振频率的增大，桩顶摇摆动刚度呈平缓增长的趋势，而大楔角楔形桩水平动刚度则先增大后减小.因此在风电等受到低频荷载作用的工程中可以增大楔形桩楔角以提高结构抵抗横向变形的稳定性.

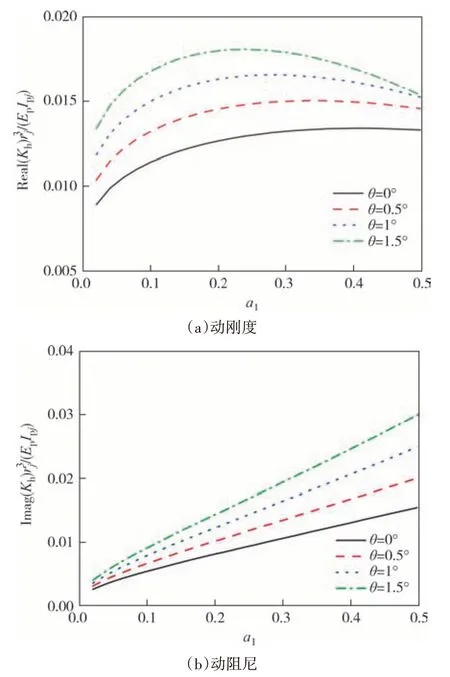
图4 楔角对桩顶水平阻抗的影响Fig.4 Effect of wedge angle on the horizontal impedance of pile head

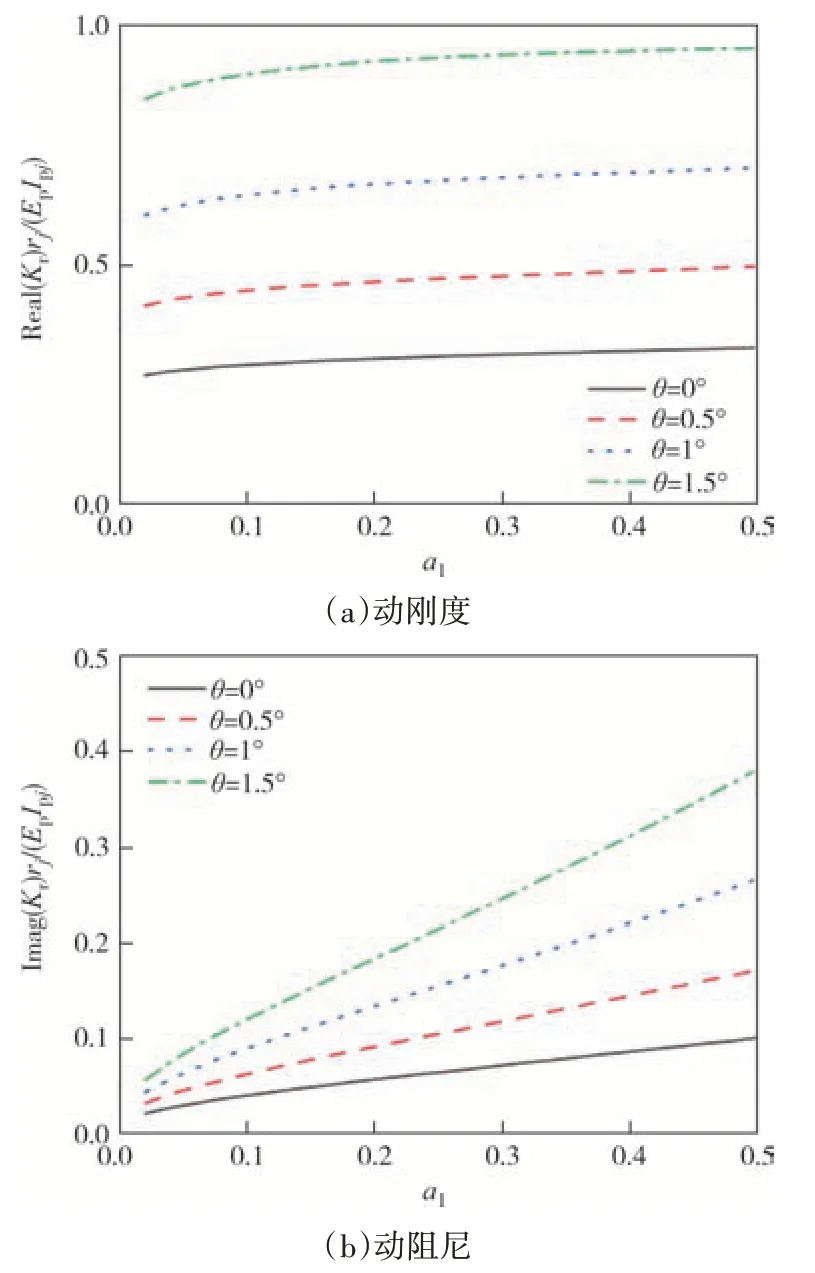
图5 楔角对桩顶摇摆阻抗的影响Fig.5 Effect of wedge angle on the rocking impedance of pile head

3.4 桩体长径比对桩顶阻抗的影响

图6 和图7 反映了楔形桩长径比对桩顶水平阻抗、摇摆阻抗的影响.保持楔角、桩底半径不变，长径比H/dj分别取：10、12、15、20.从图6 和图7 中看出，楔形桩水平阻抗、摇摆阻抗随长径比的增大而增大.相较于摇摆动刚度，长径比的改变对楔形桩水平动刚度的影响更复杂.不同长径比下的楔形桩摇摆动刚度随频率变化呈单调增大的趋势，水平动刚度则呈先增大后减小的趋势，且长径比越大，高频阶段水平动刚度随频率增大下降越明显.

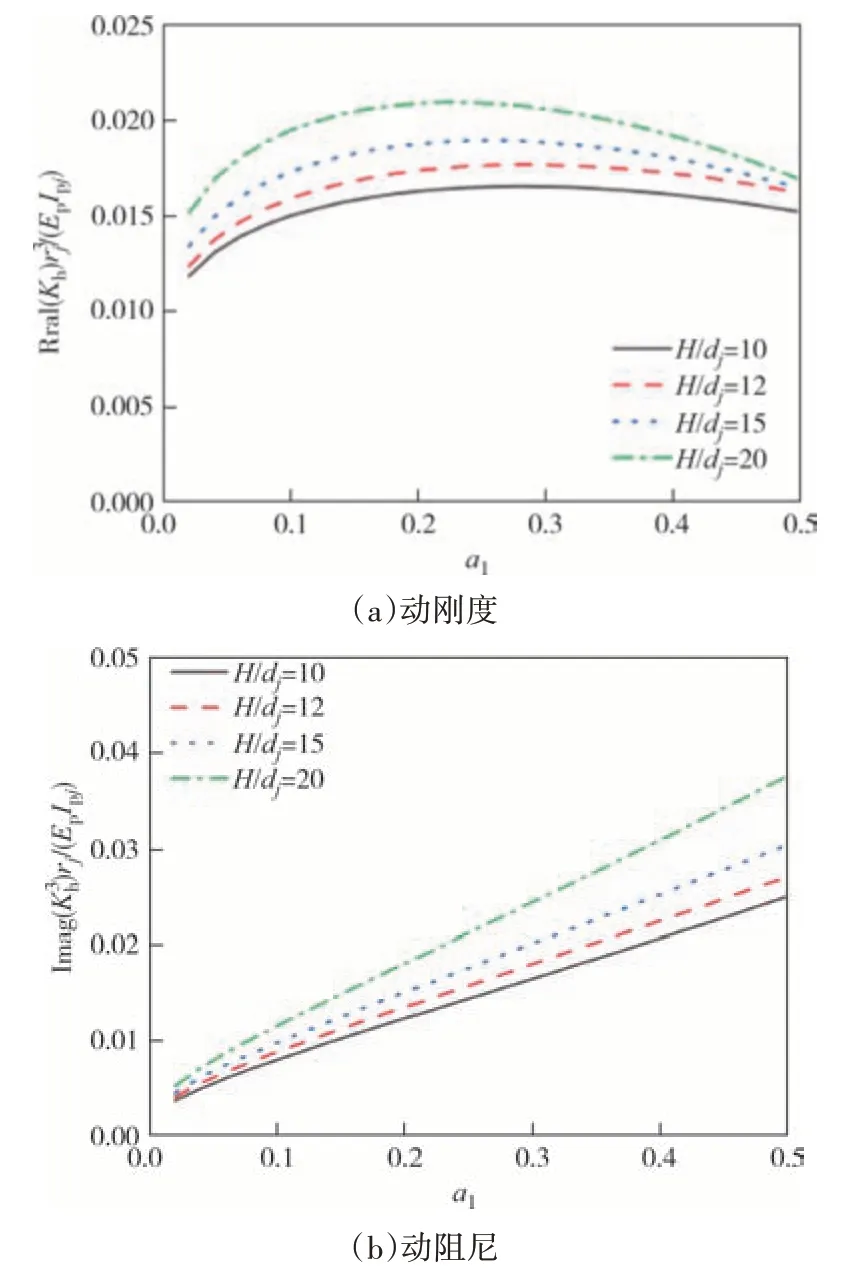
图6 长径比对桩顶水平阻抗的影响Fig.6 Effect of length of pile on the horizontal impedance of pile head

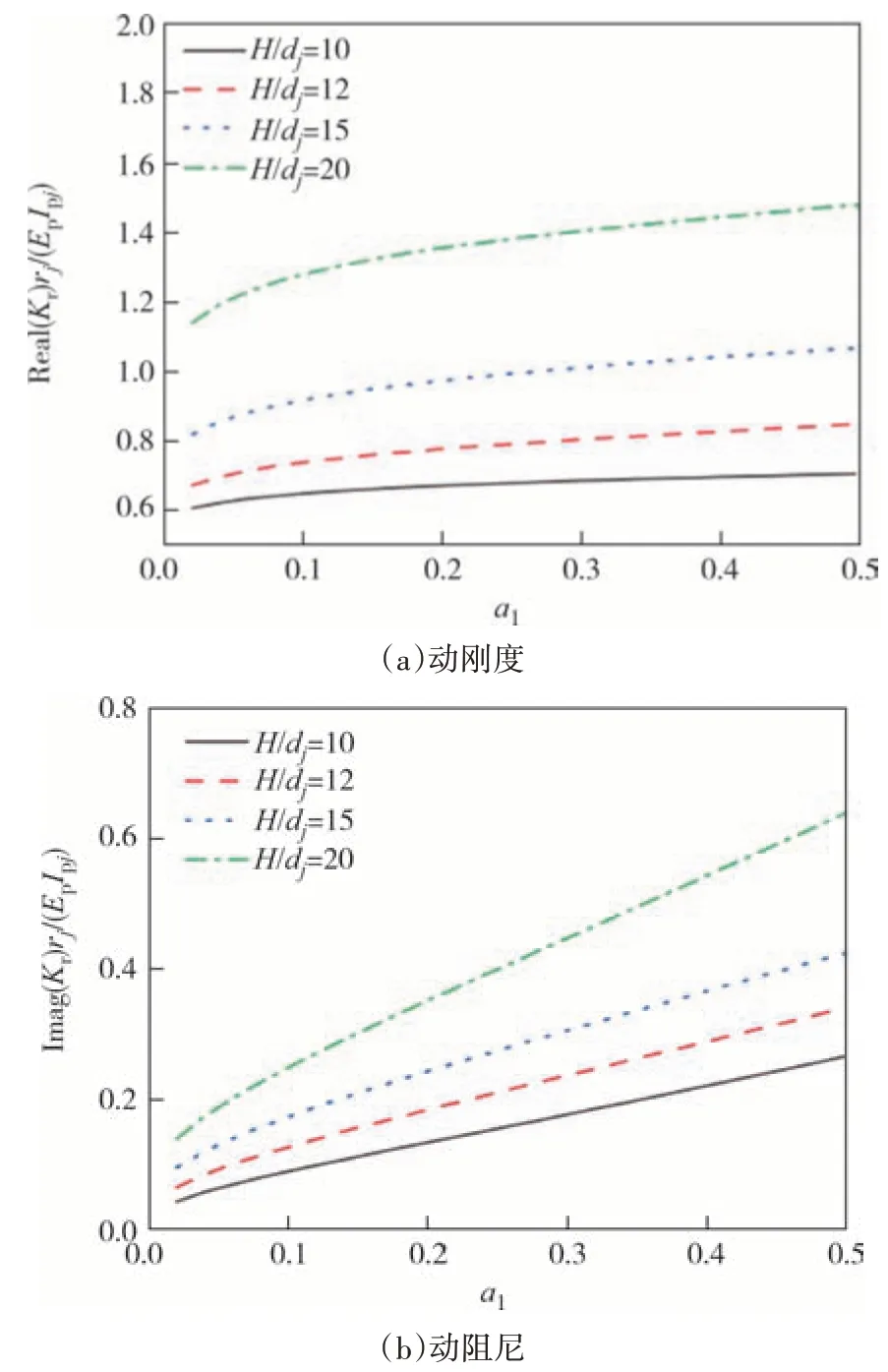
图7 长径比对桩顶摇摆阻抗的影响Fig.7 Effect of length of pile on the rocking impedance of pile head

3.5 等体积楔形桩水平振动特性分析

保持桩长、桩体中部截面尺寸不变，即楔形桩体积保持不变，研究不同楔角下的等体积楔形桩水平振动特性，桩基楔角分别取：0°、0.5°、1°、1.5°.从 图8和图9 可以看出，对于等体积楔形桩而言，在低频范围内，增大楔角可以提高桩基水平动阻抗和摇摆动阻抗.但是在高频阶段，楔形桩水平动刚度存在峰值，且随着楔角的增大，达到峰值后水平动刚度随频率下降趋势越明显.因此，在低频范围内，当混凝土用量有限且设计桩长一定，又对桩基水平承载能力有一定要求时，可以适当增大楔角以提高混凝土材料的使用效率.

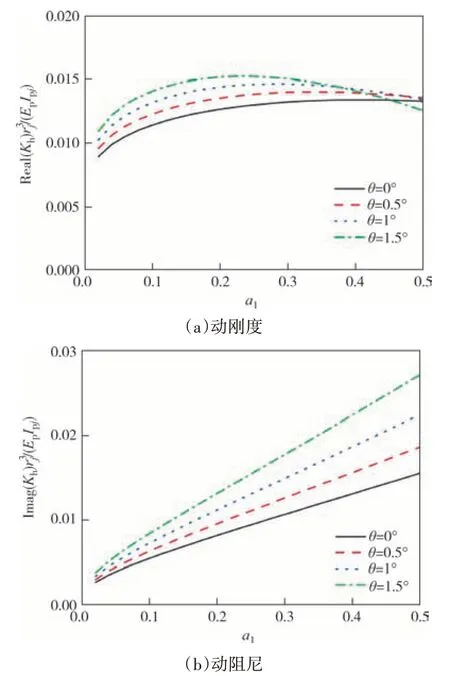
图8 等体积、不同楔角对桩顶水平阻抗的影响Fig.8 Effect of wedge angle length of pile with same volume on the horizontal impedance of pile head

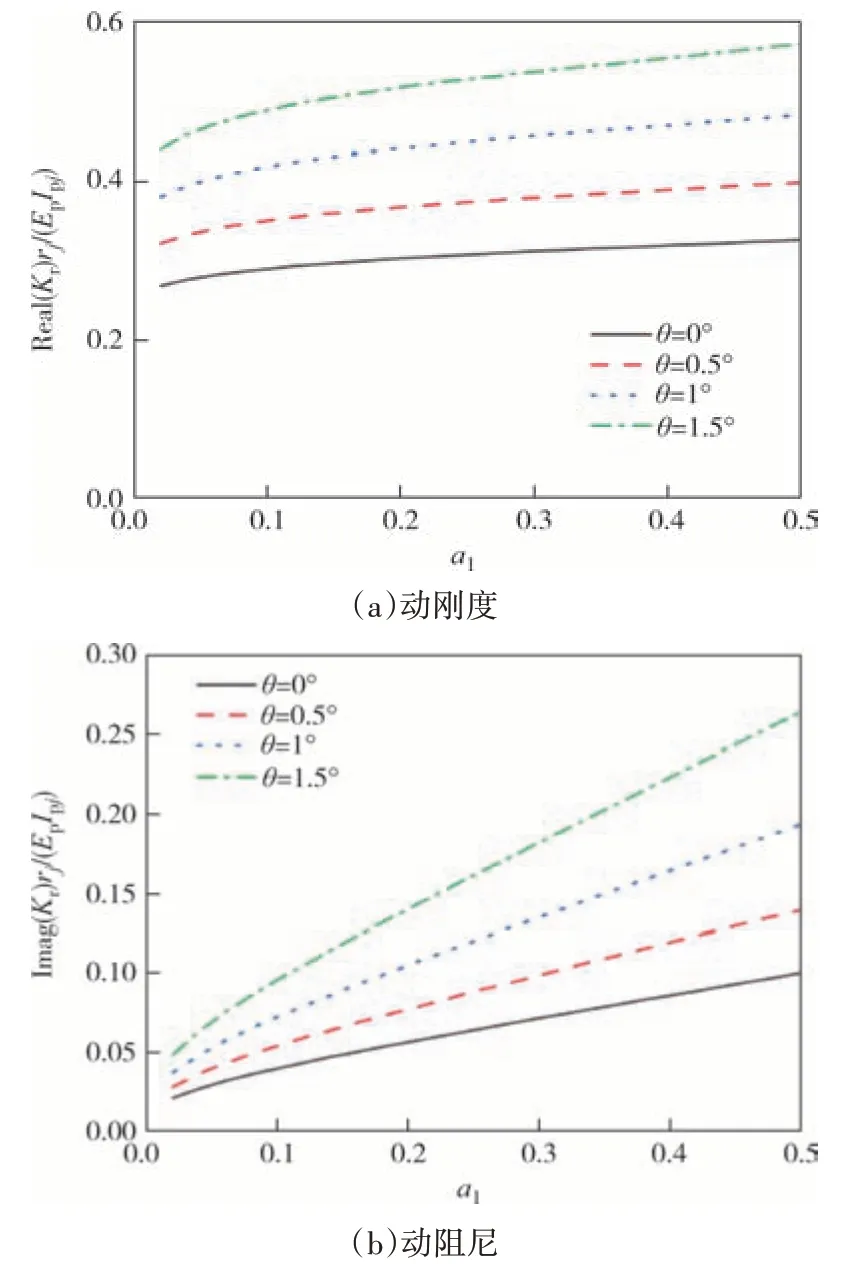
图9 等体积、不同楔角对桩顶摇摆阻抗的影响Fig.9 Effect of wedge angle length of pile with same volume on the rocking impedance of pile head

3.6 土中液相对桩顶阻抗的影响

图10 和图11 反映了桩周土中液相对楔形桩阻抗的影响.存在液相作用时，饱和土体中渗透系数分别 取：kd=10-2m/s、kd=10-3m/s、kd=10-4m/s、kd=10-5m/s、kd=10-6m/s，其余参数同上.从图10和图11中可以看出，饱和土中楔形桩动力阻抗随着土体渗透系数的减小而增大，当渗透系数减小至10-4m/s 以下时，渗透系数对桩顶阻抗的影响可以忽略不计.

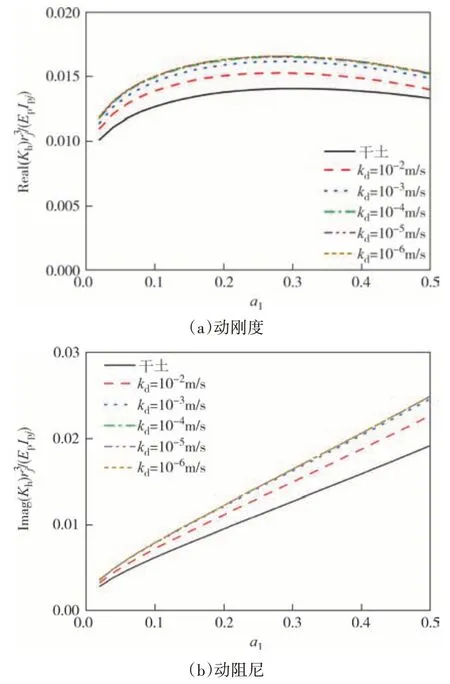
图10 土体渗透系数对桩顶水平阻抗的影响Fig.10 Effect of permeability of soil on the horizontal impedance of pile head

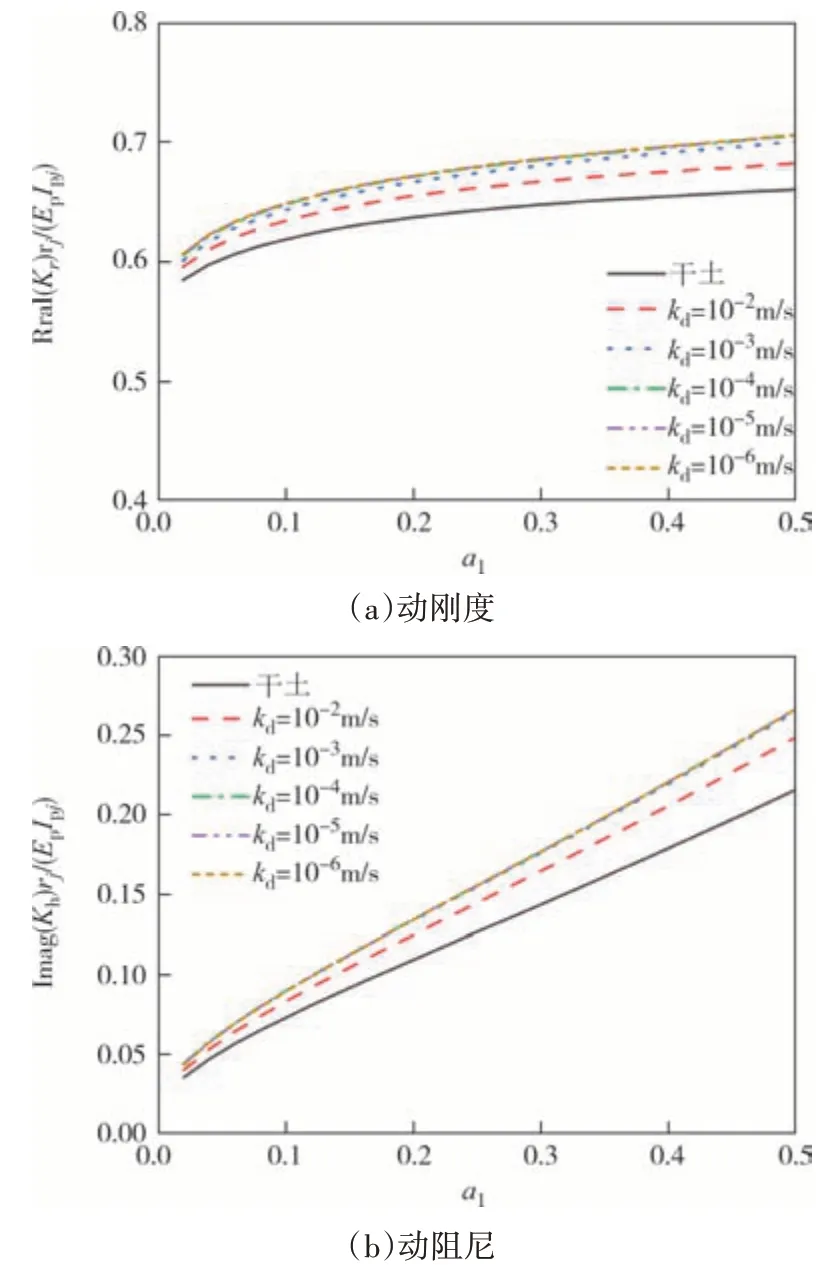
图11 土体渗透系数对桩顶摇摆阻抗的影响Fig.11 Effect of permeability of soil on the rocking impedance of pile head

土体密度ρ取与饱和土一致的密度值即 2 020 kg/m3，将方程中土体渗透系数kd、流体密度ρf数值取0，当将饱和地基退化为无液相作用的等密度干土时，楔形桩桩顶阻抗最小，这是由于单相土中不存在流体黏性耦合作用，而饱和地基中的孔隙水运动会导致能量耗散增加从而增大动力阻抗.

3.7 表层土层模量对桩顶阻抗的影响

由于天然土体的沉积作用，地基往往呈成层构造.图12和图13反映了上软下硬双层地基中上部土体模量对楔形桩动力阻抗的影响.两层土厚度一致取5 m，底层土剪切模量G2取20 MPa 保持不变.由图12 和图13 可知，桩顶动刚度随着表层软土模量的减小而显著减小，桩顶动阻尼在低频状态下也随表层软土模量减小而减小.因此，在实际工程中，需要对表层软土进行加固处理，以提高楔形桩的动力稳定性.

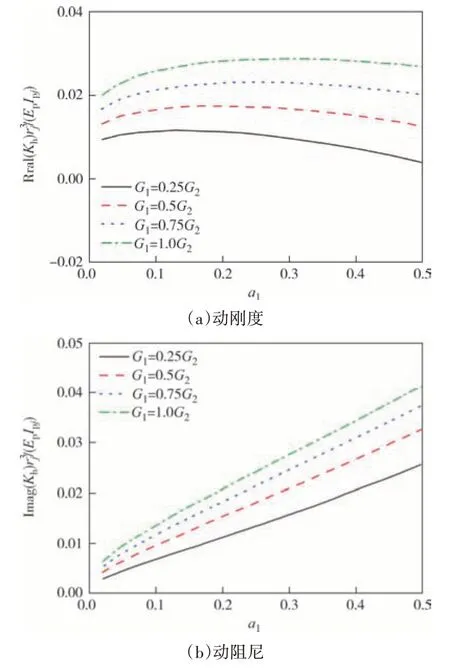
图12 表层软土模量对桩顶水平阻抗的影响Fig.12 Effect of modulus of soil on the horizontal impedance of pile head

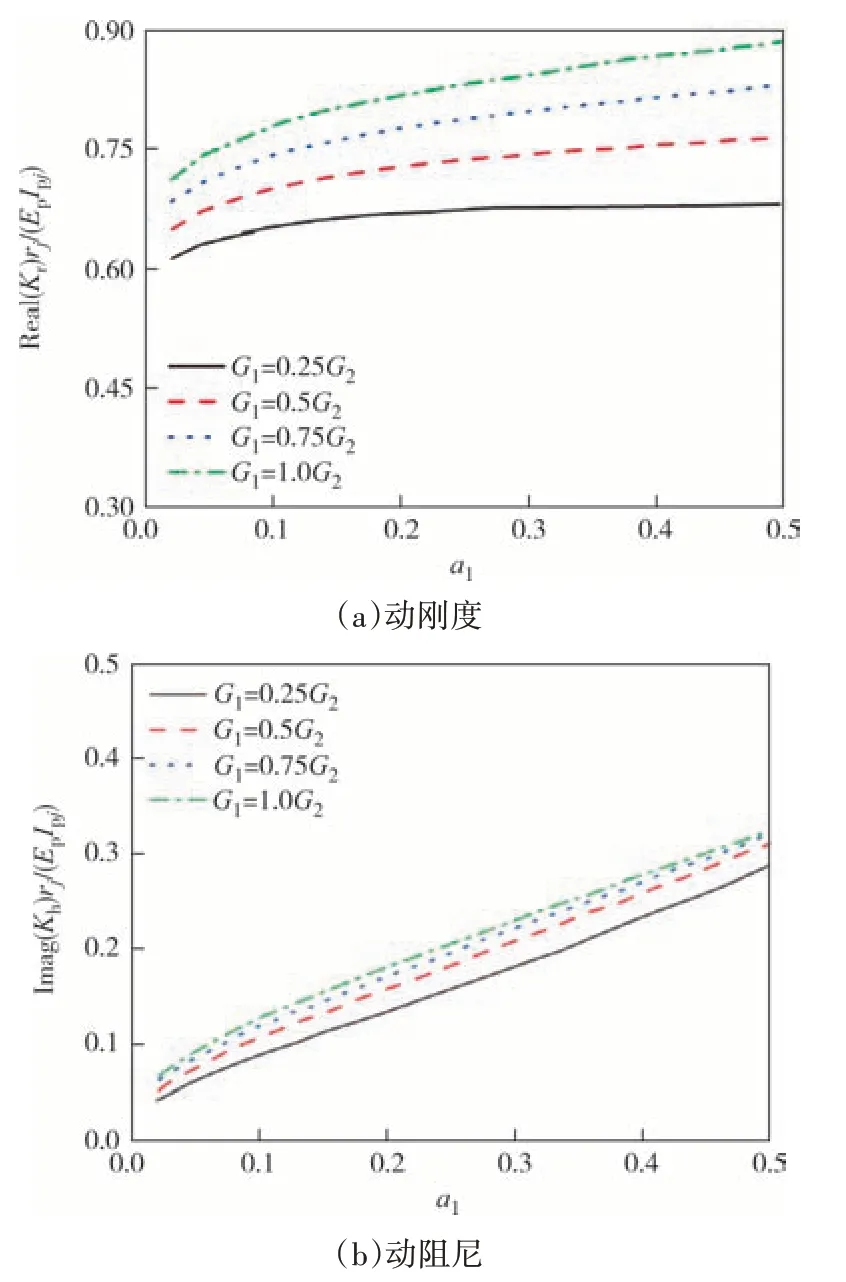
图13 表层软土模量对桩顶摇摆阻抗的影响Fig.13 Effect of modulus of soil on the rocking impedance of pile head

4 结论

将桩体等分为多个薄层单元段，基于Biot 多孔介质理论，建立了饱和土中楔形桩水平振动控制方程，得到了桩顶动力阻抗解析表达式，研究了桩-土系统划分精度对计算结果的影响，并通过退化对比，验证了本文解的合理性.最后通过算例分析，探讨了楔角、长径比、土中液相对桩顶动力阻抗的影响，得到以下主要结论：

1）桩顶水平阻抗、摇摆阻抗随着楔角的增大而增大.增大楔角可以有效提高桩基动刚度和楔形桩-土系统的能量耗散速度.随着激振频率的增大，桩顶摇摆动刚度呈平缓增长的趋势，而大楔角楔形桩水平动刚度则先增大后减小.

2）楔形桩水平阻抗、摇摆阻抗随长径比的增大而增大.不同长径比下的楔形桩摇摆动刚度随频率变化呈单调增大的趋势，水平动刚度则呈先增大后减小的趋势，且长径比越大，高频阶段水平动刚度随频率增大下降越明显.

3）对于等体积楔形桩而言，在低频范围内，增大楔角可以提高桩基水平动阻抗和摇摆动阻抗.但是在高频阶段，楔形桩水平动刚度存在峰值，且随着楔角的增大，达到峰值后水平动刚度随频率下降趋势越明显.

4）土体中液相的存在对楔形桩动力阻抗有显著影响，当渗透系数在10-4m/s 以下时，饱和土中楔形桩动力阻抗随着土体渗透系数的减小而增大；当土中不存在液相作用时，桩顶动力阻抗则会降低.

5）双层地基中，楔形桩桩顶阻抗受表层土体模量影响较大，桩顶动力阻抗随着表层软土模量的减小而减小，必要时需加固地基表层软土.