单位分数跨集中阻尼弦本征解的结构及其性质
2023-06-03郑罡王梦丽廖伟张晓东
郑罡,王梦丽,廖伟,张晓东
[省部共建山区桥梁及隧道工程国家重点实验室(重庆交通大学),重庆400074]
斜拉索的减振问题迄今仍是工程界重视的实际问题[1-2],在索端安装阻尼器对拉索低阶模态的减振效果已得到证明,并广泛用于工程实际中[3-5].随着斜拉桥跨度的增大,高阶模态的振动问题引起了新的重视[6-11],因此有必要进一步研究拉索-阻尼(器)系统本征解的结构及性质.
研究中常将拉索-阻尼(器)系统简化为带有集中阻尼的张紧弦[12-15],简称集中阻尼弦[16].就作者掌握的资料,文献[14-16]均给出了一致的超越函数形式的频率方程,鉴于求解超越方程的困难,文献[14]在阻尼(器)充分靠近弦端时,给出了近似条件下本征值的解析表达式;文献[15]以数值方法求得系统本征解,并绘制阻尼(器)位于有理数位置时的频率与阻尼(器)位置关系图;文献[16]给出了阻尼(器)位于跨中时的解析解.注意到,文献[14]引入了阻尼(器)位于弦端的假设,并在此假设下进行了近似解析求解;文献[15]用数值方法避开了超越方程解析求解的困难;文献[16]则针对单一案例(即集中阻尼位于跨中的情况),得到频率方程的代数形式.由上述文献成果可知,集中阻尼弦本征问题的困难仍集中于其超越方程的解析求解.注意到,文献[16]在特殊情况下首次得到了代数形式的频率方程,并求得该情况下的解析解,因此本文尝试利用频率方程代数化进一步探索解析求解的路径,以便于利用代数方程相关理论(如代数基本定理)实现该问题解析求解的突破.
同时注意到,文献[16]采用的方法仅适用于阻尼(器)位于跨中这一情况,对于其他情况[如本文所讨论的阻尼(器)位于1/n跨位置,且n≥3]不适用.因此,本文利用双曲函数多倍角公式突破文献[16]的频率方程代数化方法仅适用于单个案例(即集中阻尼位于跨中)的限制,使频率方程代数化过程适用于集中阻尼置于任意单位分数跨的情况.进一步,对于所得代数方程可解析求解的若干情形(即n=2,3,4,5时),求得集中阻尼弦本征问题封闭形式的解析解,当n=2 时,自然退化为文献[16]的结果.最后,基于新导出的代数方程和解析解,讨论解的结构和性质,从而克服了非解析方法(如文献[15]的数值方法)在讨论解的结构(如解支间的相互关系等)方面存在的固有困难.
1 问题描述
考虑的问题如图1 所示,其具有线质量密度,张力,弦长,阻尼(器)位于张紧弦上处,并且阻尼(器)位置满足

图1 带有集中阻尼的张紧弦Fig.1 A tension string with a lumped damping
该带有集中阻尼的张紧弦的自由振动方程可以写为[17]:
式中:为有量纲本征值. 引入以下无量纲参数和函数:
即可根据文献[16]的方法对图1 所示系统进行彻底的归一:
该归一化系统具有单位线质量密度m,单位张力T,单位弦长l,并在1/n跨位置设有线黏性阻尼(器),其频率方程为[16]:
式中:p为无量纲本征值,根据该方程知,其分母shp若为0,则方程无意义,而实际上,当shp为0 时,p为纯虚数,此时系统做无衰减自由振动,不受阻尼影响. 这类振动对应于阻尼(器)位置恰好为无阻尼弦自由振动本征函数驻点的情况,为文献[16]中讨论的Ⅱ类本征解,故本文对此类解不展开讨论,而重点研究分母shp不为0的情况,对应于阻尼(器)置于非无阻尼弦自由振动本征函数驻点,即Ⅰ类本征解.
由于复频率方程式(5)为超越方程,其一般通过数值手段求解.但在某些特殊情况下,即阻尼(器)位于单位分数跨时,可将复频率方程从超越方程形式转化为代数方程形式,从而利用代数基本定理对方程解的结构及其性质进行详细讨论.
2 复频率方程代数化
针对阻尼(器)位于弦单位分数跨的情况,将阻尼(器)位置xd=1/n代入复频率方程式(5)中,并化简得:
注意到式(6)中双曲函数自变量存在倍数关系.利用正弦函数倍角公式[18]以及双曲函数与三角函数的关系推得双曲正弦函数倍角公式:
根据双曲余弦函数ch(p/n)的性质知,其值必不为0,故令式(8)除以chn(p/n),则方程未知数仅为th(p/n):
注意到当th(p/n)为0 时等式始终成立,此时sh(p/n)为0,根据第1 节对其讨论可知,该解属于Ⅱ类本征解,故不再对此进行讨论.当其不为0 时,令z=th(p/n)得:
式中:ar为奇数次项系数;bm为偶数次项系数.
至此,复频率方程式(5)转化成关于z的n-1 次方程式(11),且此方程不存在零解.需要注意的是,该方程的解是关于阻尼系数的函数.
根据z=th(p/n),本征值p可有如下表达:
式(13)为对数函数,其具有多值特性.求解代数方程式(11),将其根代入式(13),可利用方程根的序列对本征值p的解进行归类,即所有本征值p可归为若干解分支,每一解支一一对应于代数方程的每一个根.这种解支关系称为解的结构.后文将从解的结构角度对集中阻尼弦系统进行研究.
3 解的结构与性质
根据代数基本定理的推论:复数域中,n次代数方程有且仅有n个根.则求解n-1 次代数方程式(11),可得n-1 个根,将其根代入本征值对数表达式(13)后,一个根可求出一组本征值,故频率方程有且仅有n-1 个解支,并且解支的具体个数与阻尼(器)布设位置有关.
本征值对数表达式(13)亦可写为复数形式p(i)=σ(i)+jω(i),其中j 为虚数单位,上标i表示第i个解支.由对数函数相关公式得本征值实、虚部表达式:
式中:常数s=0,±1,±2,±3,…;σ是本征值的实部,由于对数衰减率除以振动周期即为本征值实部的相反数,这表明本征值实部的相反数本质上是单位时间对数衰减率,故将本征值实部的相反数命名为单位时间对数衰减率,其符号记为“η”,代表单位时间内自由振动衰减的快慢;ω是本征值的虚部,为系统圆频率,简称频率.
对于系统的单位时间对数衰减率,由式(14a)可知:
1)当同时给定阻尼(器)位置与阻尼系数时,同一解支下的各阶本征值实部均相同,这表明该解支所表征的系统运动具有相同的单位时间对数衰减率,与模态阶次无关.
2)单位时间对数衰减率解的个数与解支个数一致,而解支的个数与阻尼(器)位置有关,故系统单位时间对数衰减率的具体个数与阻尼(器)位置有关,为n-1个.
结合上述两条发现,系统单位时间对数衰减率具有两条性质:一是单位时间对数衰减率解的个数有限,其具体个数与阻尼(器)位置有关;二是系统存在两阶幅值和能量衰减速度相同的模态.当系统第k1阶和第k2阶本征值同属于第i个解支时(k1>k2),两者单位时间对数衰减率相等,经过相同时间Δt时,两阶模态的位移响应幅值均按指数项eσΔt衰减,故两阶模态的幅值和能量衰减速度相等.
对于系统的频率,由式(14b)知:
1)同一解支下邻阶本征值的虚部差值相同,即各阶频率构成等差数列.该性质类似于无阻尼弦邻阶频率差值为(其中.注意到,由于布设了集中阻尼,任意解支下的各阶频率不再是某个频率(基频)的整数倍,但仍保留差值为常数的性质.
2)由于同一解支下邻阶本征值的虚部差值为常数,因此无法充分保证在单一解支内各阶本征值具有共轭性.实际上,这点是由代数方程根的性质决定的,即对于代数方程,若出现复根,则必为成对的共轭复根,这就意味着单一根所对应的解支通常无法满足共轭关系,需将方程另一共轭根对应的解支考虑在内,方可构成共轭关系.关于这点将在下文结合具体算例进行说明.
值得注意的是,结合上述关于单位时间对数衰减率与频率的讨论,对于任一解支下的各阶本征值,只需求得每一解支中的某一组单位时间对数衰减率和频率,即可得解支下完整的解.
上述关于系统单位时间对数衰减率和频率两者的讨论是从解的结构角度出发的,揭示了集中阻尼弦自由振动的一般通用性质.但注意到,两者的大小一般随着阻尼系数c的变化而变化,为进一步研究其性质,下文将利用代数方程式(11),从解析角度探究两者随阻尼系数c变化的规律.
可以发现,当n≤ 5时,代数方程式(11)为4次及以下方程,可由求根公式求得本征值闭合解,此有助于详细讨论本征值各解支的性质.表1 提供了n=2、3、4、5(即二分点跨、三分点跨、四分点跨和五分点跨)四个集中阻尼弦系统代数方程的系数,根据表1和代数方程相应的求根公式,即可求出系统本征值闭合解.

表1 代数方程系数表Tab.1 Coefficient of the algebraic equation
将表1 中的系数代入代数方程式(11)中,将求出的根代入本征值表达式(13)中,即可求得本征值的闭合解析解,图2~图5 分别为四个系统单位时间对数衰减率和频率随阻尼系数变化曲线.
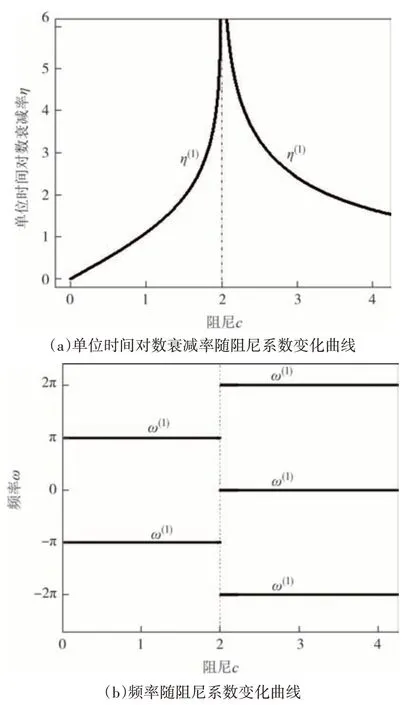
图2 二分点跨集中阻尼弦Fig.2 The taut string with a lumped damping at midspan

图3 三分点跨集中阻尼弦Fig.3 The taut string with a lumped damping at one-third-span
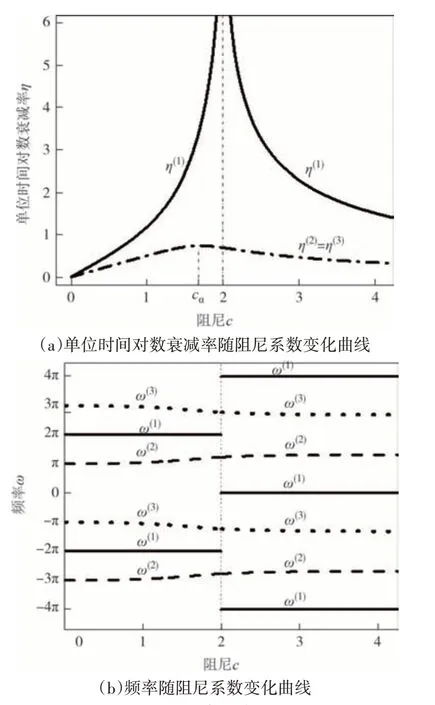
图4 四分点跨集中阻尼弦Fig.4 The taut string with a lumped damping at quarter-span
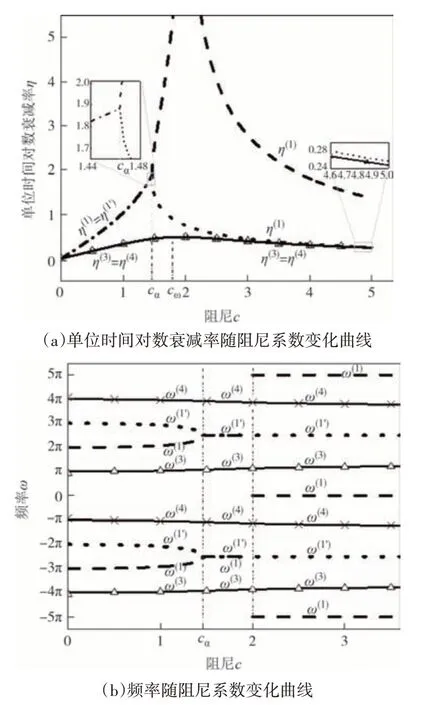
图5 五分点跨集中阻尼弦Fig.5 The taut string with a lumped damping at one-fifth-span
由图2(a)、图3(a)、图4(a)、图5(a)可知,上述四个系统均存在一特殊解支(记为p(1)),对于该解支下的单位时间对数衰减率,当阻尼系数从0 增加至2时,其从0 单调增加至无穷大;当阻尼系数从2 增加至无穷大时,其从无穷大单调减小至0.可以发现,当阻尼系数c取2 时,解支p(1)所表征的各阶运动将会瞬时衰减至0,阻尼振动将被瞬间抑制.
由图2(b)、图3(b)、图4(b)、图5(b)和频率表达式(14b)可知,对于特殊解支p(1)的频率,当c大于2时,其频率为常数snπ,当s=0 时,频率为0(系统做非震荡衰减运动).当阻尼系数c小于2 时,根据阻尼(器)位置的不同,频率出现不同现象:当n为偶数时,其为非零常数(s+1/2)nπ;n为奇数时,其在阻尼系数小于某一值(该值用cα表示,且cα< 2)时随阻尼变化,当阻尼系数在cα和2 之间时,其为非零常数(s+1/2)nπ,与n为偶数时一致.注意到,对于特殊解支p(1)出现常数的情况,其单位时间对数衰减率不为0,这点与阻尼(器)位于无阻尼弦驻点(频率同样为常数)的情况不同.
可以发现,当阻尼(器)位于奇数点时,除特殊解支p(1)的单位时间对数衰减率在阻尼系数c取2 时存在无穷大不可导点外,还出现了一新解支的单位时间对数衰减率,在阻尼系数c取cα时同样不可导(记为p(1'),以此代替p(2)).解支p(1')的单位时间对数衰减率,在阻尼系数c从0增加至cα时,从0单调增加至最大值;在阻尼系数c从cα增加至无穷大时,其从最大值单调减小至0.其频率在阻尼系数小于cα时随阻尼系数变化,在阻尼系数大于cα时为非零常数n(s+1/2)π.
值得注意的是,在此阻尼(器)位置条件下,解支p(1)和解支p(1')在阻尼系数c小于cα时互为共轭解支,即此时两者单位时间对数衰减率相同,频率互为相反数;当阻尼系数c在cα和2 之间时,两者不再共轭,前者单位时间对数衰减率随阻尼系数的增大而增大,后者单位时间对数衰减率随阻尼系数的增大而减小,但两者频率为相等的常数;当阻尼系数超过2时,两解支的频率仍为常数,但值不相同.
当n大于3 时,出现了一类新的解支,其单位时间对数衰减率随阻尼系数的变化而变化,在阻尼系数c取cω(cω≠cα)时,取得最大值;其频率亦随阻尼系数连续变化.同时注意到,该类型的解支均两两以共轭对形式出现,且对于任意阻尼系数都成立.
结合上述关于解支的讨论,根据其随阻尼系数变化的特点,可将其归纳为3 类:第一类解支的频率均依赖于阻尼(例如四分点跨系统的解支p(2)和p(3),五分点跨系统的解支p(3)和p(4));第二类解支的频率均不受阻尼影响(例如二分点跨情况下的解支p(1),四分点跨情况下的解支p(1));第三类解支综合第一类和第二类解支特点,频率在一定范围内(0<c<cα)与阻尼系数取值有关,一定范围内(cα<c)为常数(例如三分点跨情况下的解支p(1)和p(1'),五分点跨情况下的解支p(1)和p(1')).
实际上,三类解支与复频率代数方程式(11)的根的情况一一对应:第一类解支对应于方程的共轭复根,故该类解支以共轭解支对形式出现,解支个数必为偶数,且此类解支仅当n≥ 4 后才会出现;第二类解支对应于方程的实根,对于任意阻尼系数,该实根均为负实根,此类解支仅当n为偶数时才会出现;第三类解支亦对应于方程的实根,但与第二类解支不同的是,该根的情况随阻尼系数而变化,其在一定阻尼系数范围内(0<c<cα)为复数根,而在另一阻尼系数范围(cα<c)内为实数根,故该类解支亦两两成对出现,并在一定阻尼系数范围内,互为共轭解支,此类解支仅当n为奇数时才会出现.
将这三类解支的频率与阻尼(器)位置的关系与文献[15]进行对照发现(图6),第一类解支对应于区域1和区域3,当阻尼系数从0增加至无穷大时,其阻尼比从0 增加至最大值后再减小至接近0;第二类解支对应于1 类和2 类垂直解,当阻尼系数从0 增加至无穷大时,其阻尼比从0 增加至1;第三类解支对应于中间特例,即区域1 与区域2、区域3 与区域2 的交界线,由于此类解支均两两成共轭对形式出现,故其阻尼比需两两一对进行讨论,在阻尼系数从0 增加至无穷大时,两相邻阶阻尼比从0 开始增加,在中间某一点相交后,其中一阶阻尼比减小至接近0,另一阶阻尼比增加至1,综合了第一类和第二类解支阻尼比的特点.
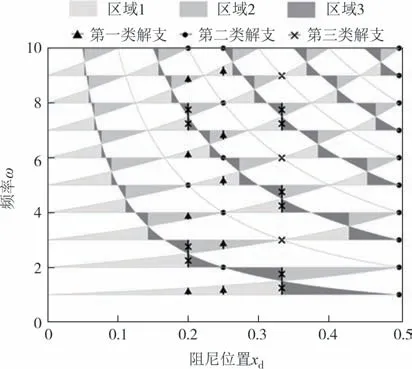
图6 三类解支的ω-xd关系与文献[15]的对比图Fig.6 Comparison of the ω-xd relation of the three types solution branches with reference [15]
4 结论
本文在阻尼(器)位于单位分数跨的条件下,推导出关于频率方程的代数方程形式,根据代数方程的相关性质,从解的结构角度对集中阻尼弦系统进行讨论,结果表明:
1)系统所有本征解可归为n-1 个解支,且解支的具体个数与阻尼(器)位置有关.
2)对于同一解支,各阶本征值实部(其相反数即单位时间对数衰减率)均相同,各阶本征值虚部(即频率)构成等差数列.
根据具体算例,从解析角度进一步探讨了本征值随阻尼系数变化的规律,并将所有解支归结于三类进行讨论,结果表明:
1)第一类解支的频率均依赖于阻尼.该类解支对应于代数方程的共轭复根,均以共轭形式出现,仅当n≥4时才会出现,且解支个数为偶数.
2)第二类解支的频率均不受阻尼影响.该解支对应于代数方程的负实根,仅当n为偶数时才会出现,其有且只有1个.
3)第三类解支综合第一类和第二类解支特点,频率在一定范围内(0 <c<cα)与阻尼系数取值有关,一定范围内(cα<c)为常数.该类解支对应代数方程的根在0 <c<cα时为共轭复根,cα<c时为实根,且仅当n≥4时才会出现.
