空间弧形抗滑桩支护结构模型试验及参数分析
2023-06-03邓友生彭程谱杨彪孟丽青冯爱林
邓友生,彭程谱,杨彪,孟丽青,冯爱林
(西安科技大学 桩承结构研究中心,陕西 西安 710054)
滑坡是我国比较频发的灾害之一。滑坡的形成分为自然演变和人为诱发2类。随着我国大规模基础设施的建设和矿产资源的开发,后者产生的滑坡灾害在不断增加。滑坡治理的方法主要有:排水、清方减荷、反压、支挡结构。其中,抗滑桩以其良好的支护效果得到广泛的运用,抗滑桩通过嵌入滑动面以下,依靠自身刚度和桩前土压力抵抗滑体的下滑力。抗滑桩的结构形式不断优化,从结构受力简单的单排桩到双排桩,但其支护效果有限;沈简等[1]在一采用双排桩支护的边坡中,由于原支护结构支护能力不足,采用桩锚结构进行二次处理。为增大抗滑结构的刚度、稳定性和改善桩身受力状态,学者们不断研发了门式刚架抗滑结构[2]、由一对倾斜和竖直的桩组成的A型微型桩[3]、抗滑桩+支撑柱组合抗滑结构[4-5]、八字形微型桩群[6]。此外,拱是一种良好的受力结构形式,如地铁使用的桩梁拱法能很好地约束地表沉降[7]。平面弧形抗滑结构通过弧形冠梁将桩顶连系在一起,增大了结构的整体刚度,并充分利用滑体两侧稳定土体的抗力。文献[8-10]对平面弧形抗滑结构的组合形式、空间受力性能、变形特性及计算理论进行了详细的分析。以上研究表明:弧形抗滑支护结构可以改善抗滑桩的受力状态,约束桩顶位移,并充分利用了边坡滑体两侧稳定土体的抗力。但上述抗滑桩均布置在同一平面上,不利于适应边坡高程的变化和拱轴线矢跨比的调整。
抗滑桩的尺寸、桩的布置以及边坡的抗滑体系的支护效果有很大的影响。彭文哲等[11]通过建立有限元模型分析抗滑桩的最优桩位和桩长,并通过算例验证分析的合理性。Rao等[12]引入了三维上限极限分析法以评估边坡的稳定性,并考虑抗滑桩的影响,研究了不同土的非均匀性和各向异性对最优桩位和边坡稳定性的影响。Tang等[13]以抗滑桩桩顶位移为评价指标,分析了桩间距、锚固深度和桩体截面尺寸等因素对桩顶位移的影响。Wang等[14]采用运动极限分析方法,提出了一种局部分层求和法来考虑吸力对桩侧力的影响,当桩间距与桩径之比小于3且桩到坡脚的水平距离与坡面水平长度之比在0.6~0.7,抗滑效果更佳。
综上,在抗滑结构的发展过程中,从结构形式单一的悬臂式抗滑桩逐渐向桩锚或桩板式组合支护结构发展,但大多数边坡工程没有将所有的支护结构连系在一起。单排桩、多排桩通过冠梁将桩体连系在一起形成的整体抗滑结构,桩顶水平位移差异较大,冠梁容易因各桩顶之间的差异位移产生剪切破坏。平面弧形抗滑结构充分利用拱这一良好的支护结构形式,将拱脚布置在稳定土体中,充分利用了边界条件。但是,平面弧形抗滑结构在调整矢跨比的过程中需要较大面积的平整场地,在边坡实际工程中不易实现。
随着边坡稳定性问题的复杂化和滑坡推力的增加,从最开始的悬臂式抗滑桩到锚拉式抗滑桩、双排桩、双排门架式抗滑桩、A型桩、八字型桩、弧形桩等,大多数是通过增加附属结构、改变桩体刚度等,达到改善桩体的受力状态,减小桩顶水平位移的目的,而通过充分利用滑床周围稳定土体以抵抗土体下滑推力的研究较少。
本文提出空间弧形抗滑桩支护体系就是将桩布置在坡面及坡脚处,桩在平面上的投影呈弧形,冠梁沿着坡面将桩顶连接在一起,组成空间弧形抗滑桩支护体系。通过室内模型试验对支护体系的受力状态、荷载传递规律和桩前土压力进行了分析,验证结构的合理性和可行性;并分析抗滑结构的冠梁刚度、桩位对支护效果的影响规律。
1 模型试验
1)试验材料。
模型箱中土体采用黄土。边坡模型通过分层夯实,达到试验所需压实系数(λc≥0.9)。夯实后土体的基本的土性参数如表1所示。抗滑桩、冠梁使用304不锈钢,桩长如表2所示,其截面尺寸分别为40 mm×30 mm、30 mm×15 mm,壁厚1 mm,如图1、2。

图1 抗滑桩Fig.1 Anti-slide piles

图2 冠梁Fig.2 Couping beam

表1 土体参数Table 1 Parameters of soil

表2 抗滑桩桩长Table 2 Pile length
2)边坡模型。
综合考虑试验的可操作性、边坡与室内模型箱的尺寸以及试验的合理性,室内试验拟采用相似比为1∶10的模型作为研究对象。
室内试验采用的模型箱内空净尺寸为6 m×2.2 m×2 m,模型箱底部为地下原状土。边坡顶面长度2.2 m,宽度1 m,边坡坡度为60°,如图3所示。抗滑桩的布置如图4所示。冠梁通过焊接将各抗滑桩桩顶连接在一起,组成整个支护体系。
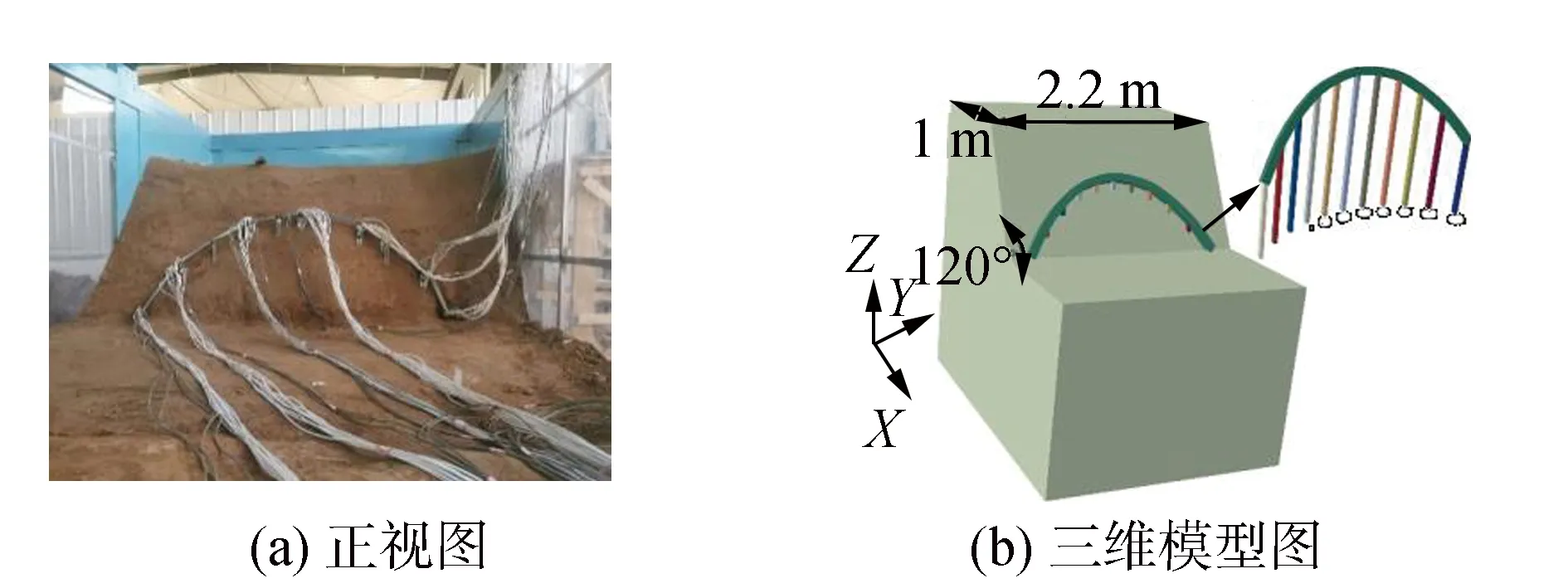
图3 边坡模型Fig.3 Slope model

图4 抗滑桩平面布置Fig.4 Plane layout of anti-slide piles
3)数据测量。
抗滑桩应变的采集使用BF1K-3EB全桥应变片。在P1、P2、P4的左右两侧布置应变片,在P6、P8、P10、P11的前后两侧布置应变片,应变片的布置如图5所示。数据采集系统选用TST3826E静态应变试验分析系统,分辨率可达1 με,数据采集为5 min/次。
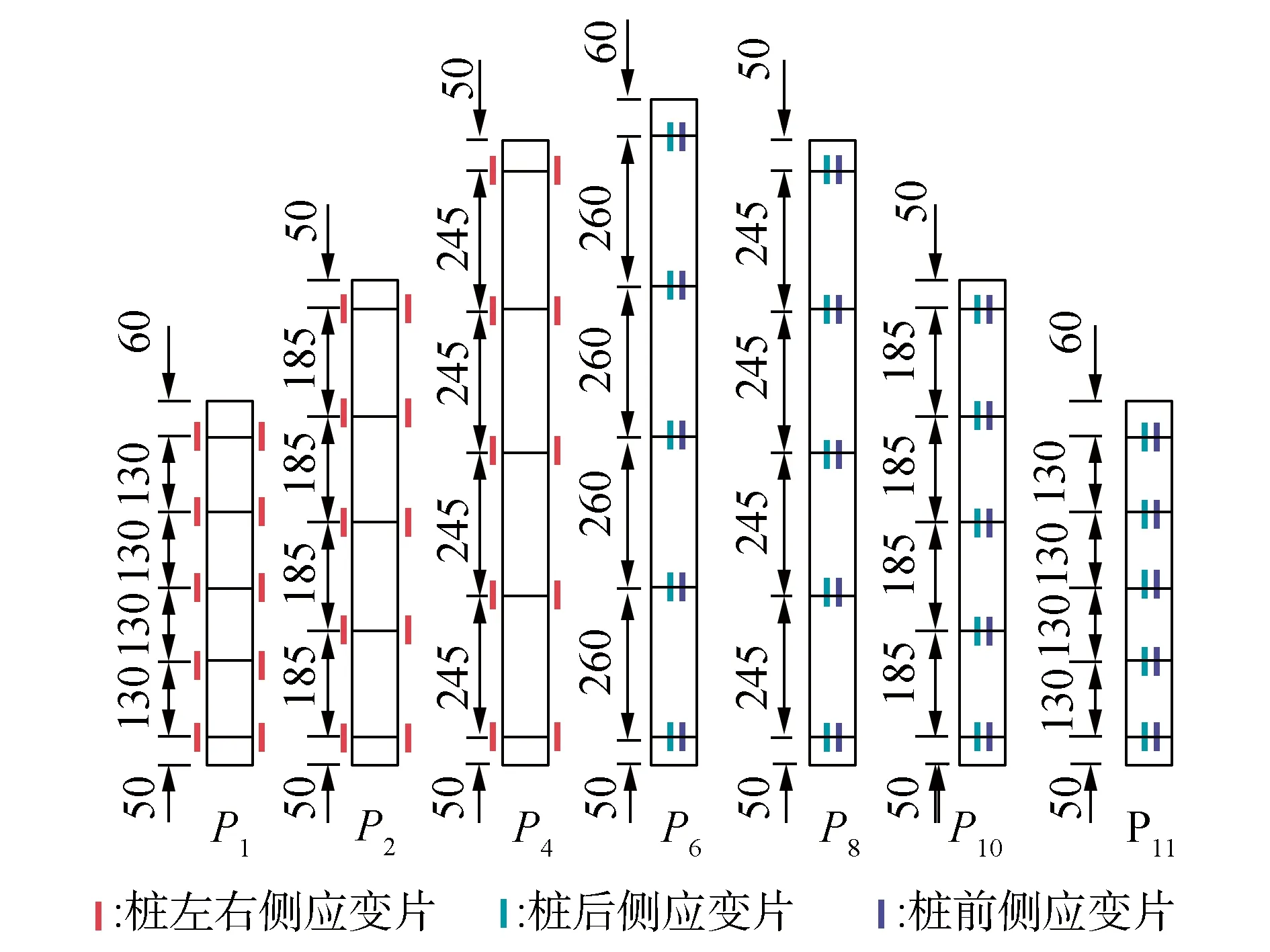
图5 应变片布置Fig.5 Distribution of strain gauge
土压力的测量采用YTDZ0301型应变式微型土压力盒,量程0.1 MPa。在土体分层填筑过程中,在P1、P4、P6的前侧预埋土压力盒,数据采集5 min/次。土压力盒布置图如图6所示。

图6 土压力盒布置Fig.6 Distribution of earth pressure cell
4)加载过程。
加载时,使用混凝土板当作外加荷载,混凝土板的尺寸为2 m×1 m×0.12 m,每块板为一级荷载,每级荷载为3 kPa(25×0.12=3 kPa),共5级荷载,如图7所示。每次加载完毕后,待应变采集系统中应变值稳定后,进行下一级加载。

图7 加载过程Fig.7 Loading process
2 试验结果分析
2.1 桩身弯矩
通过材料力学中截面弯矩与应变之间的转换公式,将采集的桩身截面应变转换成截面弯矩。在冠梁和抗滑桩组成的支护体系中,冠梁将力从中间抗滑桩向边桩传递,抗滑桩出现横坡向弯矩,P1、P2、P4横坡向的弯矩Mx如图8所示。各桩弯矩变化规律基本一致,最大值出现在桩顶;桩底弯矩较小,接近于零;桩底可视为铰接。桩中部出现正弯矩最大值。抗滑桩的受力状态类似一端固定、一端铰接的竖直梁。P1的桩顶弯矩最大,为287.58 N·m,P2次之,P4最小,冠梁将荷载向两端桩体传递,两端桩体充当拱脚作用。在传递荷载过程中,冠梁起到了桥梁的作用。由各桩桩顶弯矩的大小可知:冠梁在整个传递荷载的过程中受压,可以充分发挥混凝土的抗压性能,避免直线型冠梁中出现的剪切破坏。
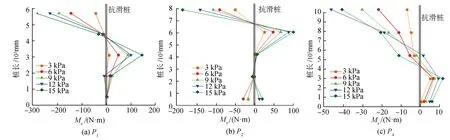
图8 MxFig.8 Mx
顺坡向的弯矩My的分布与Mx的分布不同,桩身弯矩为负,极少数截面弯矩为正值,如图9所示。此外,抗滑桩在顺坡向和横坡向弯矩出现峰值的位置不同。位于中间位置的桩体(P6、P8、P10),冠梁对桩顶的约束作用较明显,故弯矩最大值出现在桩顶以下截面,桩身受力状态得到改善;而边桩(P1)受冠梁传递荷载的影响,弯矩最大值出现在桩顶。在荷载作用下,各桩的弯矩峰值相近,波动范围在10%以内,体现了冠梁的变形协调作用。桩底的弯矩接近于零,可认为桩底为铰接。

图9 MyFig.9 My
2.2 桩前土压力
在荷载作用下,P1、P4、P6的桩前土压力如图10所示。P1的桩前土压力随着桩身高度的增大而增大,桩顶处土体的抗力达到最大值,第5级荷载时为1 425.8 Pa,充分利用了桩前稳定土体的支撑作用。P4、P6的桩前土压力在桩顶处较小,桩体中下部的土压力变化幅度小。在3根桩中,P1的桩顶处,土体抗力最大,其峰值是其他桩体土压力峰值的2倍以上,提供了较大的土体抗力。在实际边坡中,可以将边桩布置在滑体两侧稳定土体中,充分利用土体抗力,形成拱脚,承受滑坡推力。


图10 桩前土压力Fig.10 Earth pressure in front of pile
3 参数分析
3.1 模型参数
通过ABAQUS软件对边坡模型进行数值计算,分析冠梁刚度、桩位对抗滑结构内力和边坡稳定性的影响。图11为基于ABAQUS的计算模型图。抗滑桩与冠梁平面布置图如图4所示,单位为cm。各模型抗滑桩的桩长如表3所示。抗滑桩与冠梁截面均为矩形,尺寸分别为40 cm×30 cm、60 cm×60 cm。模型中土体采用单一材料,本构模型为摩尔-库伦准则中的理想弹塑性模型。桩和冠梁采用C30混凝土,采用弹性模型。模型中材料具体参数如表4所示。模型不考虑地下水、温度等因素的影响。

图11 计算模型Fig.11 Numerical model

表3 抗滑桩桩长Table 3 Pile length

表4 材料参数Tabel 4 Parameters of material
在模型建立后,计算出重力荷载下的应力和位移。然后,通过导入应力的方式进行地应力平衡。最后,在地应力平衡的基础上,在坡顶施加竖向均布荷载,荷载共分为5级,每级荷载30 kPa,共150 kPa。
3.2 冠梁刚度
冠梁在整个支护结构中起着传递荷载的作用,冠梁的刚度对桩间内力的重分布有很大的影响。在数值计算中,通过调整冠梁的弹性模量以达到改变冠梁的刚度的目的。以混凝土弹性模量E=30 GPa为基准,将弹性模量设置为0.2、1、5、10、15、20倍基准值,分析冠梁刚度对冠梁内力、桩身弯矩和桩顶位移的影响。桩间冠梁截面的轴力如图12所示。
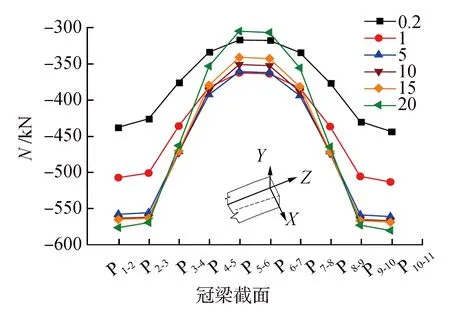
图12 冠梁轴力图Fig.12 Axial force diagram of coupling beam
由图12可知,冠梁刚度对冠梁轴力影响较大,冠梁轴力从拱顶到拱脚依次增大,说明荷载在依次向拱脚传递。冠梁刚度增大,拱脚处的冠梁轴力逐渐增大,当冠梁刚度达到5倍以上时,增辐稳定在30%左右。但拱顶处冠梁轴力在弹性模量为基准值时达到最大值364.13 kN,随冠梁刚度继续增大,此截面的轴力减小降幅最大可达16%。
冠梁刚度变化对桩身弯矩My的影响如图13所示。当不设置冠梁时,EI=0。是否设置冠梁对桩身下半部分影响较小,My沿桩长方向变化规律在桩下半部分基本一致,桩身上半部分受冠梁影响较大,My变化规律不一致,设置冠梁时桩身弯矩较大,桩身受力状态由悬臂梁变为一端固定一端简支的竖直梁,抗滑桩的支护效果更好。当冠梁刚度变大时,各桩桩顶My值变化较大,P1负弯矩值不断增大,P2~P6的桩顶弯矩由负弯矩向正弯矩变化,体现了冠梁刚度对桩的约束作用逐渐增强。P3~P6的桩顶出现正弯矩,桩体的受力状态得到进一步改善。
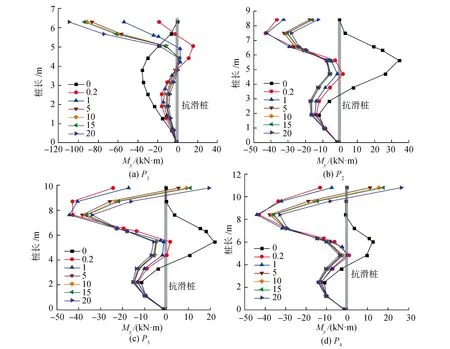
图13 MyFig.13 My
冠梁刚度不同时,桩顶位移的变化规律如图14所示。桩顶位移在随荷载增加而不断增大,两者之间的近似为线性关系。在不设置冠梁时,P1的桩顶位移较小,随着冠梁刚度的增大,U1不断增大,与不设置冠梁相比,最大增幅为50.7%。而P2~P6在设置冠梁后,桩顶受到约束,桩顶位移与不设置冠梁时相比,降幅约为16%。但随着冠梁刚度的增大,各桩的桩顶位移变化较小。设置冠梁能有效约束桩顶,但无法通过改变冠梁刚度进一步约束桩顶位移。

图14 U1Fig.14 U1
3.3 桩位
根据瑞典条分法,边坡失稳破坏时滑动面为通过坡脚的圆弧。将抗滑结构布置在不同位置,抗滑结构受力大小和支护效果不同。以坡脚为原点,沿坡面向坡顶为正方向,设置X1轴,将抗滑结构拱脚处桩布置在x1=0,2,4 m[12]处,分析桩位对桩身弯矩和边坡整体稳定性的影响,如图15所示。

图15 桩位布置图Fig.15 Diagram of pile disposition
在不同桩位处,桩身弯矩My的变化趋势如图16所示。当桩向坡顶方向移动时,桩身弯矩峰值不断增大,x1从0增大到4,P1的My增大了1.2倍。桩与滑动面交界点不断靠近桩底,My的变化规律也随着下移,且峰值不断变大。但随着桩体处于滑体处的部分越长,抗滑结构的整体稳定性下降,支护效果降低。通过强度折减法,对土的黏聚力和内摩擦角进行折减,根据折减系数FV和坡脚土体顺坡的水平位移U1曲线,判断边坡的稳定性。边坡失稳时,滑体处于无限塑性流动状态,出现很大的位移和塑性变形。根据这一特征,在有限元计算过程中,可以将滑面上节点的塑性应变或者位移出现突变作为边坡整体失稳的标志[15-16]。在x1=0,2,4 m处,边坡的FV-U1曲线如图17所示,边坡整体稳定系数分别为2.6、2.3、2.2,桩位靠近坡顶,边坡的整体稳定系数下降。P1在整个抗滑结构中,承受的荷载较大,当x1=0,P1位于稳定土体中,可利用稳定土体的支撑力,故边坡的整体稳定系数达到最大值。
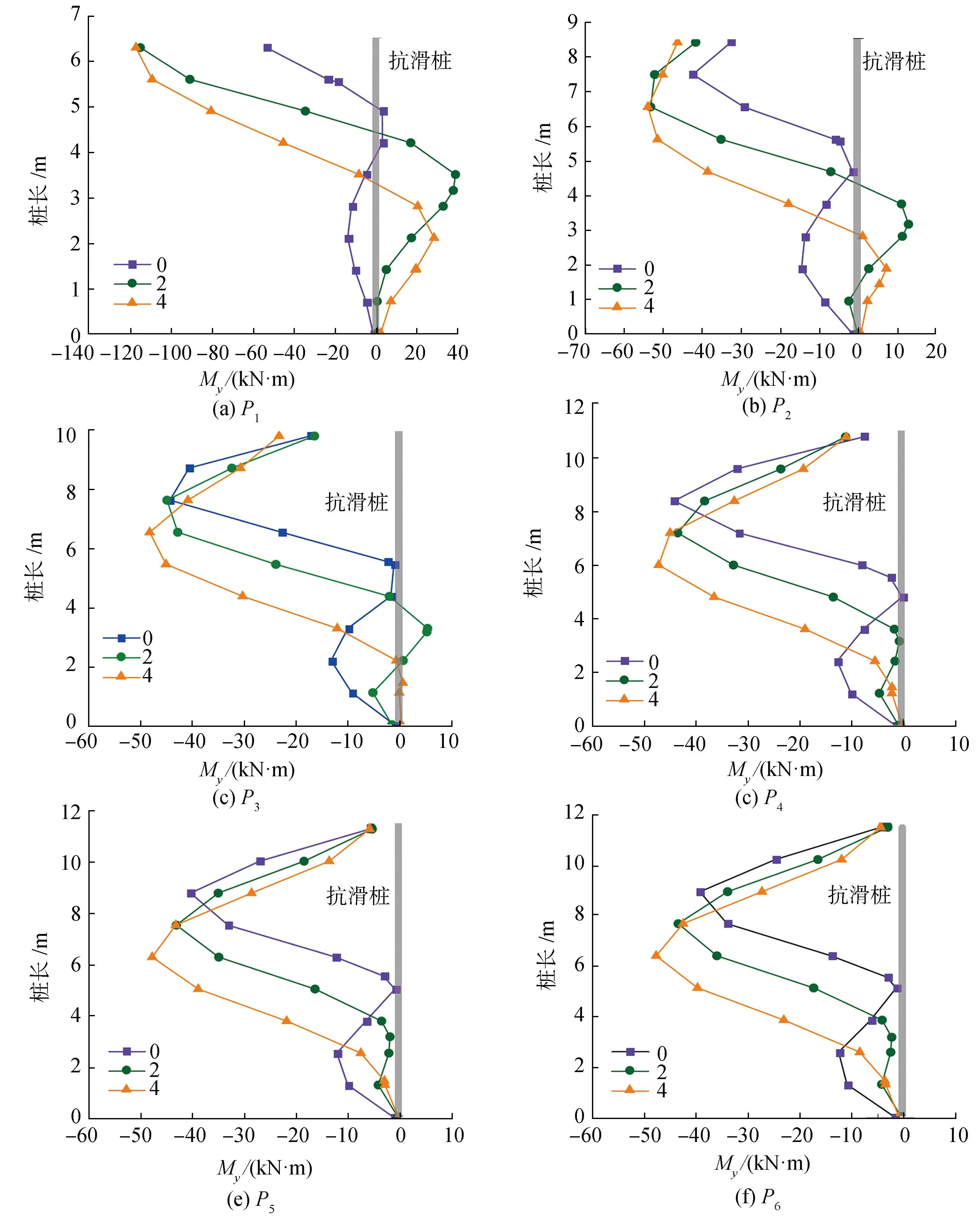
图16 MyFig.16 My

图17 FV-U1曲线Fig.17 FV-U1 diagram
4 结论
1)根据室内模型试验结果,冠梁可约束桩顶,改善桩身受力状态,对抗滑桩的受力进行重分布,并将荷载向两侧桩体逐渐传递。根据桩顶弯矩变化规律,冠梁截面的轴力为压力,从拱顶到拱脚,冠梁截面的压力不断增大。冠梁截面的受力状态有利于充分发挥混凝土的抗压性能,避免直线型冠梁中出现的剪切破坏。
2)位于坡脚稳定土体中的P1,桩前土压力随着桩身高度的增大而增大,桩顶处土体的抗力达到最大值1 425.8 Pa;而P4、P6的桩前土压力在桩顶处较小,桩体中下部的土压力较大但随桩长较小,桩前稳定土体提供了很大的支撑作用。在实际边坡中,可以将边桩布置在稳定土体中,充分利用土体抗力,形成拱脚,承受更大的滑坡推力。
3)通过计算冠梁刚度对冠梁轴力、桩身弯矩和桩顶位移的影响。是否设置冠梁只对桩身上半部分影响较大,设置冠梁时桩身弯矩较大,抗滑桩的支护效果更好。当冠梁刚度变大时,冠梁传递荷载的效应更显著,P1的My和U1均不断增大,而P2~P6的桩顶弯矩由负弯矩向正弯矩变化,部分桩体桩顶出现正弯矩,且U1减小。但随着冠梁刚度的增大,各桩的桩顶位移变化较小。设置冠梁能有效约束桩顶,通过增大冠梁刚度可以进一步改善桩体受力状态,但无法进一步约束桩顶位移。
4)当桩向坡顶方向移动时,桩身弯矩峰值不断增大,x1从0增大到4,P1的My增大了1.2倍。同时My的变化规律也随着下移。在x1=0,2,4 m处,边坡整体稳定系数分别为2.6,2.3,2.2,桩位靠近坡顶,抗滑结构的整体稳定性下降,支护效果降低。
在室内试验和数值计算中,未考虑土体的离散性和潜在滑动面,故文中结论适用于土质较均匀的边坡工程中,也可为其他类型边坡治理提供参考。
