基于改进遗传算法的磁流变阻尼器多目标空间 优化布置
2023-06-03张香成徐宏辉赵军杨洋
张香成,徐宏辉,赵军,杨洋
(1.郑州大学 力学与安全工程学院,河南 郑州 450001;2.郑州大学 水利与土木工程学院,河南 郑州 450001)
磁流变 阻尼器(Magnetorheological Damper,MRD)作为结构振动控制中最具有前景的半主动控制装置之一,因结构简单、响应迅速、阻尼力大且连续顺逆可调等特点而广泛应用于土木结构减震控制中[1-5].阻尼器对结构的减震控制效果不仅与阻尼器的数量、阻尼力大小有关,而且与阻尼器在结构中的位置密切相关,为了降低控制成本并且提高控制效率,需要对结构中的阻尼器进行优化配置.
1997 年Takewaki[6]和Wu 等[7]在结构振动控制领域引入遗传算法,并进行了大量的研究工作,至此,遗传算法在结构阻尼器优化布置中得到普遍应用.针对具体的工程优化问题,选用适当的编码和相应的遗传算子进行优化,是遗传算法的一个重要研究方向.
很多学者采用遗传算法“0-1”编码方式对阻尼器进行优化布置研究,0 表示该处不设置阻尼器,1表示设置阻尼器.贝伟明等[8]基于遗传算法采用等效二次型性能指标对MRD 进行优化布置,证明了遗传算法的有效性;閤东东等[9]采用H2范数控制理论和改进遗传算法对相邻结构间阻尼器布置位置进行优化研究,结果表明该方法可有效减小结构的二次型性能指标;孙彤等[10]基于遗传算法对轨道式负刚度装置提出一种优化布置数学模型,并以10 层钢筋混凝土(Reinforced Concrete,RC)结构为例研究了该装置优化布置基本原则;燕乐纬等[11]提出一种相对适应度函数,提高了遗传算法的进化效率;金波等[12]基于遗传算法将黏滞阻尼器替换杆件的模态应变能作为优化函数,实现了对网架结构的优化控制.“0-1”编码多将结构简化为层间剪切模型,忽略了阻尼器在结构平面和空间上分布方式的影响;对于大型空间结构,若实现精准定位则会造成“维度灾难”,计算量和计算时间难以承受.
实数编码是用具体实数表示每层阻尼器数量,郭勇等[13]采用实数编码方式将遗传算法与劣出优入算法相结合,对输电塔阻尼器的布置方式进行了多目标优化研究.数字序列编码中每个基因位数字表示楼层号,基因位数表示阻尼器个数.燕乐纬等[14]基于遗传算法提出数字序列编码,并验证了该方法的有效性;马宏伟等[15]提出粗粒度并行遗传算法,提高了优化结果收敛速度及精度.实数编码和数字序列编码大大缩短了基因维度,解决了二进制编码不能完备表达求解空间的问题,但无法实现阻尼器的精准定位.
为实现空间结构中阻尼器优化布置的精准定位,基于遗传算法提出一种新型编码方式——“AB”型数字编码,推导了MRD 附加刚度和附加阻尼矩阵,采取H2范数优化控制理论、相对适应度函数、多目标优化、代间比较权重等理论提出了改进遗传算法.采用MATLAB 软件开发了改进遗传算法MRD 多目标空间优化布置分析程序.基于文献[16-17]的建模理论,以10 层框剪偏心结构为算例验证了本文改进遗传算法的正确性和程序的有效性.
1 改进遗传算法
1.1 编码方式
为实现高层空间结构阻尼器优化布置的精确定位,对遗传算法进行合理改进,提出一种新型编码方式——“A-B”型序列编码.其中,A 对应建筑结构的楼层数,B 对应该楼层的具体位置,例如基因型为[2-1,2-4,8-7,5-3,6-10,7-5]的个体对应表现型为该结构共布置6 个阻尼器,分别布置在第二层第一个位置、第四个位置,第八层第七个位置等.假设10层结构拟布置18个阻尼器,共100个可选位置,采用遗传算法对其进行优化布置研究,4种编码方式对比如表1所示.
“A-B”型序列编码方式仅需明确定义每层可安设阻尼器位置的编号,相比于实数编码和数字序列编码可精确定位空间结构阻尼器具体安设位置,相比于“0-1”编码大大缩短基因长度,从而使得遗传算法更容易寻找最优解,加快寻优速度.
1.2 遗传操作
遗传操作包括选择、交叉、变异操作,是遗传算法的主体模块,其运算方法的设计决定了种群进化的方向.
采用轮盘赌选择方式对各个体进行优胜劣汰操作,采用单点交叉方式,对A、B 基因分开进行交叉操作,分别给予特定的交叉概率,互不影响.其中交叉位置随机生成.例如:
a1 A:3 5 4 6-8 5 6;B:6-1 9 6 3 8 7.
a2 A:3 6 6 5-4 5 8;B:6-5 9 6 3 8 1.
a1 和a2 表示两个不同基因型的个体,其中“-”表示交叉位置,完成交叉操作后得到两个全新个体为:
a1 A:3 5 4 6-4 5 8;B:6-5 9 6 3 8 1.
a2 A:3 6 6 5-8 6 5;B:6-1 9 6 3 8 7.
变异操作和交叉一致,A、B 基因互不影响,其中变异基因位、变异基因编码在允许范围内随机生成.
1.3 约束性条件及精英保留策略
相比于“0-1”编码及数字序列编码方式,“A-B”型编码方式无须考虑交叉、变异操所造成的阻尼器数量变化约束处理问题,但会出现基因重复现象,即在交叉、变异过程中有可能出现两个基因位基因代码相同的情况.基于“A-B”型编码方式的特点,提出一种基因代码转换方式,将个体各基因位代码转换为十进制数字,每个数字在交叉、变异过程中进行甄别,若出现相同数字则对其进行“变异”操作,直至无重复数字为止.
在每代的选择、交叉、变异操作之后,将当代种群中最小适应度值与上述操作前最大适应度值进行对比,保留适应度值高的个体进入下一代,即“末尾淘汰、精英保留”.随着种群的不断迭代,种群整体适应度值不断提高,即基因优良性不断提高.
2 优化控制理论
2.1 优化目标函数
采用H2范数优化控制理论对MRD 进行优化布置研究,MRD受控结构减震运动微分方程如下:
式中:M、C、K分别是结构的总质量矩阵、阻尼矩阵、总刚度矩阵;分别为受控框剪结构的加速度、速度、位移响应;为施加在结构上的地震波加速度;R是地震作用列向量;H是MRD 的位置矩阵;F(t)是MRD 所提供的控制力向量.阻尼矩阵C采用Rayleigh正交阻尼模型,详见文献[16].
对阻尼力进行变形重组,可得等效刚度和等效阻尼,如下:
结合公式(1)、(2)可得:
式中:=C+HG2为结构的总阻尼矩阵;=K+HG1为结构的总刚度矩阵.
式(3)的状态空间的状态函数为:
对受控系统状态方程进行拉普拉斯变换,并求取其传递函数:
式中:s为拉普拉斯算子[18].
传递函数的H2范数可用式(6)计算:
式中:Lc为Lyapunov 方程ALc+LcAΤ=-BBΤ的非负定解.
2.2 多目标优化与代间比较权重
多目标优化最优解称为Pareto 最优解,其特点是随着优化进程各目标函数齐头并进,且在无法提升任何目标函数的同时保证不削弱任何目标函数.多目标优化算法以MRD 受控结构层间位移的H2范数指标和加速度的H2范数指标联合控制对MRD 布置位置进行优化计算,优化目标函数如式(7)所示.
代间比较权重定义如下:
枣棉间作条件下,不同灌水量对棉花产量存在显著影响(图3),适量供水和轻度水分胁迫下产量表现较好,充分供水次之,中度水分胁迫产量最低。M3W3处理产量较M3W1、M3W4分别高62. 5%和13. 9%,M3W2处理产量较M3W1、M3W4分别高55. 6%和9. 0%,M3W4处理产量较M3W1高42. 7%,M3W3处理产量与M3W2处理无显著差异。
代间比较权重使得进步慢的目标函数将获得较大的权值,以促进各目标函数间的均衡发展.相比于人为定义权重值以及适应性权重的方法,其不仅排除了人为因素定义两个权重值不同造成的影响,而且提供了种群向最优目标进化的方向和搜索压力,同时又使得这种压力在各指标间均匀地进行分配.
2.3 适应度函数
适应度函数值的大小影响着个体被遗传到下一代的概率,个体适应度函数值越大,遗传到下一代的概率越高.为实现目标函数到适应度函数的良性映射,提高优良个体遗传到下一代的概率,采用相对适应度函数进行遗传操作.
式中:为相对适应度函数;f(xi)为个体目标函数;{f(x)}为当代种群目标函数集合.
2.4 程序编制
基于MRD 受控结构三维计算模型、经典遗传算法、“A-B”型编码方式、H2范数优化控制理论、多目标优化与代间比较权重等理论,采用MATLAB 软件开发了改进遗传算法阻尼器空间位置寻优程序.程序计算流程如图1所示.
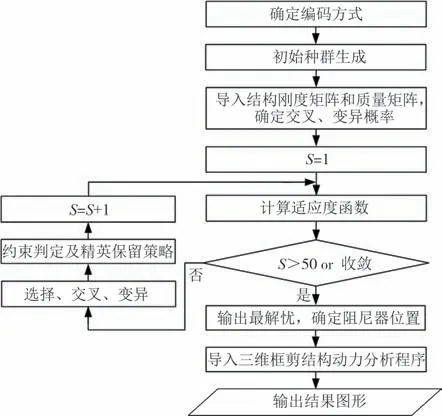
图1 改进遗传算法阻尼器空间位置寻优程序流程图Fig.1 The flow chart of the optimization procedure for the spatial position of the damper in the improved genetic algorithm
3 优化模型及地震波选取
3.1 优化模型
以10 层RC 框剪结构为例,结构的混凝土强度等级为C35,弹性模量为3.25×104MPa,泊松比为0.2,钢筋混凝土密度为2 500 kg/m3,楼板厚度为0.12 m,剪力墙厚度为0.20 m.结构的三维模型如图2 所示,一至三层框架柱的截面尺寸为0.7 m×0.7 m,四层及以上框架柱的截面尺寸为0.6 m×0.6 m;跨度为9 m梁的截面尺寸为0.3 m×0.7 m,跨度为4.5 m 梁的截面尺寸为0.25 m×0.5 m,跨度为6.3 m 和6.0 m 梁的截面尺寸为0.25 m×0.6 m.RC 框剪结构的前两阶振型阻尼比假定为0.05,并将底层柱下端视为固结.图2 中数字为节点编号值及阻尼器位置编号.建模理论、程序中所采用的MRD 及其在结构中的设置方式和文献[17]中一致,此处不赘述.
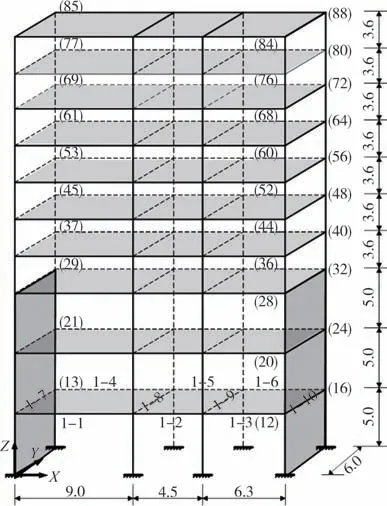
图2 三维框剪偏心模型(单位:m)Fig.2 3D frame shear eccentric model(unit:m)
3.2 地震波选取
根据《建筑抗震设计规范》(GB 50011—2010)[19],拟建场地建筑抗震设防烈度为7(0.1g)度、Ⅲ类场地、设计地震分组为第一组,地震动加速度反应谱特征周期为0.45 s,水平地震影响系数为0.5.根据场地类别和设计地震分组,选取ATC-63 FEMA P-695 规范[20]推荐的22条远场地震记录中的5条水平分量作为时程分析的实震输入,另外选取2 条人工波作为补充,将7 条地震波加速度时程最大值均设置为220 gal,分别绘制加速度响应谱曲线、平均谱曲线与设计谱曲线,如图3所示.与设计反应谱相比,7组地震波平均反应谱在结构主周期点上误差为6.48%(设计反应谱:0.209 3,平均反应谱:0.223 8),满足误差不超过20%的规范要求.
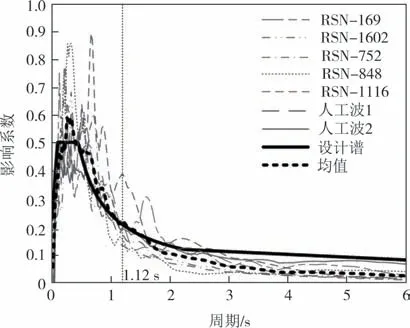
图3 输入地震波各时程谱及平均谱与设计谱对比Fig.3 Comparison of each time-history spectrum and average spectrum of the input seismic wave with the design spectrum
4 优化方案验证
结构共100 个可选位置(每层10 个),拟设18 个MRD.经过程序试算,初始种群大小设为300,交叉概率设置为0.6,A、B 变异概率均设置为0.1,程序可迅速得出最优解.程序设置为连续进化20 代适应度函数值不发生改变或者进化到50 代时程序自动停止搜索.对于超大型建筑结构可参照文献[15],能提高寻优速度和最终优化结果的准确度.
4.1 位置优化结果
程序运行235 min 计算完毕,多目标优化进程如图4 所示.图4(a)~(c)分别为以层间位移为输出的H2范数指标、以加速度为输出的H2范数指标和以多目标评价函数随进化代数的变化.从图4(c)中可以看出多目标评价函数指标随着进化进程前期迅速增大,中期缓慢上升,后期趋于稳定.为验证优化结果的正确性,对4 种工况进行对比,即:工况一,不设置MRD;工况二,随机布置;工况三,底层均匀布置;工况四,优化布置方案.优化方案中X向MRD共12个,Y向6 个,为排除各工况X、Y向阻尼器数量不同的影响,工况二、工况三中X、Y向阻尼器数量调整为12个、6 个,并分别计算各工况下以层间位移为输出结构的H2范数指标值H2d和以加速度为输出结构的H2范数指标值H2a,如表2所示.
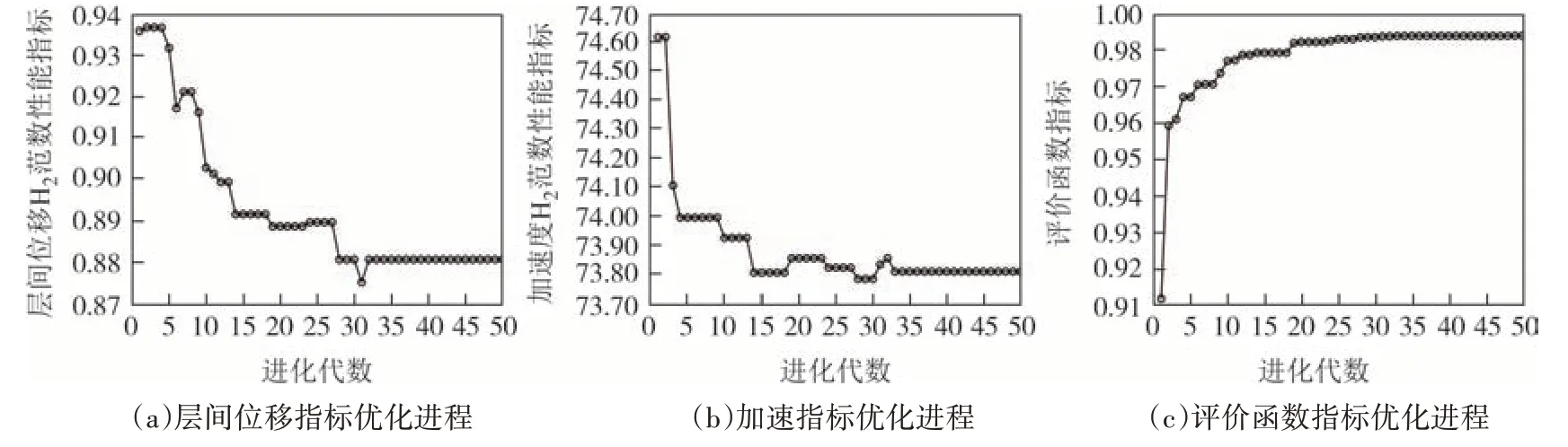
图4 改进遗传算法多目标优化进程Fig.4 Improved genetic algorithm multi-objective optimization process
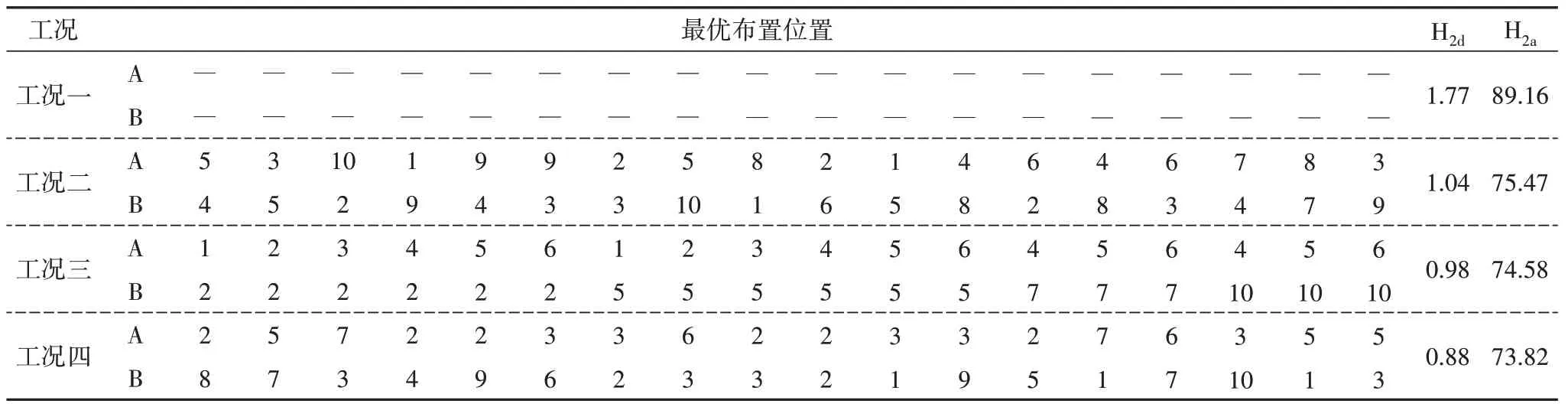
表2 各工况MRD布置位置及H2范数值Tab.2 MRD layout position and H2 norm value of each scheme
4.2 时程响应对比
为了更为明显地对比4种工况下MRD对结构的减震控制效果,以顶层88 号节点为例,7 条地震波激励下的水平双向位移时程响应分别取前30 s 进行绘制(RSN-848 地震波总时长28 s,取全程),并分别在位移峰值处局部放大,如图5 所示.从图5 中可以明显地看出,无论是在哪一条地震波激励下,工况二、工况三、工况四对应结构顶层88 号节点的X、Y向位移均明显小于工况一条件下对应时间点下的位移响应,说明在地震波激励下MRD 可明显减小结构的位移响应.工况二、工况三、工况四在7 条地震波激励下结构顶层88号节点X向最大位移的平均减震率分别为31.97%、34.81%、39.45%,Y向最大位移的平均减震率分别为22.93%、29.95%、32.68%.该结果与表2各工况范数指标值相对应,说明了基于范数优化控制理论的改进遗传算法空间位置寻优程序的有效性,实现了对阻尼器最佳布置位置的精确定位.

图5 7条地震波激励下结构顶层88号节点水平双向位移时程响应Fig.5 Time history response of horizontal bidirectional displacement of No.88 node on the top floor of the structure under the excitation of seven seismic waves
4.3 各层最大位移、加速度对比
图6 为7 条地震波作用下框剪结构各层水平双向位移、加速度平均值包络图.由图6 可知,MRD 受控结构各层最大位移、最大加速度响应均小于未控结构.其中,工况四X向各层位移明显小于工况二、工况三,Y向略小于工况二、工况三.以中间楼层 第五层为例,7条地震波激励下工况一至工况四X向平均位移分别为54.52 mm、36.84 mm、36.12 mm、34.88 mm,相比于工况一,工况二、工况三、工况四分别减少了32.43%、33.75、36.05%;Y向平均位移分别为23.18 mm、18.34 mm、15.18 mm、14.96 mm,相比于工况一,工况二、工况三、工况四分别减少了20.88%、34.51%、35.46%.Y向一至三层位移略小于其他各层,原因是该结构一至三层在Y向布置了剪力墙,该位置自身刚度足够大,抗剪能力足够强.
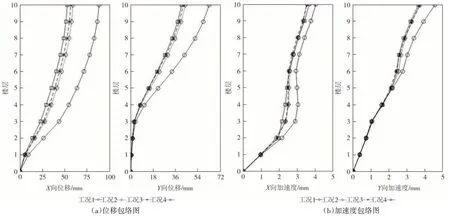
图6 框剪结构各层水平双向位移、加速度包络图Fig.6 Horizontal bidirectional displacement and acceleration envelopes of each layer of frame-shear structure
在地震波激励下,结构刚度和阻尼的增加均会减小位移响应,对于加速度而言,虽然阻尼的增加会减小结构的加速度响应,但刚度的增加会加大结构加速度响应.因此,MRD 受控结构的加速度减震效果不如位移减震效果明显,甚至在某些时刻加速度会出现增大的现象.因结构加速度响应结果的复杂性,单层加速度对比有大有小,故采用式(10)对工况二、工况三、工况四的加速度响应进行综合评价.
式 中:J1为加速 度指 标;n为 楼层 数;aixmax、aiymax、aix0max、aiy0max分别为X、Y向受控和未控状态下各层各节点最大加速度均值.
经过计算,工况二、三、四加速度综合指标值J1分别为1.794、1.778、1.771,说明3 种工况相比,工况四的加速度综合减震率最大,工况三次之,工况二相对最小.
4.4 结构扭转控制
7 条地震波激励下结构各层水平双向最大位移对比如表3所示.从表3可看出工况二、工况三、工况四与工况一相比,X向扭转略有增加但不明显,其中工况四各层位移比值更接近于1;Y向工况二扭转加剧,工况三、工况四明显减小,其中工况四各层位移比值更接近于1,最大位移比值顶层1.064,远远小于工况一顶层最大位移比值1.314.对比分析结果表明:MRD 布置位置不当会加剧结构的扭转响应;空间位置寻优算法计算结果对结构的扭转控制作用显著.
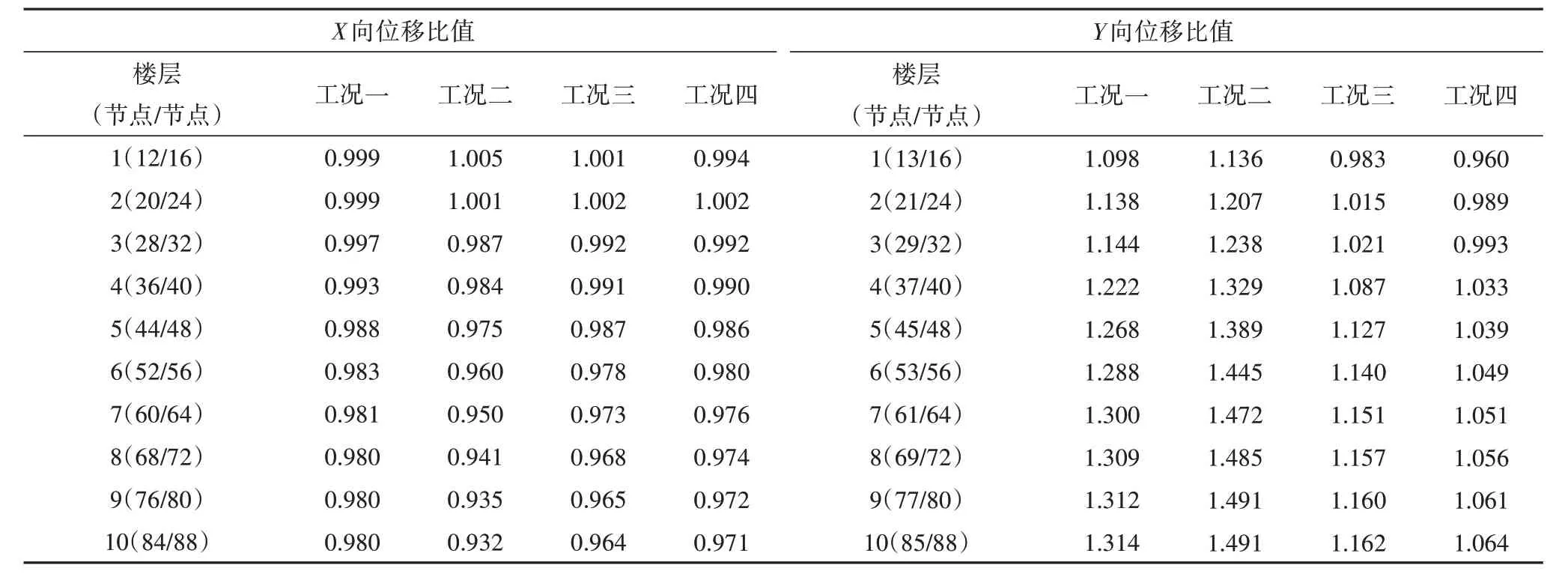
表3 7条地震波作用下各层水平双向最大位移比平均值Tab.3 The average value of the horizontal bidirectional maximum displacement ratio of each layer under the action of seven seismic waves
4.5 数量优化研究
基于结构安全性和设置MRD 带来的经济支出,本节对安设MRD 数量与结构减震性能的关系进行分析.提出3种评价指标,分别为加速度指标J1、层间位移角指标J2、综合评价指标J3,从多角度综合分析不同数量的阻尼器对结构整体的减震控制效果.
式中:θixmax、θiymax、θix0max、θiy0max分别为X、Y向受控和未控状态下各层各节点最大层间位移角均值.
为充分说明不同数量的阻尼器对结构综合减震率的影响,基于MRD 受控框剪结构三维框剪计算模型和改进遗传算法,对该结构不同数量的阻尼器布置位置进行优化.优化程序参数设置和上文一致,分别计算设置12、16、20、24、28、32、36 个阻尼器的最优分布位置,并计算在7 条地震波激励下各工况以及满置下结构的综合评价指标,并取其平均值绘制阻尼器数量对应综合评价指标影响关系曲线,如图7所示.从图7 中可看出:J1与J2相比,J2即层间位移角指标值较小,说明MRD 对结构的位移减震效果强于加速度的减震效果;3 种评价指标均随着MRD 数量的增多总体上逐渐减小,减小幅值趋于平缓,说明随着结构中MRD 的不断增加,结构的层间位移角、加速度减震率虽逐渐增大,但减震性价比逐渐减小;通过对比3 种评价指标走势发现,当MRD 数量超过18时,3 种指标下降率均趋于平缓,在不考虑其他因素的情况下,说明该结构设置18个MRD减震控制效果最佳.
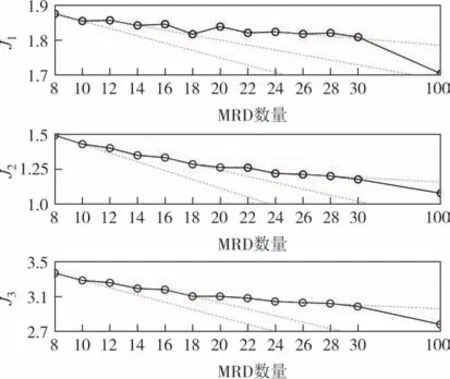
图7 各减震评价指标随MRD数量变化趋势图Fig.7 Trend chart of each shock absorption evaluation index with the number of MRDs
4.6 阻尼器耗能分析
图8 为RSN-1116 地震波作用 下X向2~4 号和Y向6~7号MRD 的阻尼力-位移滞回曲线.从图8中可以看出,在地震波的作用下,MRD 的滞回环呈椭圆形,且阻尼力幅值随位移幅值的增大而增大,说明MRD 能够稳定地耗能;此外,位移和阻尼力不会在同一时刻达到最大值.当滞回环中位移幅值小于 2 mm 时,MRD 的阻尼力为10 kN;当滞回环的位移幅值大于 14 mm 时,滞回环中MRD 的阻尼力最大可以达到200 kN.
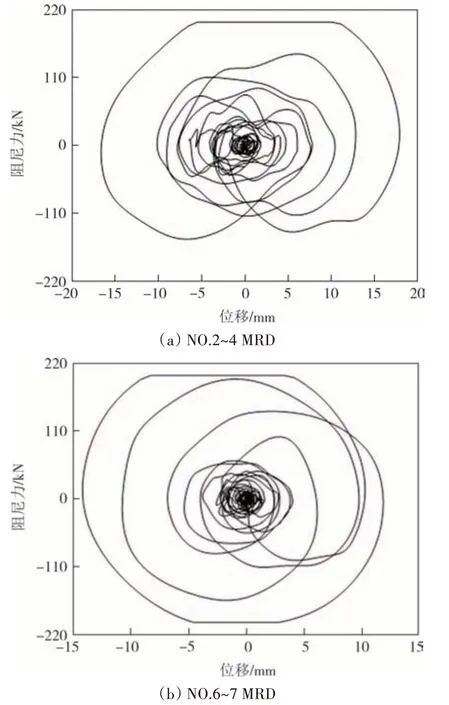
图8 RSN-1116波作用下MRD的阻尼力-位移滞回曲线Fig.8 Damping force-displacement hysteresis curve of MRD under the action of RSN-1116 wave
5 结论
1)基于遗传算法提出了“A-B”型数字编码,推导了MRD 附加刚度和附加阻尼矩阵,采用H2范数优化控制、代间比较权重等理论提出了改进遗传算法,并开发了MATLAB 程序,实现了对空间结构中MRD的精确定位和多目标优化布置.
2)基于MRD 受控RC 结构三维计算模型程序,采用该算法对10 层框剪结构MRD 的布置进行优化研究,结果表明:改进遗传算法优化结果迅速收敛;4种工况中优化方案控制效果最佳,顶层88号节点X、Y向减震率分别达39.45%、32.68%,结构扭转得到有效控制.
3)对不同数量MRD 优化布置进行分析,结果表明其综合减震指标虽然随着数量的增加而减小,但降低趋势也逐渐减小,该指标可为阻尼器的数量优化提供依据.
4)MRD 的滞回环呈椭圆形,且阻尼力幅值随位移幅值的增大而增大,说明MRD 能够稳定地发挥耗能作用.
