基于类平衡矩阵的桁架构件重要性计算方法

周雅，王方，蔡建国，冯健

［混凝土及预应力混凝土结构教育部重点实验室（东南大学），江苏 南京210096］

近年来，突发事件引起的结构连续性倒塌问题已受到国内外的广泛关注.偶然荷载下建筑结构的连续性倒塌会对生命、财产安全造成极其巨大的伤害和损失，而此时增强结构抵抗局部破坏持续引发其他构件连续性破坏的能力即鲁棒性，则往往比直接抵抗偶然荷载更有效和实用［1］.国内外学者对鲁棒性的定义仍有较大争议［2］，但总体上鲁棒性反映了结构对局部破坏的不敏感性.对鲁棒性理论进行研究是提高结构抗连续性倒塌性能的基础.目前国内外针对结构鲁棒性的定量分析主要从两个方面出发：结构属性及结构性能［3］.前者涉及结构体系拓扑和刚度分布，后者主要基于结构承载力与变形.如Blockley 等［4］通过分析不同初始破坏对结构系统的影响，识别其薄弱环节，提出了结构脆弱性评价理论；Jiang 等［5］提出判断关键杆件的方法以及基于线性静态分析程序的安全评估方法；叶列平等［6］通过理论推导定义了考虑荷载作用的广义结构刚度以进行构件重要性计算；黄靓等［7］从结构承载力出发建立了鲁棒性量化方法；陈永亮等［8］基于抗力利用率，提出了构件易损性系数量化方法；霍静思等［9］定义节点延性系数，提出了采用该系数评估连续倒塌过程中节点延性的方法；Tavakoli 等［10］针对框架结构体系，提出基于能量理论的鲁棒性指标.目前鲁棒性理论已应用于各类框架结构［10-12］、空间网格［13-15］等结构体系的设计计算中.

对于简单结构如桁架结构体系，采用基于结构属性的鲁棒性指标具有简洁清晰、计算方便的优势，虽然无法考虑弹塑性动力效应的影响，但仍广泛应用于空间结构中.构件重要性系数能体现突发事件下单一构件破坏对整体结构性能的影响程度，因此一些学者建议采用构件重要性系数作为评价鲁棒性的指标［3］.如Nafday［16］通过比较拆除单一构件后剩余结构的刚度矩阵行列式与原始结构的整体刚度矩阵行列式，判别此构件失效对结构整体刚度的影响；蔡建国等［17-19］通过基于概念判断的敏感性分析方法对网架结构进行重要构件评估，并利用刚度矩阵的特征值分析空间桁架结构的构件重要性.另外，数值方法也常应用于构件重要性判断，如Brunesi 等［20］将有限元方法与数值方法相结合，模拟柱构件拆除后的结构损伤机制.目前，关于构件重要性系数的计算方法较多，可基于结构刚度矩阵［6］，也可引入结构承载力系数［21］或结构内力转化矩阵［22］等.如朱南海等［23］建立了构件冗余度及其易损性评价指标，并将构件的重要性指标定义为构件易损性系数与冗余度系数的比值；蒋淑慧等［24］利用剩余结构冗余度分布系数，定量分析杆系结构中的构件重要性；张立森等［25］将构件内力分项计算值与抗力分项值之比定义为构件重要性系数，以体现构件抗力的利用水平.

现有研究中，基于刚度的重要构件判断方法主要采用初始刚度或变形后的材料刚度，适用于一般的框架结构.然而，空间网格结构跨度较大、杆件数目较多且具有几何非线性特征，材料刚度与几何刚度的计算过程较为复杂.为了简化计算过程、提高计算效率，在基于刚度的重要构件判断方法基础上，选取刚度矩阵行列式作为结构的响应.在假设各桁架杆件线刚度近似相等、不考虑结构应力刚化作用或应力刚化所贡献的刚度很小的前提下，通过数学推导，将基于刚度的重要构件判断方法简化为基于类平衡矩阵的重要构件判断方法，并进行算例分析验证.

1 类平衡矩阵

假定结构体系中任一自由节点k分别与其他N个节点（编号为k1，…，kN）连接，形成某铰接杆件体系（图1）.当该结构体系处于平衡状态时，自由节点k处各杆件的内力与外力互相平衡.将杆件内力作为基本未知量，建立节点平衡方程为：

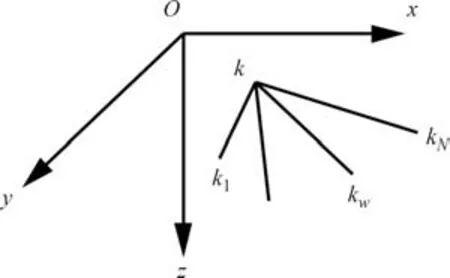
图1 节点连接示意Fig.1 Connecting joint diagram

式中：xk、yk、zk为节点k在整体坐标系中的三向坐标值；xkw、ykw、zkw为其他N个节点中任一节点kw在整体坐标系中的三向坐标值；Lkkw为连接节点k、kw的杆件长度；Fkkw为连接节点k、kw的杆件实际内力；Fkx、Fky、Fkz分别为节点k的外力在x、y、z方向上的分量.

进行规整化处理时采用力密度代替实际内力.连接节点k、kw的杆件力密度可表示为：

对于整个结构体系，可以依次对每一个自由节点建立如式（1）所示的平衡方程，集成整合后的整体平衡方程为：

平衡矩阵的组成元素包含了结构体系的节点坐标信息和节点连接关系.矩阵行元素为各杆件内力在节点某一自由度上的分量系数，矩阵列元素为某杆件内力在各节点自由度上的分量系数.

对节点平衡方程重新进行规整化处理，将杆件实际内力作为未知量，把杆件长度融入平衡矩阵中，则平衡方程可改写为：

式中：F为杆件内力向量；A为类平衡矩阵，维数为dn×m；L-1为由杆件长度倒数组成的对角矩阵.

2 构件重要性系数与类平衡矩阵的关系

对于某铰接杆件体系，若不考虑应力刚化的影响或应力刚度所贡献的刚度很小，则切线刚度矩阵表达式可以简化为：

式中：G为由杆件线刚度组成的对角矩阵，维数为m×m；Q为由力密度向量组成的对角矩阵.由此可见，切线刚度矩阵可以转化为材料刚度矩阵.

令li、ei、ai分别为结构体系中任一杆件i的长度、弹性模量和截面面积.若结构体系中各杆件的线刚度都相等，即eiai/li=g，则其线刚度矩阵可表示为G=gI，其中g为杆件的线刚度，I为m×m的单位矩阵.切线刚度矩阵可简化为：

基于杆件敏感性分析，将无荷载作用下结构体系中杆件i的重要性系数αi定义为：

式中：γ0为正常情况下结构的初始响应；γi为杆件i失效后结构的响应.

将简化后的刚度矩阵（6）代入式（7）中可得：

式中：K0、A0分别为完整结构的刚度矩阵与类平衡矩阵；Ki、Ai分别为杆件i失效后的结构刚度矩阵与类平衡矩阵.由此可知，当铰接杆件体系的各杆件线刚度相等、不考虑结构应力刚化作用或应力刚化所贡献的刚度很小时，构件重要性系数只与类平衡矩阵有关.

3 类平衡矩阵的奇异值分解

矩阵奇异值分解是矩阵对角化分解的一种类型，广泛应用于最优化问题、系统理论和控制及图像处理等领域中.对于某矩阵B∈Rs×t，矩阵的秩为r，矩阵B的奇异值为t阶方阵BTB（或s阶方阵BBT）的正特征值的平方根，在Matlab 软件中可通过［USV］=svd（B）对B进行如下形式的奇异值分解：

式中：U和V为2 个相互正交矩阵，分别为左奇异矩阵和右奇异矩阵；Λ=diag（σ1，σ2，···，σr，），其中为奇异值，λp为方阵BTB的特征值，且p∈［1，r］.

当结构体系处于平衡临界状态时，结构刚度矩阵的最小特征值为0.当最小特征值小于0 时，表明结构无法维持平衡.因此，一般情况下，结构的刚度矩阵特征值均大于0.由此可知，对于第1 节中处于平衡状态的自由节点总数为n的结构体系，刚度矩阵K∈Rdn×dn的秩r=dn，为满秩矩阵.刚度矩阵的特征值列向量可表示为：

若结构中各杆件的线刚度均相等，则根据式（6）可知，方阵AAT∈Rdn×dn的特征值列向量为：

式中：杆件的线刚度g＞0.

如果某铰接体系具有足够的外部约束，基于Maxwell 准则进行几何稳定性分析时，其静定、动定的必要条件为：

若体系满足式（12），则其平衡方程数与未知量数相等，方程组有唯一解，即结构存在唯一的内力态和变形态.

依照Maxwell 准则，一般情况下，铰接体系满足条件m≥dn，因此矩阵A的秩r≤dn，即其奇异值阶数小于或等于dn.根据矩阵奇异值分解的数学定义，类平衡矩阵A∈Rdn×m的奇异值σq是方阵AAT正特征值的平方根，则由矩阵A奇异值组成的列向量为：

式中：σiq、σq分别为杆件i失效后及失效前类平衡矩阵A的第q个奇异值.由式（15）可知，提出的构件重要性系数可以直接利用类平衡矩阵A的奇异值进行计算，而无须集成整体刚度矩阵，故可简化步骤，提高计算效率.

若将构件i的重要性系数重新定义，将响应更改为类平衡矩阵A的奇异值乘积，则构件i的重要性系数为：

综上所述，在假设条件下，可根据式（15）计算基于刚度的构件重要性系数αi，修正结构响应的表达后，可根据式（16）计算基于类平衡矩阵的构件重要性系数αiA.比较式（15）与式（16），虽然两者计算的重要性系数值不同，前者稍大于后者，但构件在整体结构上的重要性排序一致.因此，可以采用式（16）来判断构件在整体结构中的重要性.

4 算例分析

算例1 为如图2 所示的某二维桁架结构.图中，N1～N4为该桁架的节点，M1～M6为该桁架的杆件单元，该桁架结构的自由节点数为2，满足Maxwell准则，因此刚度矩阵的特征值阶数为2×2=4.为简化说明，参数均采用无量纲.假定杆件M3、M4的截面刚度为1.414，杆件M1、M2、M5、M6的截面刚度为1，长度均为1，则各杆件的线刚度均为1.算例1 中完整结构体系的刚度矩阵特征值和类平衡矩阵的奇异值见表1.根据式（15）和（16）计算得到的构件重要性系数见表2.表2 中αi与αiA为该桁架结构中杆件i分别基于刚度及类平衡矩阵的构件重要性系数.

表1 算例1的特征值与奇异值计算结果Tab.1 Eigenvalues and singular values of example 1

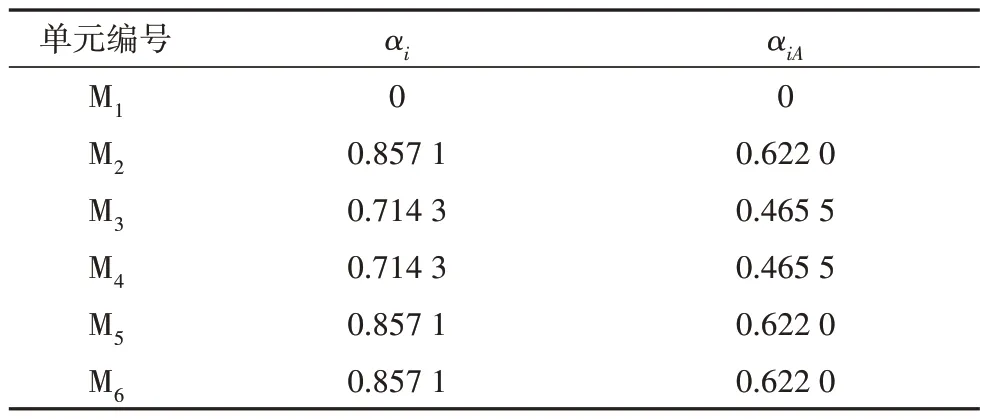
表2 算例1的构件重要性系数计算结果Tab.2 Calculated component importance coefficients of example 1

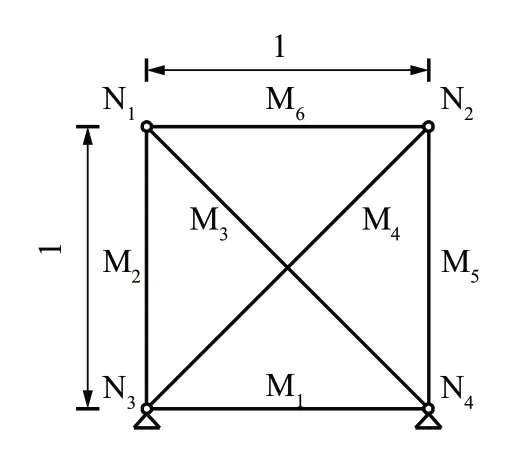
图2 算例1的桁架体系示意图Fig.2 Schematic diagram of truss system of example 1

由表1 可知，刚度矩阵特征值与类平衡矩阵奇异值的平方呈线性关系，结果与式（14）一致.由表2可知，算例1 中M2、M5、M6为最重要的杆件，M3、M4杆件次之，M1杆件最不重要.虽然基于类平衡矩阵的构件重要性系数αiA小于基于刚度的构件重要性系数αi，但两种重要性构件判断方法的计算结果一致.

算例2 为3 个相同网格单元组成的某二维桁架结构，如图3 所示.图中，P1～P8为该桁架的节点，E1～E16为该桁架的杆件单元，其中自由节点数为6，满足Maxwell准则，因此刚度矩阵的特征值阶数为2×6=12.为计算方便，采用无量纲参量表示截面刚度与几何参数，假设单网格的跨度和高度均为1，杆件的线刚度均为1.分别计算算例2 完整结构体系的刚度矩阵特征值和类平衡矩阵的奇异值，结果见表3.分别按照式（15）和式（16）计算构件的重要性系数，利用结构体系的对称性，可只计算左半侧的杆件，结果见表4.

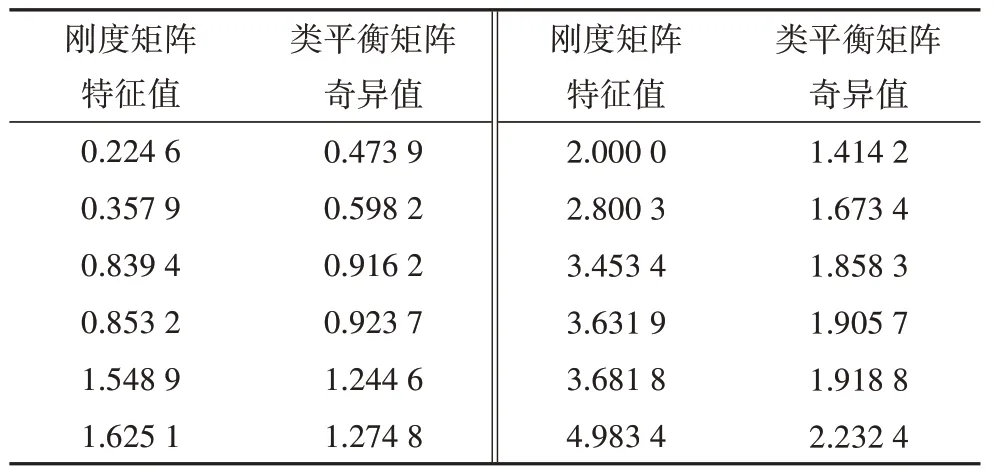
表3 算例2的特征值与奇异值计算结果Tab.3 Eigenvalues and singular values of example 2

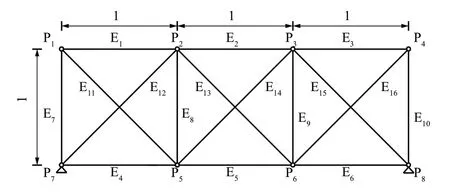
图3 算例2的桁架体系示意图Fig.3 Schematic diagram of truss system of example 2

由表3 可知，刚度矩阵特征值与类平衡矩阵奇异值的数学关系与式（14）一致，特征值与奇异值的平方成正比，因此在计算重要性系数时可以直接代入类平衡矩阵的奇异值.由表4 可知，算例2 半结构中E1、E7为最重要的杆件，E5为最不重要杆件.同算例1，基于类平衡矩阵的构件重要性系数αiA小于基于刚度的构件重要性系数αi.虽然两种重要性构件判断方法采用的结构响应不同，但基于类平衡矩阵与基于刚度的重要构件判断方法计算结果一致.

算例3 为如图4 所示的一三维桁架结构.其中，J1～J12为节点，H1～H31为杆件单元，其中自由节点数为8，因此刚度矩阵的特征值阶数为3×8=24.参数均采用无量纲，则各杆件的线刚度均为1，底部共有4 个约束点.计算三维算例3 刚度矩阵特征值和类平衡矩阵的奇异值，见表5.利用结构体系的对称性，半结构构件的重要性系数见表6.

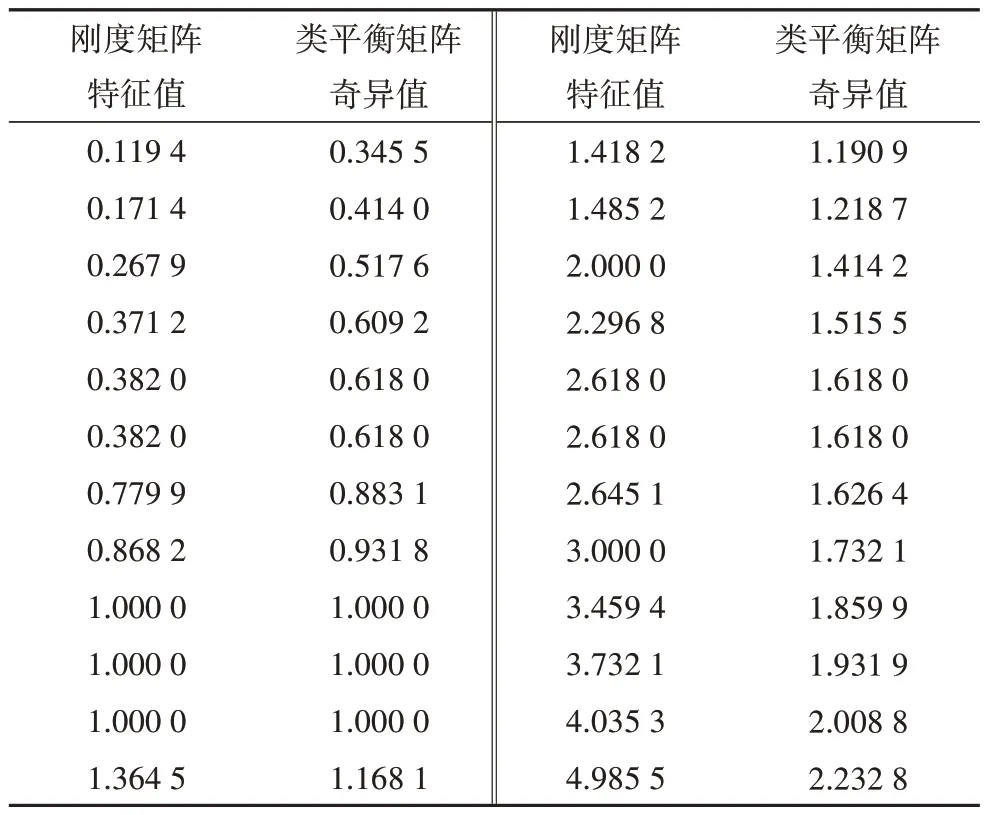
表5 算例3的特征值与奇异值计算结果Tab.5 Eigenvalue and singular values of example 3

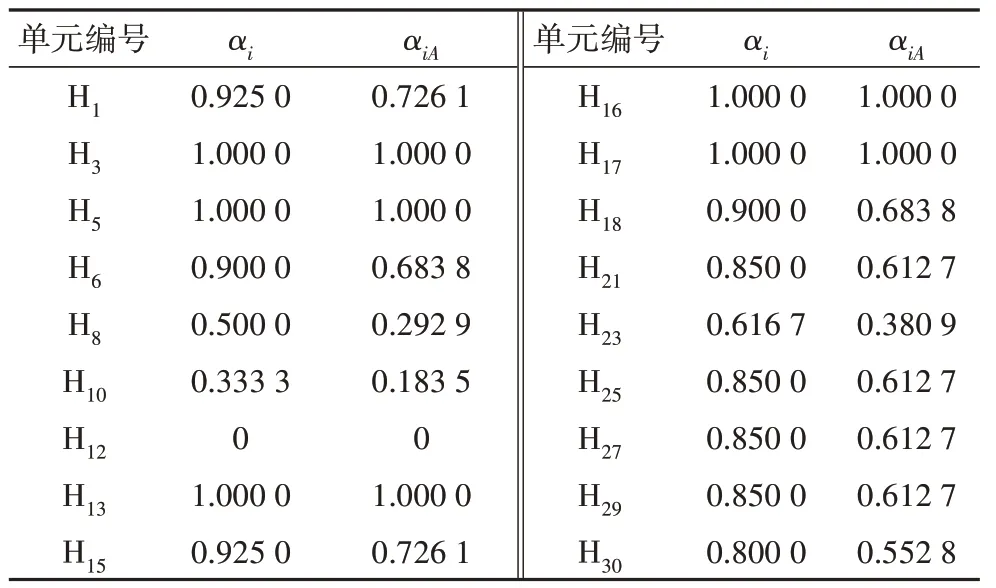
表6 算例3的构件重要性系数计算结果Tab.6 Calculated component importance coefficients of example 3

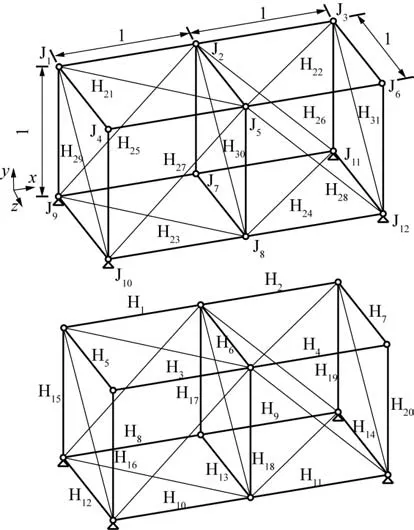
图4 算例3的桁架体系示意图Fig.4 Schematic diagram of truss system of example 3

表5 中刚度矩阵特征值与类平衡矩阵奇异值的关系与算例1、2 相同.由表6 可知，算例3 半结构中H3、H5、H13、H16、H17同为最重要的杆件.H12重要性系数最小，为0，因其连接在两个约束之间，属于不受力构件，证明了重要性系数计算的正确性.基于类平衡矩阵的构件重要性系数αiA总体上小于基于刚度的构件重要性系数αi.基于数值排序，其重要构件判断方法计算结果一致.

根据以上3 个典型算例的分析结果可知，当不考虑结构应力刚化作用或应力刚化所贡献的刚度很小且各杆件线刚度相同时，可采用以类平衡矩阵奇异值乘积为响应的重要性系数来判断铰接杆件体系的构件重要性.

5 结论

1）当铰接杆件体系的各杆件线刚度近似相等，且不考虑结构应力刚化作用或应力刚化所贡献的刚度很小时，构件重要性系数只与类平衡矩阵有关.

2）对类平衡矩阵进行奇异值分解，建立刚度矩阵特征值与类平衡矩阵奇异值的数学关系式.以类平衡矩阵奇异值乘积为响应，提出了一种基于类平衡矩阵的重要性构件判断方法.

3）算例分析结果表明，基于类平衡矩阵的重要构件判断方法与基于刚度的重要性构件判断方法计算结果一致.

4）基于类平衡矩阵的重要构件判断方法是一种切实可行的空间结构重要构件快速计算方法.