RSA型基于证书签名方案

郭亚峰, 黄 慧, 陈红英

(1.漳州城市职业学院 电子信息工程系,福建 漳州 363000; 2.闽南师范大学 计算机学院,福建 漳州 363000)

密码学家Gentry[1]在2003年欧密会上首次提出基于证书公钥密码(certificate-based public key cryptog-raphy,CB-PKC)的概念.在CB-PKC系统中,公钥的证书直接被用作解密或签名密钥的一部分,解决了传统公钥基础设施(public key infrastructure, PKI)证书管理问题;另一方面,由于证书只是密钥的一部分,还有另一部分密钥只有用户才知道,也解决了基于身份公钥密码[2](identity-based cryptography, IBC)的密钥托管问题,证书的分发也不需要保密信道.2004年Kang等[3]将基于证书概念平移到数字签名,研究基于证书签名(certificate-based signature,CBS), 文献[3]给出CBS的安全模型和第一个可证明安全的CBS方案.Wu等[4]对CBS与无证书签名方案[5](certificateless signature,CLS)之间的关系进行了研究,提出一种从CLS到CBS的通用转换方法,并证明该方案是安全的.2012年Li等[6]提出只有一个群元素的短CBS,其方案的签名只是一个群元素,但方案在签名过程、验证过程都需要3个双线对运算,效率并不高.为了提高CBS签名方案的效率.Hung等[7]基于CDH假设提出了一种短CBS方案,然而,Kumar等[8]指出Hung等[7]方案不能抵抗无证书用户的攻击.Lu等[9]提出了一种改进的不需要随机预言机假设的CBS方案.在标准模型下,Zhou等[10]与Wang等[11]分别提出了基于双线性对的CBS方案.基于格和短整数解(SIS)假设,Tseng等[12]提出了一个新的高效CBS方案.Wu等[13]提出了抗泄漏CBS,可以防止侧信道攻击.左黎明等[14]也提出了一个短CBS方案. 2022年Khan等[15]将基于证书签名方案应用于工业物联网系统,为其提供安全保障.上述方案都使用双线对,因此计算开销比较大.荣维坚等[16]基于整数分解问题提出了一个可证明安全的基于证书数字签名方案.本文主要目的是基于RSA困难性假设,提出一个新的基于证书签名方案.提高基于证书签名方案的效率,与已有的方案比较表明,所提出的方案在证书生成、签名生成和签名验证、签名长度方面都有明显的优势,可用于对带宽需求较小的系统中.

1 预备知识

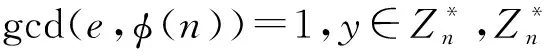
定义2(RSA困难性假设)不存在能以不可忽略的概率解RSA问题的概率多项式算法.

2 基于证书签名

2.1 基于证书签名的定义

基于证书签名方案由下列5个算法组成:

建立算法:该算法通常由权威机构 (certificate authority, CA)进行,用以产生系统主密钥对及公开参数.

用户密钥生成:该算法通常由用户进行,用以产生系统用户的主密钥对.

证书生成:该算法通常由CA进行,用以产生用户签名密钥的组成部分的证书.

签名生成:该算法通常由用户进行,用以产生用户待签名消息的签名.

签名验证:该算法通常由第三方进行,对消息签名对进行验证,判定消息签名对是否有效.

2.2 基于证书签名的安全定义

2.2.1游戏1

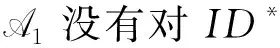
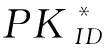
2.2.2游戏2

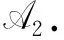
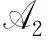
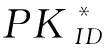
3 本文方案

本文方案的算法组成如下.

建立算法(Setup):输入系统安全参数1k,证书机构选取随机安全大素数{pCA,qCA},然后计算NCA=pCAqCA.选取随机eCA满足gcd(eCAφ(NCA))=1.计算dCA满足eCAdCA=1(modNCA).秘密保存{pCA,qCA,dCA}作为系统主私钥SKCA, 公开{NCA,eCA}作为系统主公钥PKCA.

用户密钥生成(Userkeygen):输入系统安全参数1k,用户ID选取随机安全大素数{pID,qID},然后计算NID=pIDqID.选取随机eID满足gcd(eID,φ(NID))=1,及dID满足eIDdID=1(modNID).设置用户私钥SKID={pID,qID,dID},用户公钥PKID={NID,eID}.

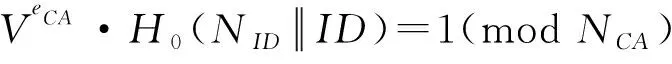
(ⅰ)计算R=reCA(modNCA).

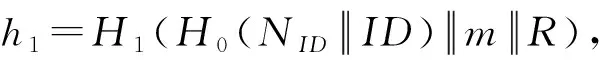
σ2=rVh1(modNCA).

消息m的签名为σ={σ1,σ2}.

签名验证(Verify):当接收者想判定σ={σ1,σ2}是否为消息m在公钥PKCA和PKID下的有效签名时,按下列方式进行签名验证.

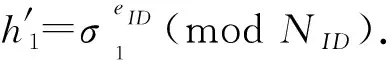
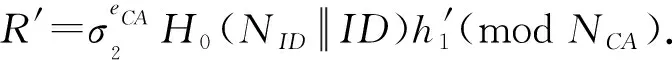
4 安全性证明

4.1 正确性

通过下列简单验算可知方案生成的签名可以通过验证:

reCA(modNCA)=R(modNCA).

4.2 不可伪造性

本文方案的安全性基于RSA困难性假设,即若存在攻击者A可以攻破上述基于证书签名方案,则挑战者C可以解RSA问题.

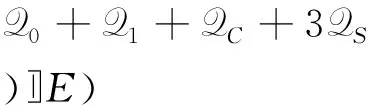
式中E为一次幂指数运算的时间,k为安全参数.

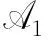
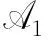
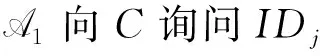
若coin=1,则令

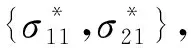
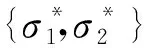
由此可得RSA问题的解

概率分析:根据以上交互模拟可知,当且仅当以下事件都发生时,C可以解RSA问题.

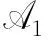
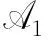
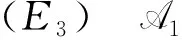
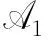
ξ′=Pr[E1∧E2∧E3]=

Pr[E1]·Pr[E2/E1]·Pr[E3/E1∧E2].

若E1发生,则表明在签名询问交互过程中C的应答没有中止,其概率至少为

此外有

式中:E为一次幂指数运算的时间,k为安全参数.

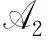
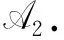
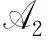
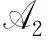
当IDj≠IDt时,令

当IDj=IDt时,C随机选取coin∈{0,1}使得概率Pr(coin=0)=δ.若coin=0,则C令

若coin=1,则C令

无论哪种情形,若H1j=0(modeCA),则重新选择σ,重新计算H1j.

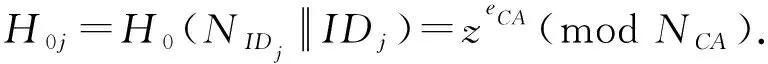
当coin=0时, 签名失败,终止交互.当coin=1时,令

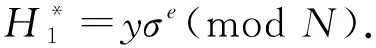
概率分析:根据以上交互模拟可知,当且仅当以下事件都发生时C可以解RSA问题.

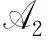
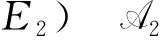
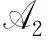
因此C的优势为

ξ′=Pr[E1∧E2∧E3]=

Pr[E1]·Pr[E2/E1]·Pr[E3/E1∧E2].

若E1发生,则表明在私钥询问交互过程中C没有中止.在签名询问交互过程中C的应答没有中止,故

此外

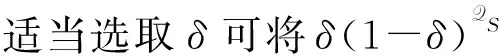
交互模拟所用时间为

由引理1和引理2直接可得下列结论.

定理1在RSA困难性假设和随机预言机模型下,上述方案是能够抵抗敌手适应性存在性不可伪造的.

5 性能分析

5.1 效率比较

双线性对是公认的计算开销比较大的运算,本文方案基于RSA困难问题,不需要双线性对,因此效率较高.表1是本文新方案与近年来提出的已知效率较高方案的比较,其中, P、M、E分别用于标识双线性对运算、标量乘法运算、指数运算.

表1 效率比较

比较结果显示:本文方案在证书生成和签名验证方面是所有方案中最优的.虽然在签名生成方面略差于文献[14]的短签名方案,但通常情况下签名只进行一次,而签名验证可能会由不同人在不同时间进行多次,因此签名验证的效率更有意义.

5.2 实验仿真

我们对本方案进行了实验仿真测试,运行环境如下:操作系统: Windows 10 专业版 64位;主板: 华硕 TUF GAMING B550M-PLUS (WI-FI);处理器: AMD Ryzen 5 3500X 6-Core六核;内存:16 GB(威刚 DDR4 3 200 MHz). 采用Python语言实现本文签名方案.

实验结果见图1.结果表明,本文方案在证书生成、签名生成、签名验证方面非常高效.当选取安全参数1 024位时,对方案进行100次实验测试,证书生成时间平均仅为0.023 s,签名生成时间平均仅为0.051 s,签名验证时间平均仅为0.029 s. 当选取安全参数2 048位时,对方案进行100次测试,方案证书生成时间平均仅为0.163 s,签名生成时间平均仅为0.344 s,签名验证时间平均仅为0.184 s.

图1 不同安全参数方案生成时间

实验结果表明:安全参数1 024位方案是非常高效的,非常适用于带宽较小的设备系统;安全参数2 048位的方案非常适用于对安全要求较高的系统.

6 结语

本文基于RSA困难性假设构造了一种全新的基于证书签名方案,与已有的方案相比,该方案具有明显的效率优势.下一步将研究将本签名方案运用到云计算、物联网、区块链等实际的应用系统中,为数字信息系统提供安全性保障.