折叠交叉立方体的1-好邻诊断度
2023-06-03安婷珠蔡学鹏刘梦瑶杜濛雨
安婷珠, 蔡学鹏, 刘梦瑶, 杜濛雨
(新疆农业大学 数理学院,新疆 乌鲁木齐 830052)
众所周知,互连网络在平行计算及通信系统中发挥着重要作用.一个网络的拓扑结构在数学上通常被抽象地模型化为一个图G=(V(G),E(G)),其中:V(G)是图的顶点集,表示网络处理器的集合;E(G)是图G的边集,表示网络的通信链路集.
本文中术语图与网络可以互换使用且所有的图都认为是无向的、简单的且连通的.
设G=(V,E)是一个图.对于图G的任意非空顶点子集K⊂V(G),以K为顶点集,以两端点均在K中的边的全体为边集所组成的子图称为K在G中的导出子图,记作G[K].对于图G中两个不同的点子集H和K,设HΔK=(H-K)∪(K-H),NH(K)是在H中且与K中的点相邻的点的集合. 特殊地,若K={v},可记作NH(v). 设dG(v)=|NG(v)|是点v在图G中的度. 如果不产生歧义,可省略下标,即记为(d(v),N(v)).δ(G)=min{d(v)|v∈V(G)}表示图G的最小度.对于任意的F⊂V,若v∈V-F且v在G[V-F]中至少有g个邻点,则称F为G的g-好邻故障集.若G-F不连通且G-F的每个连通分支的最小度为g,则称F是G的一个g-好邻割.G的所有g-好邻割中基数最小的g-好邻割的基数称为G的g-好邻连通度,记作k(g)(G).未说明的图论符号和术语可参考文献[1—2].
连通度和诊断度是度量多处理器系统故障诊断能力的重要参数.为了保证计算机系统的可靠性,系统中的故障处理器应该被诊断出来并被非故障处理器替换. Preparata等首次提出了系统级故障诊断模型,称为PMC模型[3],它通过两个相邻的处理器之间相互测试完成系统的诊断. Maeng和Malek 提出了MM*模型[4].在该模型下,一个顶点分别给它相邻的两个顶点发出相同的任务,然后比较它们反馈的结果.传统的诊断度允许点的邻点全为故障点,但是在大型多处理器系统中这种故障出现的概率极小.因此Lai等提出了网络的条件诊断度[5],它限制系统中任意一个处理器至少与一个非故障处理器相邻. 2012年, Peng等通过在系统中限制每个非故障顶点都至少有g个非故障邻点,提出网络(图)的g-好邻诊断度[6]且证明了超立方体在PMC模型下的g-好邻诊断度是2g(n-g)+2g-1(0≤g≤n-3).2016年,Zhang等在文献[7]中通过限制G-F(F⊂V(G))的每个非故障分支中都至少有g+1个顶点,提出了网络(图)g-额外诊断度的概念,并且证明了n-维超立方体Qn在PMC模型下的g-额外诊断度等于n(g+1)-g-0.5g(g-1)(n≥4,0≤g≤n-4).同时,他们还证明了在某些情况下n-维超立方体Qn在MM*模型下的g-额外诊断度等于n(g+1)-g-0.5g(g-1).g-好邻诊断度和g-额外诊断度比传统的诊断度诊断互连网络(图)更为精确.
在平行计算系统中,n-维交叉立方体CQn[8—9]和n-维折叠超立方体FQn[10]是最重要且最流行的两个互连网络.基于交叉立方体和折叠超立方体,文献[11]中提出n-维折叠交叉立方体,记作FCQn.FCQn具有许多重要的特性,如短的直径、短的平均距离和非常低的消息流量密度. 对于FCQn的详细结果可参考文献[11—15].
Adhikari等在文献[15]中证明了FCQn的连通度等于n+1,n≥2.蔡等在文献[14]中确定了k(1)(FCQn)=2n,n≥4, 马等在文献[16]中确定了CQn在PMC模型与MM*下的1-好邻诊断度分别等于2n-1,n≥4和2n-1,n≥5. 本文将证明FCQn在PMC模型与MM*下的1-好邻诊断度分别等于2n+1,n≥5和2n+1,n≥6.
1 预备知识

在MM*模型下,与一个顶点w相邻的两个顶点u,v被分配一个相同的任务,把测试结果反馈给顶点w,再对这两个顶点反馈的结果进行比较.用(u,v)w表示w比较u,v输出的结果,若这两个结果是相同的,则(u,v)w=0;否则,(u,v)w=1.称全部的测试结果为该系统的比较症候,记作σ*.假定3个结点都是非故障的,则测试结果为0; 若w是非故障的,但u,v至少有一个是故障的,则比较结果为1;若w是故障的,则测试结果无论是0或1都是不可靠的.
定义1[17]设G=(V,E)是一个图,对于图G中任意两个不同的g-好邻故障集F1和F2,其中|F1|≤t,|F2|≤t,若F1与F2是可区分的,则G是g-好邻t-可诊断的.
定义2[17]设G=(V,E)是一个图, 使得图G是g-好邻t-可诊断的最大值t称为G的g-好邻诊断度,记作tg(G).
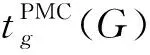
定义3设x=x1x0,y=y1y0是两个二进制字符串,若(x,y)∈{(00,00),(10,10),(01,11),(11,01)},则称x与y是相关的,记作x~y.
n维交叉立方体CQn的顶点集为V(CQn)={bn-1bn-2…b0|bi∈{0,1},0≤i≤n-1},其递归定义如下.
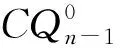
(ⅰ)当n是偶数时,un-2=vn-2;
通过以上定义可得下列推论.
推论1[8]CQn中的两个顶点u=un-1un-2…u0与v=vn-1vn-2…v0是相邻的,当且仅当存在整数l,1≤l≤n,满足下列条件:
(ⅰ)un-1…ul=vn-1…vl;
(ⅱ)ul-1≠vl-1;
(ⅲ)若l是偶数,则ul-2=vl-2;
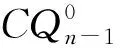

图1是CQ3和FCQ3的图.由定义可知,FCQn是有2n个顶点和(n+1)2n-1条边的(n+1)-正则图.
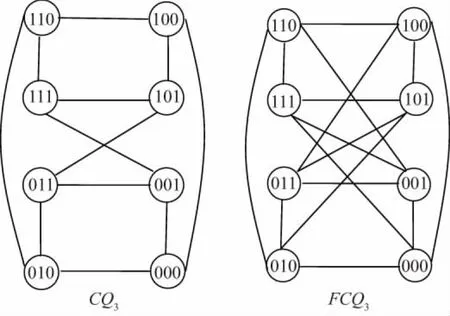
图1 CQ3 和FCQ3

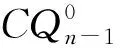
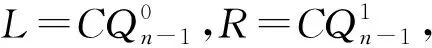
引理1[15]k(FCQn)=n+1,n≥2.
文献[14]中证明了下面的一些结论.
引理2[14]设u和v是CQn中2个不同的顶点,则|NCQn(u)∩NCQn(v)|≤2.
引理3[14]FCQn(n≥4)中不含三长圈.
引理4[14]设u和v是FCQn中两个不同的顶点,则|NFCQn(u)∩NFCQn(v)|≤2.
引理5[14]k(1)(FCQn)=2n,n≥4.
2 主要结论
2.1 折叠交叉立方体网络在PMC模型下的1-好邻诊断度
定理1[3]一个图G=(V,E)在PMC模型下是g-好邻t-可诊断的当且仅当对于V中任意两个不同的顶点数至多为t的g-好邻故障集F1和F2,存在u∈V-(F1∪F2)和v∈F1ΔF2,使得(u,v)∈E(G)(图2).
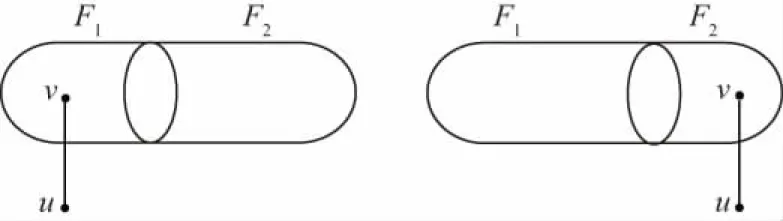
图2 PMC模型下的可区分对(F1,F2)
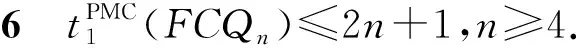



采用反证法证明. 假设存在两个不同的1-好邻故障集F1和F2,其中|Fi|≤2n+1,i=1,2,对任意的u∈V(FCQn-(F1∪F2))和v∈F1ΔF2使得(u,v)∉E(FCQn).不失一般性,假设F2-F1≠∅. 考虑下面两种情形:
情形1V(FCQn)=F1∪F2.
2n=|V(FCQn)|=|F1|+|F2|-
|F1∩F2|≤|F1|+|F2|≤
2n+1+2n+1=4n+2
当n≥5时, 上述不等式矛盾.
情形2V(FCQn)≠F1∪F2.
根据假设V(FCQn-(F1∪F2))与F1ΔF2之间没有边且F1是1-好邻故障集,可得δ(FCQn-(F1∩F2))≥1和δ(FCQn[F1-F2])≥1.
同理,若F1-F2≠∅,则δ(FCQn[F2-F1])≥1,因此,F1∩F2也是1-好邻故障集且|F1∩F2|≥2. 又因V(FCQn-(F1∪F2))与F1ΔF2之间没有边,所以FCQn-F1-F2不连通. 故F1∩F2是FCQn的1-好邻割.根据引理5可得|F1∩F2|≥2n. 因此,|F2|=|F2-F1|+|F1∩F2|≥2+2n=2n+2,这与|F2|≤2n+1相矛盾.
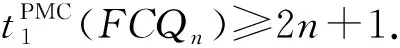
结合引理6和引理7可得下列定理:
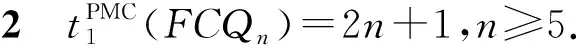
2.2 折叠交叉立方体网络在MM*模型下的1-好邻诊断度
定理3[4]一个系统G=(V,E)在MM*模型下是g-好邻t-可诊断的当且仅当对V中任意两个不同的顶点数至多为t的g-好邻故障集F1和F2,满足下列条件之一(图3):
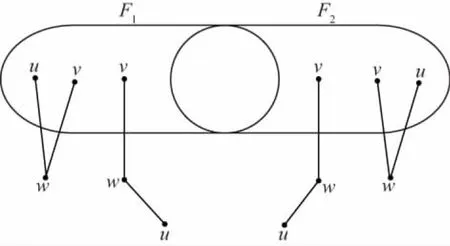
图3 在MM*模型下可区分对(F1,F2)
(ⅰ)存在u,w∈V(G-(F1∪F2))和v∈F1ΔF2满足(u,w),(v,w)∈E(G);
(ⅱ)存在u,v∈F1-F2和w∈V(G-(F1∪F2))满足(u,w),(u,v)∈V(G-(F1∪F2));
(ⅲ)存在u,v∈F2-F1和w∈V(G-(F1∪F2))满足(u,w),(v,w)∈E(G).
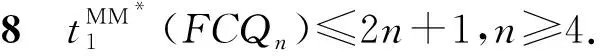
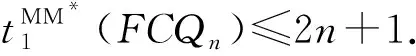
引理9设F1和F2是FCQn(n≥6)中两个不同的1-好邻故障集,其中|Fi|≤2n+1,i=1,2,并且F1、F2不满足定理3中(ⅰ)~(ⅲ), 则FCQn-F1-F2中没有孤立顶点.
证明不失一般性假设F1-F2≠∅.
反证法.假设FCQn-F1-F2中至少存在一个孤立顶点w. 由于F1是一个1-好邻故障集,所以至少存在一点u∈F2-F1使得(u,w)∈E(FCQn). 因为F1、F2不满足定理3中(ⅲ),所以至多存在一点u∈F2-F1使得(u,w)∈E(FCQn). 因此在F2-F1中存在唯一一点u使得(u,w)∈E(FCQn). 同理,当F1-F2≠∅时,存在唯一一点v∈F1-F2使得(w,v)∈E(FCQn).设X是FCQn[V(FCQn-(F1∪F2))]中的孤立点集,则Y=FCQn[V((FCQn)-(F1∪F2)∪X)].因此,当F1-F2≠∅时,对任意的w∈X, 有|NF1∩F2(w)|=n-1.由|F2|≤2n+1可知
|X|(n-1)≤
(|F2|-1)(n+1)≤2n(n+1)=2n2+2n.
由于n≥6,所以|X|<2n+6,若V(Y)=∅,则有
2n=|V(FCQn)|=|F1∪F2|+|X|=
|F1|+|F2|-|F1∩F2|+|X|<
2(2n+1)-(n-1)+2n+6=5n+9.
当n≥6时, 上式矛盾. 所以,V(Y)≠∅. 因为F1,F2不满足定理3中(ⅰ)且δ(Y)≥1,所以V(Y)与F1ΔF2之间没有边相连.因此,F1∩F2是FCQn的点割且δ(FCQn-(F1∩F2))≥1,即F1∩F2是FCQn的一个1-好邻割.根据引理5知|F1∩F2|≥2n.因为|F1|≤2n+1,|F2|≤2n+1且F1-F2和F2-F1都非空,所以|F1-F2|=|F2-F1|=1.于是,设F1-F2={v1}和F2-F1={v2},从而对于任意的w∈X有(w,v1),(w,v2)∈E(FCQn),由引理3可知v1与v2至多有两个公共邻点.因此FCQn-F1-F2至多有两个孤立点.下面考虑两种情形:
情形1FCQn-F1-F2中恰有一个孤立点v,则(v,v1),(v,v2)∈E(FCQn)且(NFCQn(v)-{v1,v2})⊆F1∩F2.因为FCQn不包含三长圈,所以
(NFCQn(v1)-{v})⊆F1∩F2,
(NFCQn(v2)-{v})⊆F1∩F2,
(NFCQn(v)-{v1,v2})∩(NFCQn(v1)-{v})=∅,
(NFCQn(v)-{v1,v2})∩(NFCQn(v2)-{v})=∅.
根据引理3知v1与v2至多有两个公共邻点,所以|(NFCQn(v1)-{v})∩(NFCQn(v2)-{v})|≤1.因此,
|F1∩F2|≥|NFCQn(v)-{v1,v2}|+
|NFCQn(v1)-{v}|+
|NFCQn(v2)-{v}|-1=
(n-1)+n+n-1=3n-2.
于是
|F2|=|F2-F1|+|F1∩F2|≥
1+3n-2=3n-1>2n-1,n≥6.
这与|F2|≤2n+1矛盾.
情形2FCQn-F1-F2中恰有两个孤立点v和v′,则
{(v,v1),(v,v2),(v′,v1),(v′,v2)}⊆E(FCQn),
(NFCQn(v)-{v1,v2})⊆F1∩F2,
(NFCQn(v′)-{v1,v2})⊆F1∩F2.
因为FCQn不包含三长圈,所以
(NFCQn(v1)-{v,v′})⊆F1∩F2,
(NFCQn(v2)-{v,v′})⊆F1∩F2.
又因任意两点至多有两个公共邻点,所以(NFCQn(v)-{v1,v2}),(NFCQn(v′)-{v1,v2}),(NFCQn(v1)-{v,v′})和(NFCQn(v2)-{v,v′})中任意两个集合在F1∩F2中都没有公共点.因此
|F1∩F2|≥|NFCQn(v)-{v1,v2}|+
|NFCQn(v′)-{v1,v2}|+
|NFCQn(v1)-{v1,v2}|+
|NFCQn(v2)-{v,v′}|=
4(n-1)=4n-4.
于是,
|F2|=|F1-F2|+|F1∩F2|≥
1+4n-4=4n-3>2n+1(n≥6).
这与|F2|≤2n+1矛盾.
综上所述,FCQn-F1-F2中没有孤立点.


反证法. 假设存在两个不同的1-好邻故障集F1和F2,其中|Fi|≤2n+1,i=1,2,不满足定理3中(ⅰ)~(ⅲ).不失一般性, 假设F2-F1≠∅.考虑下面两种情形:
情形1V(FCQn)=F1∪F2.
2n=|V(FCQn)|=|F1|+|F2|-|F1∩F2|≤
|F1|+|F2|≤2n+1+2n+1=4n+2.
当n≥6时,上述不等式矛盾.
情形2V(FCQn)≠F1∪F2.

根据引理8和引理10可得下列结论:
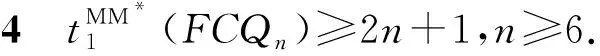
3 结语
本文以n-维折叠交叉立方体网络FCQn为研究对象,在FCQn的拓扑性质和k(1)(FCQn)=2n,n≥4的基础上,进一步证明了在PMC模型与MM*模型下FCQn的1-好邻诊断度分别为2n+1,n≥5和2n+1,n≥6.
