含有间隙的Wiener系统的非光滑卡尔曼滤波的状态估计
2023-06-02李海芬谢迎新张明月
李海芬,黎 冠,谢迎新,张明月
(华北科技学院 电子信息工程学院,北京 东燕郊 065201)
0 引言
间隙广泛存在于机械传动系统、液压系统[1,2]中。以伺服液压传动装置为例,设伺服电机的输入电压信号u(k)和位移输出x(k),这时伺服电机可以看成是一个2阶动态线性子系统。由于液压控制阀不可避免地存在油隙(油隙是由摩擦力和机械固定部分的间隙造成),随着机械设备的不停运转,这种特征会越来越明显,这种油隙可以认为是间隙环节,此时的液压传动系统可以看成是一个带间隙的Wiener系统。
存在于系统中的间隙特性具有非光滑的非线性特性,不仅会影响整个系统的控制精度和灵敏度,使得误差变大,性能降低[3],甚至引发不期望的震荡和控制系统的不稳定,进而导致系统的发散[4]。间隙本身除了非光滑这一特性,还具有局部记忆和多值映射等复杂特性,这使得对这类复杂系统进行状态估计更有挑战性。Bai[5]研究了对含有间隙的 Hammerstein系统的进行辨识。Giri[6]研究了一个Wiener Hammerstein模型的激励识别方法。Cerone和Regruto[7]研究对带有间隙输入系统的参数进行辨识。由于间隙特性不是单独存在的,在系统的工作过程中,不可避免的会受到外界信号的干扰,使得所得到的数据会含有一些噪声,对这类系统进行控制之前,必须要得到系统的准确模型。
本文主要提出一种带有切换函数的非光滑卡尔曼滤波器来抑制系统中的噪声,为了说明所提出的非光滑卡尔曼滤波器的有效性,文中在所有参数都相同的条件下,还用传统的卡尔曼滤波器对含有噪声的数据进行处理,结果表明传统的卡尔曼滤波器在设计时没有考虑间隙环节的影响,使得状态估计不能很好的跟踪实际值,而文中提出新的滤波方法能快速准确的跟踪系统的状态,误差也小很多,并能快速收敛到零。因此,从误差的结果来看,带有切换函数的非光滑卡尔曼滤波比传统的卡尔曼滤波的效果要好很多,这也体现了针对这类复杂的系统构建带有切换的函数的卡尔曼滤波器的意义所在。
1 含有间隙的Wiener系统的模型
所谓迟滞Wiener系统就是由一个动态线性环节和一个非线性环节组成的,该系统有如图1所示的结构。u(k)是整个Wiener系统的输入信号,L1(·)表示动态线性环节,y1(k)是动态线性环节的输出,y1(k)和y(k)间为间隙环节,y(k)是表示整个Wiener系统的输出信号。在这个系统中,只有u(k)和y(k)可以直接测量,中间变量y1(k)不能直接测量。
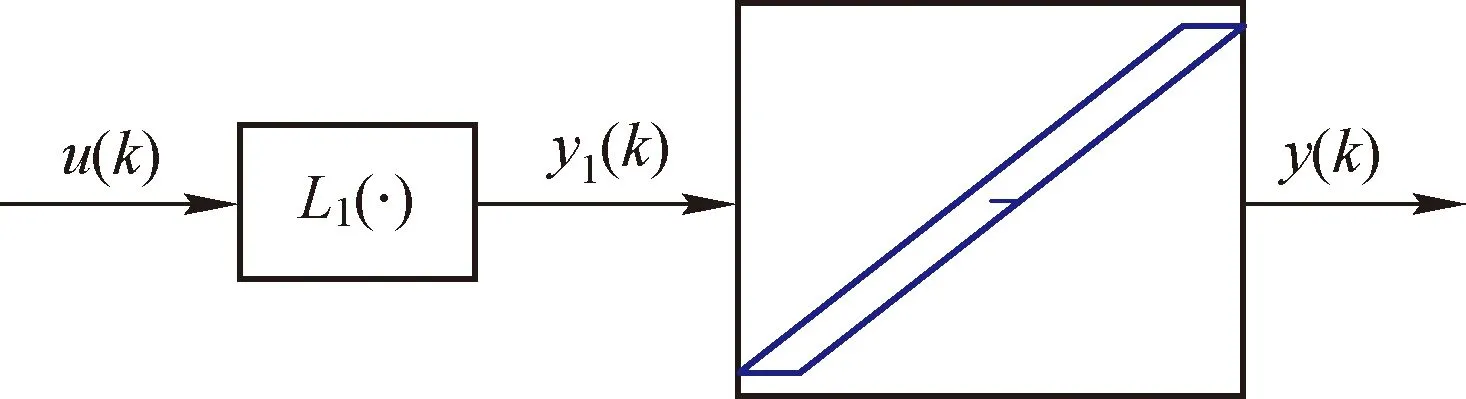
图1 含有间隙的Wiener系统的结构图
1.1 Wiener系统线性部分的模型
设线性子系统的状态空间方程为
(1)
其中,x1∈Rn1×1,A1∈Rn1×n1,B1∈Rn1×1,y1∈R1×1和C1∈R1×n1。式中,x1i表示L1环节的第i个状态变量;A1表示转移矩阵;B1是输入矩阵;y1是动态线性环节的输出;n1表示线性环节的状态变量的维数;u(k)是系统的输入信号。
1.2 Wiener系统间隙部分的模型
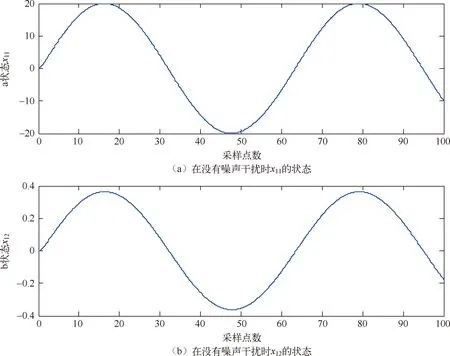
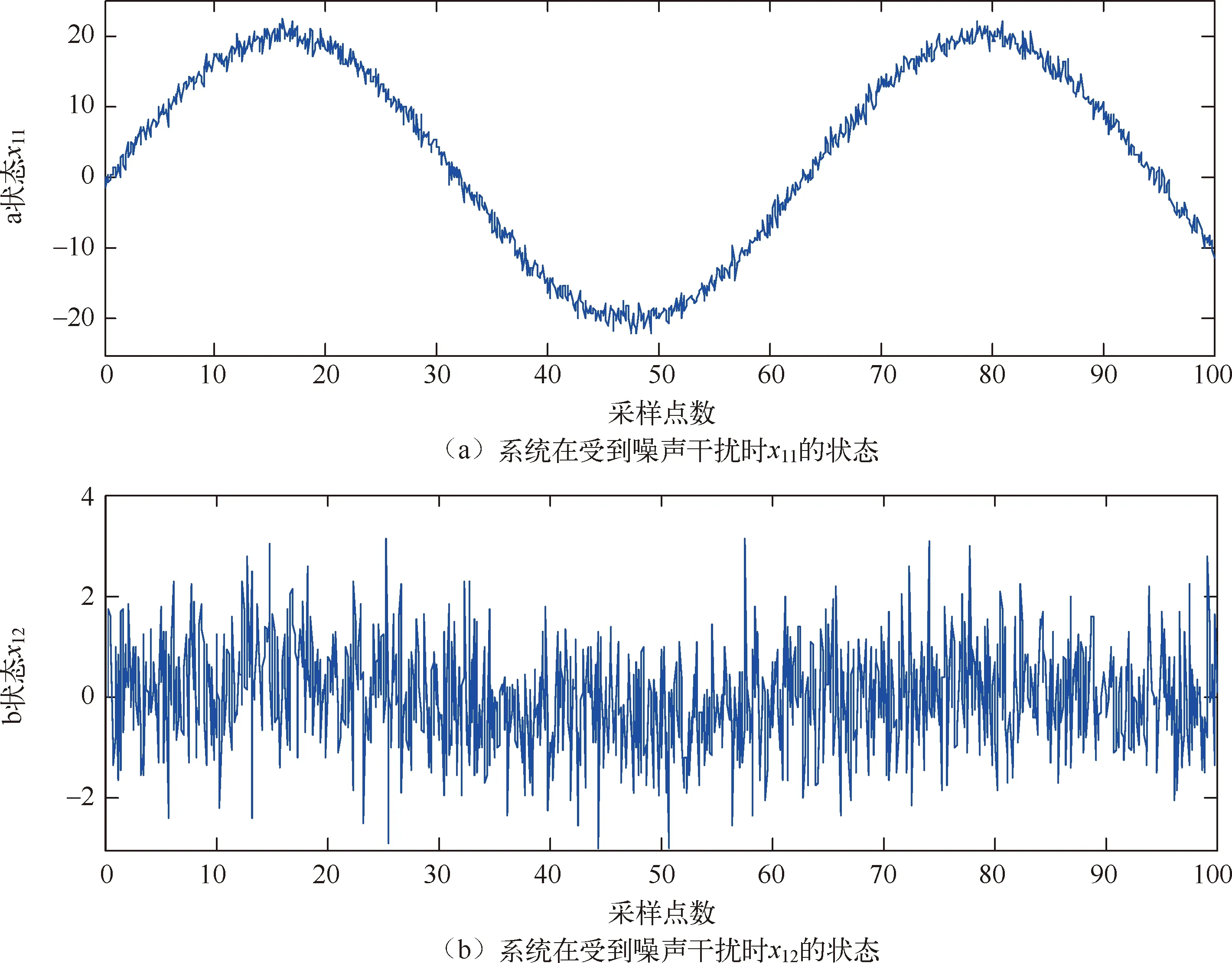
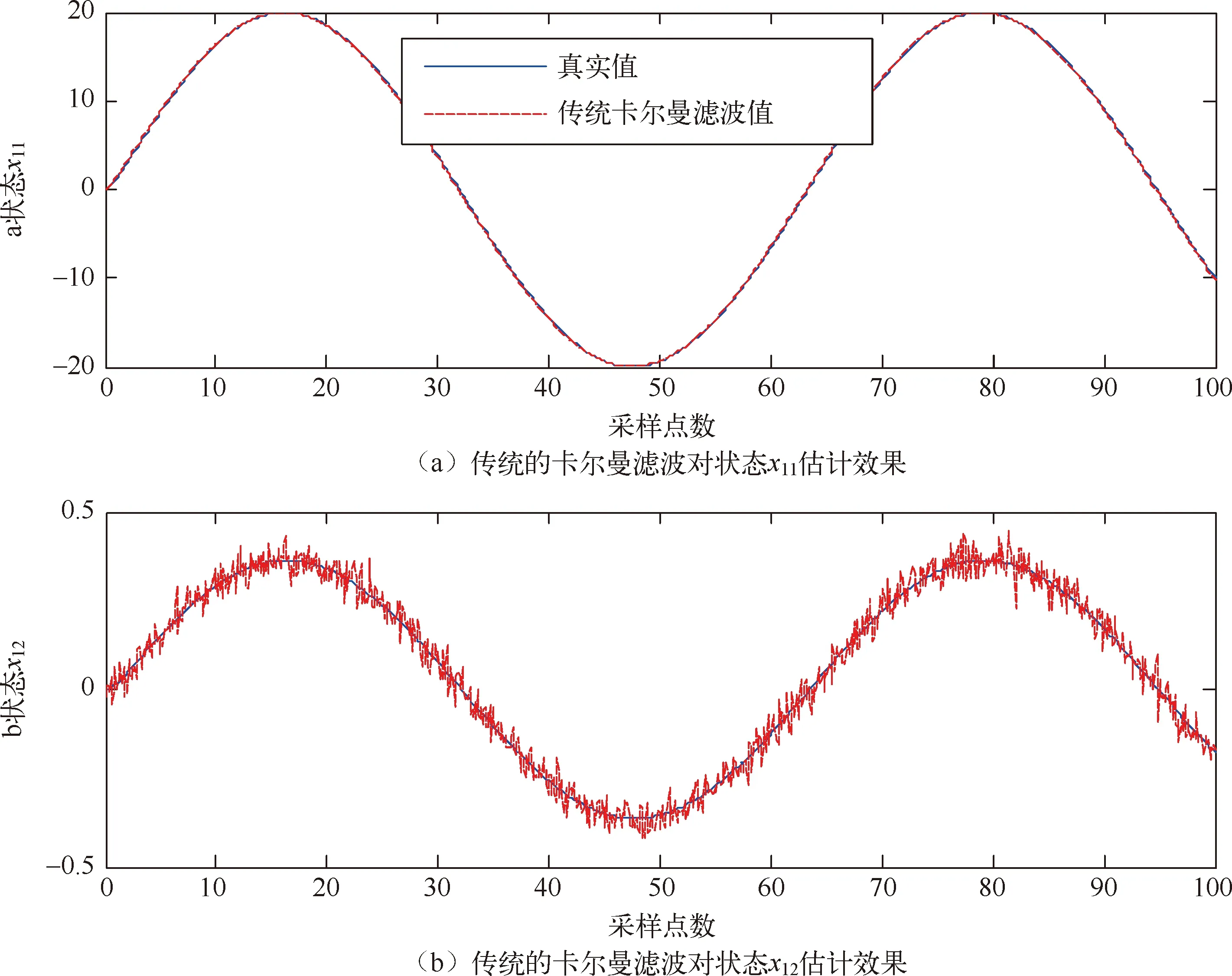
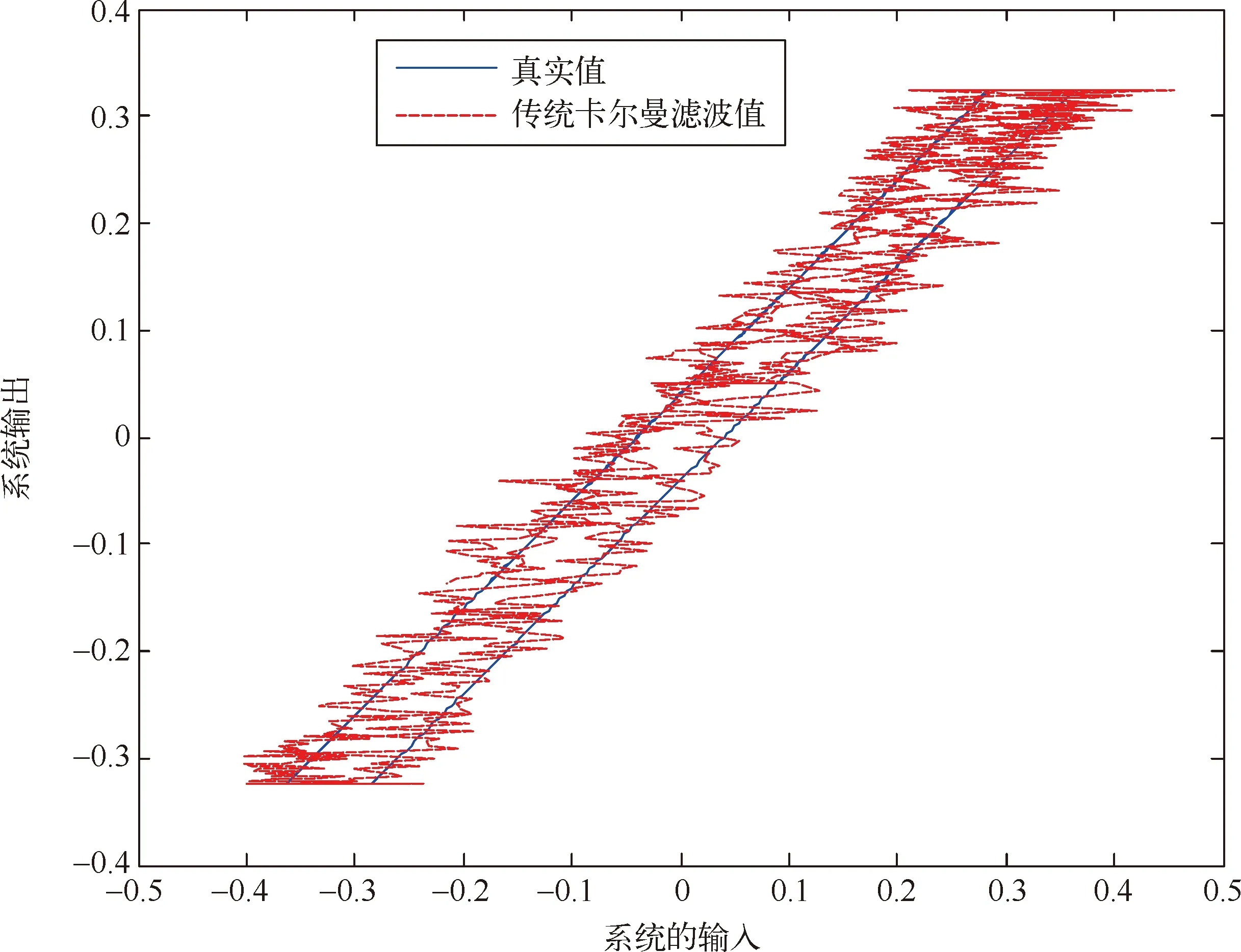
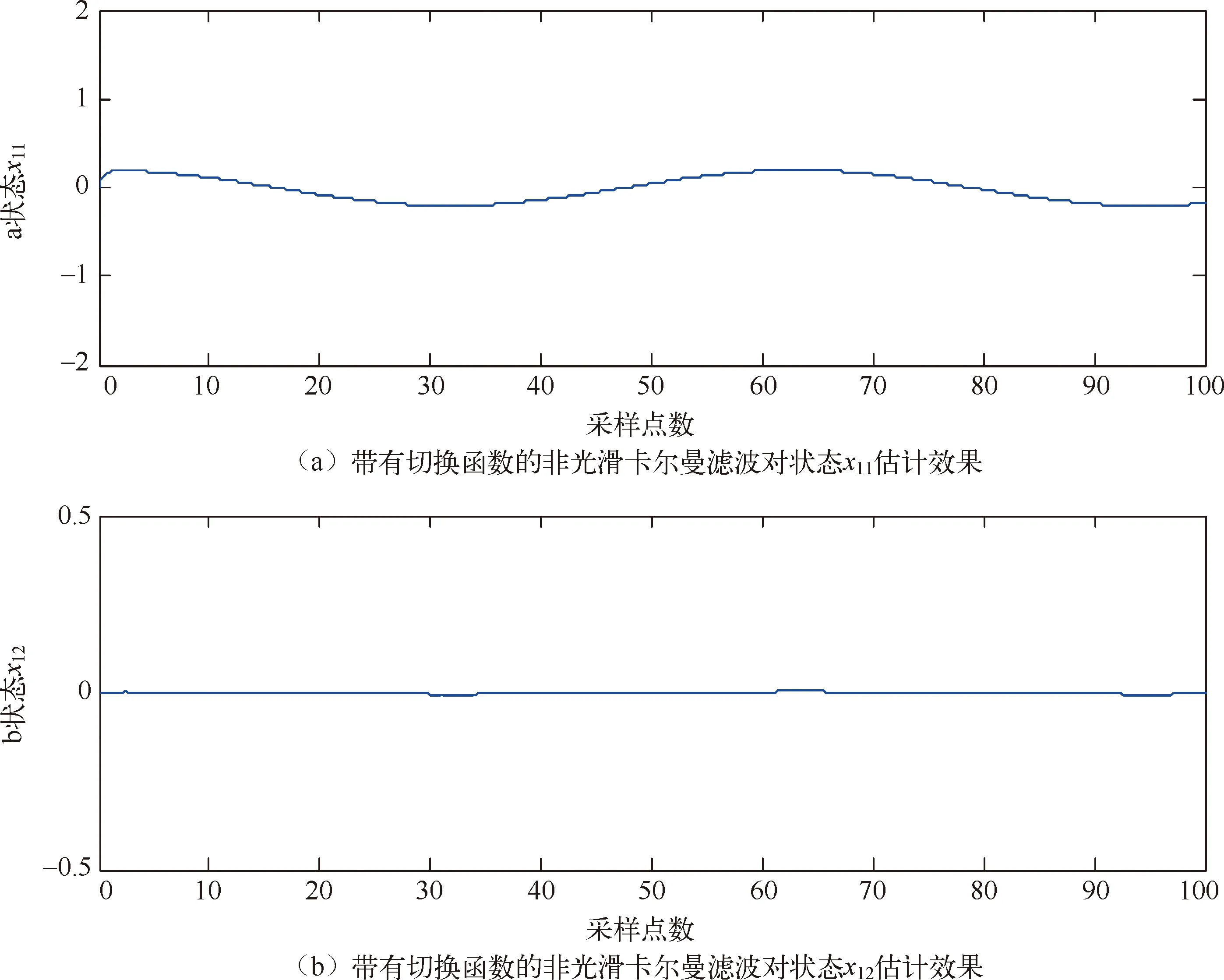
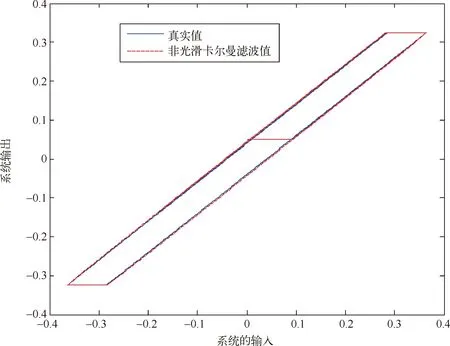
图2中m′1和m′2表示线性区的斜率(0 图2 间隙环节结构图 间隙环节的输出。根据文献[8-10],间隙可以用以下的模型来表示: m(k)=m1+(m2-m1)h(k) (2) z1(k)=m(k)(x(k)-D1h1(k)+D2h2(k)) (3) z(k)=(1-h3(k))z1(k)+h3(k)z(k-1) (4) 其中,h3(k)是切换函数,负责间隙的记忆区和线性区的切换 (5) 从式(5)可看出,当h3(k)=1时,系统工作在记忆区,z(k)=z(k-1);当h3(k)=0,系统工作在线性区,z(k)=z1(k)。将式(3)代入式(4),可以得到 (6) 常用的滤波算法有KF(卡尔曼滤波)、EKF(扩展的卡尔曼滤波)、UKF(无迹卡尔曼滤波)等。卡尔曼滤波算法在光滑线性随机系统的状态估计问题中起了很重要的作用,如导航制导、工业控制、目标跟踪、通信与信号过程和金融[11,12]。EKF[13,14]主要针对非线性系统进行状态估计。UKF和EKF相比,UKF不用对系统进行线性化处理,因此UKF对非线性系统的状态估计的准确性要高。但是以上提到的滤波算法只能适用于光滑的非线性系统,而带有间隙的Wiener系统属于非光滑的非线性系统,这里提出带有切换函数的非光滑卡尔曼滤波器来处理这类复杂的系统在随机噪声下的状态估计问题。考虑如下含有高斯白噪声的间隙Wiener系统: (7) 其中,r(k)和d(k)分别为过程噪声和观测噪声,其均值都为零,协方差矩阵为Q(k)和R(k)的不相关白噪声序列,即 带有切换函数的非光滑卡尔曼滤波公式如下所示: (8) (9) (10) P(k+1)=P(k+1/k)-Φ(k+1)K(k+1)CP(k+1/k) (11) P(k+1/k)=A(k)P(k)AT(k)+Q(k) (12) 设带有间隙的Wiener系统可表示为如下形式: ① 假设第一个线性系统L1为: (13) ② 间隙环节: (14) 图3 在没有噪声干扰时的状态 图4 系统在受到噪声干扰时的状态 图5 传统的卡尔曼滤波估计效果 图6 传统卡尔曼滤波估计误差 图7 传统卡尔曼滤波估计系统的输入输出 在输入条件以及所有参数取值都相同的条件下,用带有切换函数非光滑的卡尔曼滤波器对含有间隙的Wiener系统的状态模型进行滤波。图8是用带有切换函数的非光滑卡尔曼滤波器对含有噪声的系统进行状态估计图。图中实线(蓝色)是系统的真实值,虚线(红色)是带有切换函数的非光滑卡尔曼滤波值。图8(a)是状态x11的滤波结果图。图(b)是状态x12的滤波结果图。图9是估计的状态误差值,其中子图带有切换函数的卡尔曼滤波器对状态x11的估计误差图。图9(b)是用带有切换函数的卡尔曼滤波器对状态x12的估计误差图。从图9中可以看出,状态x12误差要比用传统卡尔曼滤波器的误差要小,这是由于在状态估计时,考虑间隙环节的影响。图10是用带有切换函数的非光滑卡尔曼滤波器估计的Wiener系统的输入输出图。从图9和图10可以看出,带有切换函数的卡尔曼滤波器能准确快速的跟踪系统的各个状态变量的真实值,在模型的准确性和误差的收敛速度上都要优于传统的卡尔曼滤波器。 图8 带有切换函数的非光滑卡尔曼滤波估计效果 图9 带有切换函数的非光滑卡尔曼滤波估计误差 图10 带有切换函数的非光滑卡尔曼滤波估计系统输入输出 (1) 本文提出一种带有切换函数的非光滑卡尔曼滤波器,对含有噪声的间隙Wiener系统进行状态估计。 (2) 为了说明所提出方法的有效性,本文在输入条件及所有参数值都相同的情况下用传统的卡尔曼滤波器对其进行状态估计。结果表明带有切换函数的非光滑卡尔曼滤波器能准确的估计系统的状态。而传统的卡尔曼滤波器由于没有考虑间隙的记忆性和多值映射性,比系统估计的误差要大一些。 (3) 本文得到带有切换函数的卡尔曼滤波器不论是在估计的精度还是误差的收敛速度都要优于传统的卡尔曼滤波器,这也为下一步研究系统的精确控制奠定了基础。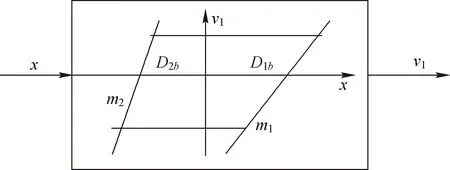
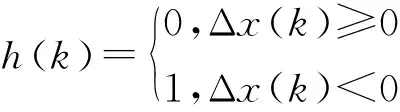

2 带切换函数的非光滑卡尔曼滤波器
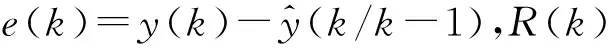
3 仿真结果
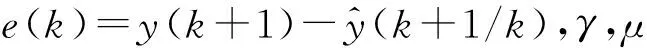
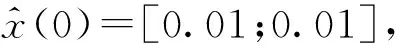


4 结论
