CO2/N2在烟煤无烟煤中的吸附分析
2023-06-02程根银汤晓辰司俊鸿
程根银,汤晓辰,司俊鸿
(华北科技学院,北京 东燕郊 065201)
0 引言
目前,占能源消费的大部分仍是煤炭,因此保证煤炭开采的稳定至关重要。但在煤炭生产过程中经常发生事故,其中矿井火灾是煤矿井下最常发生的事故之一。据统计,近十年因井下煤自燃发生的火灾事故所造成的死亡人数高达166人[1]。矿井火灾发生的原因有很多,但造成火灾的大多数情况是由于采空区内部的破碎煤体发生煤炭自燃[2]。主要原因是煤与氧之间发生化学反应并达到煤的临界温度,最终导致火灾发生。在防治煤炭自燃技术中,向采空区注气技术是目前为止最有效的措施之一,其特点主要是安全,环保。目前,主流的气体是以CO2和N2为主,这些气体在煤分子表面形成屏障,减少煤与氧气碰撞次数,有效防止煤炭自燃。
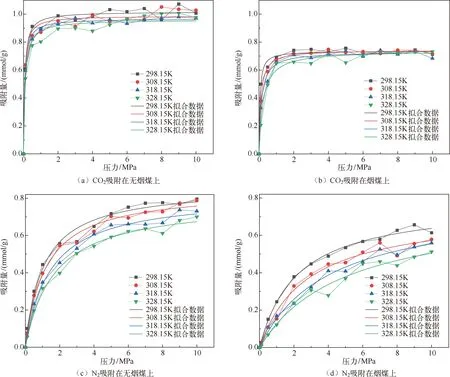
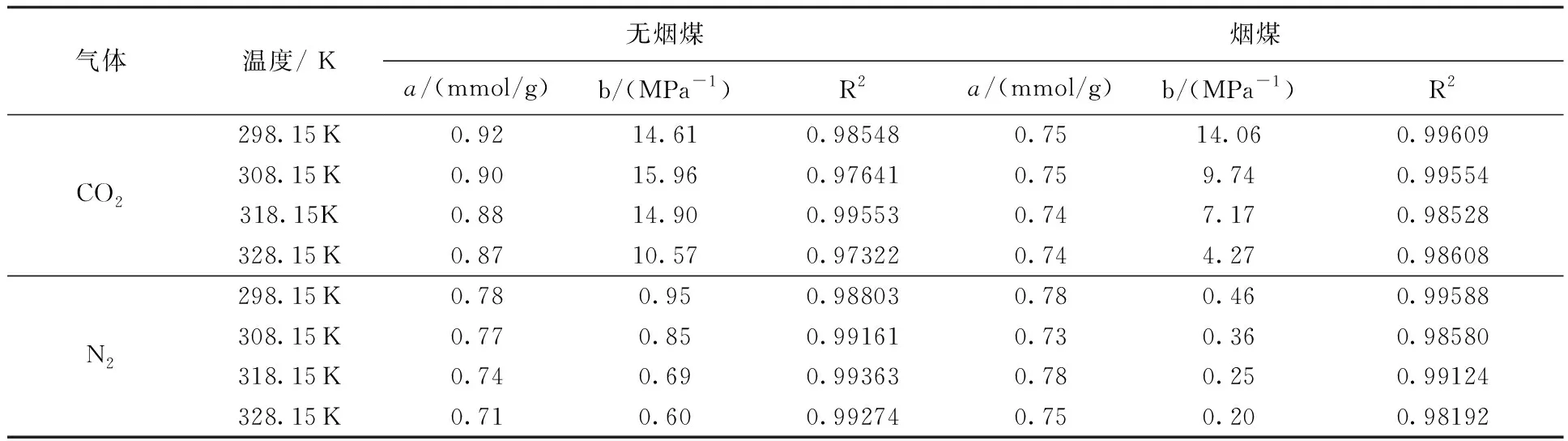
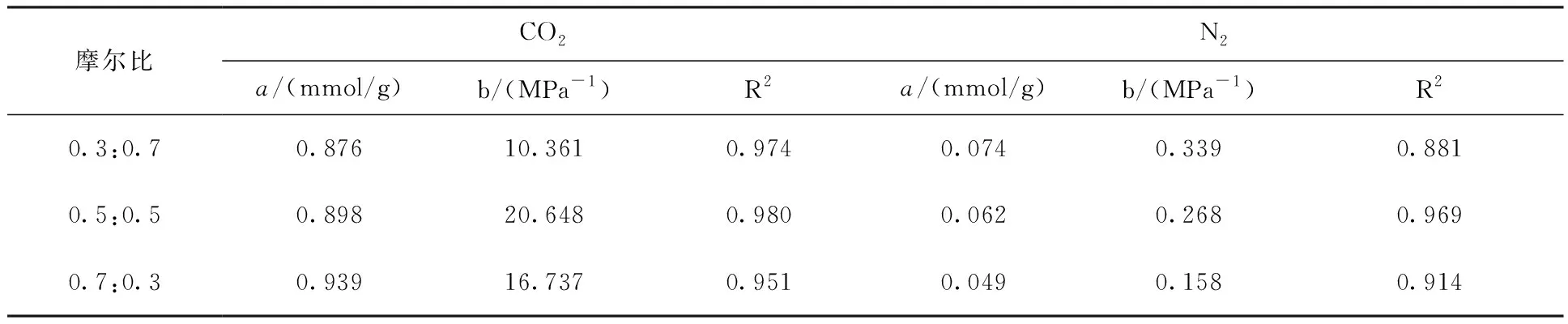
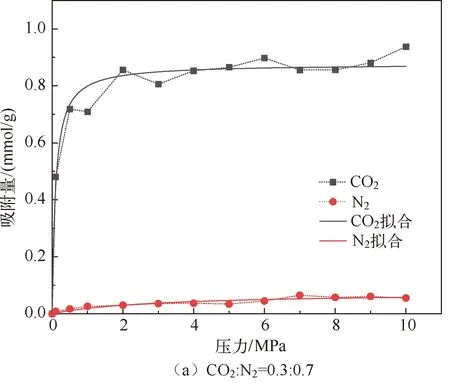
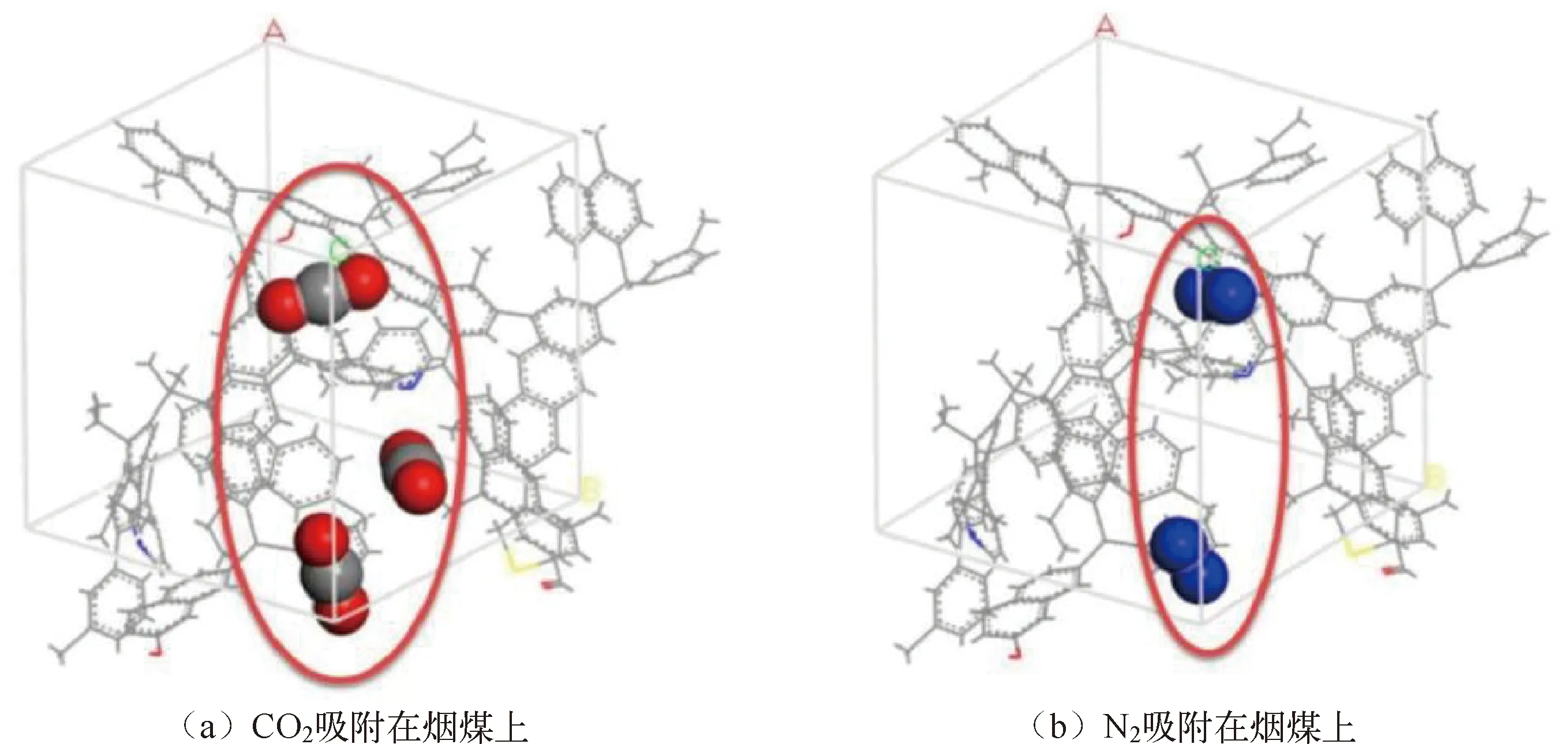
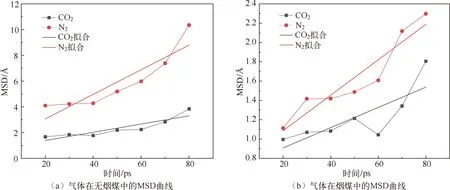
分子模拟对于从微观角度研究煤吸附井下气体有着重要意义,研究者人员首先通过分子模拟研究不同煤分子的结构,孟筠青[3]通过核磁共振等技术结合分子模拟得到真实的煤分子构型并分析煤的孔隙结构;随后,其他学者结合吸附理论研究微观条件下煤对不同气体的吸附特征,刘宇[4]运用分子模拟的方法研究甲烷在煤中吸附行为发现煤中不同基团对甲烷的吸附能力有所不同。鲁金涛等[5]对氧气的吸附进行了模拟研究。结果表明:在氧气的吸附过程中,吸附作用逐渐转为化学吸附,同时静电相互作用增强。另外,还有学者对煤吸附混合气体进行了研究,金智新等[6]模拟了电厂烟注入煤分子的吸附行为。结果表明:气体的竞争吸附能力为 CO2>O2>N2。但对于煤吸附气体的分子模拟研究到目前为止,主要是针对单一煤分子吸附气体分子的行为特征展开的,尤其是对褐煤的研究最多。程敢等[7]主要对褐煤分子中各个含氧官能团对气体的吸附相互作用的研究。结果表明:二氧化碳是气体中吸附能力最强的,氧气则次之,H2O分子由于氢键作用吸附能远大于其他气体。相建华等[8]模拟了不同温压下气体在煤分子的吸附情况。发现单组分情况下,吸附量相对大小为 CH4< CO2 基于以上研究背景,对CO2与N2在无烟煤与烟煤中的吸附特征进行研究。选取烟煤和无烟煤分子模型,通过数值模拟方法运用Materials Studio软件对比CO2和N2在两种煤分子模型中的吸附和扩散行为,为后续研究提供参考。 选取烟煤分子(C201H170N2O3S)[10]和无烟煤分子(C182H112O7)[11]。他们的模型合理,且碳含量相近,因此选择了它们进行模拟。烟煤和无烟煤的基本单元分别如图1所示。 图1 煤分子基本单元 建立煤的分子模型运用到Materials Studio软件中的Amorphous Cell模块,经过优化后的煤分子模型如图2所示。烟煤晶胞大小为a=14.9Å,b=14.9Å,c=14.9Å;无烟煤晶胞大小为a=14.4Å,b=14.4Å,c=14.4Å。采用半径为1.6Å的分子探针分别得到无烟煤分子孔隙的Connolly自由体积大小为269.41Å3,烟煤分子孔隙的Connolly自由体积大小为208.12Å3。 图2 煤分子结构模型 蒙特卡洛模拟的基本思想是将求解的问题转化为随机事件的概率,其本质是利用随机数进行模拟计算。蒙特卡洛模拟理论基础则是一大类计算算法的集合,依靠重复的随机抽样来获得数值结果。吸附模拟采用巨正则系综蒙特卡洛方法计算,在Materials Studio 2019软件中吸附模块的Fixed pressure Task进行。在Fixed pressure Task任务中设置温度298.15K、308.15K、318.15K和328.15 K,压力范围选取 0~10MPa。力场与相互作用等参数设置见表2。蒙特卡洛模拟在Fixed pressure Task模块中进行统计抽样实验计算,在指定的温度和压力下计算出气体的吸附量,将不同温压下的气体吸附量进行拟合得到不同气体的等温吸附曲线。CO2和N2的摩尔质量、临界温度、临界压力和偏心因子等参数见表1[9],压力和逸度的换算由Peng-Robinson公式实现[12,13]。通过Langmuir公式获得了不同温度条件下各组分气体的吸附等温线[14,15]。Langmuir公式为: 表1 CO2与N2的物理性质 表2 吸附模拟相关参数设置 (1) 式中,a是压力趋于无穷大时的极限吸附量,mmol/g;b是吸附常数,MPa-1。 根据模拟结果得出的吸附量N单位为‘average molecules/cell’,通过下述等式将其转换为‘mmol/g’: (2) 式中,N表示吸附量,mmol/g;Nam表示吸附分子个数;Na表示晶胞个数;Ms为单个晶胞的分子量。 多组分气体混合物中两组分之间的竞争程度大小可以用吸附选择性来表示,两种气体的吸附选择性可用下式(3)计算[16]: (3) 式中,xi和xj分别表示吸附相中i和j物质的摩尔分数;yi和yj分别表示自由相中i和j物质的摩尔分数。 吸附位置的定位在吸附模块中的locate进行并在图像上显示。locate中力场参数等设置与Fixed pressure Task中设置相同。 分子动力学模拟是一种通过计算机模拟分子或分子体系的结构和性质的方法。其理论基础依据为牛顿力学,通过模拟分子的运动,求解整个系统的热力学量以及其他宏观性质。采用分子动力学模拟能够计算出分子的均方位移进而从微观层面得到分子间的扩散系数,直观地研究其扩散行为。 首先采用蒙特卡洛方法,在1.0MPa和298.15K时分别让烟煤和无烟煤表面模型中吸附CO2分子和N2分子。分子动力学模拟时间为100ps,采用NVT正则系综。其他设置参数与1.2节相同。 均方位移(MSD)表示分子的平均运动和,MSD可以通过分子动力学模拟得到,其公式如(4)所示[7]: (4) 扩散系数指分子均方位移随时间的变化率[9],可以由式(5)得出: (5) 式中,D为扩散系数;N是粒子数,ri(t)和ri(0)分别是分子i在时间t和0的位矢。 气体逸度系数与压力的关系如图3所示。总体上看,两种气体在恒压、升温条件下,气体逸度系数呈上升趋势。分开来看,可以发现,N2的逸度系数变化小于CO2的逸度系数变化。在0~10MPa压力范围内,N2的逸度系数从0.974上升到1,CO2的逸度系数从0.468上升到1。CO2逸度系数与压力的关系如图3所示。在298.15K,曲线梯度突然变化,原因主要是CO2的临界温度较高,为304.13K,临界压力为7.38MPa。在298.15K,当压力超过6MPa后,CO2由气态转变为液态,逸度系数迅速下降。两种气体的逸度系数受温度和压力的影响顺序为CO2>N2。 图3 不同温度下气体逸度系数与压力之间的关系 2.2.1 一元组分吸附 如图4所示,无论是烟煤还是无烟煤,在相同的压力条件下,随着温度从初始的298.15K升高到328.15K,两种气体的吸附量都有不同程度的减小。此结果与李龙建[17]的结论一致,充分说明温度的升高会抑制气体的吸附,并促进解吸。在吸附过程中,压力从0MPa升高到10MPa,吸附等温线逐渐趋于平坦,说明气体的吸附速率与压力成反比。在烟煤中,压力范围在0~1.5MPa气体吸附速率较快;无烟煤中,压力范围在0~1MPa气体吸附速率较快。 图4 CO2与N2在不同温度下的吸附等温线 在温度分别为298.15K、308.15K、318.15K和328.15K,压力范围为0~10MPa内,比较图4中(a)和(b),可以看出烟煤中CO2的吸附量为0.208~0.752mmol/g,无烟煤中CO2的吸附量为0.538~1.007mmol/g。根据图4中(c)和(d)可以发现,烟煤中N2的吸附量为0.012~0.613mmol/g,无烟煤中N2的吸附量为0.055~0.795mmol/g。由上述数据可知,无论烟煤还是无烟煤中CO2的吸附量总是大于N2的吸附量。根据图4可知,无烟煤中CO2与N2吸附等温线趋于平缓后吸附量分别在0.97~1.07mmol/g和0.70~0.80mmol/g范围内,烟煤中CO2与N2吸附等温线趋于平缓后吸附量在0.73~0.75mmol/g和0.45~0.65mmol/g范围内,说明气体在烟煤中的吸附量大于无烟煤中的吸附量。 烟煤和无烟煤在不同温度下的Langmuir拟合参数见表3。其中,参数a和b来自公式(1),a是压力趋于无穷大时的极限吸附容量,而b是吸附常数,与吸附能量有关。Langmuir拟合R2均大于0.95拟合度较高,说明吸附量数据是合理的。根据表3可知,无烟煤中CO2的a值范围为0.90~2.00mmol/g,N2的a值范围为0.70~0.90mmol/g;烟煤中CO2的a值范围为0.70~0.80mmol/g,N2的a值范围为0.70~0.80mmol/g。比较两种煤的a值发现,无烟煤中CO2的a值在各个温度下都大于烟煤中CO2的a值,表明CO2在无烟煤中气体的极限吸附量较烟煤中的极限吸附量要更大,该结果与图4吸附量结果一致。吸附量的大小顺序为CO2> N2。由于CO2的临界温度大于N2的临界温度,因此CO2相较于N2可以更快地达到极限吸附量。综上所述:在同一种煤中CO2的吸附性能相较于N2更强,并且气体在无烟煤中的吸附性能强于烟煤,侧面说明煤阶越高,气体在煤中的吸附性能更强,这与尉瑞等[18]的结果一致。 表3 气体在煤中不同温度下等温吸附线的Langmuir拟合参数 2.2.2 二元组分吸附 图5展示了在无烟煤中308.15K下CO2/N2不同摩尔比的等温吸附曲线。Langmuir拟合参数见表4。观察不同摩尔比的等温吸附曲线可以发现CO2的吸附量远大于N2,两种气体竞争吸附时CO2的竞争吸附优势更大。这是由于CO2与N2的临界温度相比更大,吸附能力更强。当同时向煤中注入两种气体时,CO2会迅速占据有利吸附点位,导致竞争吸附中N2相较于单组份吸附量大大减小。因此,CO2比N2更能有效抑制煤的自燃。从表3可以看出,随着CO2摩尔比的增加,N2的极限吸附量从0.074mmol/g下降至0.049mmol/g下降了33.7%。CO2的极限吸附量从0.087增加到0.093mmol/g,仅变化了7.1%。仍处于较高水平,CO2与N2相比几乎不受摩尔比的影响。同样的尉瑞等[18]通过实验证明CO2比N2在竞争吸附中有更强的吸附能力。 表4 308.15K下CO2与N2的Langmuir拟合参数 图5 不同比例CO2与N2在308.15K下的等温吸附线 图5 不同比例CO2与N2在308.15K下的等温吸附线(续) CO2和N2在不同温度且摩尔比为1:1时的等温吸附线如图6所示。CO2与N2在两种煤中发生竞争吸附的吸附量都呈现相同的变化趋势。对比308.15K和328.15K两种气体的吸附量都随温度升高而降低。这是由于温度升高,气体分子的热运动和动能增加。气体更有可能克服待解吸的煤基质表面上的分子间作用力,从而减少气体吸附量。在不同温度下,CO2的最大吸附量从0.90mmol/g降至0.85mmol/g;N2的最大吸附量仅从0.046mmol/g下降到0.041mmol/g。可以发现对于温度的变化CO2表现得更为敏感,二元气体吸附时N2受到温度影响比CO2更小,这种规律在烟煤中同样适用。 图6 CO2和N2在不同温度下的等温吸附线 如表5所示,对比两种煤在1.0MPa下总吸附量可以发现,温度从308.15K升高至328.15K,CO2与N2两种气体的在无烟煤中总吸附量从0.826mmol/g下降至0.750mmol/g,在烟煤中总吸附量从0.589mmol/g下降至0.545mmol/g。这主要是由于温度升高导致CO2吸附量变化明显,最终呈现为总吸附量随温度下降。 表5 1.0MPa状态下CO2/N2为1:1时总吸附量与温度的关系 2.2.3 吸附选择性 N2/CO2吸附选择性如图7所示,随着温度从298.15K升高至328.15K,N2/CO2吸附选择性范围从0.0045上升为0.0124。不同摩尔比下的N2/CO2吸附选择性也随温度同样变化,表明在煤中CO2的吸附选择性始终要高于N2,但随着温度升高分子热运动越来越剧烈,分子动能增加,气体分子和吸附剂之间的接触机会也随之增加,使CO2对N2的选择性降低,因此温度升高不利于CO2的竞争吸附。由于CO2对温度更敏感,使SN2/CO2快速增加。随着CO2/N2的摩尔比逐渐升高,在同一温度下N2对CO2的吸附选择性逐渐降低,同时CO2吸附量会随着CO2/N2摩尔比的升高而增大,使得SN2/CO2的值逐渐减小。 图7 0.1MPa下不同比例的N2/CO2选择性随温度的变化 气体在两种煤中单组份吸附的等量吸附热如图8所示。在吸附热大小方面,随着温度从298.15K逐渐升高至328.15K,两种气体并没有发生明显变化。在298.15~328.15K温度范围内,气体吸附热受温度和压力的影响很小。观察图8可以发现,两种气体均为物理吸附。另外,在两种煤中CO2的吸附热始终大于N2的吸附热,说明CO2的吸附能力明显强于N2。并且两种气体吸附于烟煤和无烟煤分子构型的吸附热相差不大,分别维持在36~37kJ/mol 之间与20~23kJ/mol之间。 图8 气体的等量吸附热与温度的关系 表6分别展示了两种气体一元组分和二元组分吸附的等量吸附热数据,可以发现两者吸附热变化不大CO2和N2的吸附热保持稳定。这是因为两种气体在煤中吸附属于物理吸附,竞争吸附不会影响两种气体的吸附热。 表6 吸附热数据 以298.15K和1.0MPa的吸附构型为例,得到了气体分子在烟煤和无烟煤上的吸附位置。通过比较CO2和N2气体分子在烟煤上的吸附位置,可以从图9中发现,CO2和N2都具有相对紧密和集中的吸附位置,主要位于含氧官能团和苯环附近。同样,从图10可以发现,CO2和N2也具有相对紧密的集中吸附位置,位于苯环附近。对比图9和图10发现,无烟煤中吸附的气体分子与烟煤中吸附的气体分子虽然都吸附在苯环附近但吸附的位置不同。出现这种差异的原因是由于无烟煤和烟煤分子中孔隙结构不同造成的。 图9 CO2与N2在无烟煤中的吸附位置 图10 CO2与N2在无烟煤中的吸附位置 图11中(a)和(b)分别为CO2和N2在无烟煤与烟煤中的MSD曲线。其中,根据线性拟合分别得到CO2在无烟煤和烟煤的斜率为0.0319、0.010;N2在无烟煤和烟煤的斜率为0.095、0.0183。将其分别代入到式(5)中,得出CO2在无烟煤和烟煤的扩散系数分别为5.328×10-11m2/s、1.691×10-11m2/s;N2在无烟煤和烟煤的扩散系数分别为1.549×10-10m2/s、3.063×10-11m2/s,即N2在两种煤中的扩散能力大小要强于CO2。原因是CO2相较于N2与煤分子之间有更强的吸附能力阻碍了CO2的扩散。 图11 CO2与N2的MSD曲线图 由上述结果可知,两种气体在无烟煤中的扩散系数都要大于烟煤。这是由于煤中孔隙结构也是影响气体扩散的因素之一,所建立的无烟煤分子模型孔径相比烟煤分子模型要大。因此,会呈现出气体的扩散系数在无烟煤中大于烟煤这种现象。 (1) 在煤分子中,CO2的吸附量大于N2。气体的吸附量与压力成正比,而气体的吸附速率与压力成反比。气体在无烟煤中更容易达到极限吸附量。在同一种煤中,达到吸附极限量由易到难的顺序为CO2>N2。在烟煤与无烟煤分子中,气体扩散能力的大小顺序为 N2>CO2,证明CO2有更强的吸附能力。 (2) CO2和N2在烟煤和无烟煤分子结构模型中具有相似且集中的吸附位置,两种气体都更容易吸附在含氧官能团和苯环附近。CO2和N2的吸附热分别维持在36~37kJ/mol 和20~23kJ/mol范围内,均属于物理吸附,且吸附热对于温度和压强并不敏感。 (3) 在气体吸附过程中CO2相比N2对于温度变化反应更为敏感,因此在温度较高的采空区采用交替注气的方式能够更加有效地防治采空区煤炭自燃。先注入N2,利用N2密度小扩散能力强和较高比热容的特点,稀释采空区氧气浓度并降低温度;再注入CO2,达到阻止煤炭自燃的最佳效果。1 计算方法
1.1 煤模型的选取与构建
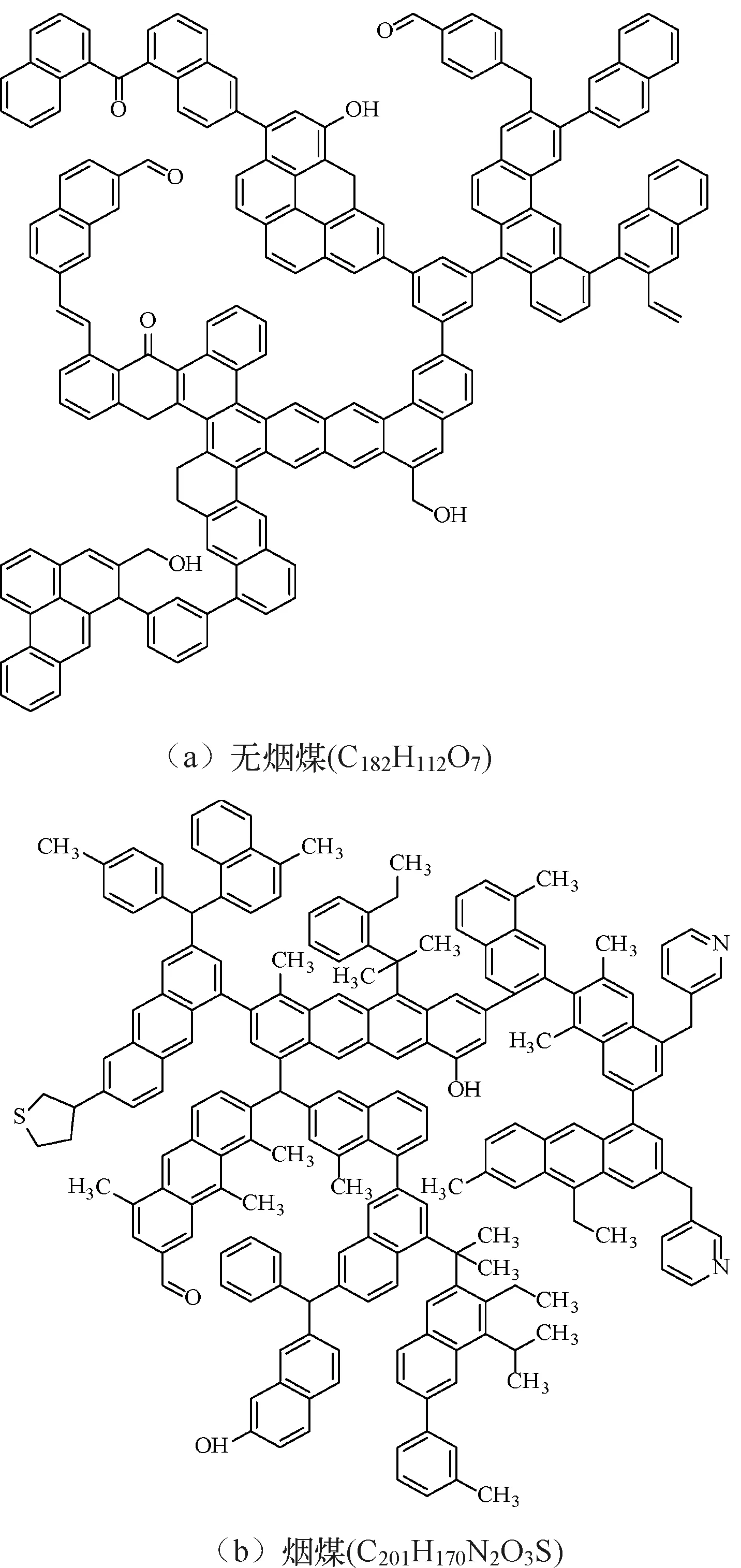
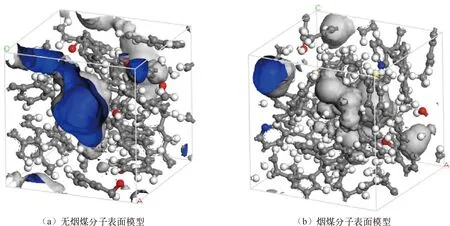
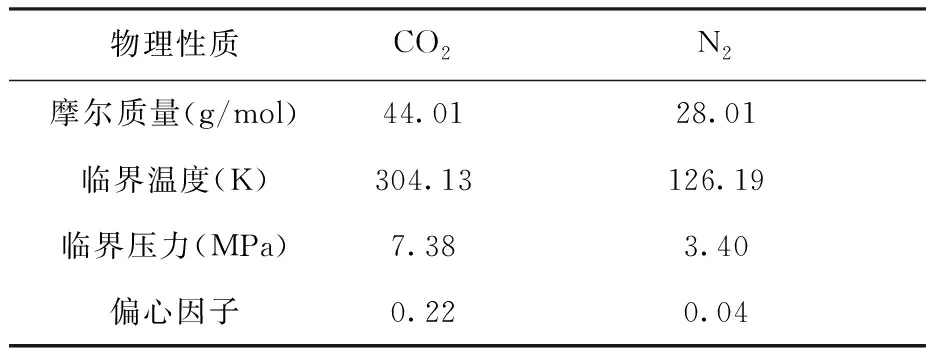
1.2 蒙特卡洛模拟

1.3 分子动力学模拟
2 结果与讨论
2.1 压力与逸度的关系
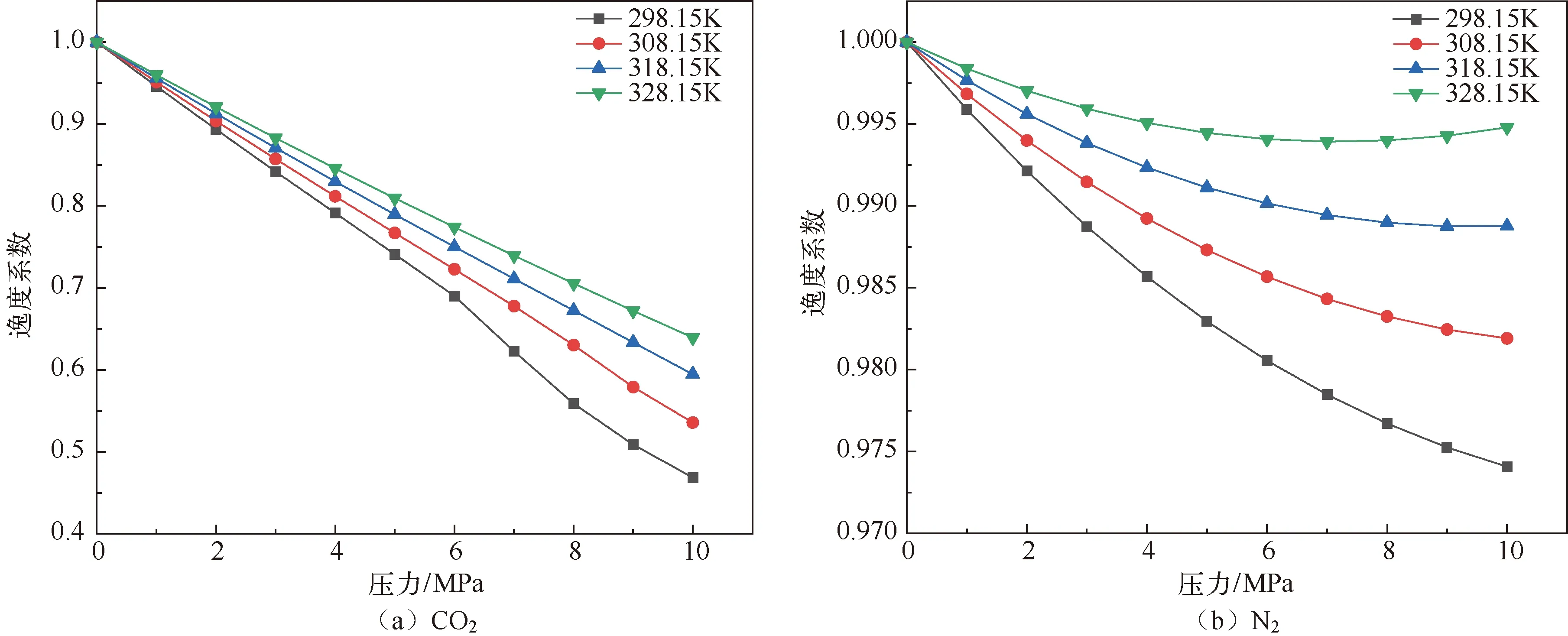
2.2 吸附量与吸附选择性
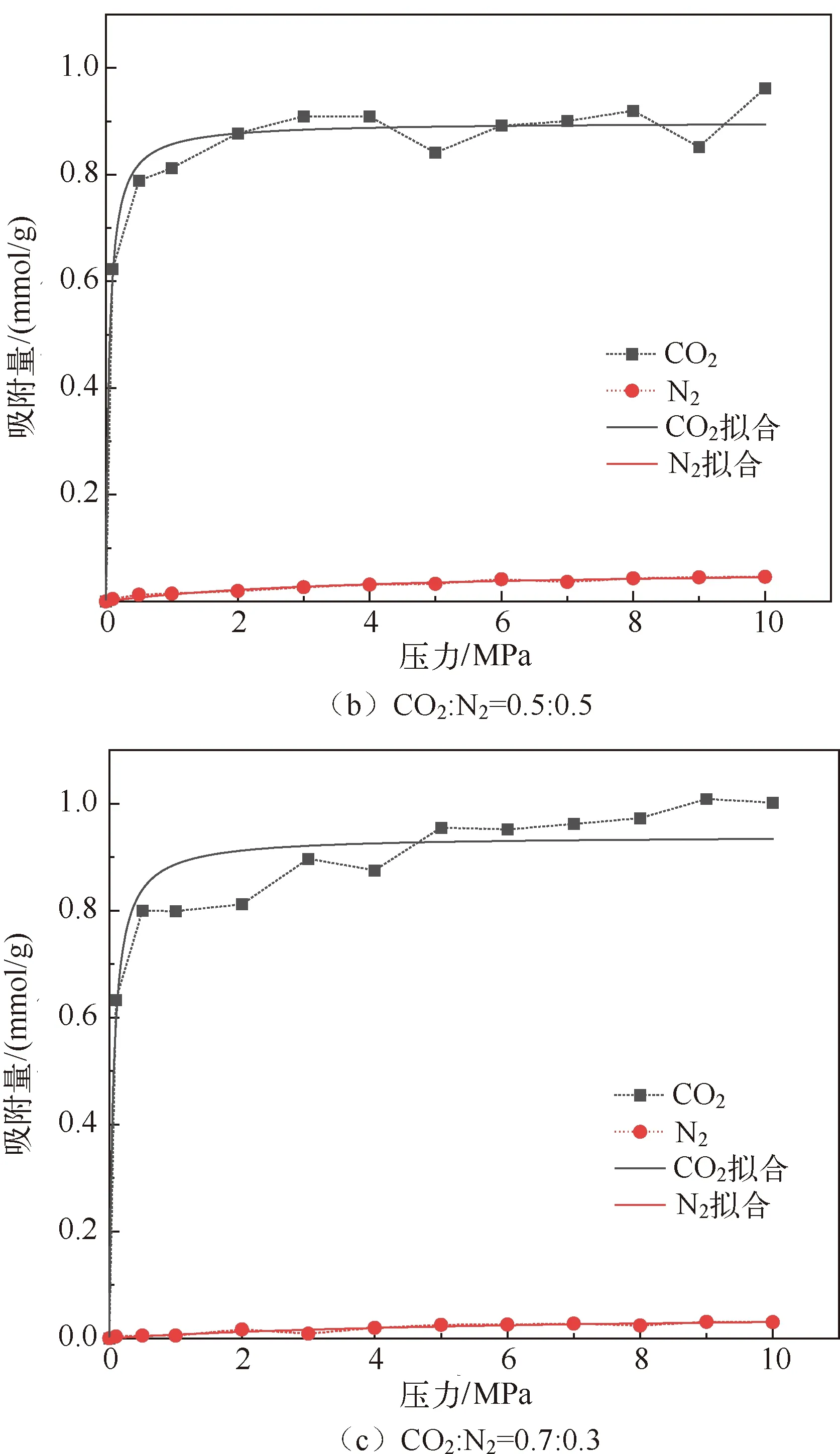

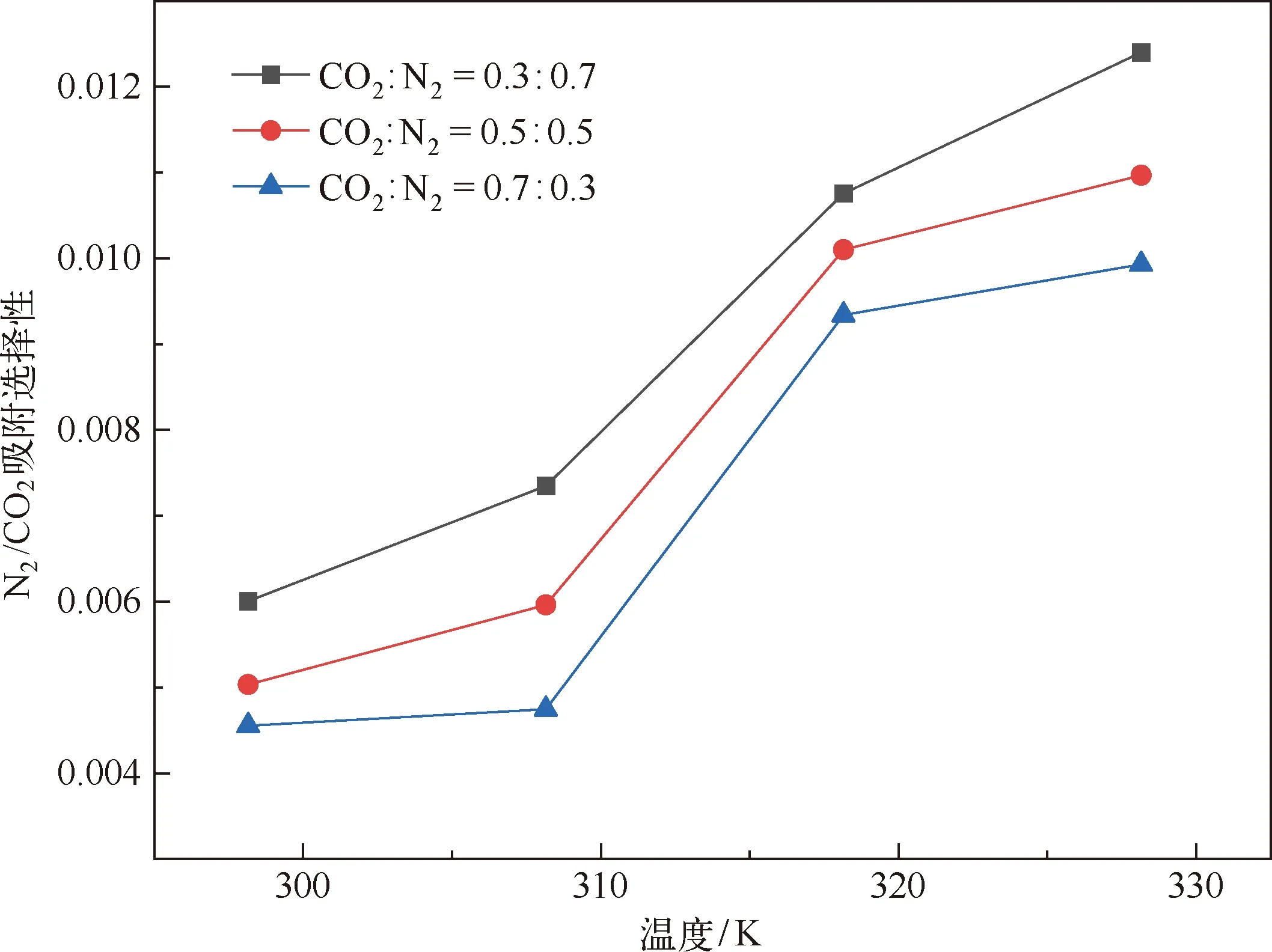
2.3 等量吸附热
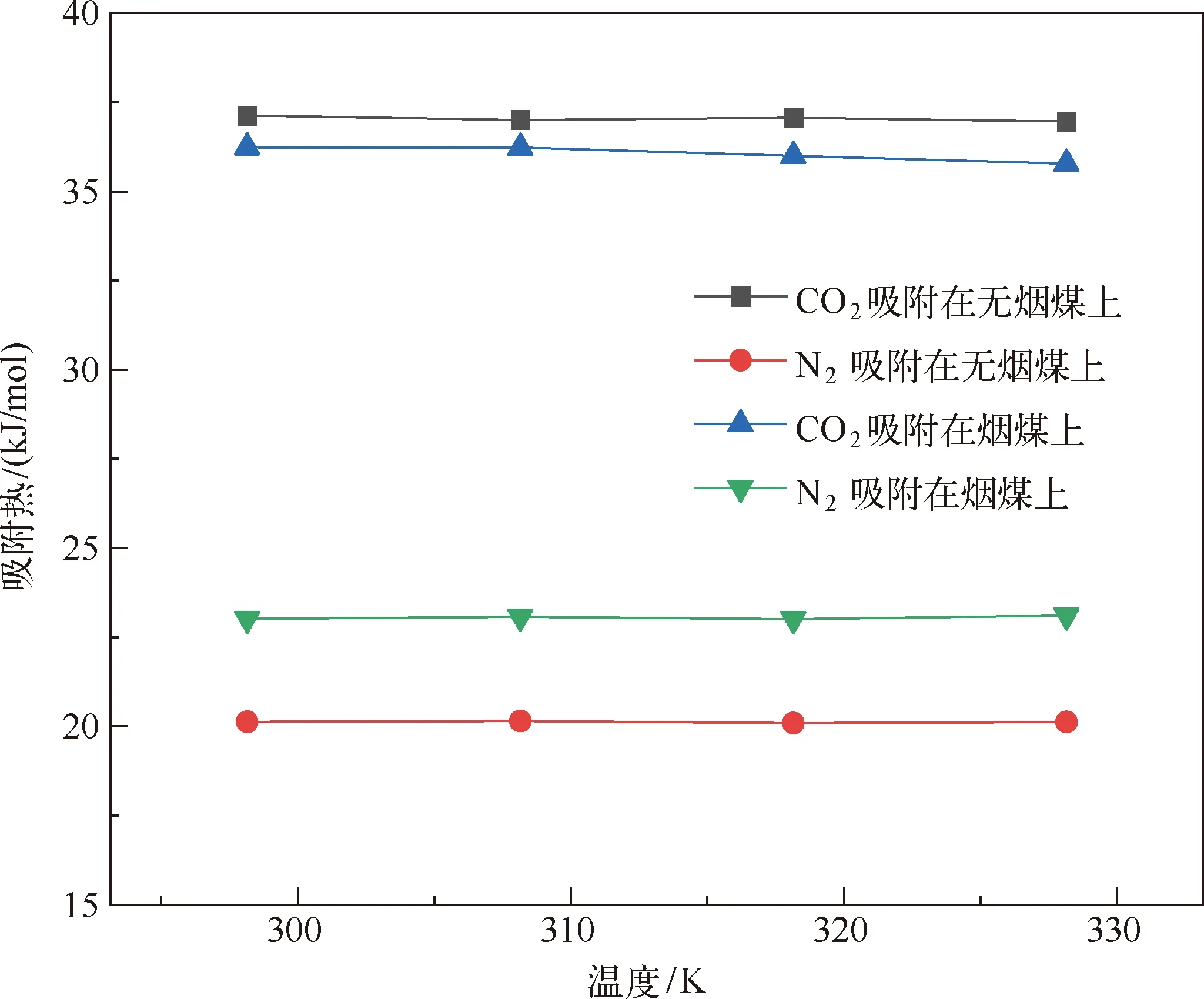

2.4 烟煤与无烟煤中气体的吸附位点

2.5 扩散系数
3 结论
