纤维网格增强混凝土复合材力学性能

胡克旭， 蓝 玥， 李 峣

（同济大学 土木工程学院，上海 200092）

纤维编织网增强混凝土（textile reinforced concrete，TRC）是一种纤维网格增强水泥基复合材料，作为一种新型加固材料用于混凝土结构加固，对原结构自重和截面尺寸影响较小，具有施工简便、适用面广、耐久性好等特点［1］。由于用于加固结构中的TRC复合材往往处于受拉状态，对其力学性能的研究因而主要集中于抗拉性能研究。

目前针对TRC 复合材的力学性能的研究主要是对纤维网格中单股纤维的拉伸性能和对单层纤维网格增强的混凝土复合材试件的拉伸性能研究［2-7］，缺乏系统性地考虑其中纤维股数、网格层数对纤维网格和TRC 复合材受力性能的影响，以及对TRC与被加固结构的混凝土间黏结性能的影响。而实际工程中，纤维网格在TRC复合材中均为多股甚至多层，因此，只针对单股纤维、单层网格的TRC 的试验，忽视了不同股数纤维和不同层数网格间的工作不协调性，从而高估了实际网格的承载能力。由于TRC 复合材中的网格在基体混凝土中不同纤维股间共同工作性能相对纯网格好，致使纯纤维网格的拉伸性能和TRC 中网格的拉伸性能明显不同。另外，国内外目前针对TRC复合材和混凝土间黏结滑移性能的研究发现［8-11］，TRC复合材中的纤维网格层数对其与混凝土间的黏结滑移有明显影响，但缺乏针对工程中常用加固层数进行系统、完整的试验研究。因此，研究不同股数、不同层数纤维网格和TRC的受拉性能，以及TRC与被加固的混凝土间的黏结性能非常必要。

为此，本文结合实际工程中的应用情况，进行了不同纤维股数（1、3、5、8、10股，受试验条件限制未能进行更多股数的试验）和不同网格层数（1、2、3、4层）的纯纤维网格和TRC复合材的拉伸性能试验研究，以及不同网格层数（1、2、3、4层）TRC与混凝土间的黏结滑移性能试验研究，建立了随纤维股数和网格层数变化的纯纤维网格拉伸本构模型、TRC复合材拉伸本构模型和TRC-混凝土界面黏结滑移本构模型，为后续研究和工程应用提供理论依据。

1 纤维网格拉伸性能试验研究

1.1 试验试件

试验采用的纤维网格是目前工程中常用的天津卡本复合材料有限公司生产的CFN 200/200双向碳纤维网格，网格间距双向20 mm，每股纤维理论截面积0.88 mm2，弹性模量240 GPa（厂家提供数据）。网格在生产过程中在其表面通过了浸胶处理以提高碳纤维丝间的共同工作性能。

参考碳纤维复丝的试验方法［13］和国内外有关研究文献，试验纤维网格试件的试验段标距长度为100 mm。为便于试验时对试件的夹持，在纤维网格两端浇筑相应宽度的TRC薄板（试验时夹持长度为200 mm）。网格两端的TRC薄板厚度根据网格层数不同，网格层间距和保护层厚度均为5 mm。试验试件尺寸如图1 所示。宽度有60 mm、100 mm、160 mm 和200 mm4 种，长度均为800 mm。试件制作如图2 所示 ，共8 组，每组3个，分别进行单股单层、3股单层、5股单层、8股单层、10股单层和5股2、3、4层的拉伸试验。

图1 纤维网格拉伸试验试件Fig.1 Fiber mesh tensile test specimen

图2 纤维网格试件制作Fig.2 Pouring of fiber mesh specimens

1.2 试验装置与加载测试

试验装置如图3 所示。试验专门设计了两套钢板夹具以夹持不同尺寸的试件，采用额定拉力为10 t的液压式拉压千斤顶进行加载。试验过程分别通过安装在千斤顶加载端的电子压力传感器和测点位于标段端头的位移计对所加荷载和试件的伸长变形进行采集。电子压力传感器的采集精度为0.069 kN，位移计采集的精度为0.000 5 mm。

图3 试验装置Fig.3 The test device

1.3 试验结果及分析

网格试件的典型破坏形态如图4 所示，断裂位置基本位于测试段中部。拉伸过程中随着荷载不断增大，部分纤维丝先被拉断，随后更多纤维丝被陆续拉断，纤维股伸长，直至完全被拉断。

图4 网格试件破坏形态Fig.4 Failure mode of TRC specimen

网格拉伸试验所得抗拉强度、弹性模量和极限应变结果如表 1 所示。实测不同股数的单层网格试件应力应变曲线如图5 所示，不同层数的5 股网格试件应力应变曲线如图6 所示。图5 和图6 均显示：应力和应变间基本呈线性关系。

表1 纤维网格拉伸结果一览表Tab.1 List of tensile results of fiber mesh

图5 不同股数纤维网格应力应变曲线Fig.5 Stress-strain curve of fiber mesh with different strands

图6 五股试件不同层数纤维网格应力应变曲线Fig.6 Stress-strain curve of 5-strands fiber mesh with different layers

图7 为纤维网格抗拉强度和极限应变随股数变化的情况。随着股数的增多，网格的抗拉强度和极限应变均呈持续下降的趋势；当网格股数为10 股时，其抗拉强度和极限应变分别降低了29.6 %和27.6 %。这主要是因为试件制作时不能保证不同纤维股的张紧程度完全一致，以及纤维网格生产时也不能确保不同纤维股内的纤维丝状态完全一致，随着网格股数增多，其受力均匀性变差，纤维股之间的共同工作状态也变差所致，这也正是本文研究的主要目的。

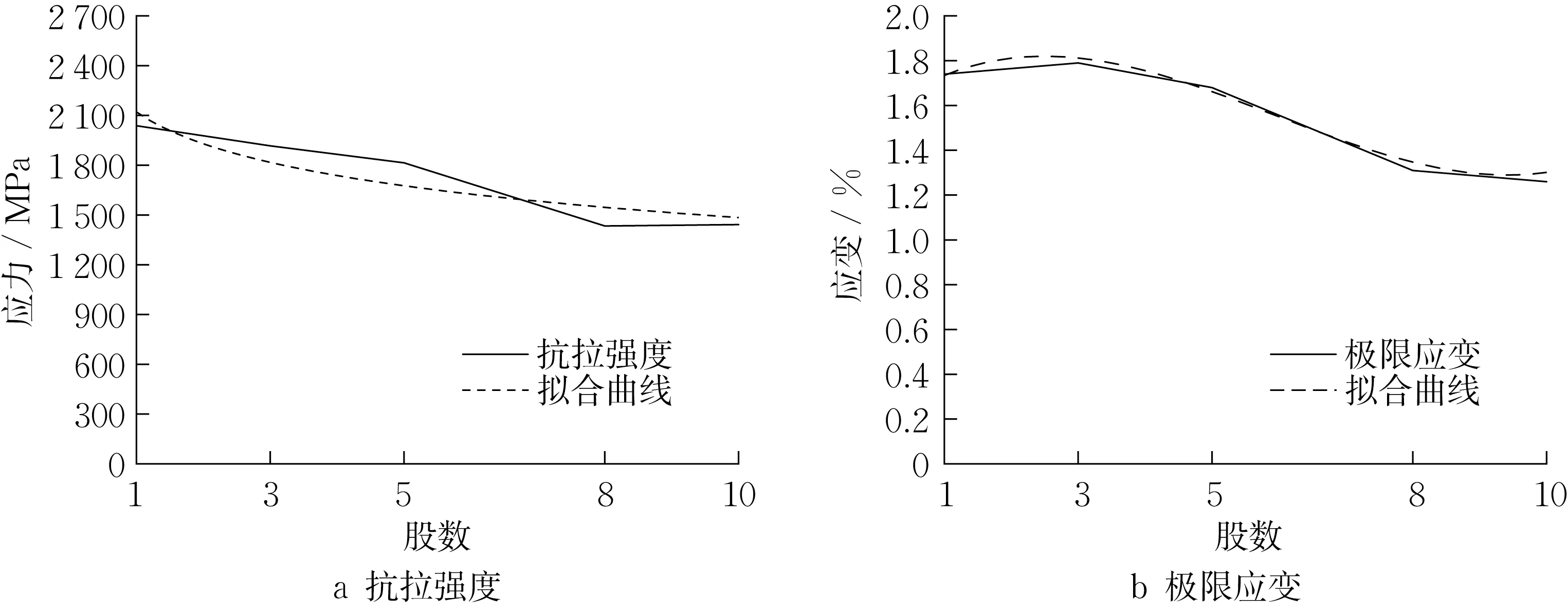
图7 纤维网格力学参数随股数变化关系Fig.7 The relationship between the mechanical parameters of the fiber mesh and the number of strands

图8 为纤维网格抗拉强度和极限应变随层数变化情况。随着层数的增多，网格的抗拉强度也呈现持续下降的趋势，4 层网格较单层网格最大下降约18.3 %。原因也是因为不同网格层的张紧程度不完全一致，随层数增多，不同网格层间共同工作性能变差所致。而不同层数网格的极限应变随网格层数增多略有波动，总体变化趋势并不明显。

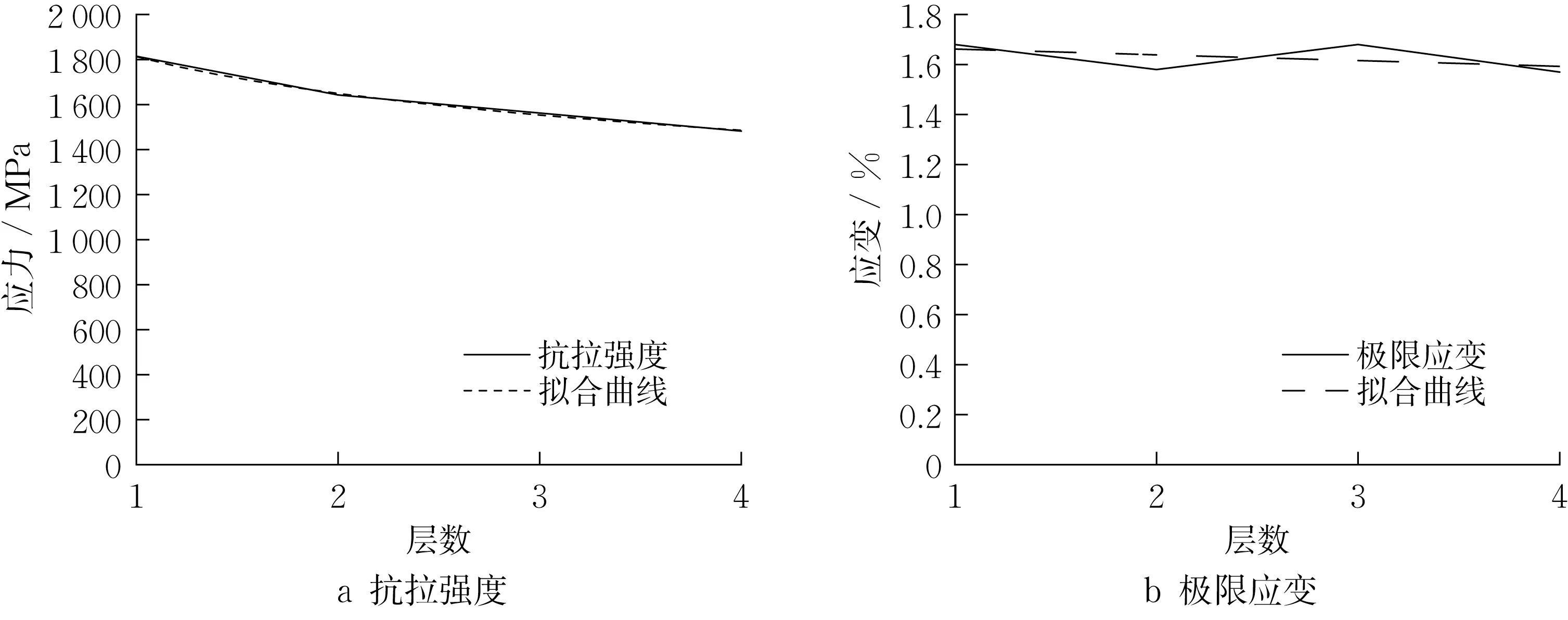
图8 纤维网格力学参数随层数变化关系Fig.8 The relationship between the mechanical parameters of the fiber mesh and the number of layers

1.4 纤维网格拉伸性能本构模型

根据不同股数和不同层数纤维网格拉伸试验所得应力应变曲线，令m为股数、n为层数，以单股单层网格的抗拉强度σfu1、极限应变εfu1为基准，考虑到纤维股数间和网格层数间共同工作性能对抗拉强度和极限应变的影响，引入抗拉强度、极限应变受股数影响系数α1、α2，以及受层数影响系数β1、β2，经拟合整理后得［16］

式（5）即为纤维网格拉伸本构模型，其中σf和εf分别为纤维网格拉伸应力和拉伸应变。使用该模型对不同股数和不同层数纤维网格试验结果的拟合直线分别示于图5 和图6 中，可见，拟合效果良好，基本符合试验情况。

2 TRC复合材拉伸性能试验研究

2.1 试验试件

本试验采用的基体混凝土材料为上海环宇建筑工程材料有限公司生产的秀朴-PM40F聚合物砂浆，实测在自然环境下养护28 d的立方体抗压强度平均值为34.1 MPa，TRC复合材拉伸试验时（龄期98 d）的立方体抗压强度平均值为38.4 MPa［14］。

TRC 复合材拉伸试验试件如图9 所示，试件长均为800 mm，中间试验段长400 mm（两端为夹持端），试件宽度和厚度随纤维网格股数和层数而变化。网格层间距和保护层厚度均为5 mm，故单层试件总厚10 mm，2 层、3 层、4 层试件总厚分别为15 mm、20 mm、25 mm。试件制作如图10 ，共8 组，每组3个，分别进行单股单层、3股单层、5股单层、8股单层、10股单层和5股2、3、4层的拉伸试验。

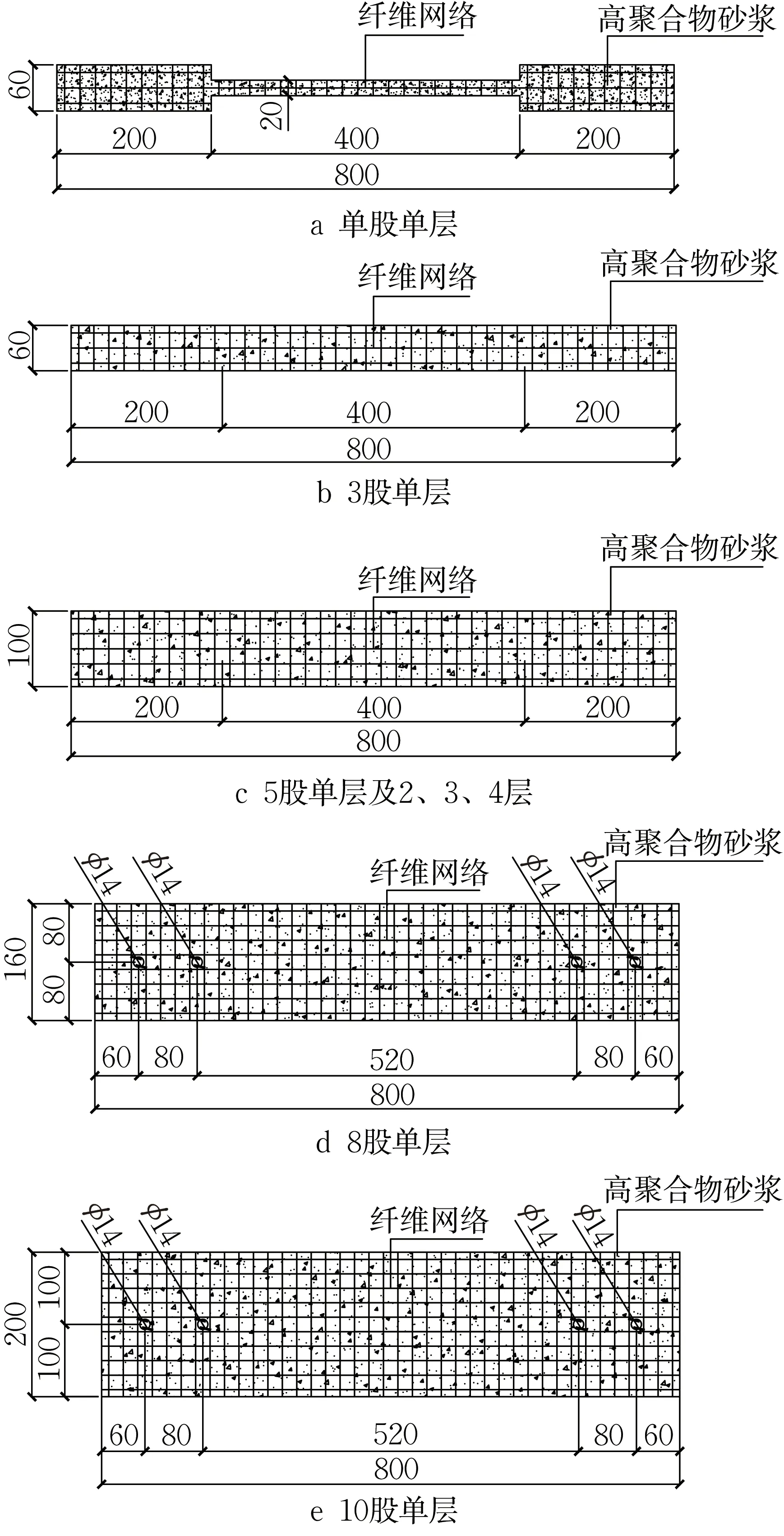
图9 TRC复合材拉伸试件Fig.9 TRC composite tensile test specimen

图10 TRC试件制作过程Fig.10 The pouring process of TRC specimen

2.2 试验装置与加载测试

试验装置与加载制度同前文。试验过程中采用位移计测试TRC试件应变随荷载的变化，测试段长200 mm，位移计布置如图11a、11b。

图11 TRC试件拉伸破坏过程Fig.11 Tensile failure process of TRC specimen

2.3 试验结果

图11 为TRC 薄板试件不同受力阶段的破坏形态。初裂裂缝一般发生在试件中段（图11a ），随着荷载继续增大，试件进入多裂缝开展阶段（图11b ）；继续加载，裂缝宽度不断增大，裂缝处伴随出现基体剥离现象（图11c ）；随后，基体剥离范围沿长度方向不断发展，最后网格被拉断（图11d ）。

表2 为TRC薄板试件拉伸试验所得开裂应力、抗拉强度和极限应变结果汇总。其中“开裂应力”和“TRC 抗拉强度”为相应荷载除以TRC 薄板截面积所得，是TRC复合材的名义应力和抗拉强度；而“网格抗拉强度”为极限荷载除以网格截面积所得，由于达到极限承载力时基体材料早已开裂并退出工作，TRC 复合材的抗拉强度实际上就是网格的抗拉强度。对比表2 和表1 可以看出，TRC中的网格抗拉强度明显高于相同条件下（股数、层数）纯网格的抗拉强度，这主要是由于TRC中的砂浆基体为网格提供了较好的共同工作基础，使TRC中的不同纤维股之间能更好地协调受力。

表2 TRC试件拉伸结果一览表Tab.2 List of tensile results of TRC specimens

试验所得单层不同网格股数的TRC试件应力应变曲线见图12，5股不同网格层数的TRC试件应力应变曲线见图13。如图12～图13所示，随着应力增加，应变不断增大，二者之间不再呈线性关系。

图12 不同股数TRC应力应变曲线Fig.12 Stress-strain curve of TRC with different strands

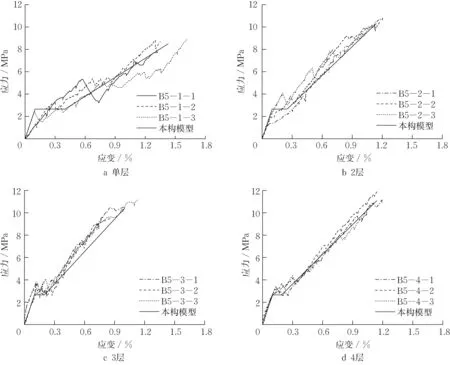
图13 5股试件不同层数纤维网格应力应变曲线Fig.13 Stress-strain curve of 5- strands TRC with different layers

图14 为TRC抗拉强度和极限应变随纤维股数变化的情况。随着股数的增多，TRC抗拉强度呈下降趋势；当网格股数为8股时，其抗拉强度较单股时下降了19.77 %；但与图7a 相比，下降幅度明显减小。前者是因为随着股数增多，其受力均匀性变差，纤维股的共同工作状态也变差所致，后者则是因为TRC 中的砂浆基体为网格提供了一定的共同工作基础，使TRC中的不同纤维股之间较纯网格能更好地协调受力。根据图14b ，随着股数的增多，TRC的极限应变基本保持在1.2 %～1.5 %之间，无明显变化趋势。

图14 TRC拉伸力学参数随股数变化关系Fig.14 TRC tensile mechanical parameters change with the number of strands

图15 为TRC抗拉强度、TRC中纤维网格抗拉强度和TRC极限应变随网格层数的变化情况。随着层数不断增多，TRC抗拉强度呈上升趋势，4层网格的TRC较单层时约增大23.29 %；TRC中网格的抗拉强度呈下降趋势，4层网格较单层时约下降18.52 %。前者是因为随着网格增多，增大了TRC的含筋率，使其抗拉强度提高；后者则是因为网格层数越多，网格层间的共同工作性能越差，导致其抗拉强度越低。但相比于图8a 的纯网格情况，网格层数对抗拉强度的影响幅度基本相同，说明TRC中的基体砂浆对不同网格层间提供的共同工作性能不明显。

图15 TRC拉伸力学参数随层数变化关系Fig.15 TRC tensile mechanical parameters change with the number of layers

根据图15c ，随着网格层数的增多，TRC的极限应变先是下降，超过3 层后则是增大。极限应变反映了TRC达到极限承载力时的变形大小，随着网格层数增多，TRC 的含筋率增大，TRC 受拉时网格的贡献也增大，而由于纤维网格的受拉弹性模型明显高于基体砂浆材料，因此，其极限应变也随之下降；至于大于3 层后TRC 极限应变反而增大，主要是由于随着网格层数增多，网格间共同工作性能更差，导致受力时网格纤维拉断过程变长，应变增大。

2.4 TRC拉伸本构模型

基于ACK 理论（Aveston-Cooper-Kelly）模拟脆性复合材料的多裂缝特征已经相当成熟［6］，本文使用ACK 理论推导TRC 拉伸本构模型，并做以下假定：①拉伸过程中TRC 截面满足平截面假定；②基体与纤维束之间的平均黏结应力为常数；③纤维束仅受外荷载方向的力，不考虑其横向收缩变形。基于此，ACK 理论可将TRC 单轴拉伸应力—应变曲线简化为三段直线，如图16 所示。

图16 中σtu1和εtu1分别为第一折点应力和应变，即开裂应力和开裂应变；Etu1为TRC 薄板试件第一阶段的弹性模量；εtu2为第二阶段结束时的应变，这一阶段假定为水平段，试件的应力无变化；σtu，u为极限应力，εtu，u为极限应变，Etu3为TRC 薄板试件第三阶段的弹性模量，即稳定裂缝阶段的弹性模量。

根据ACK 理论，TRC 复合材拉伸试件第一阶段符合复合材料混合定律，此时复合材料的刚度与纤维和基体的弹性模量及体积率有关［16］，即

式中：Etu1为TRC 复合材料的弹性模量，Em和Vm分别是基体材料的弹性模量和体积率，Ef和Vf分别为纤维网格的弹性模量和体积率。

第一阶段结束后，试件会达到开裂应力σtu1，其主要受基材的极限抗拉强度σmu控制：

当基体混凝土开裂后，未开裂部分通过纤维网格与基体材料间的黏结力将荷载由纤维网格传递给基体材料，其有效黏结长度δ可根据应力平衡得到，即

式中：Am为基体体积；Cf为单股径向纤维周长；n为纤维总股数；τ为纤维束和基体混凝土之间的平均黏结应力。在多裂缝阶段，裂缝的间距在δ和2δ之间。根据文献［7］，裂缝间距的平均值可取为1.337倍的δ，因此，第二阶段结束时的应变εtu2为

当试件应变达到εtu2时，多裂缝阶段结束，试件开始进入第三阶段即稳定裂缝阶段，在此阶段主要由纤维束承担应力，试件的刚度计算如下：

当纤维网格完全断裂时，TRC 复合材的极限应变取决于纤维网格材料力学性能，其表达式如下：

所以，TRC复合材拉伸本构模型表达式如下：

式（12）的模型中，纤维网格相关力学参数按纤维网格拉伸试验中结果采用，基体混凝土弹性模量Em参考课题组先前试验结果［12］取25.3 GPa，基体混凝土抗拉强度σmu根据文献［15］，可通过抗压立方体抗压强度进行换算，取

式（12）对不同股数试件和不同层数试件进行拟合的结果见图12 和图13 ，各工况下拟合情况基本良好。

3 TRC-混凝土黏结滑移性能试验研究

3.1 试验试件

试验采用的基体材料和碳纤维网格同前述试验。为研究TRC复合材与被加固的混凝土构件表面间的黏结滑移性能，本文采用图17a 所示中心穿有同一根Ф 20钢筋的成对混凝土试块（整体浇筑后再切开）进行拉伸剪切试验。混凝土试块尺寸300×150×150 mm，实测28 d标准立方体试块的抗压强度平均值为36.5 MPa，黏结滑移试验时（龄期440 d）立方体试块抗压强度平均值为41.1 MPa。TRC施工前先对混凝土试块表面进行凿毛处理（图17c ），实测平均凿毛深度为3.68 mm，经对试块周边进行保护处理，有效黏结范围为126×128 mm（图17d ）。为确保试验时发生黏结面破坏（而不是网格被拉断），试验前经切割后预留的每侧有效黏结长度为30 mm。TRC内网格层间距和保护层厚度均为5 mm，试件制作情况如图18 所示，为防止TRC层产生收缩裂缝，基体砂浆中掺加了一定量的膨胀剂和一定比例的短纤维。试验试件共4组，每组3个，分别进行单层、2层、3层、4层网格的TRC与混凝土黏结滑移试验。

图18 TRC-混凝土黏结滑移试件制作过程Fig.18 The process of making TRC-concrete bondslip specimens

3.2 试验装置与加载测试

试验装置与加载同前文，位移测量采数字图像相关法（digital image correlation，简称DIC 技术），通过定时拍照并处理照片中同一个点相对位置的变化来计算位移变化，如图19 所示。同时，还在试件上、下两端安装了位移计以测量试件总变形量。

图19 TRC-混凝土黏结滑移试件位移测试Fig.19 Displacement measurement of TRC-concrete bond-slip specimens

3.3 试验结果

TRC与混凝土间的黏结滑移试件在外荷载作用下主要产生了3种破坏形态：基体与纤维网格之间的剥离破坏（I型）、TRC与混凝土间黏结面破坏（IIa型）和黏结面处混凝土破坏（IIb型），如图20 所示。表 3 为TRC-混凝土黏结滑移试验结果汇总，试验所得不同加固层数的各试件黏结滑移曲线如图21 所示，二者基本呈线性关系。单层和2层网格时，破坏形态以I型为主，3层及以上时则主要发生IIa和IIb型破坏，说明随着网格层数增加，TRC本身抗拉强度提高，相对而言TRC与混凝土间的黏结面变弱。

图20 TRC-混凝土黏结滑移破坏形态Fig.20 TRC-Concrete bond-slip failure mode

表3 TRC-混凝土黏结滑移试验结果一览表Tab.3 List of TRC-concrete bond-slip test results

图21 不同加固层数TRC-混凝土黏结滑移曲线Fig.21 TRC-concrete bond-slip curve for different reinforcement layers

图22 为TRC-混凝土黏结强度和极限滑移量随网格层数的变化情况。随着网格层数增多，黏结强度和极限滑移量均呈上升趋势，4层网格时的黏结强度相较于单层网格增长了63 %，极限滑移量增长了71 %。TRC-混凝土间的黏结滑移包括两部分：一是TRC内部纤维网格与基体材料间的黏结滑移；二是TRC与混凝土界面间的黏结滑移。其中黏结强度受二者中较弱者控制，随着网格层数增多，TRC抗拉强度不断提高，TRC中网格与基体间的抗剥离能力也相应提高，界面行为则表现为由Ⅰ型向Ⅱ型转化。理论上，TRC与混凝土界面的黏结强度主要与基体材料和混凝土材料强度及界面粗糙度有关，因此可以预测，网格层数达到一定值后，界面黏结强度应该趋于稳定，但本文试验工况有限，未获得这一网格层数值，有待后续进一步研究。而TRC-混凝土间的极限滑移量是由纤维网格与基体材料间的滑移量和TRC与混凝土间的滑移量两部分组成的，其中前者的贡献更大，因此，随着网格层数增多，网格与基体材料间的滑移量增大，表现为图22b 所示的TRC-混凝土间的极限滑移量也不断增大。

图22 黏结强度和滑移量随加固层数变化关系Fig.22 The relationship between bond-slip parameters and the number of reinforcement layers

3.4 TRC-混凝土黏结滑移本构模型

根据不同层数纤维网格试件黏结滑移试验所得黏结应力-相对滑移量曲线（见图21 ），令n为层数，以单层网格时的黏结强度τm1、极限滑移量sm1为基准进行无量纲化，同时考虑到网格层数对黏结强度和极限滑移量的影响，引入黏结强度、极限滑移量受层数影响系数b1、b2可得［16］

式（16）即为TRC-混凝土黏结滑移本构模型，用其对不同网格层数的TRC进行拟合的结果示于图21中，可以看出拟合曲线与试验结果基本吻合。

4 结论

本文通过不同股数和不同层数纤维网格拉伸试验、不同股数和不同层数纤维网格的TRC复合材拉伸试验、不同层数纤维网格的TRC-混凝土黏结滑移试验，研究了纤维股数和网格层数对抗拉性能和界面黏结性能的影响，主要结论和成果如下：

（1）随着纤维股数和网格层数的增多，纤维网格的抗拉强度均呈持续下降的趋势，主要是因为不同纤维股和不同网格层间不能很好的共同工作所致，而且纤维股数和网格层数越多，共同工作性能越差。同样，随着纤维股数和网格层数的增多，TRC复合材的抗拉强度也呈持续下降的趋势，但由于基体砂浆材料的存在，不同纤维股和不同网格层间的共同工作性能得到改善，表现为TRC抗拉强度的下降幅度明显低于纤维网格，TRC中纤维网格的抗拉强度也明显高于纯网格。

（2）随着网格层数增多，TRC-混凝土黏结强度和极限滑移量均呈明显上升趋势，4层网格时黏结强度和极限滑移量相较于单层网格分别增长了63 %和71 %。TRC-混凝土黏结破坏形态基本有两种：TRC内部基体与纤维网格之间的剥离破坏（I型）和TRC与混凝土间的黏结面破坏（Ⅱ型），随着网格层数增多，TRC中网格与基体间的抗剥离能力相应提高，界面行为表现为由Ⅰ型向Ⅱ型转化，极限滑移量也相应增大。

（3）通过试验研究，建立了随纤维股数和网格层数变化的纤维网格拉伸本构模型、TRC复合材受拉本构模型和TRC-混凝土黏结滑移本构模型，为后续研究和工程应用提供了理论依据。

作者贡献声明：

胡克旭：制定研究计划，试验方案设计、参与试验过程和试验结果分析；

蓝玥：参与试验过程，试验结果分析及论文撰写；

李峣：试验试件设计与制作，负责试验和试验数据处理、试验结果分析及理论分析。