基于XGBoost的管道防腐层裂纹损伤识别算法研究

吕瑞宏，王春云，赵艺伟，王晨丽

(沈阳工业大学 信息科学与工程学院，沈阳 110870)

0 引言

由于土壤腐蚀和自然环境的影响，长输埋地管道防腐层产生的裂纹易使管道金属层出现损伤，从而导致管道泄漏、断裂甚至爆炸，因此对管道防腐层进行裂纹损伤识别具有重要意义[1-2]。管道防腐层损伤检测是保障管道安全运输的重要研究内容，利用超声导波技术检测管道防腐层缺陷具有明显优势[3-4]。

目前，李强林等证明了超声导波检测技术可用于埋地管道的快速检测[5]；张广纯等应用超声导波检测技术识别了铝板缺陷的类型、大小及位置信息[6]；杨辰等将位移值和固有频率值相互融合成一种新的损伤特征向量矩阵，该方法可以有效地对损伤位置以及程度进行识别和评估[7]；刘文光等[8]提出以固有频率为损伤特征向量的裂缝识别方式；王红君等提出一种基于集合经验模态分解(EEMD，ensemble empirical mode decomposition)小波阈值去噪和布谷鸟算法优化BP神经网络的方法，实现了风电机组齿轮箱中故障的诊断[9]；杨晓晖等提出基于多粒度级联孤立森林(IForest，isolation forest)的检测模型，提高了在高维数据中异常值检测的精确度[10]；吴小姣等[11]将缺失森林(MF，miss forest)填补法与贝叶斯线性回归法、蒙特卡洛多重填补法、K邻近填补法进行对比，结果表明缺失森林在缺失数据中填补优势最大；李仙琳[12]等利用核主成分分析(KPCA，kernel principal components analysis)算法对钻井各参数进行信息整合，结果表明基于KPCA优化的模型较其他模型具有较高的溢流诊断率及模型泛化能力；夏田等[13]采用小波包分解与梯度提升树(GBDT，gradient boosting decision tree)算法相结合的方法对轴承故障进行损伤识别，结果表明此方法在轴承损伤识别方面表现优异；李超[14]采用极端梯度提升(XGBoost，extreme gradient boosting)算法构建爆管风险评估模型，结果证明基于XGBoost的管道爆管风险评估模型具有较高的精准性与稳定度。

基于以上研究，针对管道防腐层结构的固有频率值对于不同损伤长度的裂纹的敏感程度不同，本文以频域特征固有频率值作为管道防腐层裂纹损伤识别的特征向量，利用孤立森林和缺失森林对频域特征值进行异常检测和数据补全，并应用KPCA对得到的损伤数据库进行特征降维，获取优化后的裂纹损伤数据集，构建基于XGBoost的管道防腐层裂纹损伤识别模型，实现裂纹损伤长度的判定，并通过有限元仿真与现场实验验证其有效性。

1 裂纹损伤数据系统的构建与优化

1.1 裂纹损伤数据系统的构建

在管道防腐层裂纹损伤识别中，采集到的原始裂纹损伤信号s(t)是非线性的，设定s(t)为：

s(t)=x(t)+n(t)

(1)

式中，x(t)为裂纹损伤信号，n(t)为噪声信号。为了从混叠的s(t)中提取裂纹损伤信息，消除噪声的干扰，本文选用EEMD方法对s(t)进行去噪分解，在EEMD中引入噪声辅助信号分析，可以有效解决经验模态分解(EMD，empirical mode decomposition)中可能出现的模态混叠现象。EMD是将原始信号X(t)分解为一系列本征模态函数mi(t)和一个残余量rN(t)之和，表达式为：

(2)

式中，mi(t)为本征模态函数，rN(t)为残余量。

EEMD在s(t)中添加白噪声辅助分析，将s(t)分解为多个尺度分量之后继续进行总体平均运算，去除白噪声的干扰，获取最终的信号分解量[15]。基本的实施流程如下：首先选择集总平均次数N和标准高斯白噪声的标准差σ生成均值为0、标准差为σstd(x)的高斯白噪声并加入到s(t)中，然后对合成信号进行EMD处理并重复上述步骤共N次，最后取N次分解得到的IMF分量的平均作为EEMD的IMF分量。

对采集的s(t)进行EEMD时频分析，得到10个IMF分量M1(t)，…，M10(t)和1个残余分量R1(t)，由于前六阶IMF分量构成了s(t)的主要瞬时信号，后四阶IMF分量的能量分布较小，其对于s(t)的影响可忽略不计，因此本文只取前6个IMF分量M1(t)，…，M6(t)进行分析。

对上述经过EEMD时频分析处理后获得的M1(t)，…，M6(t)进行FFT频域特征处理，提取裂纹损伤信号的频域特征值Ci(k)，i=1，2，…，6，公式如式(3)所示：

FFT[ac1(t)+bc2(t)+…]=aC1(k)+bC2(k)+…

(3)

式中，a与b均为常数，通过FFT计算得到各个分量的频域特征C1(k)，…，C6(k)构成管道防腐层裂纹损伤数据集S，表达式为：

S={C1，C2，C3，C4，C5，C6}

(4)

其中：C1，…，C6为裂纹损伤信号的六阶频域特征值。

1.2 基于孤立森林的损伤数据异常检测

在对管道防腐层双层结构进行健康检测的过程中，不可避免地会受到环境影响或人为因素的干扰，可能导致采集到的管道损伤数据中存在异常值。管道损伤数据集中的异常值会影响后续进行管道损伤的类型与尺寸识别，为减小管道损伤检测的误差，需要对管道损伤数据集进行异常值识别，检测出损伤数据集中的异常值并进行剔除。

孤立森林(IForest)异常值检测算法的基学习器是决策树[16]，IForest的核心是将S中的异常值孤立出来[17]，该算法在损伤数据异常识别中性能表现优异。IForest定义异常样本为离群点，离群点离分布密集的正常样本的距离较远，而且离群样本通常呈现稀疏分布。IForset针对异常值的孤立方法如图1所示，对S进行多次样本分割，因异常点分布稀疏的特性，只需要极少次的分割就能够将其检测出来。

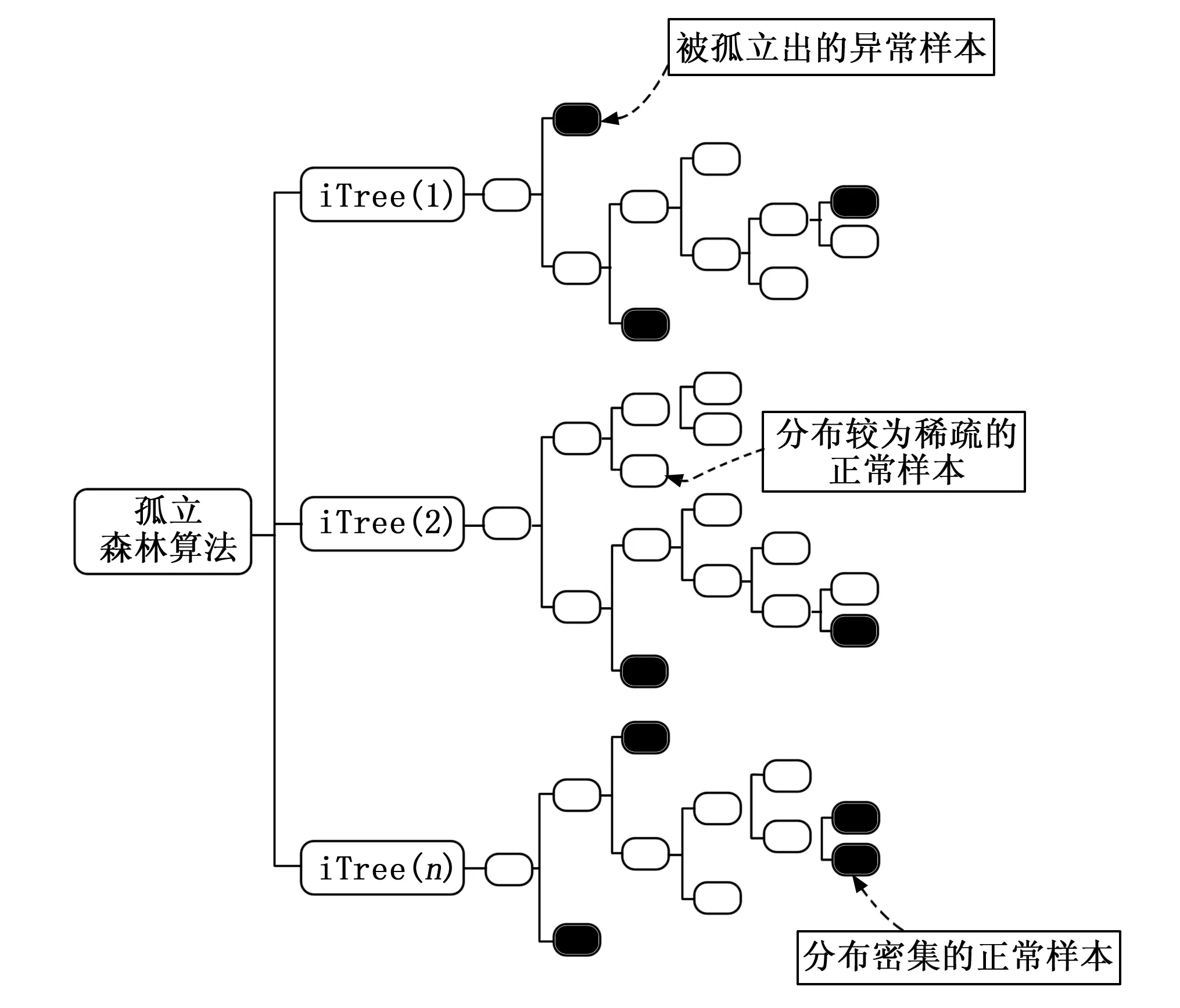
图1 运用孤立森林进行异常检测

利用IForest进行异常检测时，首先对S随机抽样并进行训练，设定孤立树为100棵，异常值比例为0.05，此时S为6维数据。应用IForest对S进行异常检测可视化时，由于结果图受2维平面的限制，因此选择S中的两维特征进行可视化操作，结果图如图2所示。

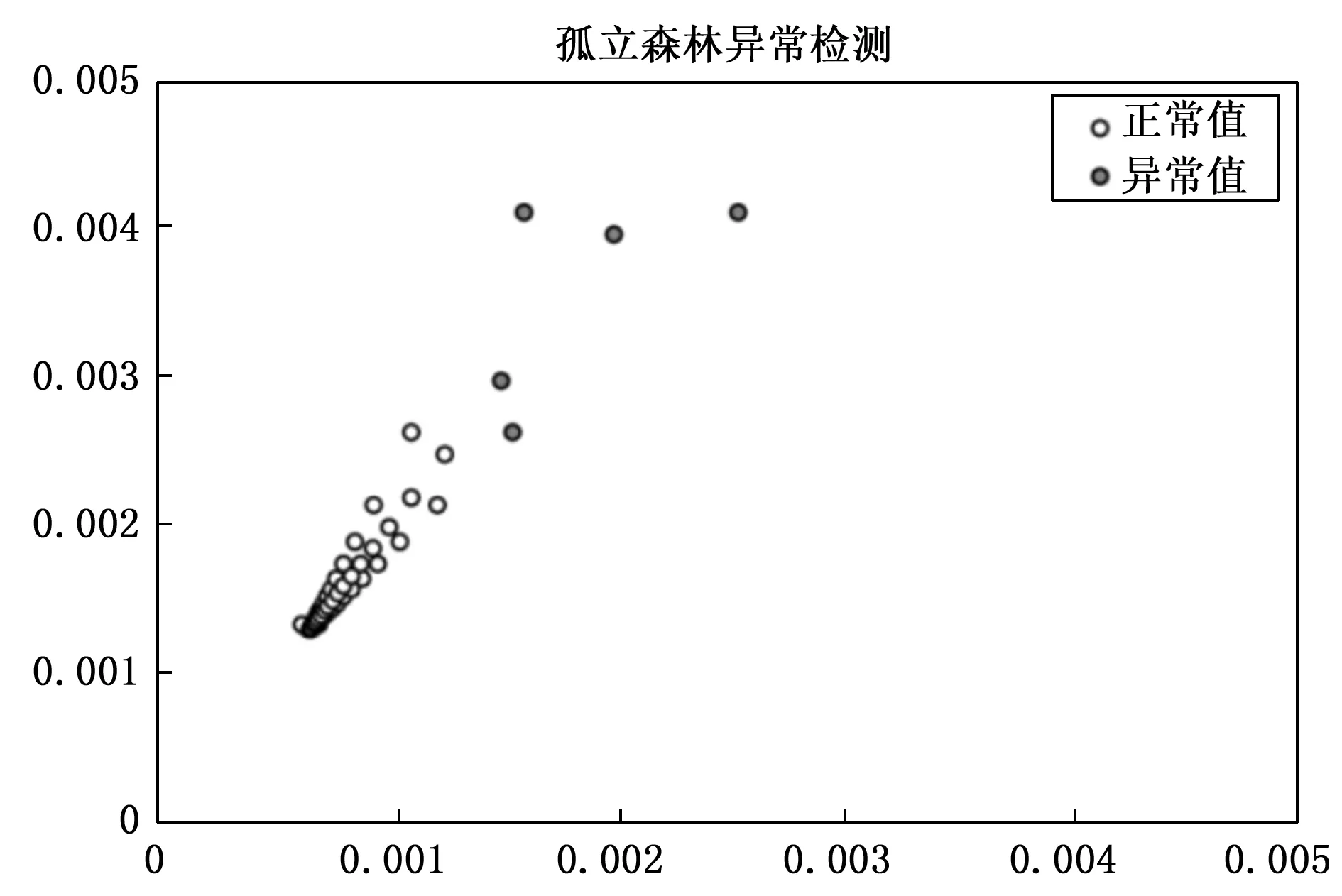
图2 裂纹损伤数据集异常检测可视化

从统计学的角度分析，裂纹损伤数据中的正常值分布在稀疏区域的机率很小，因此能够确定分布在稀疏区域的裂纹损伤数据为异常值，应用IForest将S中的异常值识别并剔除后构建新的裂纹损伤数据集X。

1.3 基于缺失森林的损伤数据补全

由于应用IForest对S进行异常值检测后剔除异常数据会导致数据缺失，因此需要通过数据补全的方法补全X。传统的数据补全方式有均值填补、中位数填补以及众数填补等，而采用传统的填补方式来补全X与S相比会产生较大的误差，故本文选择缺失森林(MF)算法对X进行数据补全。MF算法弥补了传统的数据补全方法的不足，MF是基于随机森林的一种较为常用的数据补全算法，首先通过完整部分的X训练出随机森林预测模型，然后对X中缺失的损伤数据进行预测，最后通过不断迭代来补全X中全部缺失的损伤数据。在缺失森林算法参数的设定中，决策树数量为500，选择有放回采样，并行决策树数量为1。

裂纹损伤数据集X的数据补全过程如下：

1)利用传统填补方式，例如均值填补、众数填补对X进行填补；

2)X的缺失列按缺失率进行排序，缺失列的指标集记为M；

3)当不满足停止准则γ时：

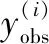
(4)依次对M中缺失数据进行数据补全，直到满足停止准则γ或已达到最大的迭代次数。

4)最终对X进行数据补全，构建补全后的裂纹损伤数据集为D。

1.4 基于KPCA的损伤数据特征降维

为了更全面反映裂纹损伤信号中包含的信息，需要尽可能多的采集裂纹特征参数，然而由于原始特征参数的维数过大和相关性会为后续进行裂纹损伤长度识别造成影响，因此本文利用KPCA对裂纹损伤数据集D进行有效性分析，筛选出最能表征不同缺陷差异的裂纹特征参数，并将高维原始特征空间降维到低维特征空间。

KPCA是一种基于线性PCA的非线性扩展降维方法，KPCA原理是将D的样本空间映射到更高维度的空间，再进行PCA处理。假设裂纹损伤样本d1，d2…dM，{di}表示裂纹损伤样本空间，通过KPCA的映射为Φ，公式定义：

Φ=Rd′→F
daξ=Φ(d)

(5)

样本空间d到F的映射通过核函数实现，由核函数映射的样本空间满足中心化条件为：

(6)

则特征空间中的协方差矩阵为：

(7)

得到C的特征值λ(λ≥0)和特征向量v为：

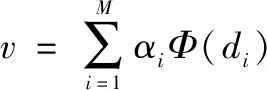
(8)

则有：

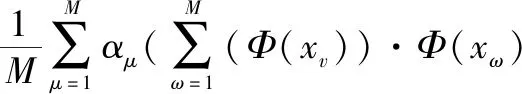
(9)

其中：v=1，2，…，M。定义M×M维矩阵K：

Kμν=(Φ(dμ)·Φ(dv))

(10)

则式(9)简化为：

MλKα=K2α

(11)

由此可得λ和v，对于裂纹损伤样本在特征向量空间Vk中映射为：

(12)

将核函数替换内积，则有：

(13)

当式(6)不成立时，需调整核矩阵为：

(14)

本文采用KPCA方法对裂纹损伤数据集D进行特征提取，处理过程如下：

首先获取n个指标，其中每个指标均有m个裂纹损伤样本，记为m×n维裂纹损伤数据矩阵，然后选择高斯径向核函数并计算核矩阵K，通过公式(14)来调整核矩阵并计算裂纹损伤数据的特征值λ1，…λn以及对应的特征向量v1，…vn；将特征值进行排序，对损伤特征向量正交化得到α1，…αn，计算损伤特征值贡献度B1，…Bn并对贡献度低的维度进行降维处理；最后通过K计算裂纹损伤特征向量投影Y=KL·α，其中α=(α1，…，αt)，Y即为经过KPCA降维优化后的裂纹损伤数据集。

裂纹损伤数据集D中包含6维频域特征向量，对其进行KPCA特征降维，计算裂纹各个损伤特征的特征值和贡献度分别如图3和图4所示，其中PC1到PC6对应D中的6维裂纹损伤特征。

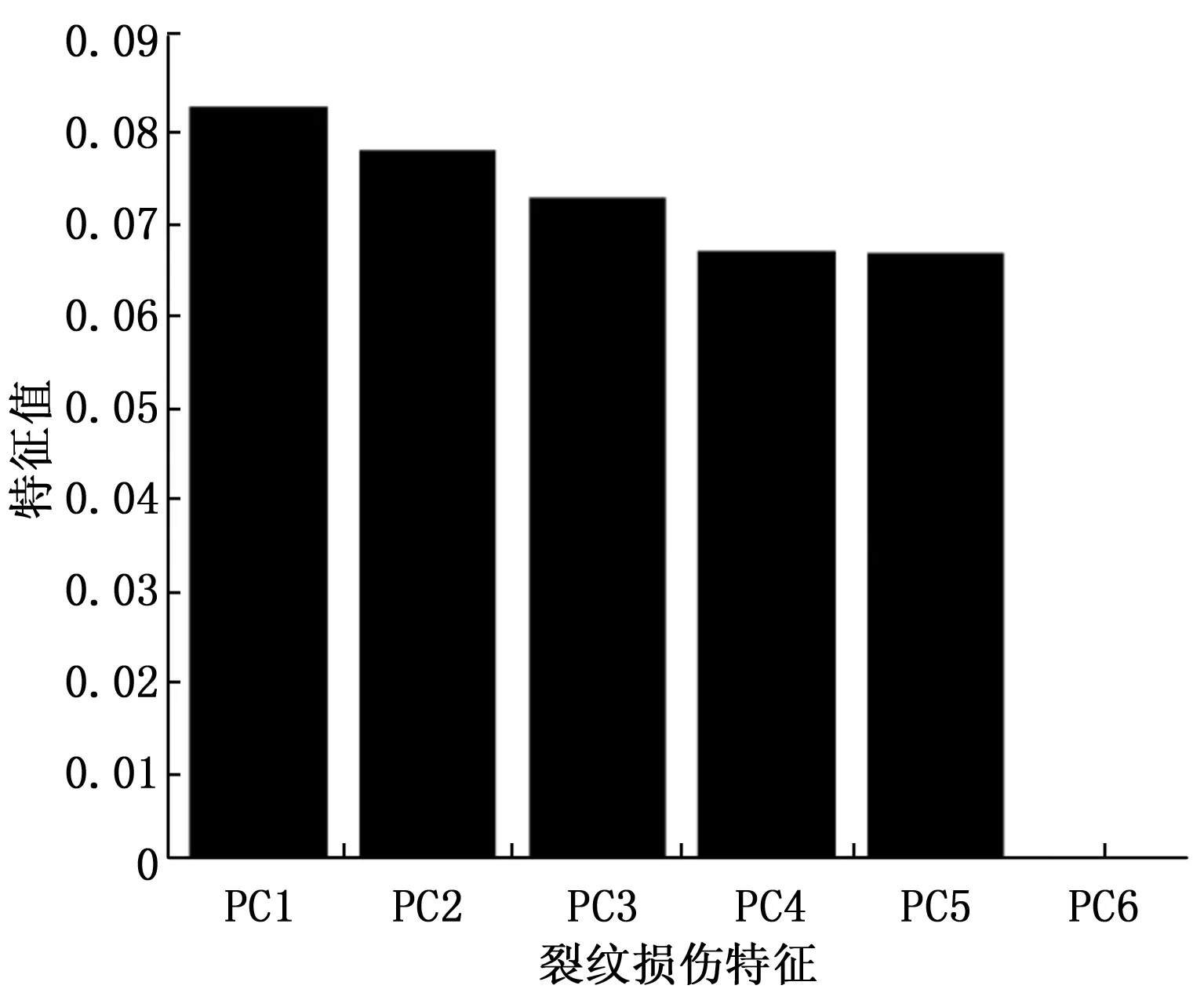
图3 各损伤特征的特征值

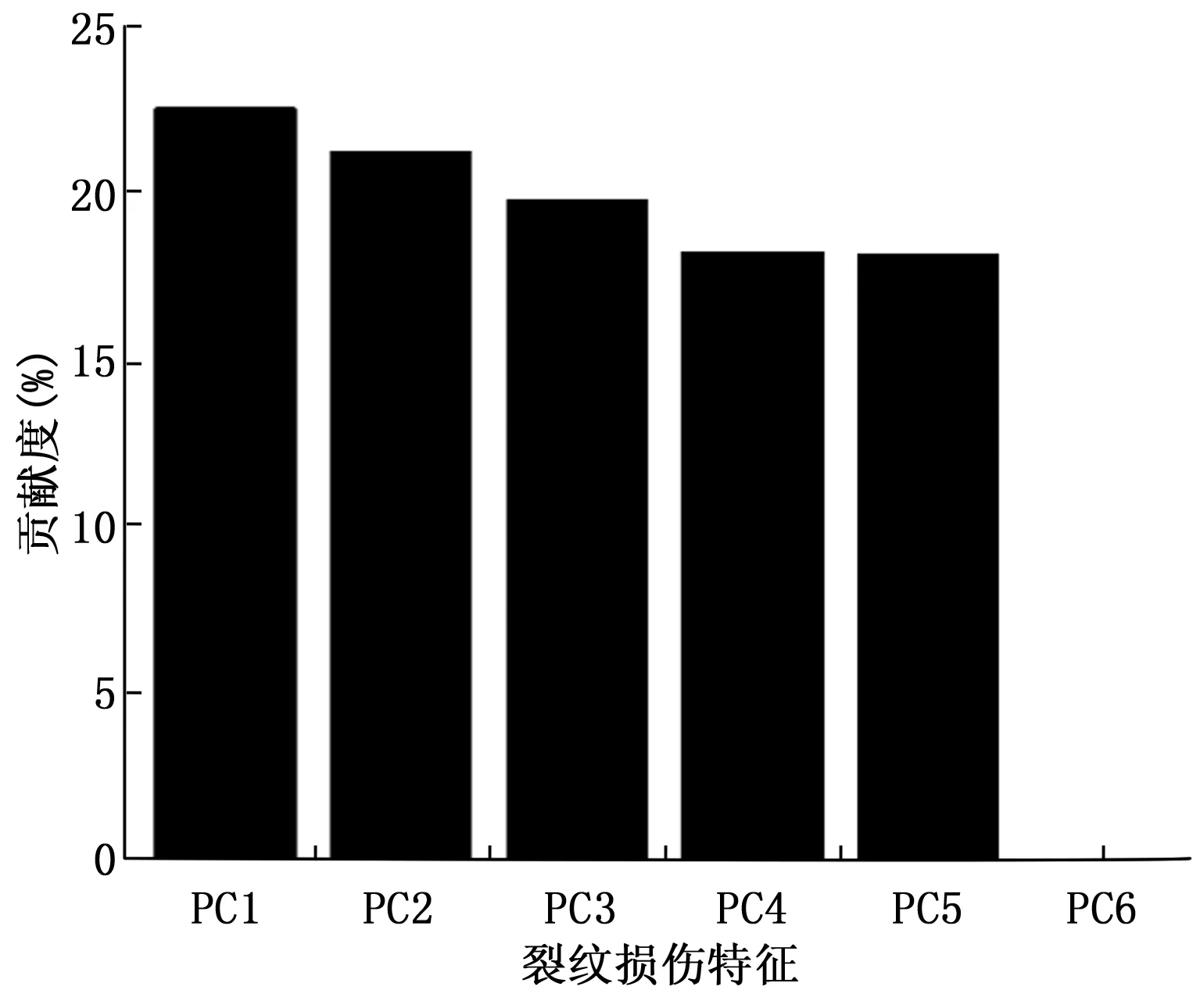
图4 各损伤特征的贡献率

由图3可知，PC6的特征值可以忽略不计，由图4可知，PC1到PC5的贡献率累加能够覆盖99%的裂纹损伤特征信息，所以本文选取前5阶裂纹损伤特征向量构建新的裂纹损伤数据集Y={Y1，…，Y5}。

2 基于XGBoost的裂纹损伤识别

由于上述构建的裂纹损伤数据集Y是非线性的，因此本文选择非线性逼近能力优秀、预测准确率高且训练时间短的极端梯度提升树(XGBoost)算法进行裂纹损伤长度识别。XGBoost算法是在GBDT算法上进行优化，通过多棵决策树来组合拟合上次回归预测反馈的残差，是一种基于串行的集成学习算法[18-21]。

XGBoost的基学习器选择分类回归树(CART)，模型公式如下：

(15)

其中：Ψ={f(x)=wq(x)}(q：Rm→T，w∈RT)，q表示分类回归树映射损伤样本到叶节点的分数，wq(x)表示所以分类回归树映射分数的集合，T代表分类回归树叶节点的数量，则模型的目标函数为：

(16)

(17)

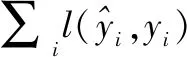
决策树预测的残差值被生成的决策树拟合，当t棵决策树生成后，得到的公式为：

(18)

将目标函数记为：

(19)

提取第t棵分类回归树的预测值进行优化，可以使用二阶泰勒展开近似表示为：

(20)

公式(20)中gi和hi分别为i第个样本预测值的一阶梯度和二阶梯度：

(21)

(22)

移除ft(xi)无关项，定义Ij={i|q(xi)=j}为第t棵决策树中第j个叶子节点所在的损伤样本，对损失函数进行简化得到：

(23)

计算得到第t次迭代中损失函数极值点的值为：

(24)

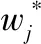
(25)

由于原始裂纹损伤信号s(t)是非线性的，因此采用EEMD方法对s(t)进行去噪分解，得到多个IMF分量，IMF分量中同时包含了裂纹损伤信息和噪声信息，应用FFT提取频域特征固有频率值并构建裂纹损伤数据集S，利用S作为模型输入直接进行裂纹长度识别时会导致数据精准度下降从而产生误判，因此需要对S进行数据优化。由于S的复杂程度较高，采集过程又存在环境影响和人工失误等因素，可能会造成S中存在异常值。为了消除异常值，采用IForest算法对S进行异常值检测。通过IForest识别并剔除异常值后，构建的裂纹损伤数据集X中存在缺失值，采用缺失森林算法对X进行数据补全，构建裂纹损伤数据集D。KPCA能够优化裂纹损伤数据，提取主要损伤特征向量，得到5阶裂纹损伤固有频率值Y作为裂纹损伤长度识别的特征向量。因此，本文提出了IF、MF、KPCA优化XGBoost的管道防腐层裂纹损伤识别算法，由以上分析提出基于XGBoost的裂纹损伤长度识别模型的流程图如图5所示。

图5 裂纹损伤长度识别模型流程图

3 含裂纹的管道防腐层有限元仿真

当管道的半径足够大时，可将管道防腐层双层结构看作管道-防腐层双层板状结构来进行研究，管道防腐层双层结构微体元模型如图6所示，其中钢制管道内径R1、外径R2，防腐层厚度为hv=(R-R2)，钢管厚度为hE=(R2-R1)，取钢制管道中厚度为R-R1、宽度为d、体积为V的单元体可看作宽度为d的钢板-防腐层双层板状结构。

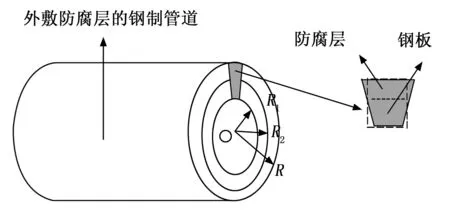
图6 管道防腐层双层结构微体元分解图

工程中，3PE防腐层因其电绝缘、防水性好、耐腐蚀等优点已成为管道防腐涂层的首选。由于环氧树脂的物理声学参数与3PE防腐层相近，因此本实验平台采用钢板与环氧树脂板结合形成双层板状结构来模拟管道防腐层双层结构进行损伤分析，其中含裂纹缺陷的钢板-环氧树脂板模型在仿真计算中的参数如表1所示。

表1 钢板-环氧树脂板双层结构参数

利用COMSOL仿真软件构建含裂纹缺陷的钢板-环氧树脂板双层结构仿真模型，其中钢板的长×宽×高为0.4 m×0.3 m×0.006 m，环氧树脂板的长×宽×高为0.4 m×0.3 m×0.004 m。

利用COMSOL仿真软件加载幅值为0.1 mm、频率2.5 MHz的正弦交变力作为钢板-环氧树脂板结构的激励源，超声波激励信号如公式(26)所示：

(26)

通过COMSOL仿真依次均匀改变裂纹的长度，长度范围为4 cm到40 cm，间隔0.8 cm，对钢板-环氧树脂板双层结构进行动态仿真，通过超声导波进行缺陷检测获取损伤状态下的固有频率值，其动态仿真结构图如图7所示。

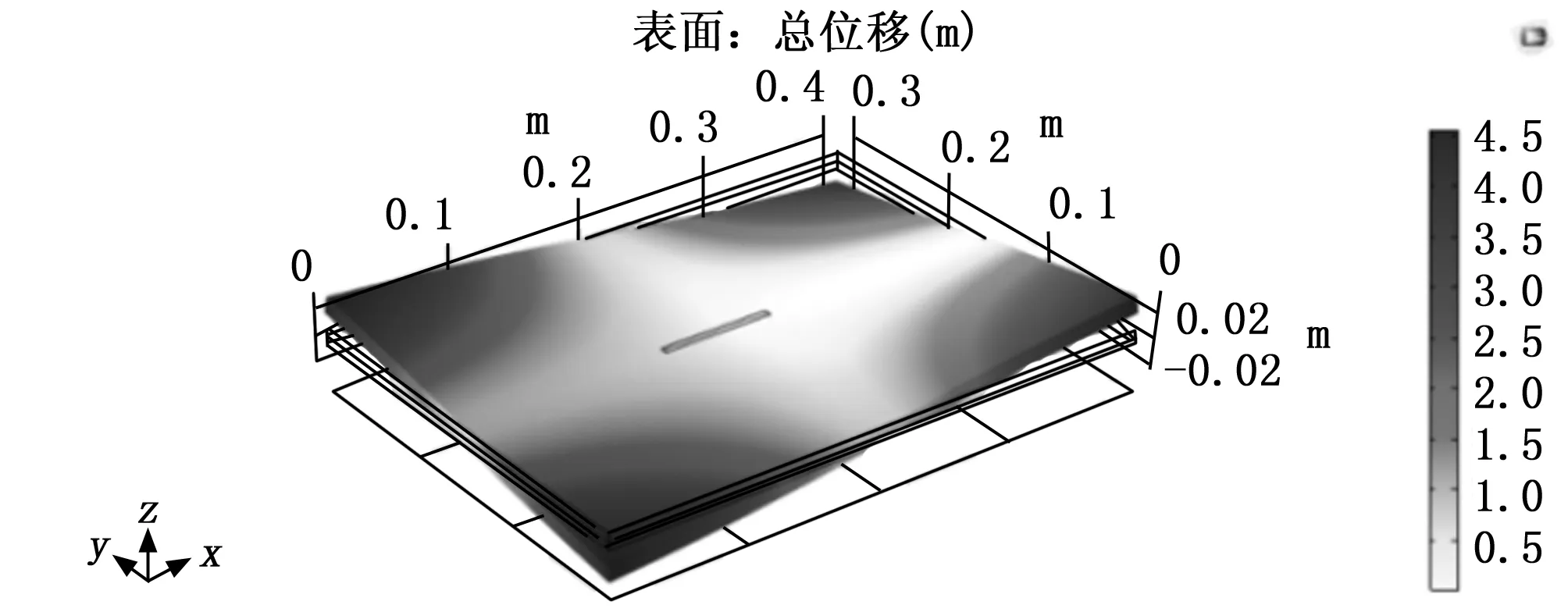
图7 含裂纹缺陷的钢板-环氧树脂板动态仿真结构图

由于六维裂纹损伤特征向量的可视化在二维平面中受限，因此以裂纹损伤数据集中的第三阶固有频率值为例进行分析，得到含不同损伤长度的裂纹的钢板-环氧树脂板双层结构的固有频率值的变化如图8所示。

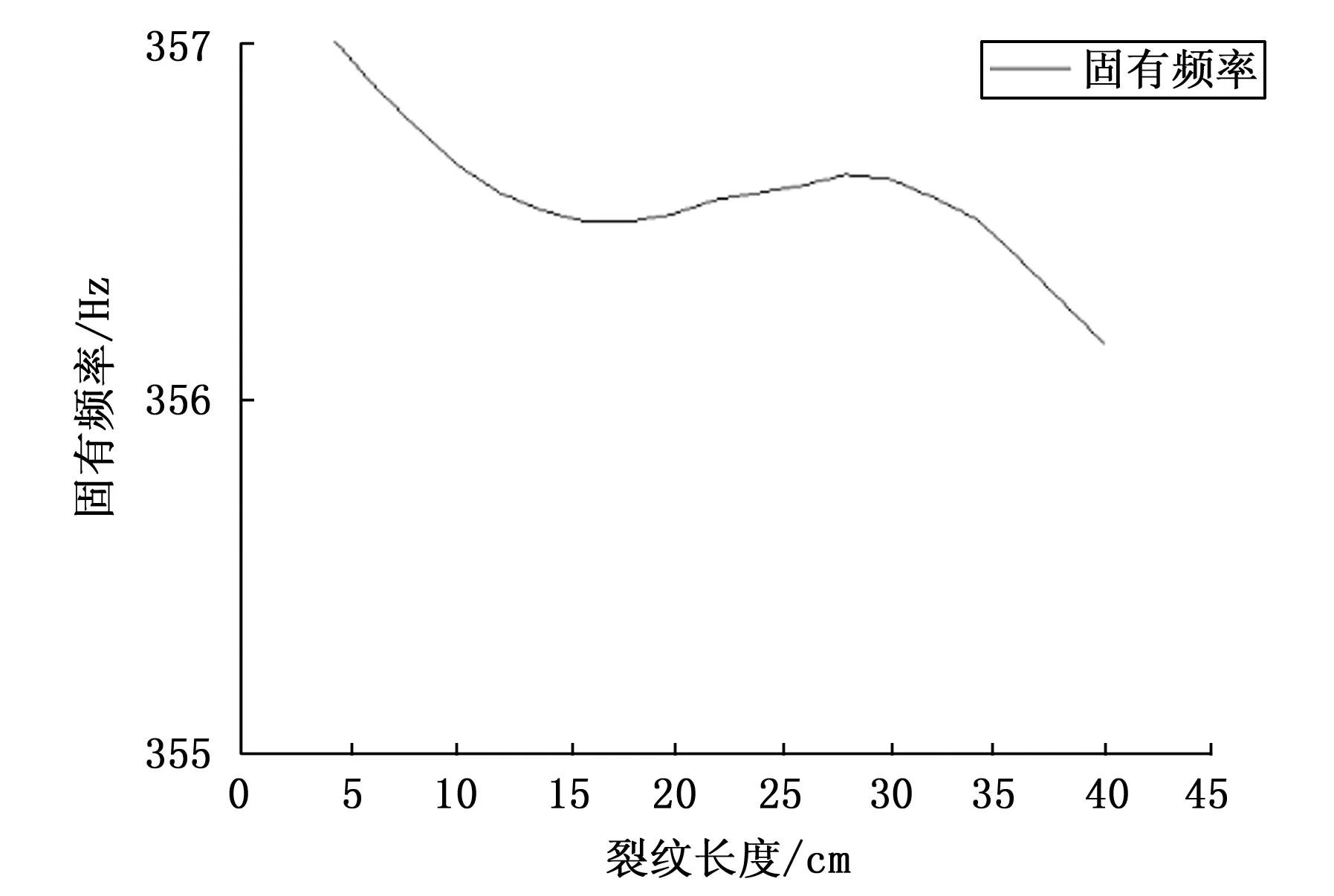
图8 不同裂纹长度的管道-防腐层结构固有频率值

由图8可知，在钢板-环氧树脂板双层结构中，结构的固有频率值随着裂纹长度的增大呈现出逐渐减少的趋势，表明结构的固有频率值与裂纹损伤长度之间存在相关性，为后续使用XGBoost回归算法实现管道防腐层裂纹损伤长度判定提供了理论基础。

4 含裂纹的管道防腐层现场实验

含有裂纹缺陷的管道-防腐层双层板状结构设计为为双层板上层为钢板，下层为环氧树脂板，钢板的长×宽×高为0.4 m×0.3 m×0.006 m，环氧树脂板的长×宽×高为0.4 m×0.3 m×0.004 m。在钢板上放置发送和接收两个探头，现场实验中选取频率为2.5 MHz，K=2的斜探头激发超声导波，其中斜探头的指标如表2所示。

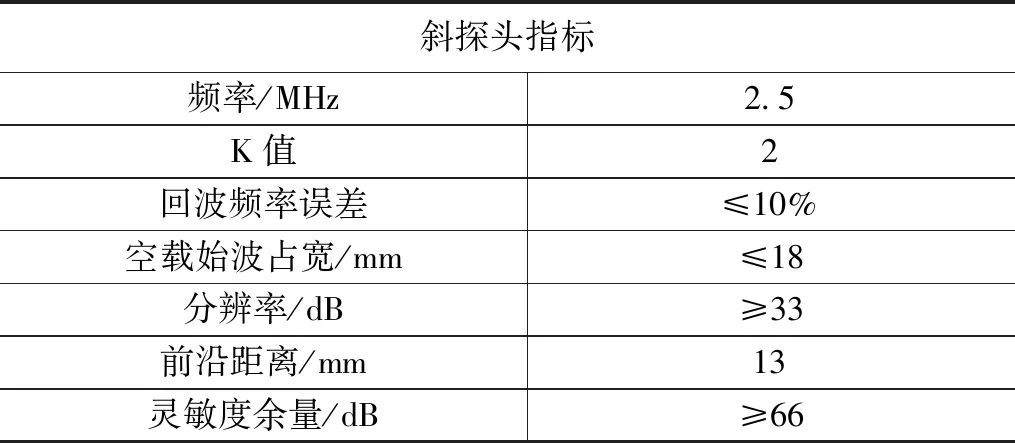
表2 超声导波斜探头指标

利用超声导波接收探头采集含裂纹缺陷的超声回波信号并使用示波器显示信号波形，分别对采集到的裂纹回波信号进行分析与处理，能够获取代表裂纹损伤特征的信息，其中不同损伤长度的裂纹具有不同的损伤特征。

实验中保持环氧树脂板中裂纹的宽度为4 mm，高度为3 mm，通过依次均匀改变环氧树脂板上裂纹的长度，分别采集裂纹长度从4 cm到40 cm(间隔0.8 cm)的超声回波信号，本文以裂纹长度为8 cm为例来分析，接收到的原始裂纹损伤信号对其进行EEMD时频分析，得到的结果图如图9所示。

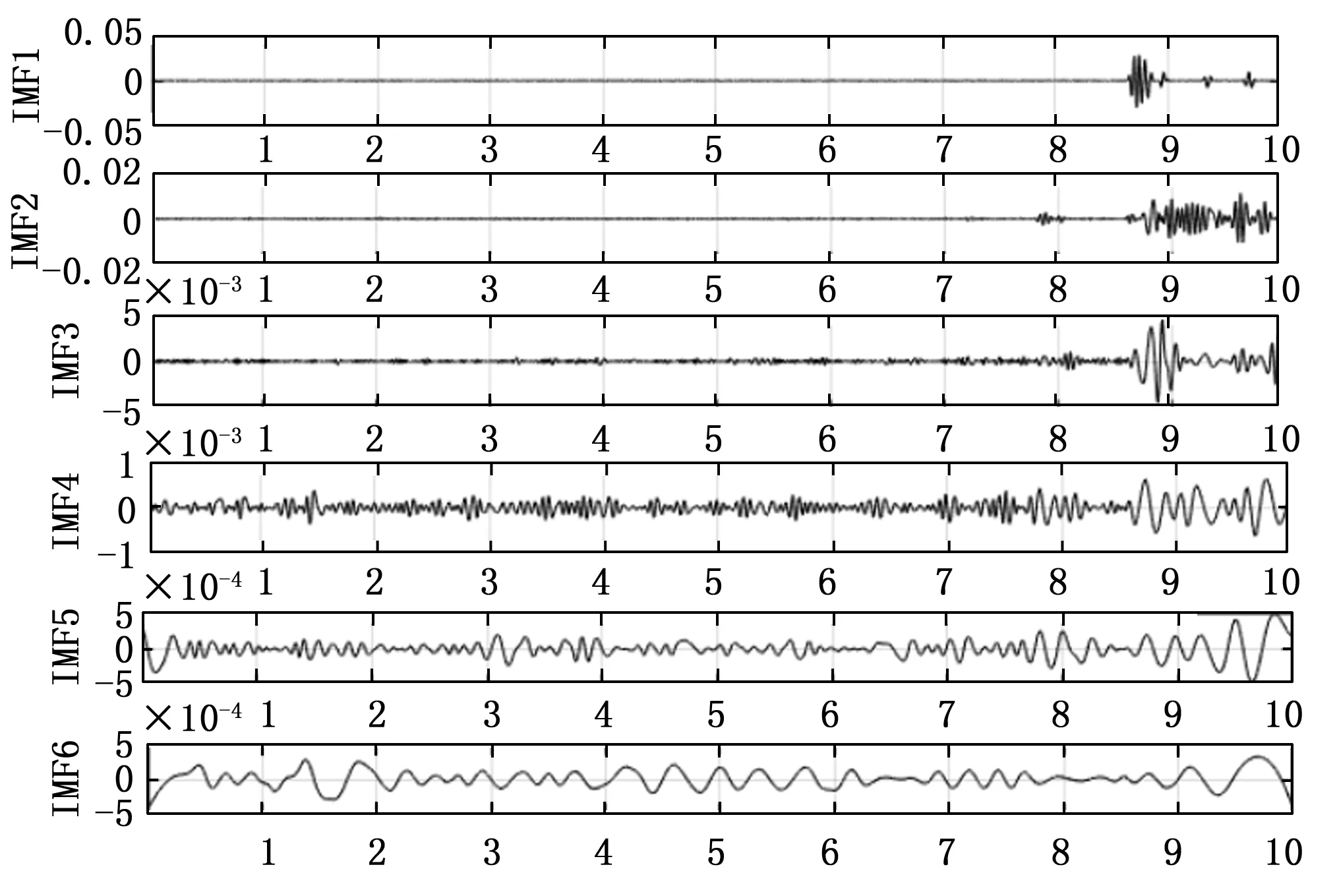
图9 原始裂纹损伤信号EEMD6阶分解

在管道-防腐层双层结构裂纹损伤识别中，首先分别对接收到的原始裂纹损伤信号进行时频分析，然后通过快速傅里叶变换分别对其进行频域的损伤特征提取，得到与损伤相对应的频域特征值。本文以裂纹长度为8 cm为例，对接收到的回波信号分别进行EEMD时频分析并将前6个IMF分量进行FFT变换，提取裂纹损伤信号频域特征量，如图10所示为管道防腐层双层结构裂纹损伤前后的信号频域特征量的对比。

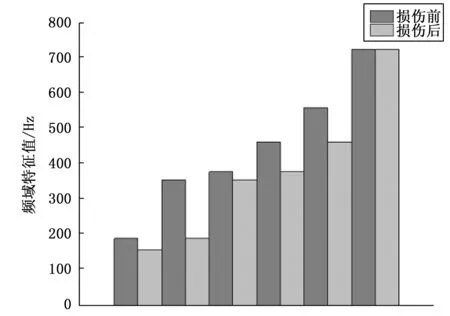
图10 管道防腐层结构裂纹损伤前后的频域特征值

由图10可知，当管道防腐层结构出现裂纹缺陷时，结构的频域特征值减小，验证了管道防腐层裂纹损伤动态仿真结论，为后续使用XGBoost算法对裂纹进行长度识别提供了支持。

5 裂纹损伤长度识别算法对比

针对管道防腐层裂纹损伤长度识别，采用裂纹损伤长度为4～40 cm(间隔0.8 cm)的46组样本，输入的频域特征值采用经过IForest异常检测、MF数据补全、KPCA降维优化后的损伤数据。

如图11和图12标准XGBoost 分类算法出现相对较多的测试误差，对管道防腐层进行损伤类型识别的精度相对较低，而应用IForest+MF+KPCA+XGBoost 分类算法的识别精度达到 90.9%，相比只采用标准XGBoost 分类算法的精度提高了 12.2%。其中，横坐标为样本数量，单位是(个)，纵坐标1，2，3分别表示裂纹，孔洞，剥离三种损伤类型。

图11 基于标准 XGBoost分类算法的结构损伤类型识别结果

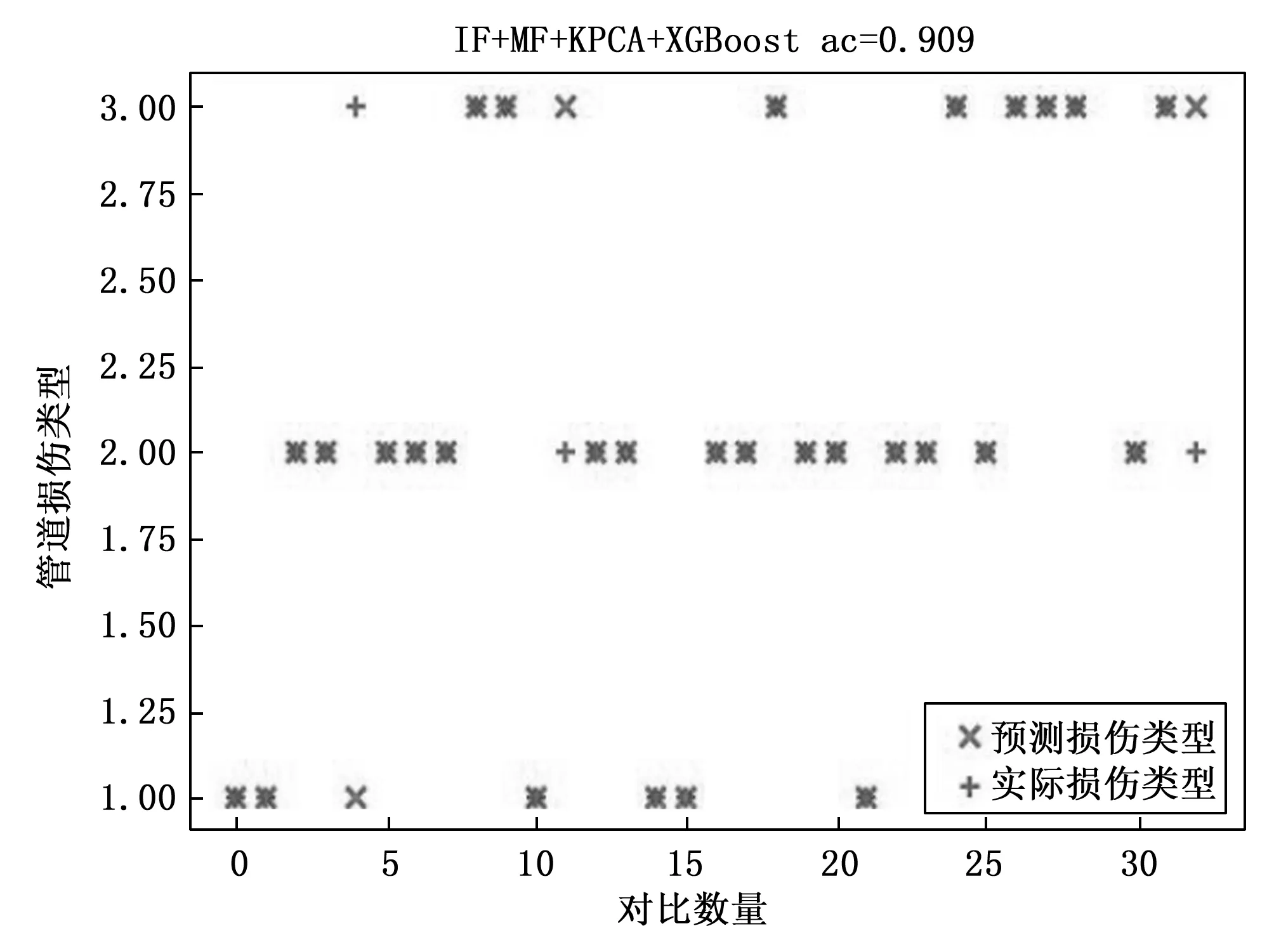
图12 基于IForest+MF+KPCA+XGBoost分类算法的结构损伤类型识别结果

本文分别采用XGBoost、GBDT、Random Forest三种算法对管道防腐层裂纹损伤长度进行判定，从上述构建的46组样本中选取36组样本作为训练样本，剩余的10组样本作为测试样本，选取均方误差和决定系数为性能度量。裂纹长度识别结果的均方误差(MSE)和决定系数分别如图13和图14所示。

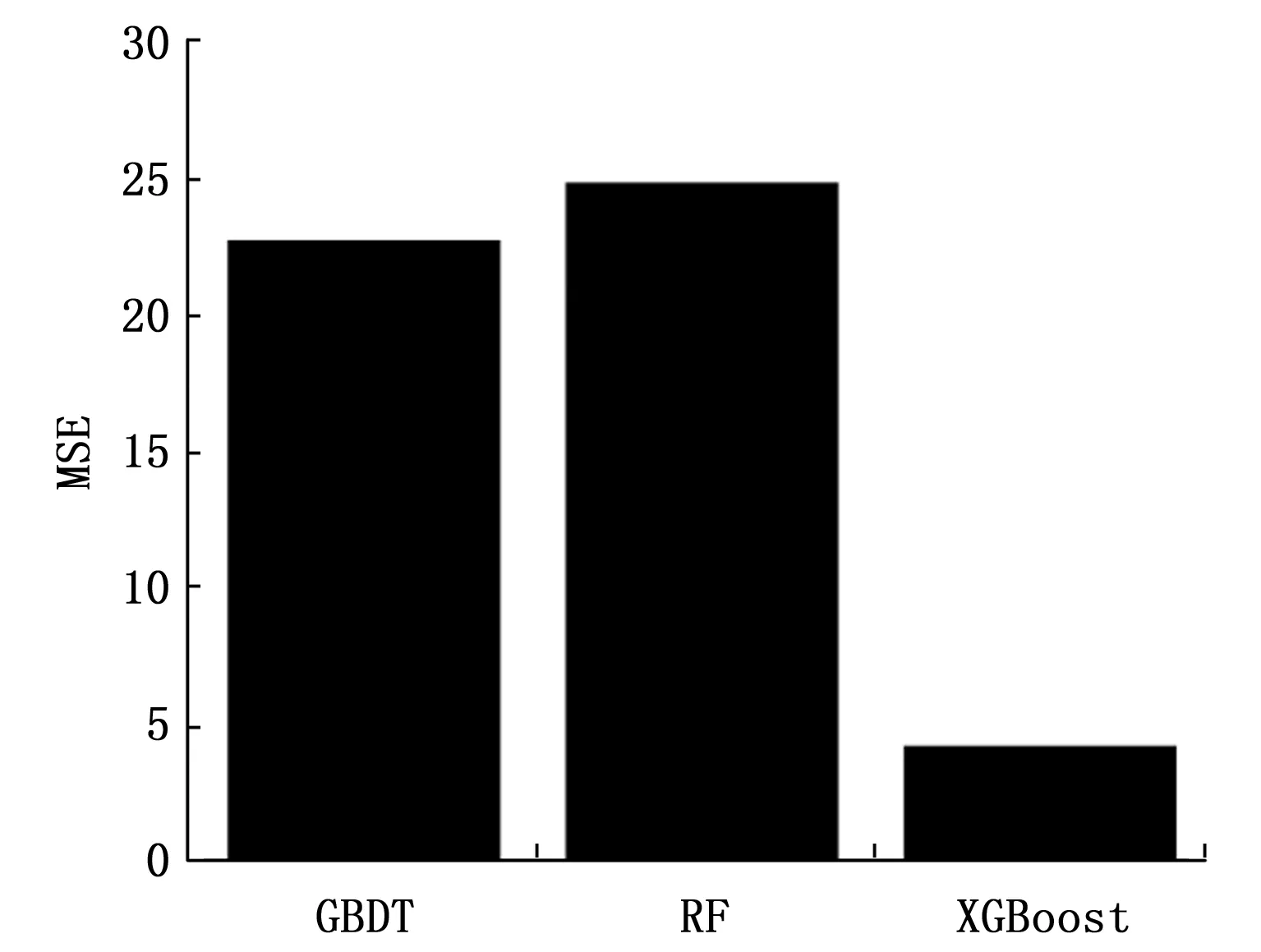
图13 MSE对比结果图

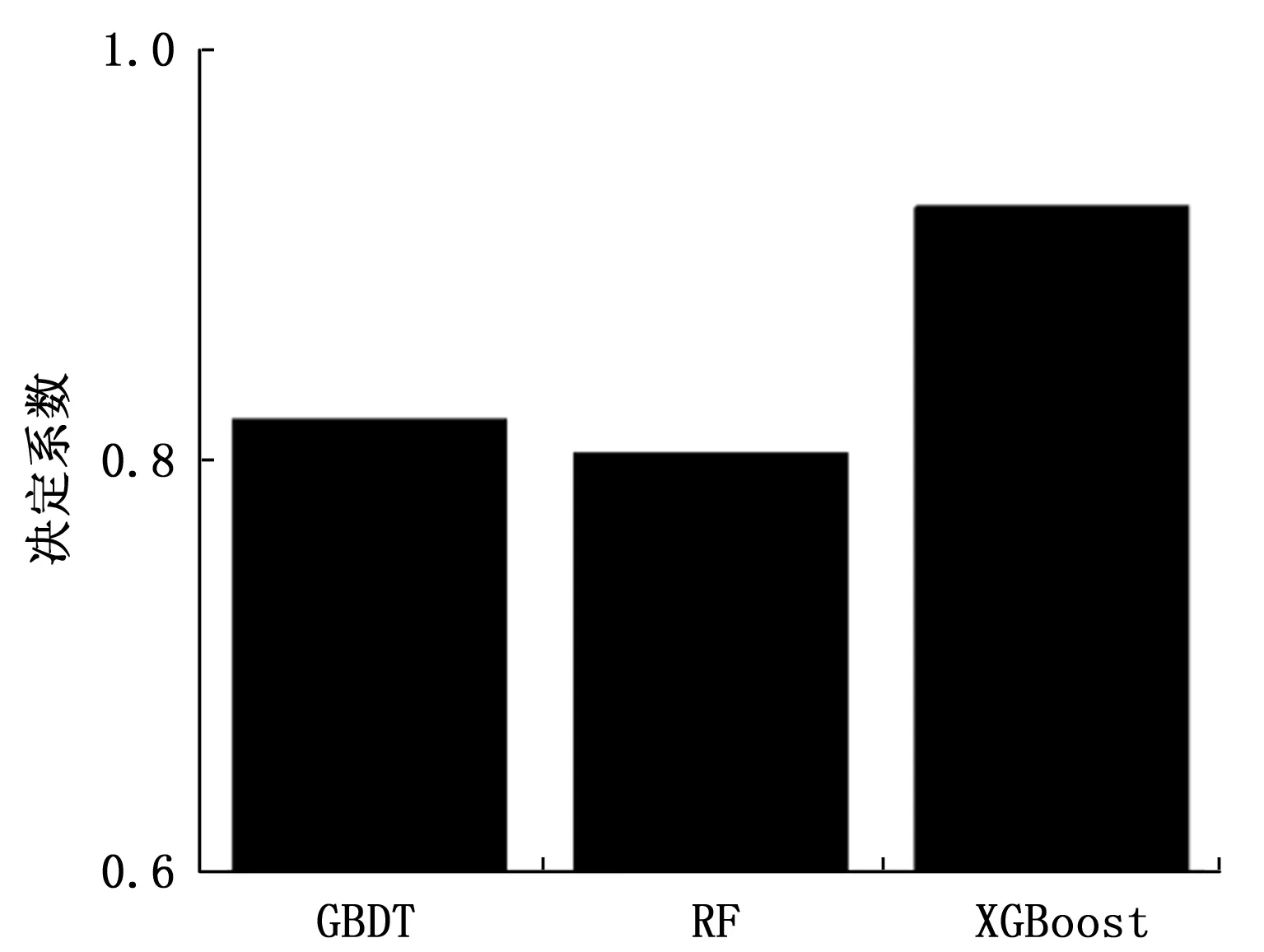
图14 决定系数对比结果图

由图13和图14可知，XGBoost回归算法的均方误差最小且决定系数最大，表明在管道防腐层裂纹长度识别中，XGBoost回归算法的效果最优，泛化能力最强。

XGBoost回归算法对裂纹损伤长度识别的结果图如图15所示，横坐标为对比数量，单位是(个)，在使用XGBoost回归算法对裂纹损伤长度进行判定时，设定max_depth为5，初始学习率为0.01，回归树的个数为500个。

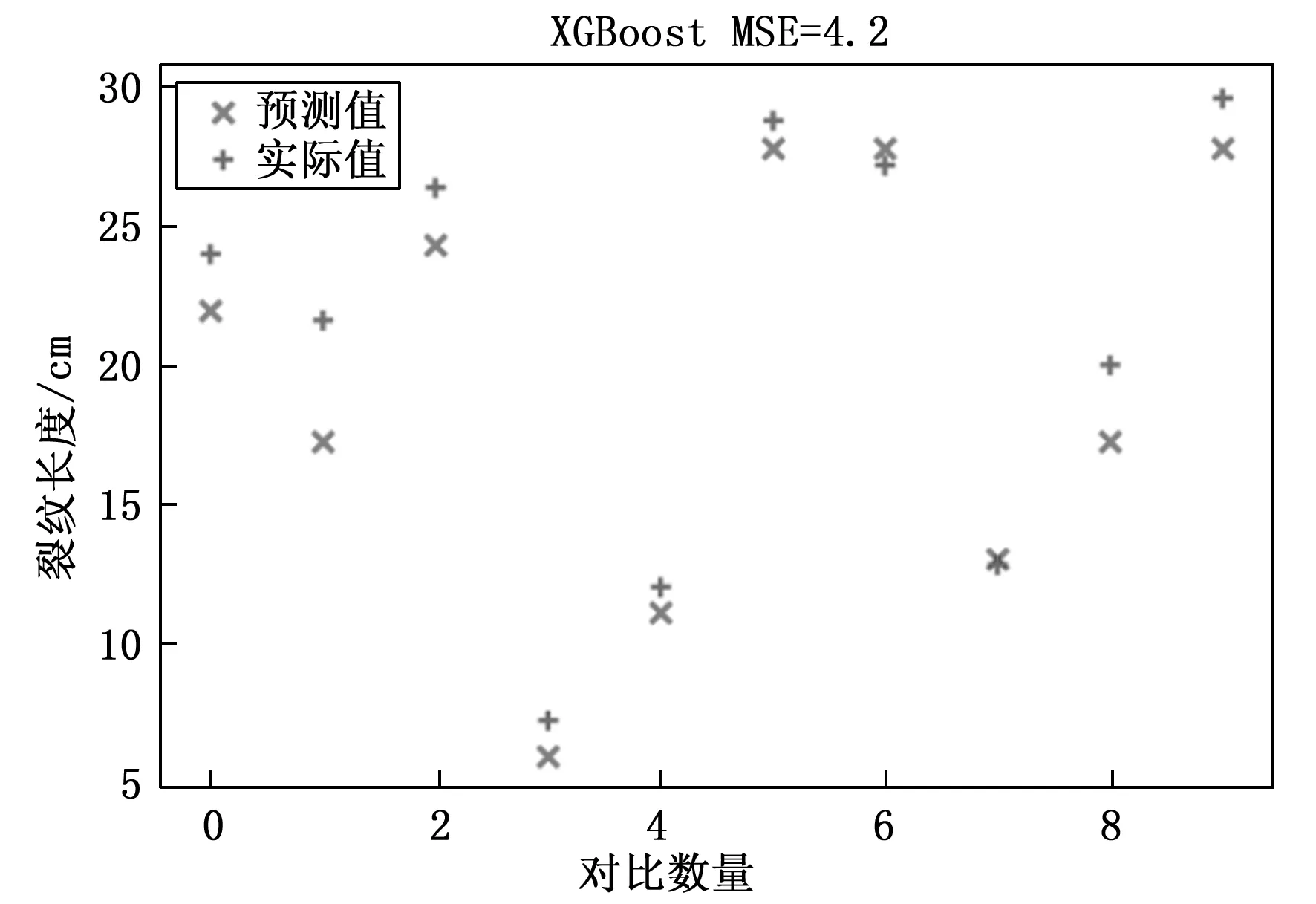
图15 裂纹损伤长度识别结果

XGBoost回归算法对管道防腐层的裂纹进行损伤长度识别输出的具体结果如表3所示。

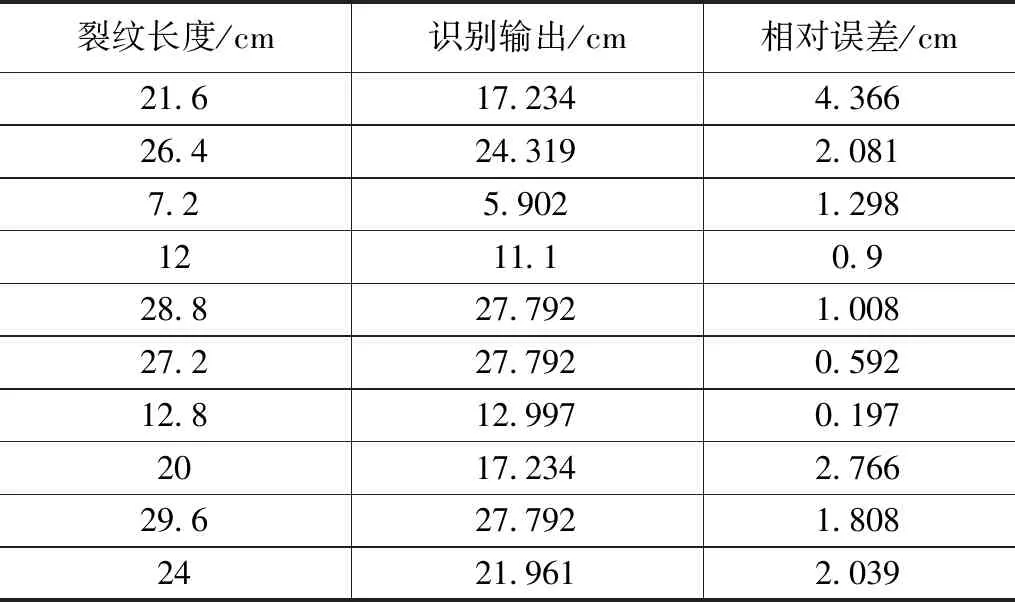
表3 裂纹损伤长度识别输出结果

根据表3可知，裂纹损伤长度的识别输出值与测试结果的最大相对误差在4.37厘米以内，平均误差为 1.706厘米表明使用XGBoost算法在管道防腐层裂纹长度识别方面表现良好。

6 结束语

本文引入集合经验模态分解、孤立森林、缺失森林、核主成分分析等方法，提出一种基于XGBoost的管道防腐层裂纹损伤长度识别方法。采用IForest+MF+KPCA+XGBoost 分类算法的识别精度达到 90.9%，相比只采用标准XGBoost 分类算法的精度提高了 12.2%，选取裂纹损伤信号的五阶固有频率作为管道防腐层裂纹损伤长度识别的特征向量，分别采用XGBoost、GBDT、RF三种回归算法对管道防腐层裂纹损伤长度进行判定。实验结果表明：应用XGBoost回归算法对裂纹损伤长度进行识别时，均方误差最小，决定系数最大，回归最大相对误差在4.37厘米以内，为管道防腐层结构裂纹智能化损伤检测提供了有效的识别方法。