城轨线路夜间全线单线双向行车模式下行车能力计算
2023-06-02杨在旭彭其渊周灿伟
杨在旭,彭其渊,赵 军,王 猛,周灿伟
(1. 西南交通大学 交通运输与物流学院,四川 成都 611756;2. 西南交通大学 综合交通运输智能化国家地方联合工程实验室,四川 成都 611756;3. 重庆市铁路(集团)有限公司,重庆 401121)
0 引 言
城市轨道交通以其安全、舒适、便捷及运量大的特点,逐渐发展成为我国居民出行所选择的主要公共交通方式。随着城市经济的发展以及居民生活水平的不断提升,国民的出行时间逐渐延长至夜间。由于部分通勤客流需求、大型交通枢纽间的交互客流需求以及某些繁华商区或大型活动对客流的影响等,城市轨道交通夜间客流需求不断增大。确定夜间行车模式并计算相应的夜间行车能力,是制定城市轨道交通线路具体夜间行车计划的前提和基础。在城市轨道交通夜间运营需求逐渐增大的背景下,结合我国城市轨道交通技术特点,合理协调夜间检修等工作,研究城市轨道交通夜间行车模式及夜间行车能力计算方法具有重要意义。
在夜间行车模式方面,现有研究人员大多将高速铁路夜间行车组织模式应用于城市轨道交通的研究上。彭其渊等[1]、朱绪斐[2]对高速铁路夜间行车的4种组织模式,包括等线、转线、一线维修一线行车以及基于客流规律的周期性行车进行了系统分析,提出了各夜间行车模式的技术要求及维修天窗协调要求;吴嘉等[3]探讨了城市轨道交通夜间延时运营的优缺点及发展意义,并对未来夜间运营模式提出了建议;陈虹兵[4]以广州地铁为例,分析了通宵运营的优缺点及运营组织模式;史丰收等[5]结合设施设备及客流需求,从线路设计、设备功能、客运服务等方面提出了未来新建线路通宵运营的相关需求。
在城市轨道交通线路行车能力计算方面,现有研究大多集中于考虑快慢车的能力计算。赵源等[6]分析了不同列车开行比例及越行次数对通过能力的影响,总结出不同方案下的通过能力计算公式;王晓潮等[7]给出了快慢车开行模式下基于易得参数的线路能力计算公式,分析了快慢车开行比例、越行站设置位置及数量对线路能力的影响;魏玉光等[8]将列车停站作业时间虚拟为一个闭塞分区来计算列车追踪间隔,给出了新的线路能力计算方法,并对快慢车开行及越行站的设置进行了研究。
目前,对城市轨道交通线路夜间行车能力计算方法的研究较少,全线单线双向行车模式(即全线2条正线中,一线双向行车,一线维修)的城市轨道交通夜间行车,与单线铁路线路日常行车存在某些相似性,因此,在进行轨道交通行车能力计算的研究时,可参考单线铁路线路行车能力的计算。
M. H. DINGLER等[9]采用仿真技术分析了不同类型列车开行对单线铁路能力造成的影响,包括客、货列车混跑,及单线重载铁路上不同类型货物列车混跑,得出了减少列车开行种类或均衡不同列车的优先级有利于增大单线铁路行车能力的研究结论;I. ATANASSOV等[10]对单线铁路不同扩能方案下的行车能力进行了仿真计算;C. T. DICK等[11]以总成本最小为目标,仿真分析了时刻表灵活性与线路扩建方案数之间的博弈关系,结果表明二者折中时可使总成本最小;M. C. SHIH等[12]建立了混合整数规划模型,对新建到发线的数量及位置进行优化,实现了单线铁路的扩能;A. JAMILI[13]从计算压缩运行图时所需的最小缓冲时间的角度,提出了新的单线铁路能力计算方法;严余松[14-15]提出了求解单线铁路线路采取成对非追踪平行运行图时最小运行图周期的整数规划模型,采取穷举的方式进行求解,并设计了遗传算法以改进求解方法;LI Feng等[16]提出了考虑两方向均衡性及延误的单线铁路能力计算模型;郑亚晶等[17]建立了混合整数非线性规划模型,既可求解行车能力,又可得到具体的运行图铺画方式,但该模型需预先计算好各区间在各铺画方式下的运行图周期以作为输入参数,前期计算工作较为繁杂;赵鹏等[18]基于文献[17]建立了单线铁路线路在成对追踪运行情况下通过能力的计算模型。
然而,城市轨道交通夜间行车与单线铁路行车在作业停站要求、停站时间、会车方案编制特点等方面不尽相同,因此,既有单线铁路线路行车能力的计算方法不能直接用于确定城市轨道交通线路夜间行车能力。
笔者提出了一个新的城市轨道交通线路夜间行车模式——全线单线双向行车,并对该模式下线路夜间行车能力的计算方法进行研究。首先,结合城市轨道交通在站作业相对单一、会车方案较简单的特点,提出了区间在不同运行线铺画方式下运行图周期的通用表达式,建立了全线单线双向行车模式下城市轨道交通线路夜间行车能力计算的混合整数线性规划模型,仅需输入线路基本参数即可直接用商业优化软件自动求得线路最优车站会车方案、最小限制区间运行图周期、以及夜间行车能力;然后,以一条实际线路验证了模型的可行性和有效性。
1 问题描述
1.1 全线单线双向行车模式
全线单线双向行车模式(图1)是指在具有2条及以上正线条件的城市轨道交通线路上,维修天窗开始时,全线进入单线双向行车模式,即1条正线进行日常检修,1条正线组织列车按成对非追踪方式双向运行,2条正线可交替进行双向行车,待维修天窗时间结束后全线恢复双线行车。

图1 全线单线双向行车模式示意Fig. 1 Illustration of the full line single-track bidirectional operation mode
全线单线双向行车模式的技术要求包括:整条线路具有丰富的车站配线条件,在必要站点合理设置配线以实现双向列车的交会;合理设置维修天窗开设形式和时长,2条正线的夜间检修可采取周期性交替检修,根据具体维保效率,可选择1 d为一个检修周期,每天2条正线分别检修2 h,或2 d为一个检修周期,每天检修1条正线,检修时间为4 h;在正常行车的正线上合理安排上下行列车在区间的运行线铺画方案、在车站的会车方案,缩短列车行车间隔,提高夜间行车能力。
全线单线双向行车模式的优点是:通过合理设定维修天窗和会车方案,理论上可实现城市轨道交通线路24 h连续运营,满足乘客夜间出行需求。其缺点是:需要会让车站配备良好的配线条件和完善的信联闭设备,增加了城市轨道交通线路建设/改造成本;当一条正线进行天窗维修时,另一条正常运行的正线为保证邻线维修施工的安全,可能需要适当限速或者避让,从而可能增加行车间隔,影响夜间行车能力。
可见,城市轨道交通线路采用夜间全线单线双向行车模式与单线铁路线路行车模式相似,但两者存在一定区别,主要表现在作业停站要求、停站时间长短、会车方案优化这3方面:
1)作业停站要求区别
城市轨道交通:在不考虑快慢车开行前提下,各个途径站均需停站。
单线铁路:仅在特定站点存在技术作业停站、客货运作业停站。
2)停站时间长短区别
城市轨道交通:旅客乘降停站时间短,在铺画运行图时,旅客乘降停站时间一般被纳入车站间隔时间里统一考虑。
单线铁路:技术作业停站时间较长,一般大于车站间隔时间,在铺画运行图时,技术作业停站时间及车站间隔时间需分别考虑。
3)会车方案优化区别
城市轨道交通:会车方案数有界。
单线铁路:会车方案数组合爆炸,无技术作业站均采用一停一通。
1.2 夜间行车能力计算问题
由于夜间采取2条线路交替检修的模式,而转线作业在一昼夜至多发生一次,此项作业对于总夜间最大行车能力的影响可通过作业时间的扣除进行计算。因此,城市轨道交通线路夜间最大行车能力计算问题的关键是夜间单线上双向行车的能力问题,即合理安排对向列车在会让站的会让作业。笔者所研究的问题建立在以下情境内:
1)线路及车站条件。城市轨道交通线路包含2条正线,日间运营时每条线路只供一个方向列车运行,夜间运营时2条正线交替使用,配线条件保证每条线路均可运行双向列车。线路包含多个车站,除两端折返站外,其余车站按线路条件分为会让站和非会让站。
2)其他设施设备。全线通信信号设备、列车控制系统,以及牵引供电模式、调度指挥模式等均满足双向行车条件。
3)相关能力。全线地下区间追踪能力、牵引供电能力、设备检修能力均满足夜间行车能力需求。
4)运营组织。线路夜间采用全线单线双向行车模式,列车采取单一交路站站停,同时由于一线维修一线行车,为保证邻线维修施工的安全,行车线路采取较日间运行更低的速度目标值。
图2为简易线路示意。线路包含车站A、车站B、车站C、车站D、车站E共5个车站及区间AB、区间BC、区间CD、区间DE共4个区间。

图2 简易线路示意Fig. 2 Illustration of a simple line
由各站配线情况可知,图2中C站为非会让站,其余车站均为会让站。由于夜间单线运营时,在非会让站同一时刻仅允许一列列车通过,列车在此仅进行简单的乘客乘降作业,故可将其近似视为正线的一部分。在计算夜间行车能力时,仅需考虑A、B、D、E站的会让方式,即可将区间BC及区间CD合并,分别将上、下行列车在C站的停站作业时间纳入新区间BD的上、下行区间运行时间一并考虑。因此,研究问题为合理安排列车在所有会让站的会让方式,并确定线路夜间最大行车能力。
2 模型构建
2.1 车站会让方式分析
由于城市轨道交通线路车站作业较为简单,仅为会让作业与基本乘降作业的协调。鉴于单线铁路线路列车在站会让方式共有8种[14-15],结合城市轨道交通的特征,笔者总结出城市轨道交通线路在各会让站的会让方式只有2种,但考虑到线路端点站的特殊情况,则可细分为4种,如图3。图中,根据实际情况设定会车间隔时间均大于最小停站时间。

图3 车站会让方式示意Fig. 3 Illustration of train meeting modes at stations
2.2 区间运行线铺画方式分析及规律总结
表1给出了相关符号含义。

表1 符号及其含义
将图3中相邻两会让站不同会让方式进行组合,最终可形成8种区间运行线铺画方式(包括端点站特殊情况),结果如图4。
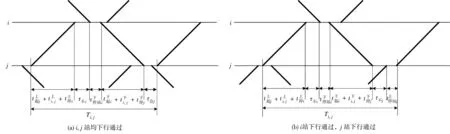

图4 区间运行线铺画方式示意Fig. 4 Schematic diagram of section operation line drawing mode
图4中,各区间在各运行线铺画方式下的运行图周期Ti,j按式(1)计算:
(1)
式(1)中,按从左到右的顺序罗列了各区间在各运行线铺画方式下Ti, j所包含的要素。可见,各区间在不同运行线铺画方式下,Ti, j的表达式有明显规律可循,且Ti, j仅与区间两端会让站所采用的会让方式有关。其中,上、下行列车的区间运行时间及基本的起停车附加时分为共同项,区别在于上、下行列车在区间两端点站因会让方式不同而产生的额外作业时间。
为便于规律总结,笔者引入0-1变量xi来表示上、下行列车在i站的会让方式。xi= 0表示在i站上行列车会让下行列车,如图4(a)、(b);xi= 1表示在i站下行列车会让上行列车,如图4(c)、(d)。如此,式(1)可简化为式(2)—式(6):
(2)
(3)
(4)
(5)
(6)
2.3 夜间行车能力计算
根据单线铁路线路通过能力计算原理[11-15],最大化城市轨道交通线路夜间行车能力等价于最小化限制区间的运行图周期。以最小化最大区间运行图周期为目标函数,可将全线单线双向运行模式下城市轨道交通线路夜间行车能力计算问题构建为0-1非线性规划计算模型(7):
(7)
非线性模型不利于求解,因此引入中间变量T,并增加约束条件,模型(7)可转化为线性规划计算模型(8):
(8)
随着城市轨道交通线路区间数的增加,混合整数线性规划计算模型(8)的规模呈多项式有界,应用于实际问题时,可采用商业优化软件如CPLEX、GUROBI、LINGO等直接有效求解。
在获得模型(8)最优解后,可利用式(9)计算城市轨道交通线路在全线单线双向行车模式下的夜间行车能力n全单:
(9)
式中:T运营为夜间总运营时间;T转线为双线交替运行时夜间列车转线作业时间,若线路采取2 d以上(含2 d)为一个检修周期,则T转线= 0。
3 案例分析
3.1 案例概况
为验证模型(8)的可行性,笔者选取某在建城市轨道交通线路进行分析。该线路为某区域综合交通体系的重要组成部分,连接机场及高铁站,服务于商务客流、机场客流、区域组团客流等,存在一定的夜间客流需求。为满足夜间行车,需先评估该线路在采用全线单线双向行车模式下的夜间行车能力。线路总体为直线型,共包含8个站点,其中A站为城市航站楼站,H站连接机场,E站连接高铁站。线路工可报告给出的配线设置如图5,其中D、F、G站不具备会让条件。
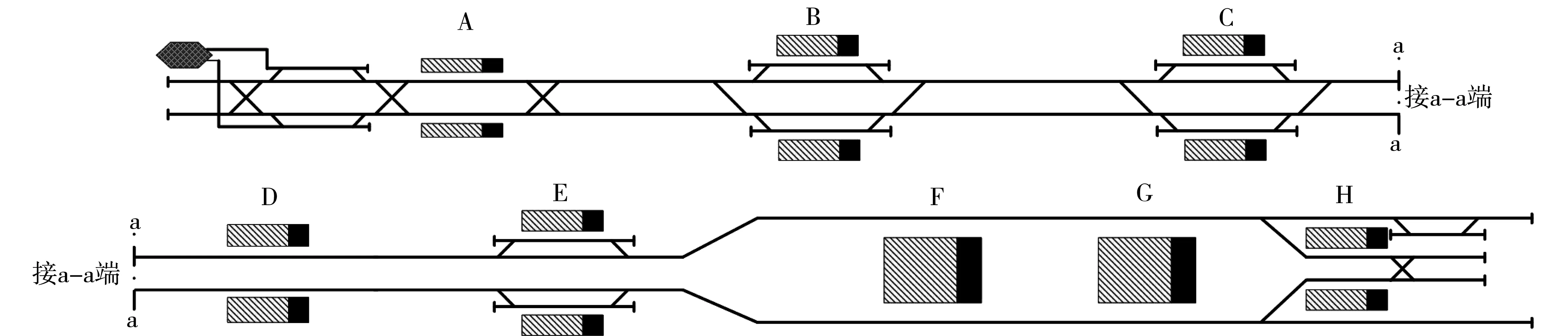
图5 测试线路配线设置示意Fig. 5 Schematic diagram of testing line siding tracks setting
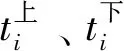
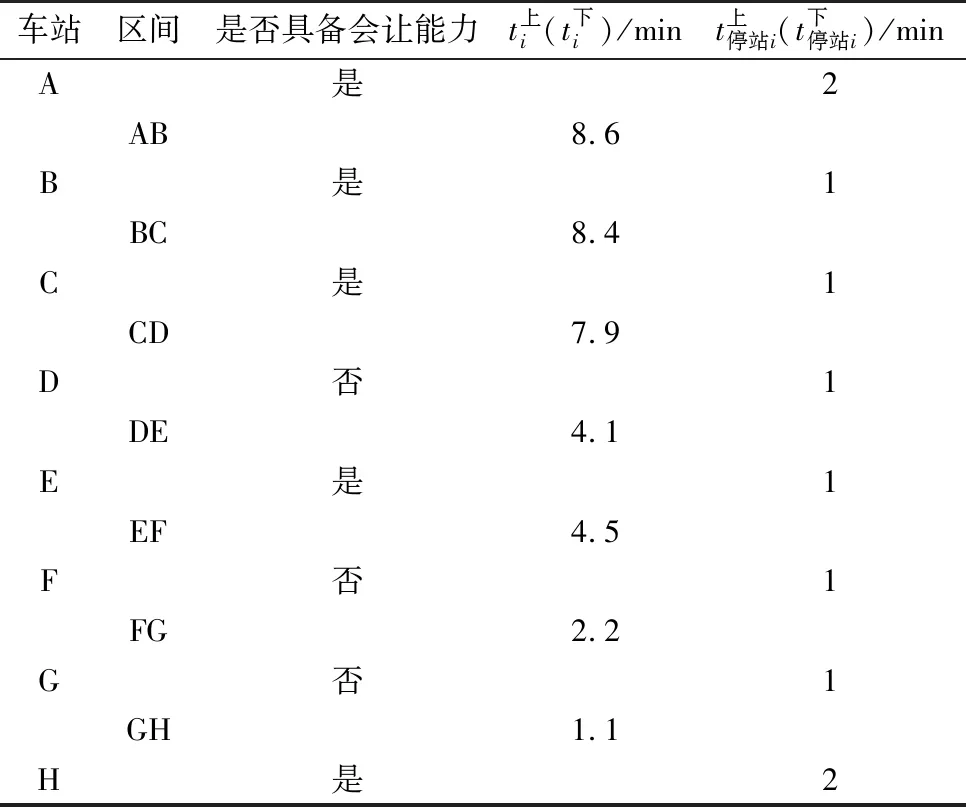
表2 测试线路车站及区间参数
3.2 计算结果
首先,根据各站的具体会让能力对区间进行处理,即将不具备会让能力的站点前后区间进行合并,合并后区间参数如表3。

表3 合并后区间参数
使用商业软件LINGO求解模型(8),确定测试线路夜间行车能力,耗时0.04 s获得模型(8)的最优解,计算结果见表4,所对应的运行图铺画方案见图6。
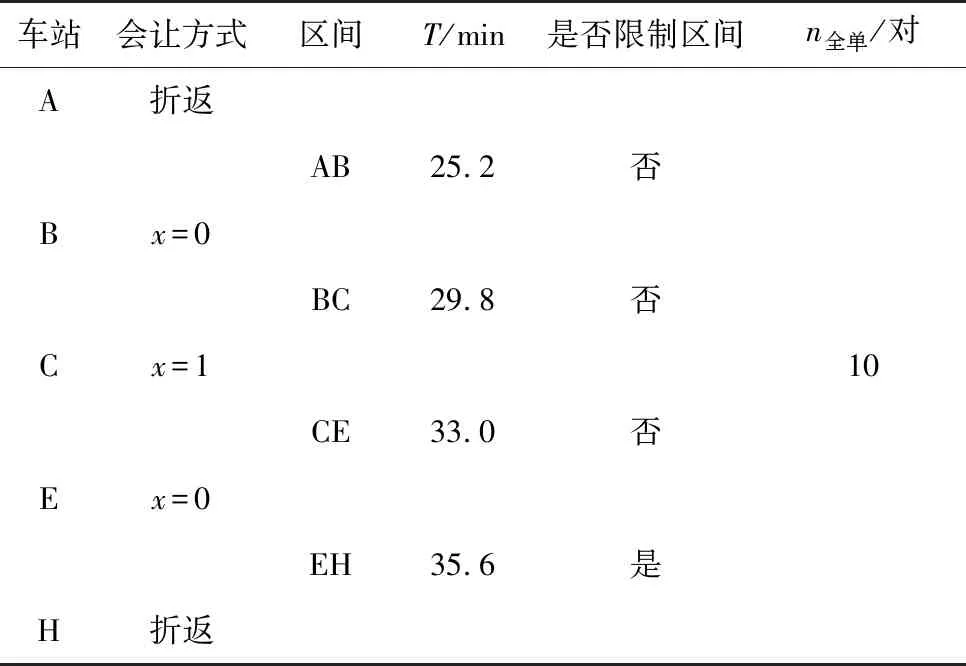
表4 计算结果
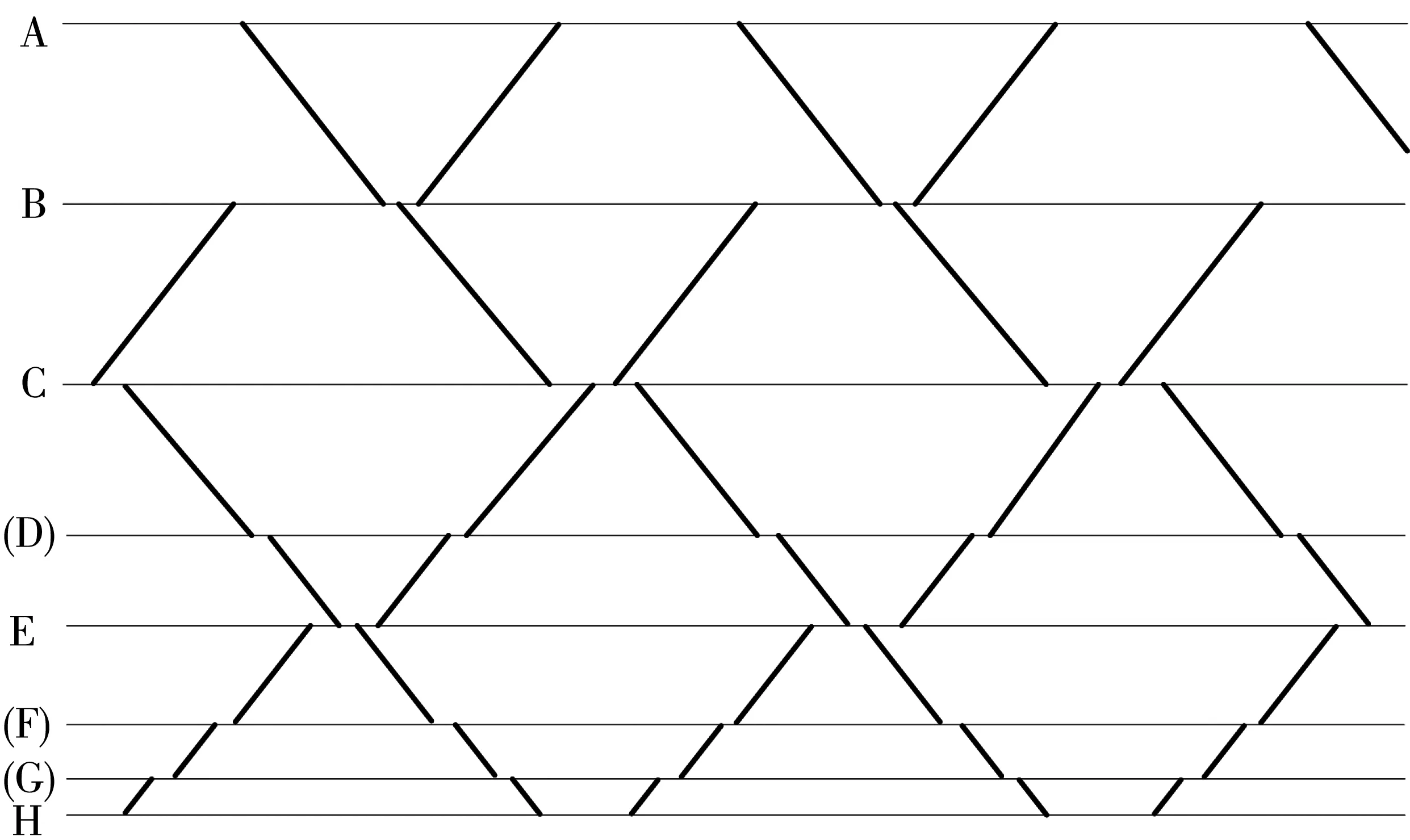
图6 运行图铺画方案Fig. 6 Drawing plan of working graph
由表4和图6可见,测试线路采取全线单线双向行车模式开行夜间列车的限制区间为EH,该区间运行图周期T= 35.6 min,根据式(9)计算得到该线路夜间6 h总行车能力为n全单= 10对。计算结果获得测试线路业主认可,并用于工可设计时夜间行车模式评估和夜间行车计划编制。
可见,只需输入线路基本参数,通过夜间行车能力规划计算模型(8)可快速求得线路的最优车站会车方案、最小限制区间运行图周期及夜间行车能力。实例分析结果验证了计算模型的可行性和有效性。
3.3 不同配线条件下夜间行车能力的对比
配线条件对城市轨道交通线路在全线单线双向行车模式下的夜间行车能力具有显著影响。为评估配线条件对夜间行车能力的影响,现通过在D、F、G站按任意组合增设配线,共构造7种新的配线方案。表5为各方案夜间行车能力计算结果。
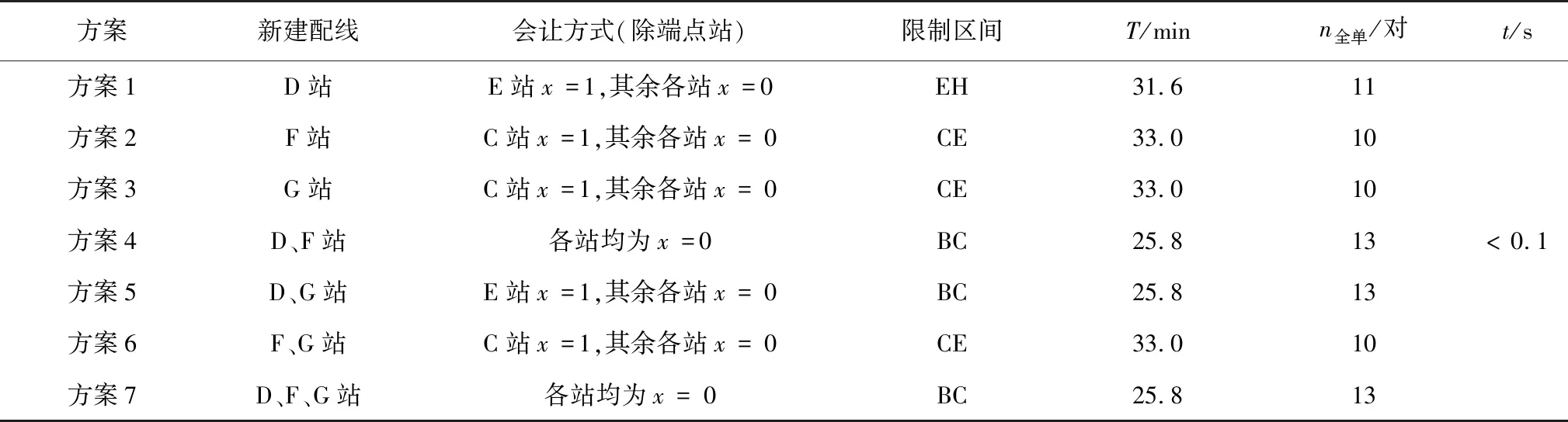
表5 不同配线条件下夜间行车能力对比结果
对比表5与图5的基准配线条件发现:新建配线方案2、方案3和方案6不能提高夜间行车能力,即在F、G站增设配线不利;新建配线方案1相比基准配线夜间6 h总行车能力可增加1对,即在D站增设配线有利;新建配线方案4、方案5和方案7可获得最大的夜间6 h总行车能力,达到13对,从经济学角度考虑,应在D、F站或者D、G站增设配线。
可见,在不具备会让能力的站点增设配线,使其变为会让站,即通过改变限制区间两端站点的会车方式、或者直接转换限制区间,能够在不同程度上增大夜间行车能力。具体新建配线站点的数量及位置需结合夜间客流需求规模、在站点增设配线的工程费用等因素进一步优化求得。
综上,笔者提出的夜间行车能力规划计算模型在7个配线方案下均可快速获得最优的夜间行车能力,适用于不同配线条件下的夜间能力计算、评估与分析。
4 结 语
研究了全线单线双向行车模式下,城市轨道交通夜间行车能力计算方法。提出了基于全线单线双向行车模式的,城市轨道交通线路夜间行车最小运行图周期的混合整数线性规划计算模型。实际案例分析表明,模型计算简洁,计算结果可靠,模型可用于不同配线条件线路夜间行车能力的计算。
