有心圆锥曲线中的一组调和点列

山东省邹平双语学校 (256200) 信统帅 姜坤崇

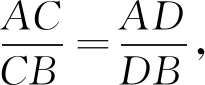
图1

AB

C

D

A

B

C

D

.

本文介绍有心圆锥曲线(椭圆或双曲线)中与调和点列有关的一个结论,以飨读者.

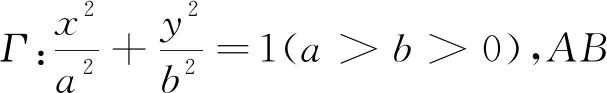
证明:设P(x0,y0),则切线l的方程为b2x0x+a2y0y-a2b2=0①.

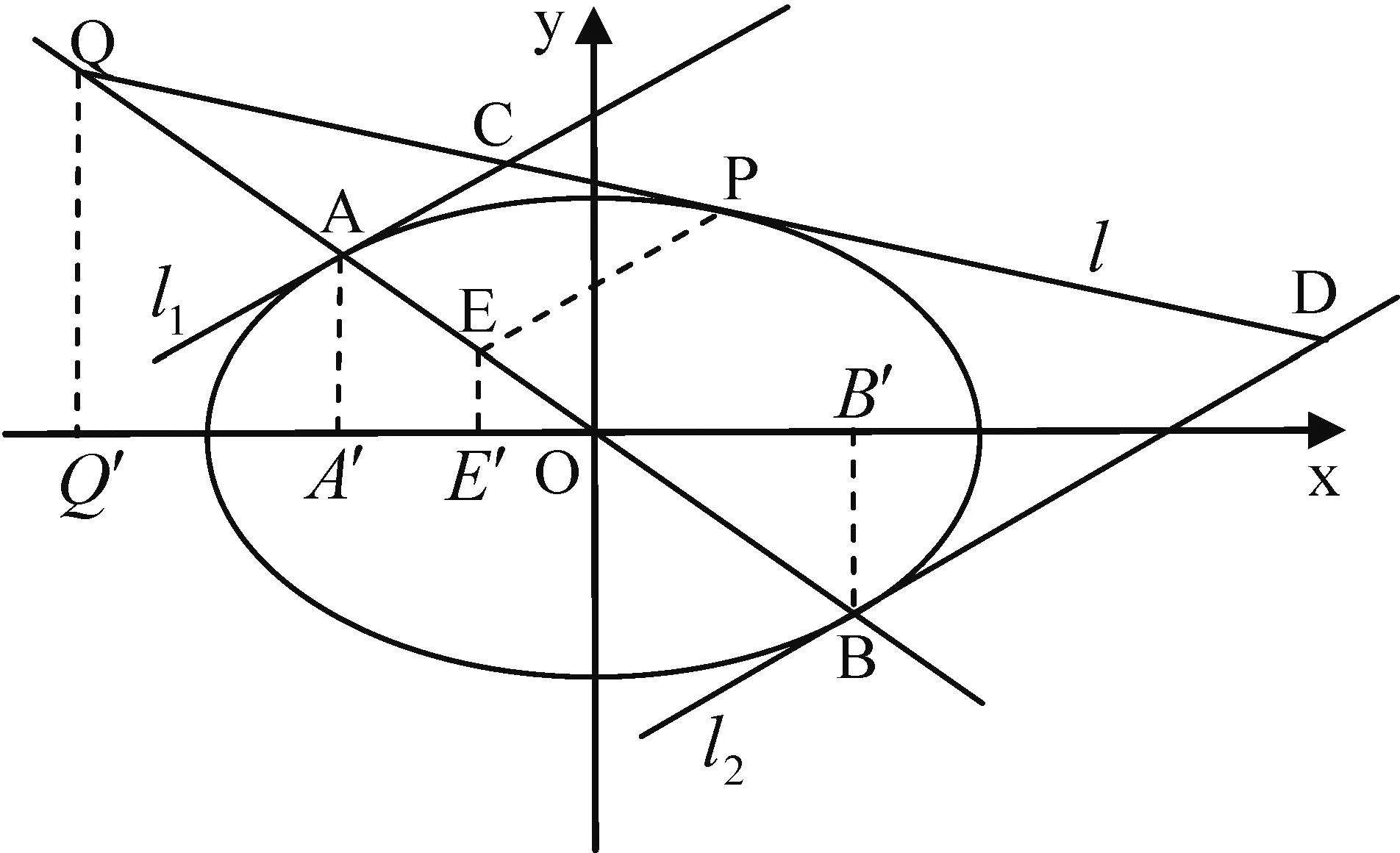
图2

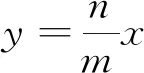
|E′A′|·|Q′B′|=|E′B′|·|Q′A′|⟺

⟺(b2mx0+a2ny0-a2b2)(b2mx0+a2ny0+a2b2)=(b2mx0+a2ny0+a2b2)(b2mx0+a2ny0-a2b2).

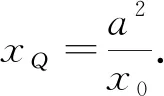
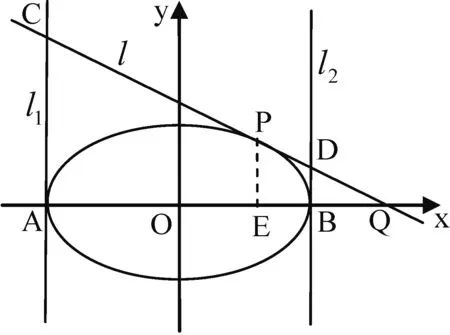
图3

当A、B为Γ短轴的两端点时,同理有C、D,P、Q是一组调和点列的结论成立.

综合(1)、(2),定理1得证.

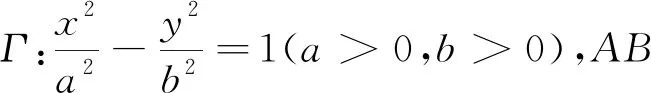
证明可仿定理1的证明进行,从略.