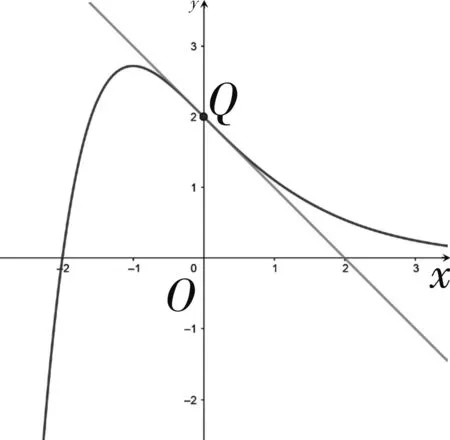
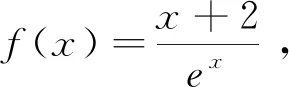基于直观想象探究一道切线问题
2023-06-01福建省安溪第一中学362400吴志湖
福建省安溪第一中学 (362400) 吴志湖
普通高中数学课程标准(2017版)指出,直观想象是指借助几何直观和空间想象感知事物的形状与变化,利用空间形式特别是图形,理解和解决数学问题的素养.直观想象是发现和提出问题、分析和解决问题的重要手段,是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础.笔者基于直观想象视角,探究一道曲线的切线问题.
一、试题呈现
题目(2022年武汉市高三年级九月调研考试第12题)已知函数f(x)=ex-1+lnx,则过点(a,b)恰能作曲线y=f(x)的两条切线的充分条件可以是( ).
A.b=2a-1>1B.b=2a-1<1
C.2a-1 本题主要考查导数的几何意义,函数与方程等知识,考查运算求解能力,推理论证能力,直观想象能力,考查化归与转化思想,数形结合思想,函数与方程思想,导向对直观想象,逻辑推理等核心素养的关注. 当a≤0时,令g′(x)=0,得x=1.当0 当0 当a>1时,易得g(x)在(0,1),(a,+∞)上递减,在(1,a)上递增.又x→0时,y→+∞;x→+∞时,y→-∞.当b=2a-1>1时,方程有两解,切线有两条,故选项A正确;而当2a-1 综上,本题选AD. 图1 点评:解法一通过定量计算,将切线条数转化为关于切点横坐标的方程解个数问题,最终解决问题.解法二通过定性分析,结合图像,直观解决问题.从解法二可知:过一点作曲线的切线,切线的条数问题与点在平面中所处的位置有关.结合函数的单调性和凹凸性,分析点与曲线、曲线拐点处的切线和曲线的渐进线的位置,我们便直观作出判断.基于直观想象,我们更容易窥得问题的本质,既可直观解决此类问题,还可洞悉作者的命题思路. 曲线的切线问题是高考的重要考查内容,以下继续解析两道高考试题,进一步感悟此类问题的直观解法. 例1 (2021年全国新高考Ⅰ卷第7题)若过点(a,b)可以作曲线y=ex的两条切线,则( ). A.eb C.0 解析:函数y=ex是凸函数且x轴是曲线y=ex的切线.由函数图像(见图2)可知,只有点(a,b)在渐近线上方,且在图像下方,才可作出两条切线.故选D. 图2 例2 (2022年全国新高考Ⅰ卷第15题)若曲线y=(x+a)ex有两条过坐标原点的切线,则a的取值范围是. 解析:由y′=(x+a+1)ex可知,函数y=(x+a)ex在(-∞,-a-1)上递减,在区间(-a-1,+∞)上递增.又x→-∞时,y→0,所以x轴是曲线y=(x+a)ex的渐近线.由y″=(x+a+2)ex可知,函数为(-∞,-a-2)的凹函数,区间(-a-2,+∞)上的凸函数.点(-a-2,-2e-a-2)为曲线的拐点,曲线在拐点处的切线方程为y+2e-a-2=-e-a-2(x+a+2),可求得此切线与x轴交于点A(-a-4,0). 又曲线y=(x+a)ex与x轴交于B(-a,0).做出简图(见图3),结合图3可知:只有坐标原点O在A点左侧,或者在B点右侧,才可做出两条切线. 图3 故-a-4>0或者-a<0,从而答案为a<-4或a>0.. 基于直观想象,我们可掌握此类试题的命题手法,进行试题命制.以下命制两道试题,供读者赏析. 试题1 若过点(1,0)可以作曲线y=ln(x+a)的两条切线,则实数a的取值范围是. 解析:曲线y=ln(x+a)有渐近线x=-a,且与x轴交于点A(1-a,0).结合图像(见图4)可知,点(1,0)应位于A与渐近线之间,故有-a<1<1-a,解得-1 图4 A.b=2-a>2B.b=2-a<2 C.2-a 图5二、解法探究
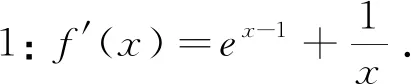

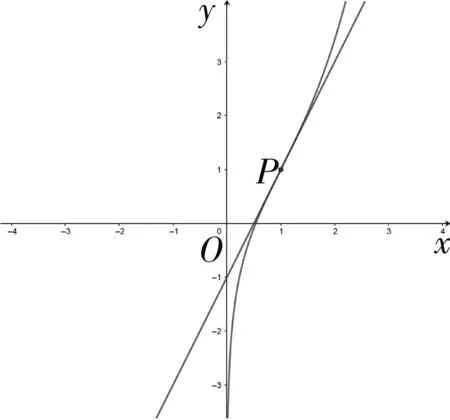
三、理解应用
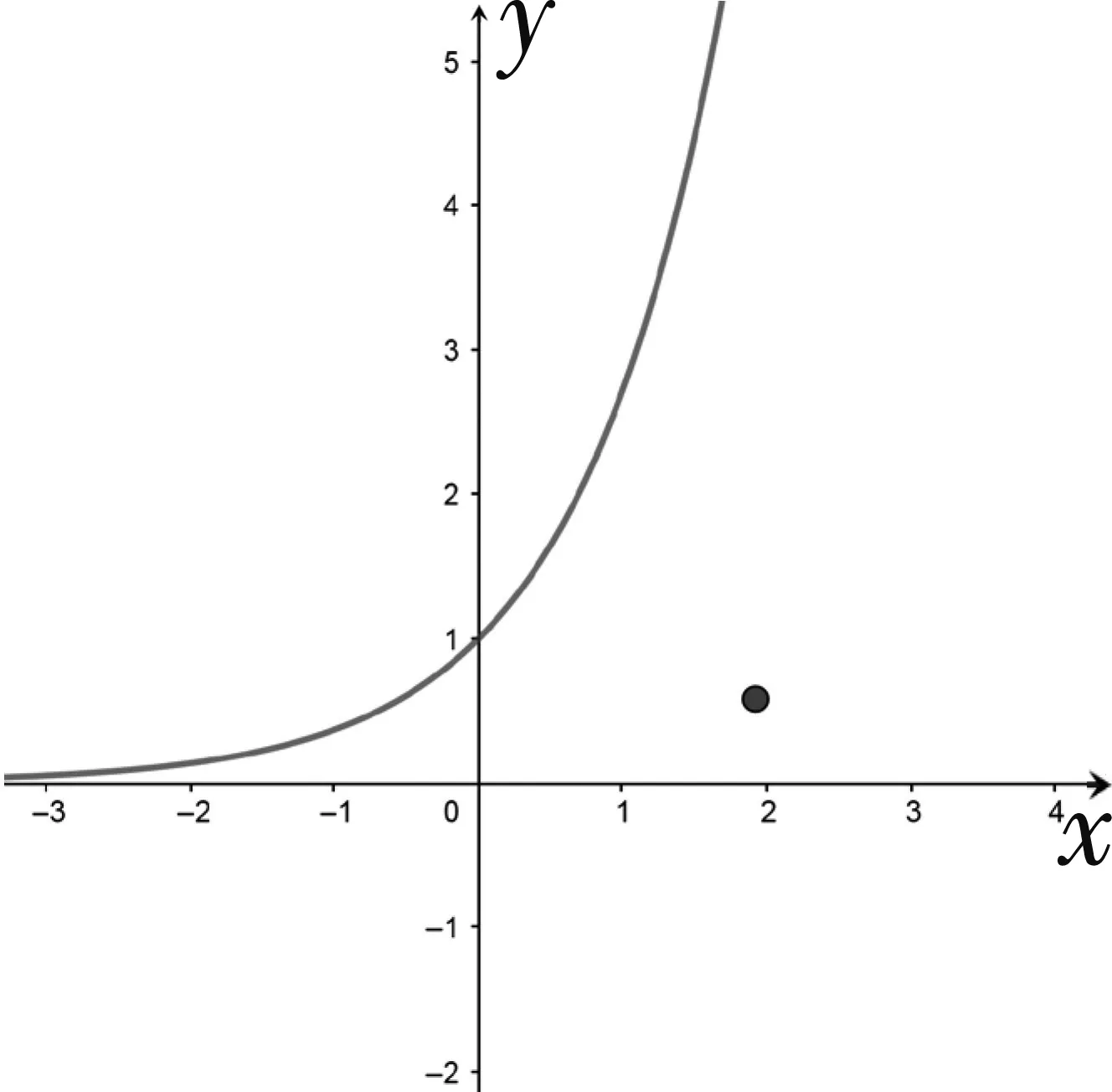

四、试题命制