中国PM2.5空间分布特征及影响因素
2023-06-01牛曦辰
牛曦辰
(长安大学理学院,陕西 西安 710064)
随着城市的发展,大气污染问题日趋严重,尤其是以颗粒物(PM2.5)为特征污染物的区域性大气问题更加突出,目前严重影响到人们的生活环境、身体健康,对城市的可持续发展造成了影响[1]。目前,如何缓解城市空气污染问题,实现城市的可持续发展,是政府和公民共同关注的重点之一。
随着遥感技术的发展,许多研究者从城市、区域、国家或全球的尺度来研究城市PM2.5的时空分布特征、影响因素或影响特征。从全球来看,中国、印度和东南亚是目前PM2.5污染最为严重的国家和地区[2-4];从国家来看,PM2.5污染严重的地方多集中于东部平原地区,尤其是京津冀城市群,四川省东部以及塔克拉玛干沙漠地区[5-7];从城市来看,郊区或农村的PM2.5质量浓度大多低于城区。大多学者从社会、经济、空间结构、环境等方面来了解城市PM2.5污染的成因。从社会经济角度看,PM2.5质量浓度的增加与城市人口及GDP 的增长呈线性关系[8],城市的第二产业占比也会显著增加PM2.5质量浓度[9-10];从空间结构看,城市规模、聚集程度、城市空间均会对PM2.5质量浓度产生影响[11];从环境角度看,绿地面积[12]、降水量、风速[13]等均会影响PM2.5质量浓度。然而,PM2.5质量浓度的变化往往不是由单一的社会因素或生态因素引起的,综合考虑不同地理条件下社会和生态的共同特征,方能发现影响城市空气污染物的因素。并且,PM2.5是城市的主要污染物,如何理解PM2.5在城市化的背景下的形成特征,针对污染物进行调控,是目前有待解决的问题。本文利用2020 年中国1 762 个县(区)级监测站点的PM2.5日均质量浓度数据,分析了PM2.5空间分布特征,进一步从社会生态角度探究了其时空分布的影响因素和特征,可为了解中国的大气污染状况、大气污染防治以及城市规划与布局提供数据支撑和理论依据。
1 研究区域及方法
在全国尺度和区域尺度上,PM2.5监测数据来源于中国环境检测总站:在本文的研究时段(2020 年),全国各城市范围内共选出1 762 个县(区)级监测站点,监测站分布如图1 所示。

图1 监测站点图
社会经济数据来自统计年鉴,气温、降水量数据来源于中国气象数据网。PM2.5质量浓度数据均按照《环境空气质量标准》中的规定进行质量控制,剔除无数据或异常值。分别采用ArcGIS、SPSS、R 等对原始数据进行整理分析、图形绘制、相关性分析。由于本文中的PM2.5是站点数据,在本研究中,在ArcGIS中将PM2.5年均值空间分布栅格数据进行市级划分,使用克里金插值法计算每个城市的PM2.5质量浓度,如图2 所示。
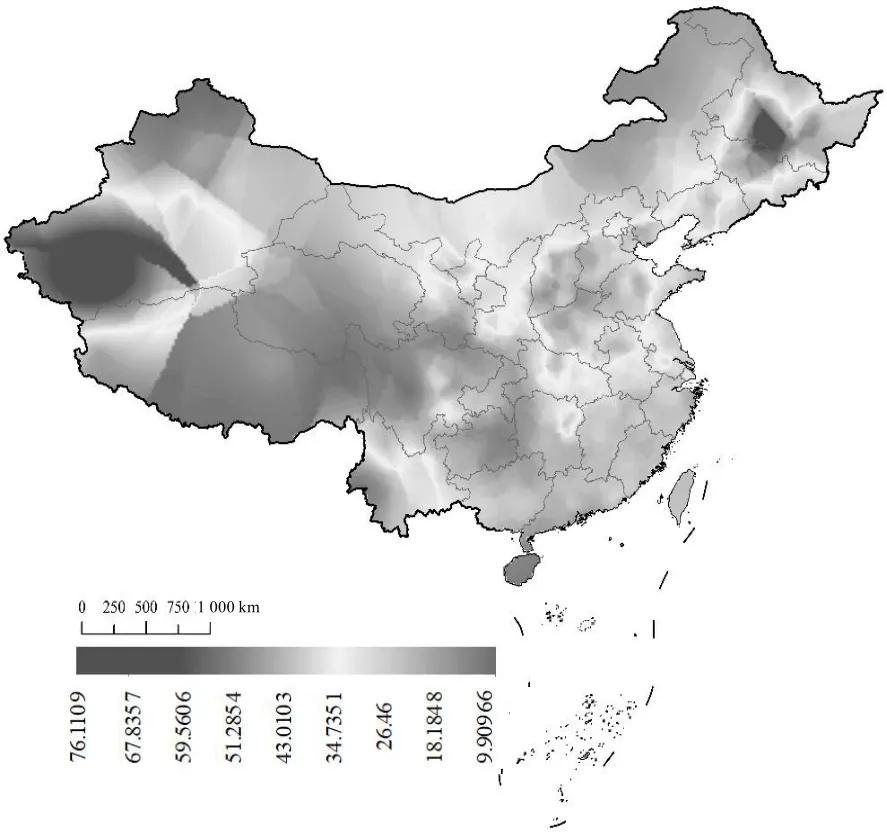
图2 PM2.5质量浓度图
2 中国PM2.5空间分布特征
地理学第一定律指出,任何事物之间都是相关的,离得较近的事物比离得远的事物相关性要更高。通过Moran'sI指数计算了相邻城市各典型污染物质量浓度在空间上的自相关特征,基于此指标探究各典型污染物污染是否存在显著的空间聚集性特征,即相邻城市的污染之间是否存在显著影响。
Moran'sI指数为:
检验统计量Z值为:
本文进一步用冷热点分析(Getis-OrdGi*)识别污染及其变化的高风险区域和低风险区域。该工具使用Z得分度量统计上的显著性。表达式如下:
根据冷热点分析,将变量空间分布聚集的程度通过冷点和热点体现。污染物PM2.5热点(高/高聚集)区域主要在河南、河北、山东、山西、吉林、黑龙江6个省份的交界处。污染物PM2.5冷点(低/低聚集)区域主要分布在广东省及沿海城市、新疆的边界地段。深层探究影响原因,首先是由于空气的流通性导致相邻省份受到了影响,其次由于气候、地理条件、经济条件等原因,导致污染程度不相同。综上可知,空气污染物的分布与地理位置有关。
冷热点如图3 所示。

图3 冷热点图
3 中国PM2.5影响因素研究
根据文献[8]—文献[13],可知影响PM2.5质量浓度的因素为社会、经济、空间结构、环境等。因此,本文从社会经济、空间结构、环境来考虑影响PM2.5的因素,共20 个可能因素,如图4 所示。

图4 影响因素分析图
4 主成分分析及空间自回归模型
4.1 主成分分析
4.1.1 主成分分析的适用性检验
首先对数据进行KMO 检验和Bartlett's 球体检验,结果如表1 所示。由表1 知KMO 检验值为0.754,满足主成分分析的条件。Bartlett's 球形检验结果显示各变量间具有相关性,可进行主成分分析。

表1 KMO 和Bartlett's 球形检验结果
4.1.2 主成分的提取
运用SPSS 对所选取的226 个城市的影响PM2.5质量浓度的指标进行主成分分析,得到各个成分的特征值及累加贡献率。解释的总方差如表2 所示,前7 个主成分的特征值大于1,累积贡献率为65.254。说明前7 个主成分能充分代表原数据,对总体起到概括作用,因子分析效果比较理想,因此本文提取前7 个主成分进行研究。
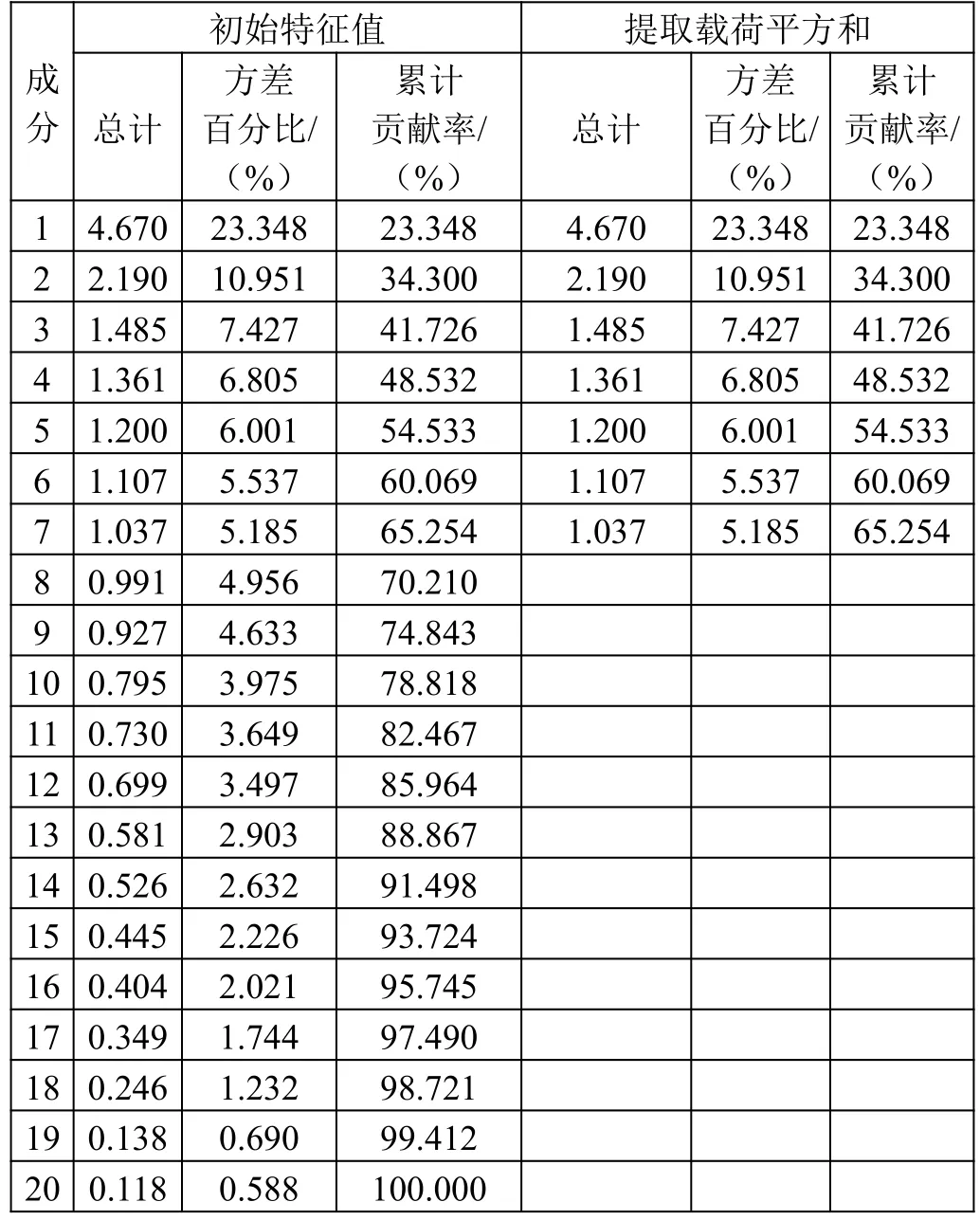
表2 解释的总方差
成分得分系数矩阵如表3 所示。

表3 成分得分系数矩阵
根据系数得分矩阵表,分别用F1、F2、F3、F4、F5、F6、F7表示7 个主成分,根据表中的数据可以得到各个主成分的表达式,如第一个主成分的表达式为:F1=-0.147x1-0.113x2+0.047x3+0.115x4+0.293x5-0.071x6+0.021x7-0.013x8+0.089x9-0.153x10+0.161x11+0.076x12-0.021x13+0.115x14-0.111x15+0.285x16+0.148x18-0.081x19+0.119x20,同理可以得到F2、F3、F4、F5、F6、F7主成分的表达式。
4.2 空间自回归模型
4.2.1 模型的构建
空间数据往往存在空间依赖性,若此时仍然采用传统的回归模型,通常会忽略这种依赖性而使回归结果产生偏差。PM2.5质量浓度具有显著的空间自相关性,本文考虑空间依赖性对PM2.5质量浓度的影响。
空间滞后模型通过引入空间滞后变量表示空间单元的因变量的观测值受到其相邻空间单元的观测值的影响,空间滞后模型表明个体的值会受到其周围地区的直接影响,基本形式如下:
式(4)中:ρ为空间回归相关系数;w为标准化的空间权重矩阵;y为因变量;x为自变量;β为待估系数;b为截距。
空间误差模型通过引入空间误差变量表示存在于误差中的空间依赖作用,空间依赖作用体现于误差项之中,基本形式如下:
式(5)(6)中:y为因变量;x为自变量;β为待估系数;ε为随机误差项;b为截距;λ为空间误差系数;w为标准化的空间权重矩阵。
空间杜宾模型是SLM 模型和SEM 模型的组合扩展形式,基本形式如下:
式(7)中:y为因变量;ρ为空间回归相关系数;w为标准化的空间权重矩阵;b为截距;x为自变量;β为待估系数,表示自变量对因变量的影响程度;θ为待估系数。
空间杜宾误差模型的基本形式如下:
式(8)(9)中:y为因变量;b为截距;x为自变量;β为待估系数,表示自变量对因变量的影响程度;w为标准化的空间权重矩阵;θ为待估系数。
嵌套的空间模型是具有所有类型的交互效应的完整模型,形式如下:
式(10)(11)中:y为因变量;ρ为空间回归相关系数;w为标准化的空间权重矩阵;b为截距;x为自变量;β为待估系数,表示自变量对因变量的影响程度;θ为待估系数。
模型关系如图5 所示。

图5 模型关系图
4.2.2 模型判别
回归模型结果如表4 所示。

表4 回归模型结果
为比较各个模型在PM2.5质量浓度影响因子分析中的结果,本文建立了OLS 模型,结果如表4 所示;此外本文考虑了由于不同地区的PM2.5质量浓度之间存在空间相关性,需要考虑建立空间回归模型,如SLM模型、SEM 模型、SDM 模型、SDEM 模型、GNS 模型。由表4 可知,成分3 和成分7 对PM2.5质量浓度产生了负影响;而成分3 和成分7 表明环境的治理能力越强、城市污染度越低,PM2.5质量浓度会降低;而成分2、成分4 和成分6 给PM2.5质量浓度带来了很大的正影响,这些成分主要为工业污染因素、城市空间结构因素、环境污染因素,因此政府应该减少工业污染,提高城市空间结构的合理性,提高环境治理能力。
赤池信息准则(Akaike Information Criterion,AIC)和贝叶斯信息准则(Bayesian Information Criterion,BIC)通常用于判别模型的优劣,其值越小表示模型的拟合效果越好,得到每个模型的AIC、BIC 值如表5所示。最后为了判别模型的空间依赖性,得到模型残差的空间依赖性检验结果如表6 所示。

表5 模型拟合效果对比

表6 模型残差的空间依赖性检验
式(12)(13)中:k为模型参数个数;L为似然函数;n为样本数量。
在最小二乘法中,似然函数为:
在SLM 模型中,似然函数为式(14)。
在SEM 模型中,似然函数为式(15)。
在SDM 模型中,似然函数为式(16)。
在SDEM 模型中,似然函数为式(17)。
在GNS 模型中,似然函数为式(18)。
由表5 可知,SDEM 模型的AIC 和BIC 值最小,GNS 模型的AIC 值和BIC 值次之,可见SDEM 模型的拟合效果是6 个模型中拟合效果最好的。此外,根据表6 的结果,OLS 模型残差都具有显著的空间正相关性,而考虑了PM2.5质量浓度具有空间依赖性的SLM、SEM、SDM、SDEM、GNS 回归模型则在一定程度上削弱了这种空间相关性的影响。因此在上述6个模型中,考虑了PM2.5质量浓度的空间效应的空间杜宾误差模型效果是最优的。
4.2.3 PM2.5质量浓度影响因子分析
根据表4 中SDEM 模型结果,主成分2、主成分4、主成分6 对PM2.5的质量浓度都产生了显著的正相关性,而主成分2、主成分4、主成分6 里所包含的主要因素有工业二氧化硫排放量、工业二氧化氮排放量、工业烟尘排放量、城市建设用地面积、可吸入颗粒物浓度、第二产业数目、工业数目,这些因素都会影响城市PM2.5质量浓度,因此政府应该控制城市中工业废气、烟尘的排放量,对排放的废气中的污染物含量进行实时监控,对于超出国家标准排放废气的工厂进行罚款等处理;其次,城市应该对建设用地进行合理规划,尽量合理利用城市的空间结构;城市为了发展经济,可能会不断引入企业,政府应该合理管控城市企业的数目、企业的类型,多引入科技开发型企业,减少污染类企业的入驻。
主成分3 和主成分7 对PM2.5质量浓度产生了显著的负相关作用,包含的主要因素有污水处理率、生活垃圾处理率、绿化覆盖率、第三产业数目等,政府应该提高城市污水、垃圾处理率,呼吁市民保护环境,增加城市的绿化带,适当提高第三产业数目及服务业数目。
综合上述分析,只有管控影响PM2.5质量浓度的相关因子,才有利于控制城市空气污染物质量浓度。
5 结论
本文通过构建空间回归模型对2020 年空气污染物PM2.5进行了时空分布特征及集聚特征分析,采用主成分分析法提取出反映原始数据大部分信息的因子,再利用OLS 模型、OLS 模型、SLM 模型、SEM 模型、SDM 模型、SDEM 模型、GNS 模型构建出了PM2.5质量浓度模型。
主要研究结果如下:①在中国,城市空间结构、社会经济及环境及其交互作用会对PM2.5质量浓度产生明显影响。通过主成分分析法,将20 个因素降维成7 个主要因素,在这7 个因素中,对PM2.5质量浓度产生负相关的因素有主成分3 和主成分7,而主成分1、主成分2、主成分4、主成分5 和主成分6 对PM2.5质量浓度产生了极大的正影响,因此政府在空气污染治理过程中,首先应该呼吁人们保护环境、减少工业污染量,对工业废气、废水、生活垃圾等进行处理,呼吁市民保护环境,爱护环境;其次应该合理利用和设计城市空间结构。②本文比较了OLS 模型、SLM 模型、SEM 模型、SDM 模型、SDEM 模型、GNS 模型,发现SDEM 模型是6 个模型中拟合效果最好的,且OLS模型残差具有显著的空间正相关性,而其他回归模型则在一定程度上削弱了空间相关性的影响。
