圆柱形装药不确定爆炸作用下钢管RPC柱的破坏机理*
2023-06-01马建军陈建营陈万祥薛海恩许正阳
马建军,陈建营,陈万祥,2,3,薛海恩,许正阳
1.中山大学土木工程学院,广东 珠海 519082
2.陆军工程大学爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007
3.南方海洋科学与工程广东省实验室,广东 珠海 519082
活性粉末混凝土RPC(reactive powder con‐crete)是一种高强度、高耐久性和稳定性良好的超高性能混凝土(Richard et al.,1995)。实际应用中,RPC 表现出明显的脆性,呈突然爆裂式破坏,限制了其工程应用(蔡绍怀,2007)。钢管RPC 是将RPC 填充于钢管中形成的一种组合构件,因抗压强度高、塑性性能和抗震性能优异(钟善桐,2006),已被广泛用于重要目标的承重构件。
冯红波等(2007)分析了比例距离为1.0 m/kg1/3时钢管混凝土柱的破坏特性;崔莹等(2015)对复式空心钢管混凝土柱进行了抗爆试验;Wang et al.(2017)考虑钢管厚度、截面形状等的影响,发现在近距离爆炸作用下钢管混凝土仍能保持大部分的轴向承载力。Fujikura et al.(2008)针对多种爆炸荷载下桥梁中的钢管混凝土墩柱的破坏形态进行了试验;Bambach et al.(2011)对钢管混凝土构件在横向冲击下的响应进行了试验研究和理论分析;Remennikov et al.(2014)对方形钢管构件进行了接触爆炸和近距离爆炸试验,并提出了方形钢管挠度的预测方法。Chen et al.(2019)综合考虑结构阻尼、轴向力作用及温度效应的影响,对火灾后钢管RPC 柱的爆炸损伤情况和损伤评估方法进行了研究;Zhang et al.(2020)发现增加钢管厚度可有效提高节段式钢管混凝土柱的抗爆能力;李国强等(2013)得到了钢管混凝土柱上迎爆面与背爆面的冲击波压力时程曲线、压力分布形式等。
但以往研究多是特定比例爆距下结构本身的动态响应,对装药形状及起爆方式的影响却鲜有报道,且球形装药、起爆点的数量及位置也常被忽略(Wilkinson et al.,2013;Cormie et al.,2013)。本文利用LS-DYNA 软件对圆柱形装药在近距离爆炸下的反射超压峰值进行分析,建立不确定爆炸荷载模型,并对不确定爆炸作用下钢管RPC 柱的动力响应和破坏机理进行了探讨。
1 数值模拟及试验验证
1.1 试验方案与材料参数
钢管RPC 柱抗爆试验在陆军工程大学野外试验场进行。钢管RPC 柱尺寸厚度t、外径ϕ、长度L分别为6、194、2 500 mm。钢管采用Q345 无缝钢管,厚度为6 mm,外径为194 mm。抗爆试验装置中,炸药中心至钢管RPC 柱表面的距离为1 500 mm,比例距离为0.58 m/kg1/3,利用氮气高压气缸对钢管RPC柱施加754 kN的轴向力(轴压比为0.24)。在钢管RPC柱高度方向的钢-混凝土基座一侧均匀布置压力传感器,试件底部均匀布置位移传感器,以记录爆炸超压和结构挠度。
1.2 有限元模型及边界条件
利用LS-DYNA 软件建立钢管RPC 柱有限元模型,如图1所示。采用solid164单元进行网格划分,仅建立1/2 模型。模型的对称界面施加法向约束,基座表面施加全约束,以模拟钢管RPC 柱的实际约束情况。钢管与核心RPC 采用固连接触,利用关键字*AUTOMATIC_SURFACE_TO_SURFACE进行定义。采用动力松弛法对柱端施加恒定的轴向荷载,待荷载施加稳定后,施加爆炸荷载进行瞬态分析。

图1 钢管RPC柱有限元模型Fig.1 Finite element model of RPC-FST column
1.3 材料模型
本文采用K&C 材料模型描述结构在爆炸荷载作用下的动力行为,材料参数见表1(陈万祥等,2017)。K&C材料模型引入初始屈服面、极限强度面和残余强度面3个失效面,分别描述混凝土的初始屈服强度Δσy、极限强度Δσm及残余强度Δσr的变化规律,并考虑了材料的强化效应、损伤效应和应变率效应。其中

表1 RPC材料模型参数1)Table 1 RPC material model parameter
式 中a0y、a1y、a2y、a0、a1、a2、a1f和a2f为 屈 服 面特征参数;静水压力P= −(σ1+σ2+σ3)/3。不同的应力状态下,混凝土失效面发生变化,在给定的3个失效面中发生迁移。变化过程满足
式中η为强度参数,与有效塑性应变因子有关,且0 ≤η≤1。当混凝土处于拉-压状态时,损伤变量λ为

混凝土处于三轴受拉状态时,只发生体变,偏应变eij= 0,λ= 0。考虑该状态下的损伤情况,引入变量Δλ=b3fdkd(εv−εyv),此时
其中b3为考虑体积应变损伤的相关参数;fd为动态应力强度;kd为标量乘子;εv为体积应变;εyv为屈服体积应变。钢管和两端的钢板采用3 号模型(*MAT_PLASTIC_KINEMATIC)进行描述,其参数见表2(陈万祥等,2017)。

表2 钢材材料模型参数1)Table 2 Steel material model parameter
1)引自陈万祥等(2017)。
1)引自陈万祥等(2017)。
1.4 爆炸荷载简化
参考Hu et al.(2018),本文对结构施加阶梯式爆炸荷载作用,如图2所示。计算时,将爆炸荷载简化为三角形荷载,具体加载形式为

图2 等效荷载示意图(单位:mm)Fig.2 Schematic diagram of equivalent load (unit:mm)
式中Pmax为超压峰值;t为作用时间,T+为正压作用时间。近距离爆炸中,地面刚性反射超压与入射超压基本相等,Pmax取入射超压的2.0 倍。T+采用 Henrych(1979)提出的经验公式,即
式中Z为比例距离;W为炸药装药量。
Fujikura et al.(2008)引 入 折 减 系 数β(0.38~0.85)以考虑冲击波绕射、非规则反射及清除效应的影响。基于圆截面墩柱爆炸试验结果,取圆截面上的有效爆炸超压等于作用在平面上的有效爆炸超压的0.45 倍。因此,爆炸荷载的表达式修正为
其中P3、P2、P1为反射超压峰值实测值。
1.5 计算结果对比分析
陈万祥等(2017)的试验结果表明,在比例距离为0.58 m/kg1/3的近距离爆炸荷载作用下,钢管RPC 柱D1、D2 和D3 测点的最大位移分别为14.65、28.60 和38.15 mm,残余位移分别为1.86、3.64 和4.68 mm,构件整体破坏模式呈弯曲破坏。3 个测点位移时程曲线的模拟与试验结果对比,如图3所示。可以看出,计算位移在极短时间内达到峰值,且与试验结果基本一致;振动频率逐渐减小,并围绕某一数值上下波动,直至稳定。

图3 位移时程曲线Fig.3 Displacement time-history curves
图4为钢管RPC柱实际破坏形态与损伤云图对比,可见柱整体变形较小,塑性应变主要集中于支座附近和跨中部位。

图4 钢管RPC柱破坏形态及损伤云图Fig.4 Failure appearances and damage contours of RPC-FST column
由表3可以看出,最大位移的模拟结果与试验结果吻合较好,残余位移的数值模拟结果稍大,但随着距跨中位置的距离增大,两者之间的差距不断减小,其原因是在试验过程中,爆炸冲击波经过钢管RPC 柱表面时发生绕射,致使冲击波在柱表面呈非均匀分布,且经过柱体的冲击波遇地面后反射,对柱整体的弹性恢复起到一定的干扰。此外,本文的数值模拟方法忽略了爆炸负压的影响,导致残余位移的计算结果大于试验结果。

表3 试验结果与数值模拟结果对比Table 3 Comparison of experimental results and numerical results mm
2 近距离爆炸荷载不确定性模型
2.1 有限元模型
研究发现(ASCE,2011),炸药形状、起爆点位置和炸药放置方位对近距离爆炸(比例距离Z<1.2 m/kg1/3)冲击波作用有显著影响。图5 为近距离爆炸荷载不确定性分析有限元模型,其中圆柱形装药质量为 1 kg,长径比L/D分别为1.0、1.5、2.0、2.5、3.0。圆柱形装药分别选取轴向与径向两端的中点,以及炸药的中心点为起爆点,并收集炸药轴向与径向两个方向的反射超压数据。

图5 有限元模型Fig.5 Finite element model
参考Fujikura et al.(2008)的分析方法,先建立刚性地面条件下,炸药空中起爆,获取指定测点处的反射超压峰值数据,然后将修正后的反射超压峰值作用于钢管RPC 柱迎爆面进行动力响应分析。如图5 所示,3 个测点分别为P3、P2、P1,两点之间的间隔为415 mm,且各测点处均设置了50种工况。
2.2 网格收敛性分析
为保证数值模拟的可靠性和计算精度,进行网格收敛性分析,并将计算结果与现有预测公式(Brode,1959;Baker,1973;Henrych,1979;Tolba,2001)进行对比。根据方秦等(2003)给出的入射超压与反射超压的换算关系,计算各经验公式的反射超压峰值。选取5、6 和10 mm 的网格来进行网格收敛性分析,如表4 所示。图6 给出了数值模拟与经验公式计算的反射超压峰值结果。通过对比发现,在比例距离范围为0.4 ~ 0.8 m/kg1/3时,单元网格为6 mm 的模拟结果与经验公式计算结果吻合较好,单元网格为5 mm 和10 mm 的模拟结果分别相对偏大和偏小。因此,本文将采用6 mm 的单元网格进行近距离爆炸荷载的不确定性分析。

表4 反射超压峰值结果对比Table 4 Comparison of peak reflected overpressures
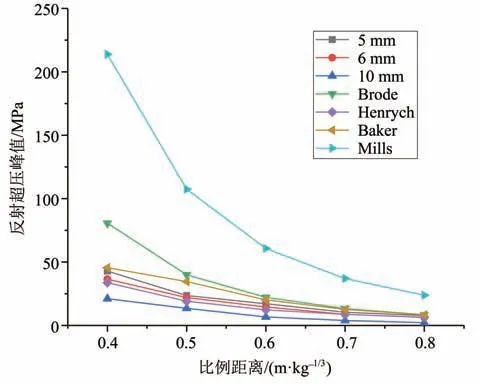
图6 反射超压峰值结果对比Fig.6 Comparison of peak reflected overpressures
2.3 不确定性模型的建立与统计分析
随机爆炸荷载计算结果(Low et al.,2001;Bogosian et al.,2002;Netherton et al.,2010)表明,爆炸荷载的反射超压峰值符合正态分布。本文利用Origin 软件对3 个测点不同比例距离下的数值模拟结果进行正态分布检验,并将模拟结果进行统计分析,选取合适的反射超压峰值进行3阶多项式拟合,建立近距离爆炸荷载不确定性模型。
正态分布检验采用Shapiro-Wilk 检验(也称W检验),计算公式为
式中
m=(m1,…,mn)T,m1,…,mn为标准正态分布随机变量的有序独立同分布的期望值,V为有序统计量的协方差;为样本均值。
式中y0为直流偏置项;xc为峰值;w取高斯分布曲线半高宽的0.849 倍;A为曲线下与直流偏置项之间的总面积。
利用Gauss 方程对不同比例距离下的数据进行非线性曲线拟合,结果如图7 所示,3 个测点模拟结果均服从正态分布。选取了数值模拟结果的平均值和最大值(表5)来进行不确定性分析,建立不确定性模型。

表5 不同比例距离下反射超压峰值平均值与最大值Table 5 Average and maximum value of peak reflected overpressure for different scaled distances

图7 不同Z值下的反射超压峰值频率分布直方图Fig.7 Frequency distribution histogram of peak reflected overpressure with different Z
取反射超压峰值的平均值作为代表值,3 个测点处的反射超压峰值拟合式分别为

取反射超压峰值最大值作为代表值,3 个测点的反射超压峰值拟合式分别为

3 不确定爆炸作用下钢管RPC 柱动态响应分析
3.1 最大位移和残余位移
将不确定性模型选取的代表值(平均值和最大值)作用于钢管RPC 柱进行数值模拟。最大位移和残余位移的模拟结果如表6~7所示。可以看出,最大值为代表值的爆炸荷载对钢管RPC 柱作用产生的最大位移和残余位移较平均值大;并且随着比例距离的减小,最大位移和残余位移都明显增大;跨中部分的位移较其余部分大,并且随着离跨中部位距离的增大,最大位移和残余位移均明显减小。

表6 不同比例距离下的最大位移Table 6 Maximum displacements for different scaled distances

表7 不同比例距离下的残余位移Table 7 Residual displacements for different scaled distances
图8为钢管RPC柱的位移时程曲线(部分)。平均值为代表值的爆炸荷载作用下的钢管RPC 柱较最大值更快达到稳定;随着比例距离的增大,爆炸荷载逐渐减小,导致钢管RPC 柱的振动频率逐步增大,且各测点处的位移峰值也逐渐减小,但最大值为代表值时的位移峰值均大于平均值;最大值为代表值的各测点处均具有一定的残余位移,说明这些工况下钢管RPC 柱发生一定程度的塑性变形。对比平均值为代表值的工况,平均值为代表值时的各测点处随时间的推移,基本恢复至原始状态,尤其是D1 测点处,说明这些工况下钢管RPC柱基本处于弹性变形阶段。

图8 不同Z值下的钢管RPC柱位移时程曲线Fig.8 Time-history curves of displacement for RPC-FST column subjected to blast loading with different Z
定义相对位移r=Dr/L,Dr为跨中残余位移,L为钢管RPC 柱的长度。根据蔡绍怀(2007),当构件的相对位移r> 2%时即进入屈服状态。计算表明,各工况下钢管RPC 柱的相对位移均小于2%,均未发生屈服破坏,表现出良好的抗爆性能。
分析表明(方秦等,2003),爆炸荷载作用下的梁柱结构可能出现弯曲破坏、弯剪破坏和直剪破坏。图9为钢管RPC柱有效塑性应变云图,可以发现:塑性应变主要集中在跨中部分和支座附近位置;且随着比例距离的减小,有效塑性变形逐渐增大,支座附近的塑性应变梯度及作用范围明显增大。

图9 不同Z值下的钢管RPC柱有效塑性应变Fig.9 Effective plastic strain for RPC-FST column subjected to blast loading with different Z
最大值作用下的钢管RPC 柱的有效塑性应变大于平均值,且在同一比例距离时,具有较为明显的差别;对于柱体的变形形态,最大值作用下,柱体跨中部位有明显的弯曲变形,随着比例距离减小,支座附近的应力梯度增大,柱构件出现剪切变形。当应力梯度足够大时,可能会出现剪切变形先于弯曲变形的情况,容易导致柱构件的脆性直剪破坏;而平均值作用下,柱体有较小的弯曲变形,随着比例距离的增大,柱体变形减小,有效塑性应变的作用范围也明显变小。
3.2 不确定性分析
对以平均值和最大值为代表值的爆炸荷载作用下的钢管RPC 柱的动力响应进行分析,可以发现:两种统计作用方式之间存在较大的差异。以平均值为代表值的爆炸荷载对柱体的作用效应较小,结果也相应地较为保守。而以最大值为代表值时,柱体产生的变形和位移都相对较大,明显影响钢管RPC柱的抗爆性能。
考虑到爆炸荷载的不确定性和爆炸发生时产生的急剧破坏性,为确保能更全面地考虑各种突发情况,保证钢管RPC 柱具有足够的抗爆性能,需要考虑炸药的装药形状、放置方位和起爆点的位置。因此,本文建议选取最大值作为不确定性分析的代表值,通过预测模型确定最大的爆炸荷载,进而对结构进行动力分析,判别结构的工作状态。
4 结 论
1)采用突加线性荷载的等效形式来代替爆炸荷载作用于钢管RPC 柱,将数值模拟结果与试验结果对比。结果表明:3 个测点的最大位移模拟结果都与试验结果吻合较好,残余位移存在一定的差距,其原因为等效荷载作用忽略了地面反射超压和负压对构件动态响应的影响。
2)采用圆柱形装药时,考虑炸药放置方位、长径比和起爆点3个变量,对爆炸荷载(反射超压峰值)进行统计分析,建立爆炸荷载的不确定性模型。经正态分布检验,在3个测点处的反射超压峰值均符合正态分布。
3)以爆炸荷载的平均值和最大值为代表值作用于钢管RPC 柱进行数值模拟。结果表明,钢管RPC 柱具有良好的抗爆能力,有效塑性应变主要集中于跨中和支座附近,并随着比例距离的减小,塑性应变增大,支座附近塑性应变梯度明显增加。最大值为代表值作用下的钢管RPC 柱最大位移和残余位移均远大于平均值为代表值得到的计算结果。
4)基于平均值和最大值为代表值的钢管RPC柱动态响应差异显著。出于安全考虑,本文建议采用统计爆炸荷载的最大值对圆柱形装药近距离(Z= 0.4~0.8 m/kg1/3)爆炸作用下钢管RPC 柱的动态位移进行预测。
