双边定时截尾下广义Pareto 分布的可靠性分析*

张峰源，蔡 静，罗君念

（贵州民族大学，贵阳 550025）

0 引言

在产品的寿命试验中，受时间、经费的限制，通常会采用截尾的方式进行寿命试验。由于广义Pareto 分布在工程科学、处理医学等方向的寿命实验中起着极其重要的作用，已有很多研究者对广义Pareto 分布的性质进行深入研究。CHENG 等研究了在循序-I 型删失数据下广义Pareto 分布参数的极大似然估计和EM 算法估计［1］；邢务强等研究了I型混合截尾下指数- 威布尔分布参数的极大似然估计和经验Bayes 估计［2］；侯华蕾等研究了Pareto分布可靠性参数的Bayes 估计［3］；龙兵等研究了定时区间删失样本下指数分布的竞争失效问题［4］；HANICH 等讨论了逐步首次失效截尾下广义Pareto分布的参数估计［5］；葛露娟等研究了在不同删失情况下广义Pareto 分布形状参数的Bayes 估计［7］；OKASHA 等研究了逐步II 型截尾数据下的广义Pareto 分布的E-Bayesian 估计问题［8］；赵旭等研究了三参数广义Pareto 分布的最小二乘估计［9］；龙沁怡等对广义Pareto 分布在I 型删失数据下的形状参数进行极大似然估计［10］。

双边定时截尾试验是在事先规定的时间开始试验和停止试验，为了不使失效数过少或过多，恰当地规定试验停止时间是实施定时截尾寿命试验的关键。但是在双边定时截尾下运用不同方法对广义Pareto 分布的可靠性估计文献较少，本文基于极大似然估计、EM 算法、Bayes 估计研究了双边定时截尾数据下广义Pareto 分布的参数估计和可靠性指标估计问题，并比较各方法在不同样本数据下的估计精度。

设随机变量X 服从广义Pareto 分布，分布函数为：

1 模型描述与极大似然估计

将式（2）、式（3）代入式（4）则似然函数表达式为：

2 EM 算法

下面用EM 算法求解。

3 近似置信区间

LOUIS 在应用EM 算法时提出了一种提取观测信息的方法，观测的Fisher 信息可以用来构造渐近置信区间［11］。

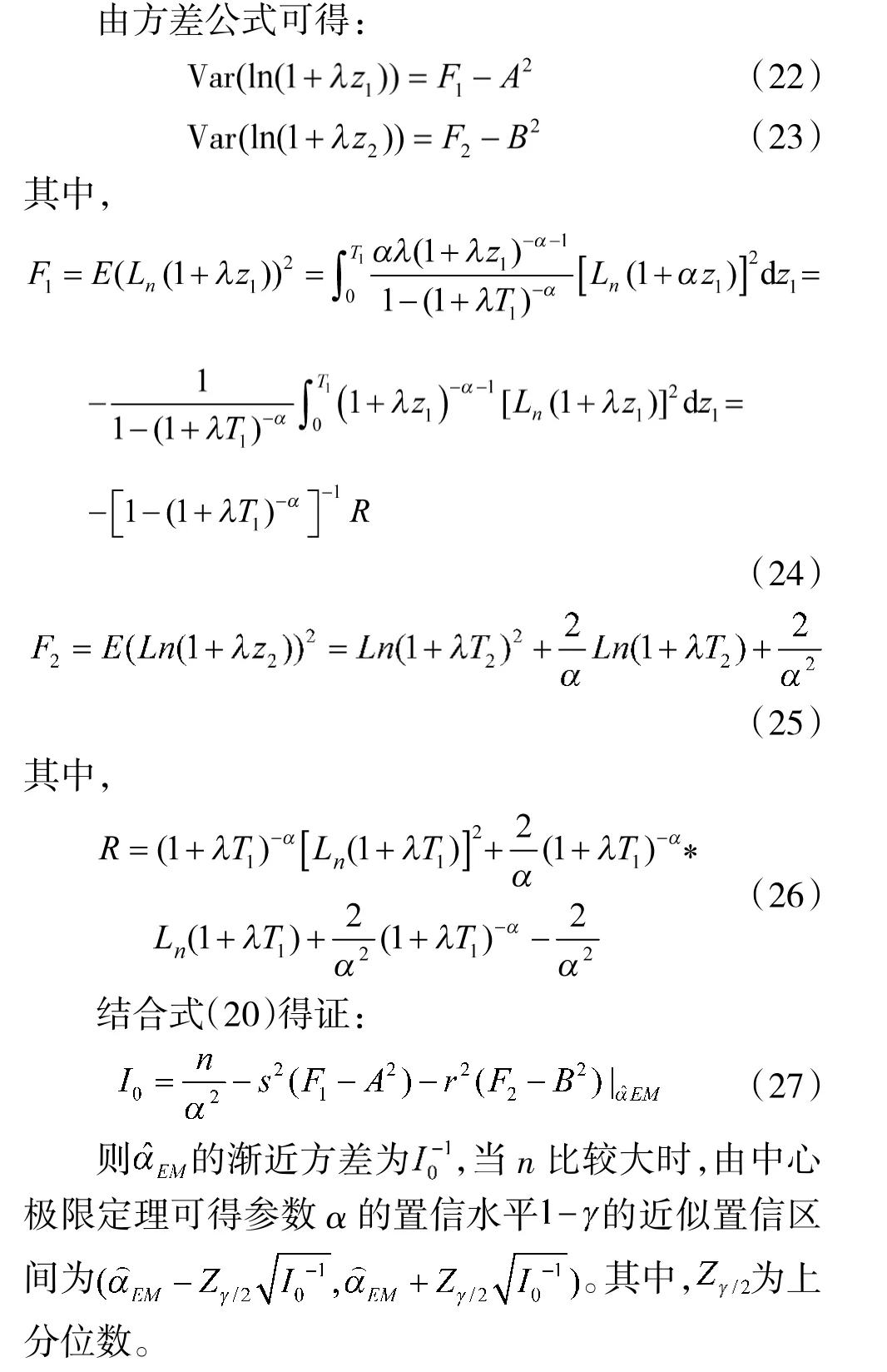
4 Bayes 估计

取参数α 的先验分布为无信息先验分布：

5 数值模拟

为了研究样本量和截尾时间对估计精度的影响，给定样本量n，截尾时间T1、T2，参数=0.5、α=2.05。生成双边定时截尾广义Pareto 分布数据步骤如下：

区间估计的上、下限与渐近方差模拟结果见表3 所示。

由表1～表3 看出：1）在小样本情况下，EM 估计与Bayes 估计的效果较好，随着样本量的提升，Bayes 估计的效果有明显提升，优于极大似然估计；2）EM 算法在任意样本条件情况下，估计效果都较为稳定，且在小样本情况下优于极大似然估计和Bayes 估计；3）随着左截尾的时间越短，极大似然估计与Bayes 估计的准确度越高；4）对可靠度进行估计时，极大似然估计比EM 算法和Bayes 方法更精准。

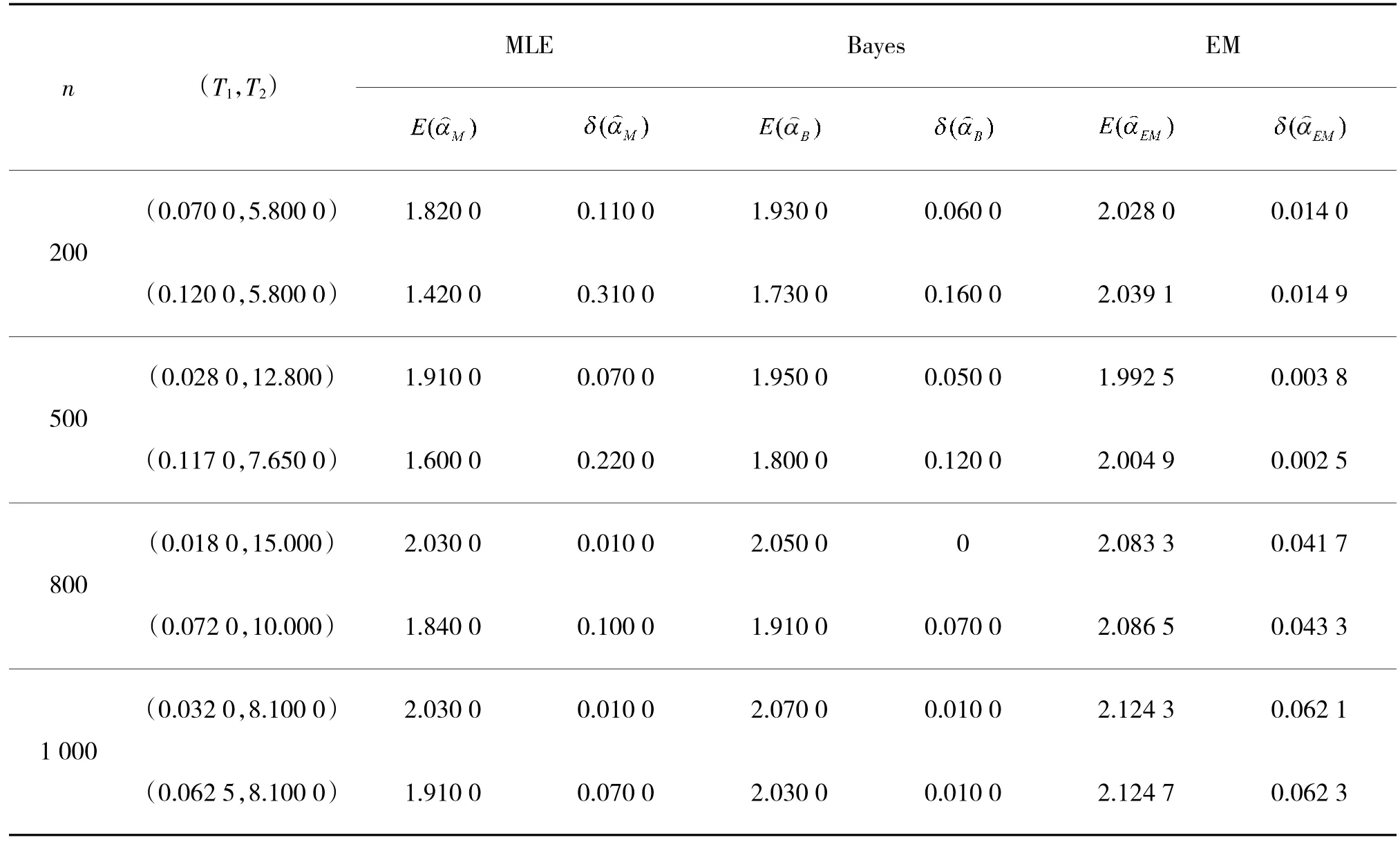
表1 参数的估计值与平均相对偏差Table 1 The estimated value of the parameter deviates from the average relative deviation

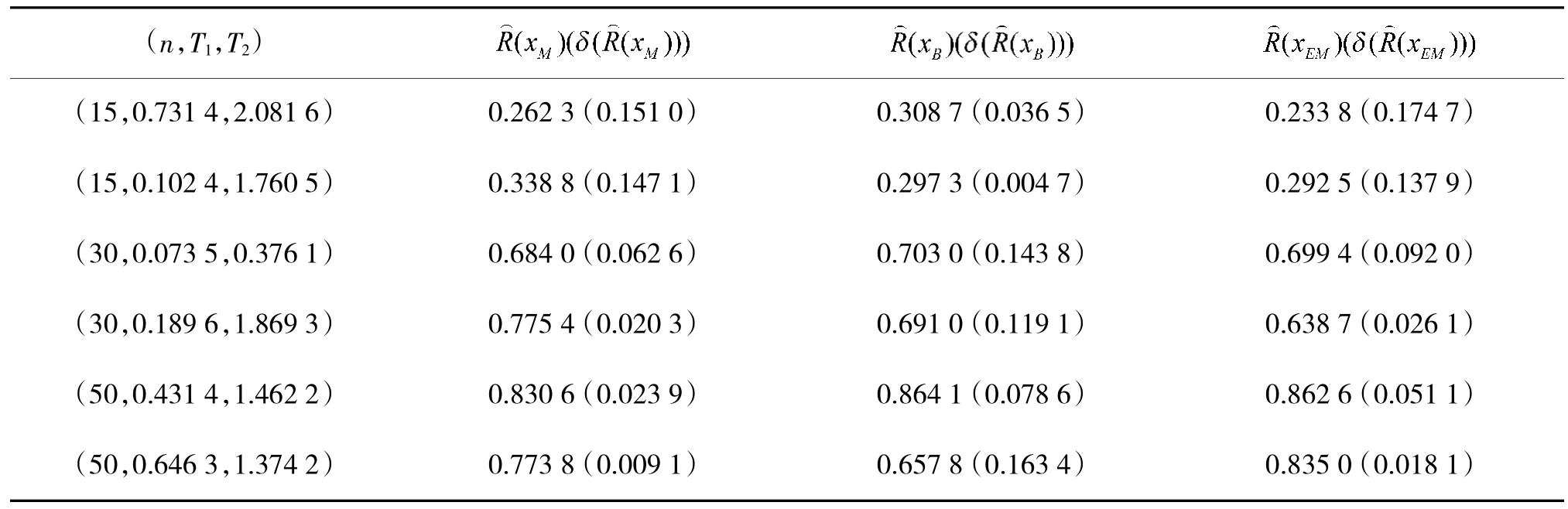
表2 可靠度R 的估计与平均相对偏差R（10）Table 2 The estimation of reliability R is relative to the mean deviationR（10）

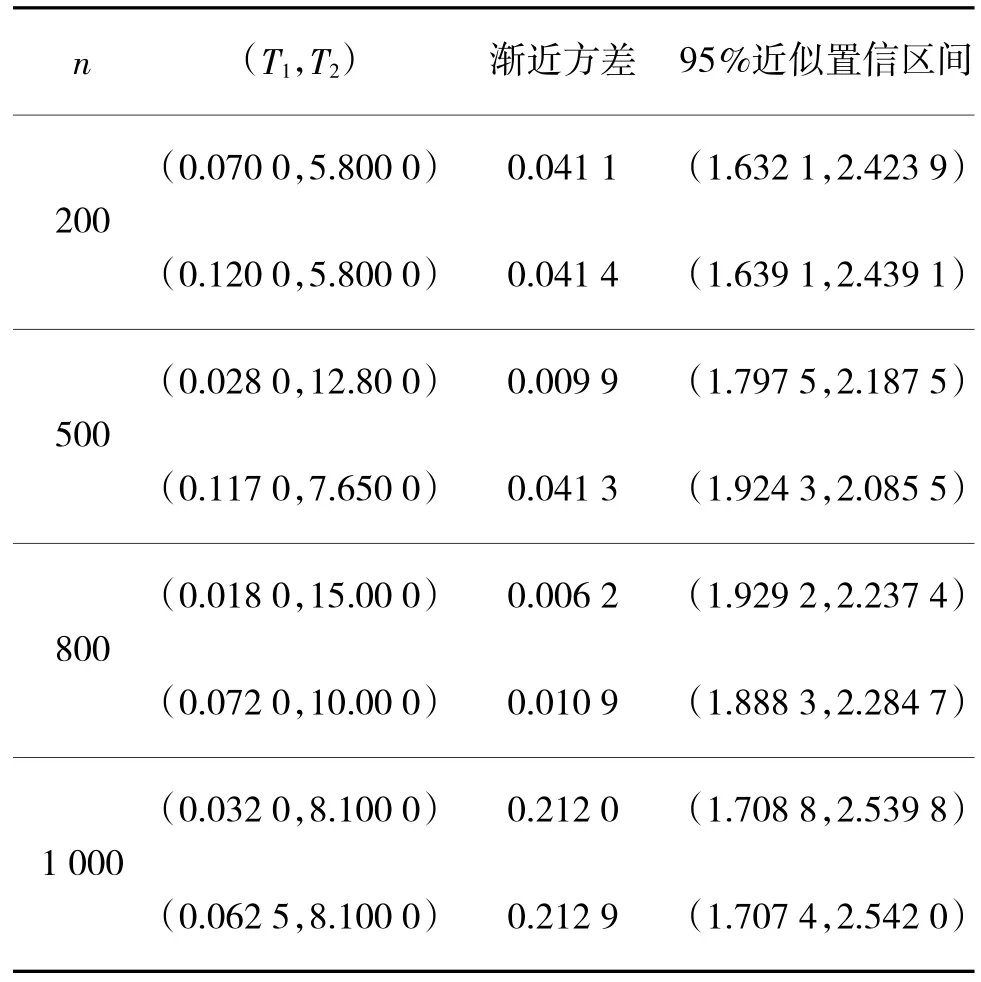
表3 EM 算法区间估计Table 3 EM algorithm interval estimation

6 结论

在双边定时截尾样本下，估计广义Pareto 分布的形状参数时，应根据样本量的大小选取不同的估计方法。在样本量较小时，采用Bayes 方法和EM 算法比极大似然法给出的估计有较小的平均相对偏差；在样本量较大时，采用极大似然估计法和Bayes方法比EM 算法给出的估计有较小的平均相对偏差。当选用极大似然估计法和EM 算法时，可靠度R的估计可达到很高的精度。