常见情形下同类铜币的视觉相似度分析

程冠桦,张俊然,黄江涛

(1. 四川大学电气工程学院,四川 成都 610065;2. 南宁师范大学计算机与信息工程学院,广西 南宁 530001;3. 四川大学“医学+信息”中心, 四川 成都 610065)

1 引言

文物和艺术品的识别、分类与鉴定等需要相关专业人员进行初步整理,但由于人工观察具有一定的个人主观性,对于一些复杂情况往往无法定量且有效地作出判断[1]。计算机视觉技术发展日趋成熟,已广泛应用于人脸、车牌识别等领域。对于文物的识别、分类与鉴定来说,相比人工的主观经验判断,利用计算机视觉方法对文物及艺术品实现定量分析,可避免由于主观标准不一而导致的认知偏差。如文献[2]通过比较待测印鉴与标准印鉴的多种统计参数对印鉴进行真伪鉴别。文献[3]通过提取检验笔迹与参考笔迹的局部纹理特征实现字迹鉴定。文献[4]采用GIST特征描述子表达书体特征,并结合SSC相似性敏感编码算法,根据海明距离实现书法字体的定量识别。文献[5]利用马尔可夫随机场对国画的真伪进行定量分析。文献[6,7]利用文物轮廓以及灰度共生矩阵纹理特征等指标,定量地对文物图像进行辨识与鉴定。文献[8,9]分别利用小波神经网络、形状和纹理信息对瓷器文物定量地进行等级定级、真伪识别以及年代识别。

就铜币而言,在对其进行整理分类的初筛过程中,发现由于受保存环境差异或制作批次不同等因素的影响,同类铜币所呈现出的表面状态不尽相同[10]——保存在温湿度和酸碱度适中环境里的铜币表面特征清晰,而其余长期暴露在空气或其它潮湿环境中的铜币,受氧化发黑或是表面生成铜锈,破坏了纹理图案的清晰度;此外,不同批次制造出的铜币也存在细微差异。由于同类铜币存在着不同的复杂情形,人工判断容易受到干扰,因此在整理分类时需要定量的标准以确保同类铜币能够被正确识别。

针对以上复杂情形导致人工观察无法定量评判同类铜币这一问题,本文提出基于SURF (Speeded Up Robust Features)特征[11]对待测铜币与标准铜币进行相似计算,从而定量地识别出同类铜币。具体通过构建多尺度空间结构保证特征具有尺度不变性,定位关键点主方向保证特征具有旋转不变性,结合关键点邻域区域信息保证特征描述子的一般性和信息完整性,对两特征描述符按照轮流主次的计算策略保证结果的唯一性,最终在特征点空间上计算相似性,通过相似得分识别出同类铜币。实验表明,通过对各铜币提取的128维SURF特征进行相似度计算,能够很好地识别出不同情形的同类铜币。

2 特征提取

为了使获得的铜币特征具有尺度不变性、旋转不变性、一般性和代表性,其提取步骤包括构建多尺度空间、确定关键点以及特征描述。

2.1 Hessian矩阵

通过Hessian矩阵寻求铜币中稳定的突变点,而在构建之前需要先对图像进行滤波以消除噪声干扰。Lindeberg等人[12]证明高斯卷积核是实现尺度变换的唯一线性核,因此选用高斯滤波器保证特征具有尺度不变性。式(1)和式(2)分别为滤波运算与高斯核表达式

L(x,y,σ)=I(x,y)*G(x,y,σ)

(1)

(2)

其中I(x,y)为像素矩阵,L(x,y,σ)即为高斯滤波生成的图像,在此基础上构建Hessian矩阵

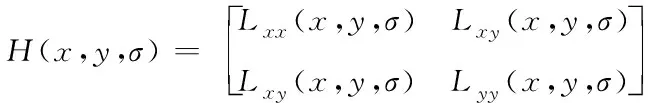
(3)

从式(3)可见Hessian矩阵由滤波图像在x和y方向的二阶偏导数构成,用以描述铜币的局部曲率信息。式(4)为Hessian矩阵判别式,通过判别式符号初步确定该点是否为铜币的局部关键点

det(H)=Lxx×Lyy-Lxy×Lxy

(4)

由于获取关键点需先进行高斯滤波,再对滤波图像二次求导,过程较为繁琐;为了提高效率,采用图1的盒式滤波器[11]近似代替高斯滤波器,将滤波计算转换为了像素和的加减运算过程,从而用式(5)近似式(4)寻求关键点,

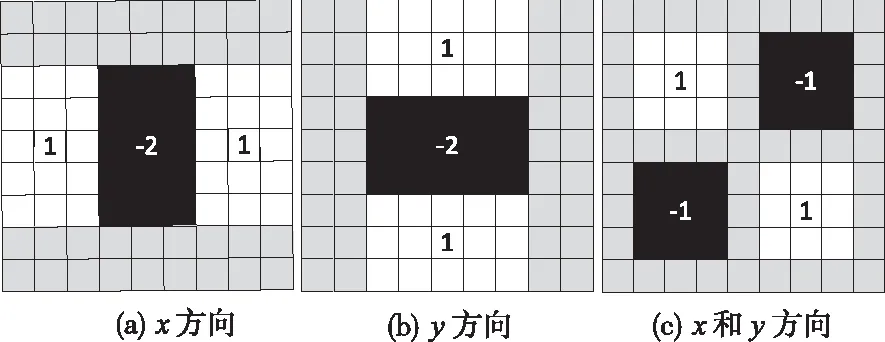
图1 三个方向的盒式滤波器示意图

det(H)=Dxx×Dyy-(ω×Dxy)2

(5)

式中Dxx,Dyy和Dxy分别为原图像经三个方向盒式滤波后的响应值,ω为加权系数,用以平衡近似计算产生的误差。

2.2 多尺度特征提取

为了保证铜币特征不受尺度变化影响,对此构建多尺度空间寻求在不同尺度下均稳定的特征点——通过调整盒式滤波器大小生成不同尺度的图像,从而构建多尺度金字塔。尺度空间由若干组图像组成,其中同组图像为同一输入经过尺寸依次增大的盒式滤波生成的一系列响应图。

完成多尺度空间的构建后,计算多尺度结构中的极值点进行关键点筛选。图2为关键点邻域示意图——包括同尺度图像内的8个邻域点和相邻尺度对应位置的18个点。在筛选过程中,将每个检测点与其邻域内的26个点进行大小比较,确保关键点在整个尺度空间内均为极值点,从而保证所提取特征的稳定性和高鲁棒性。

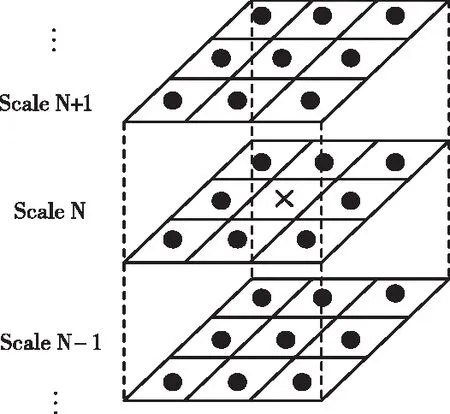
图2 关键点邻域示意图

如图3所示,以上步骤得到的为尺度空间中的离散极值点,为了获取特征点的准确位置,需要进行曲线拟合。

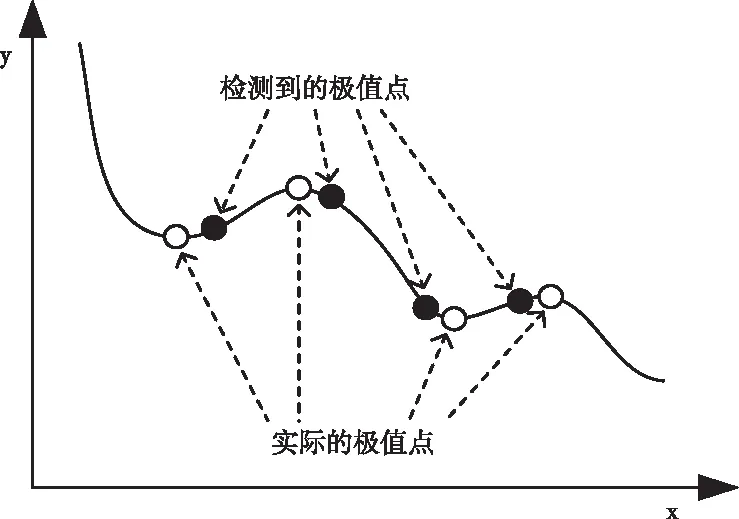
图3 曲线拟合极值点

利用Taylor展开式拟合函数,

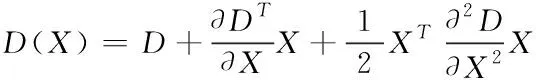
(6)

对式(6)求导,并令其等于0,有:

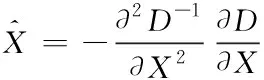
(7)

再将式(7)代回式(6),得到式(8):

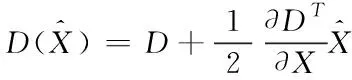
(8)

由于部分极值点响应较弱,应进行剔除,使获取的特征点更具稳定性。在本文中,若D()<0.03,则舍去对应的极值点X,反之保留为特征点。

2.3 特征描述

为了保证铜币特征不受旋转角度的影响,需要先确定特征点的方向。如图4所示,以特征点X为中心,6s(s为尺度空间值)为半径计算圆形范围内的Haar小波响应;再设置以X为顶点,张角为60°的扇形滑动窗口,以0.2弧度的步长旋转,依次统计窗口内Haar小波响应值的累加和,将最大累加值所对应方向确定为特征点X的主方向,同时将达到最大累加值80%以上的方向作为辅方向以增强鲁棒性。

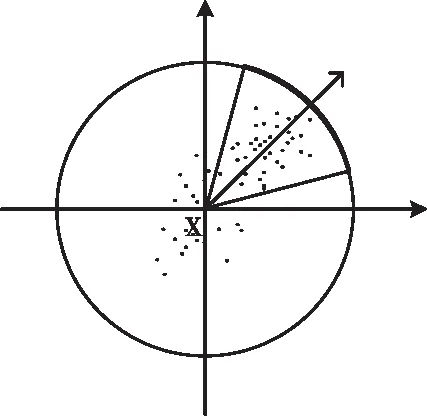
图4 确定特征点主方向

确定特征点方向后以主方向为基准进行特征描述——以特征点为中心,取边长为20s的正方形邻域,将其与主方向对齐后划分成4×4个子区域,分别统计各子区域内水平方向和竖直方向的Haar响应值。为了进一步增强特征点的独特性,使铜币特征具有更好的区分性,将小波特征继续进行细分:根据dy<0和dy≥0将dx与|dx|分别分为两部分进行加和计算,同理根据dx<0和dx≥0将dy与|dy|均分为两部分进行计算,如式(9)所示,每个子区域共包括8个分量。

V=(∑dx+,∑dy+,∑|dx+|,∑|dy+|,

∑dx-,∑dy-,∑|dx-|,∑|dy-|)

(9)

(10)

3 相似性计算

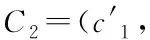
SIM(C1,C2)=SIM(C2,C1)

(11)

其中SIM(·)表示两特征描述符之间的相似度计算。本文选用余弦相似度[13]作为相似度量方式,且由于特征向量均已做归一化处理,实际计算过程只需进行内积运算。计算时分别将两铜币作为主比较位置以保证相似度的唯一性,具体过程如下:先将copper1中的特征点作为主比较对象,逐一寻求copper1每个特征在copper2中的K最近邻点,计算特征描述符在相应近邻点中的最大相似值,待copper1中所有特征点均完成相似度计算后,取相似平均值作为copper1与copper2的相似值;同理,再将copper2作为主比较对象,计算每一特征描述符与copper1的最大相似值,当copper2所有特征点均计算完毕后,取平均值作为copper2与copper1的相似值。最后将得到的两相似值按照特征数大小计算加权平均值,结果即为两铜币的最终相似度得分。公式如下

(12)

(13)

(14)

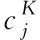
4 实验分析

实验中选用的铜币如图5所示,三组铜币分别对应同类铜币常见的三种情形,包括一组咸丰元宝、一组前苏联时期三分币和一组中华民国二分硬币:咸丰元宝组在视觉上几乎相同,除去极小部分杂质差异外,其形状、颜色、表面的文字以及其余绝大部分均表现一致,视觉上较易判断出该组铜币属于同一类别;前苏联硬币组的制造批次不同,表面图案存在小部分的细节差异,视觉上需进行仔细分辨才可做出判断;而在民国二分币组中由于铜币的保存环境等因素影响,各自表面存在较多杂质,差异较大,视觉上容易误认为该组铜币各自属于不同的类别。

图5 三种情形铜币

通过本文方法对三种情形的同类铜币进行相似度计算,实验中同时将128维SURF特征与SIFT[14]、Dense-SIFT[15]特征以及常规64维SURF描述子[11]进行效果比较,分析各特征对铜币的描述能力。如表1所示,可以看出各特征下三种情形的相似度均高于0.9,表明各方法均能够从状况复杂的铜币表面提取出强鲁棒性特征,并能对其进行稳定描述;此外,三种情形铜币的相似度结果依次减小,与视觉判断结果一致,表明了方法的真实有效性。相较而言,基于128维SURF特征的方法在各情形下的相似性计算得分均最高,表明其特征具有更强的描述能力,能够很好地识别出不同情形的同类铜币。

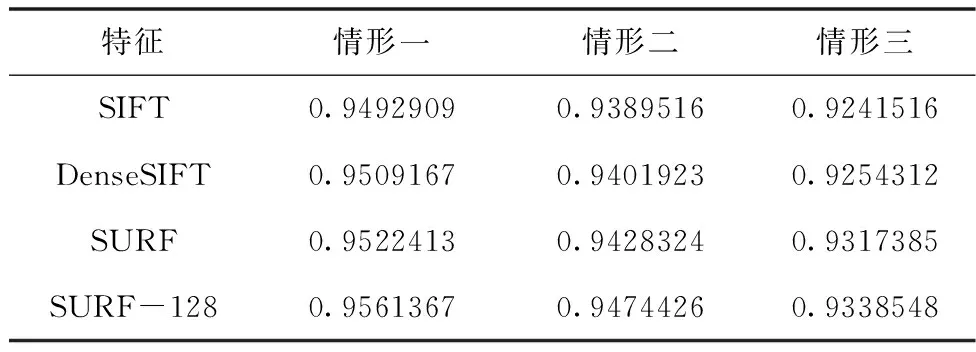
表1 不同特征下三种情形的相似度结果

为了进一步验证方法的有效性,将三种情形分别进行不同程度的旋转、亮度变化以及尺寸变化以模拟相似比较时的不同场景,分析各特征的表现效果。考虑铜币变换为相对关系,实验中选取铜币copper2进行依次变换。图6为各个变换示意图——(a)为亮度变换示意图,从左往右依次将亮度调整为原图像的0.5倍,1.5倍,2倍;(b)为角度变换示意图,依次将铜币按顺时针旋转45°,135°,270°;(c)为尺寸变换示意图,依次缩放为原图的0.5倍,0.8倍,1.5倍。

图6 三种变换示意图

图7为三种情形铜币在不同变换下四种特征描述子的相似度结果,其中横轴依次为不同程度的亮度、角度和尺寸变换,可以看出:在亮度变换下,四种特征均保持稳定水平,表明几种特征方法对亮度变化都具有较强的鲁棒性;而在旋转变换和尺寸变换下,DenseSIFT总体相似度呈现较低水平,表现最差,而其它三种特征描述子依旧保持稳定,表明具有较强的尺度不变性和旋转不变性,其中128维SURF描述子表现最为突出,在三种情形下均保持最高识别水平,再次证明其特征具有强大的描述能力。

图7 各特征在不同变换下的相似度表现

从表1和图7均可看出SURF-128效果更好,分析其原因:由于铜币表面纹理图案基本呈现为横纵向分布,相比于SIFT及DenseSIFT描述子依据梯度直方图生成,SURF-128描述子由水平及竖直方向Haar响应值组成,更能充分描述铜币特征的方向性变化;相比于常规64维SURF特征,SURF-128将小波响应值进一步细分,其描述子信息丰富度更高,故以此为特征能够更好地识别出同类铜币。

本文还探究了包括基于感知哈希算法pHash[16],图像灰度直方图[17]以及灰度共生矩阵GLCM纹理特征[7]的三种图像相似比较方法,并与本文方法进行分析比较。从表2可以看到,本文基于128维SURF特征的方法表现更为优异,能够更清晰地识别出同种铜币。

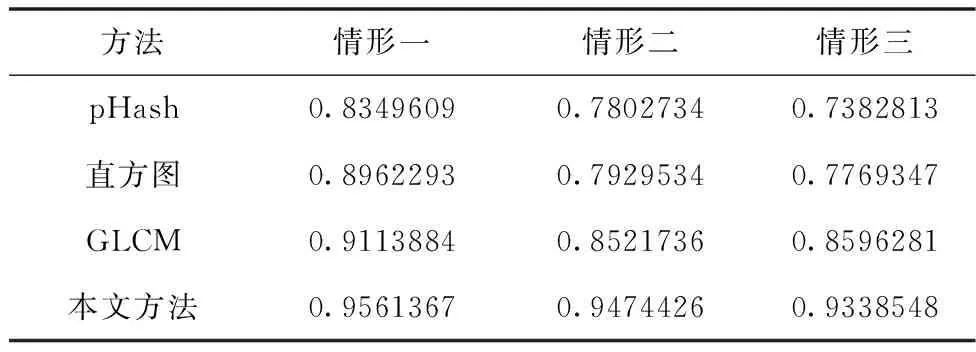
表2 四种相似比较方法的相似度结果

为了更好地比较方法的识别能力,实验还依次计算三组铜币两两之间的相似度,组成同类铜币组和不同铜币组,以验证方法对同类铜币的识别能力以及对不同铜币的区分能力。

如图8所示,各子图分别为使用感知哈希pHash、颜色直方图、GLCM纹理特征以及本文基于128维SURF描述子的相似度比较方法计算各铜币对的相似度结果热力图,其中横轴和纵轴上的c11和c12为图5中情形一的copper1和copper2,其余编号依此类推;热力图沿主对角线对称,各个方块即为相应铜币之间的相似度得分,颜色越深表示两铜币相似度越高。可以看出,图(a) (b)中颜色较为混乱,甚至出现同组铜币的相似度低于不同铜币相似度的情况,表明方法鲁棒性较差。图(c)中c21、c22与c31、c32之间颜色过于接近,分析原因发现其表面纹理分布情况较为类似,导致灰度共生矩阵统计情况相似,从而产生相似度较高的假阳性情况。而对于图(d),热力图对角线位置存在三组明显较深颜色的2×2方块,如c11和c12,c21和c22,c31和c32分别对应三种情形的同类铜币,其相似度得分均高于0.9,表明方法能够灵敏准确地识别出同组铜币;而图中其它方格颜色均较浅,其相似度得分为0.65以下,与同类铜币组的相似度得分相比差异明显,表明方法能够较好地区分出不同铜币。通过以上分析,可证明本文方法能够很好地识别同类铜币以及区分不同类型铜币。

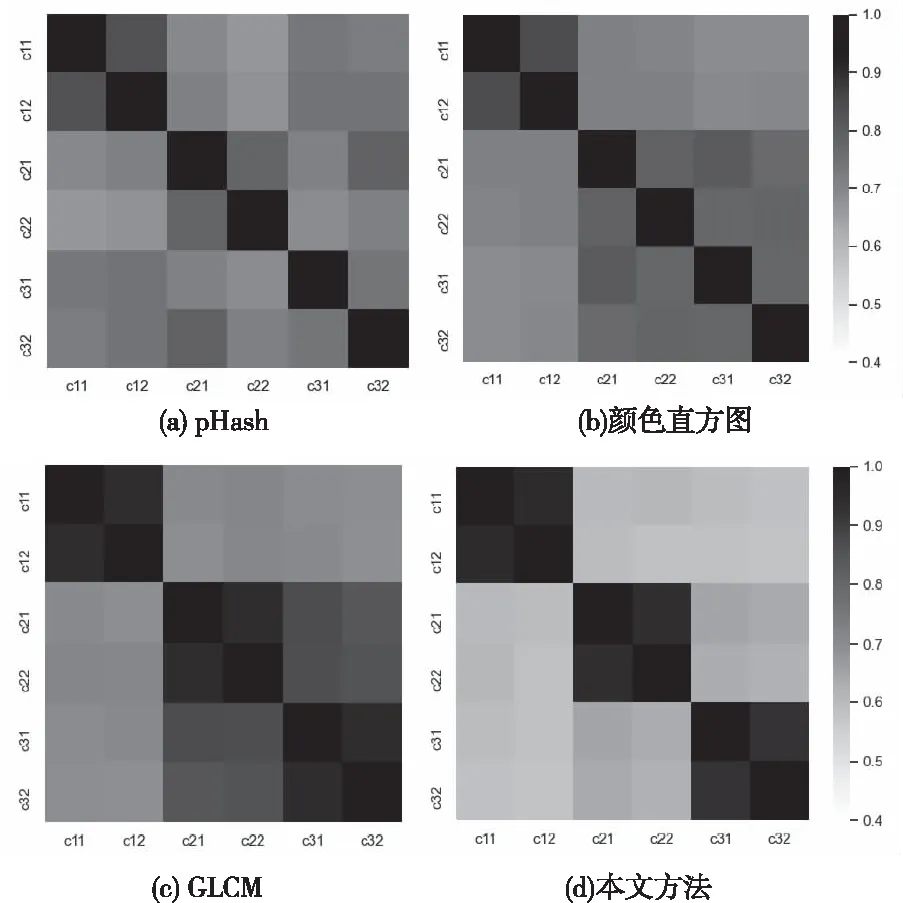
图8 几种图像相似度计算方法结果比较

5 结论

针对同类铜币表面复杂而人工观察无法进行定量化评判这一问题,本文提出通过计算机视觉图像相似度比较方法实现定量地识别同类铜币。方法对铜币提取出的128维SURF特征具有较强的独特性和可区分性,对旋转、光照和尺度变化均具有高度鲁棒性。实验表明本文基于128维SURF特征的相似度计算方法能够很好地识别与区分不同状况的铜币:对于同类铜币,其相似度得分均高于0.9;而不同铜币之间的相似度为0.65以下,远低于同类铜币。

本文就利用计算机视觉识别铜币提供一种思路,未来将尝试结合深度学习算法进一步提升识别准确率。