基于MDS-WFCM的日负荷曲线聚类方法
2023-06-01杨俊杰
杨 邓,杨俊杰,2
(1. 上海电力大学电子与信息工程学院,上海 200090;2. 上海电机学院,上海 201306)
1 引言
近年来,随着智能电网数字化、信息化的不断发展,电网公司积累了海量的用电负荷数据。聚类算法就是通过挖掘用户的用电行为实现对电力用户负荷曲线有效分类,对电网的实时调度以及运行规划等方面提供一定的参考意义。常用的聚类方法有直接聚类和间接聚类。程江州等[1]采用CK-means算法对负荷曲线直接聚类,但直接聚类方法在计算效率、聚类质量等方面存在着严重的不足。间接聚类是将原始负荷数据进行降维或特征提取,然后进行二次处理的技术。陈菲等[2]采用多层凝聚方法降低负荷曲线的维度,提高了聚类精度。陈烨等[3]采用SVD分解将高维负荷数据映射至低维坐标中,实现降维聚类。宋英军等[4]将欧式距离与动态时间弯曲距离相结合提取出日负荷曲线的整体与局部等3种特征,采用K-means算法对日负荷曲线聚类。
上述研究成果,采用的降维方式不能准确反映原始负荷曲线的特征,这会对聚类的效果产生影响,从而影响聚类的质量。鉴于此,本文提出了一种基于多维标尺及加权模糊C均值聚类的日负荷曲线聚类方法。通过MDS降维技术保留了原始负荷曲线之间的特征,结合加权模糊C均值聚类方法达到对负荷曲线的精准分类。以我国某地区真实数据为例,验证了本文方法的有效性。
2 MDS降维理论
将MDS理论[5,6]应用于日负荷曲线降维中,假定一个由m条负荷曲线,每条负荷曲线有n个采样点,其构成原始空间的距离矩阵D∈Rm×m,表示为

(1)
dij表示第i个用户负荷曲线到第j个用户负荷曲线之间的欧氏距离,将原始n维空间数据降至q维空间表示为Z=[z1,z2,…,zm]∈Rm×q,第i个用户的负荷数据为zi=[zi1,zi2,…,ziq],且满足任意两个用户在q维空间中的欧氏距离等于n维空间的欧氏距离,以此达到降维效果。
根据降维前后距离不变原则可得
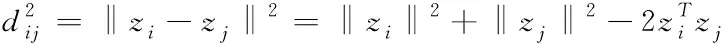
(2)
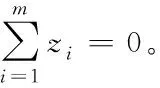
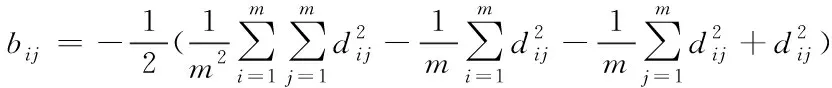
(3)
对矩阵B做特征值分解,得:B=VΛVT,其中Λ=diag(λ1,λ2,…,λn)为矩阵B的特征值构成的对角矩阵,满足λ1≥λ2≥…≥λn,V为特征向量矩阵。取前q个最大非零特征值,它们构成的对角矩阵为Λq=diag(λ1,λ2,…,λq),对角阵元素依然按照降序排列令Vq为其对应的特征向量矩阵,则降维后矩阵Z可以表示为
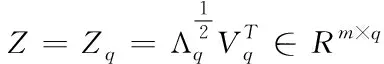
(4)
3 基于MDS-WFCM的聚类算法
3.1 数据预处理
3.1.1 异常数据处理
负荷数据在采集过程中由于仪表故障、传输通信故障等常常会产生异常数据。当采集的某条负荷曲线的异常量高于10%及以上时,就认为该条负荷曲线无效,反之,则通过式(5)进行修正。本文假设某条负荷曲线xk=[xk,1,xk,2,…,xk,n]经检测存在异常且异常量低于10%,则其修正量为
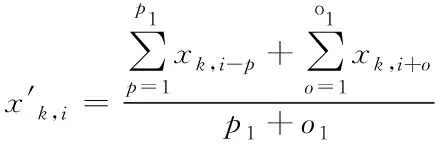
(5)
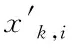
3.1.2 负荷数据归一化
为防止原始数据之间因数量级差异影响聚类效果。需要将原始数据归一化处理变换至[0,1]之间。本文采用最大值归一化的方法,如式(6)所示

(6)
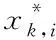
3.1.3 高斯平滑处理
在实际的负荷数据采集过程中,所采集的数据不可避免的会受到多种干扰信号或者设备故障等因素导致负荷数据存在较大的波动。采用高斯平滑处理能够消除因为数据突变而带来的高额噪声干扰,起到更好的聚类效果。以某条负荷曲线为例,平滑处理前后的负荷曲线对比如图1所示。

图1 负荷曲线的平滑处理
3.2 确定降维指标及权重
为了充分利用第2节中矩阵B特征值的下降趋势,本文采用最小二乘法来确定q值的大小,步骤如下:
Step 1:计算特征值。对矩阵X多维标尺处理,获得n个特征点(i,λi)组成的数据集S。
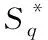
Step 3:求拟合误差。求出前q个特征点的拟合平均误差Tq,并计入数据集T。
Step 4:计算q=q+1,重复Step2和3,当q>n时,转到Step 5。
Step 5:确定降维指标q的值。找出数据集T中的最小值,对应的q值即为最终的降维指标数目。
改进熵权法配置指标权重如下
1)计算熵值ej。第j个降维指标的熵值可由下式确定
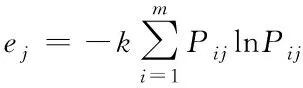
(7)
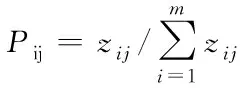
(8)
式中:i=1,2,…,m,j=1,2,…,q;k为常数,k=1/lnm;Pij为第i个用户下的第j个被评价对象的贡献度。
2)计算权重wj。利用改进后的权重计算公式计算wj
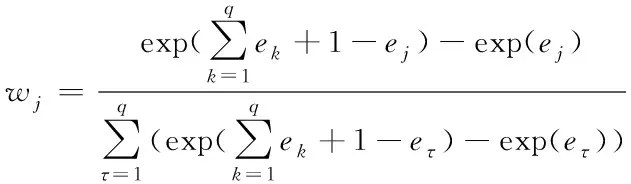
(9)
式中:wj∈[0,1],且满足
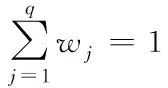
(10)
3.3 WFCM聚类算法
考虑指标权重对聚类结果的影响,本文采用的WFCM算法与传统FCM算法稍有不同,步骤如下:
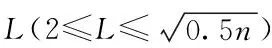
Step 2:确定隶属度矩阵U。隶属度矩阵U=[U1,…,Ui,…,Um],Ui=[ui1,…,uij,…,uiL],其中uij表示zi属于第j个聚类中心的隶属值,uij可以表示为
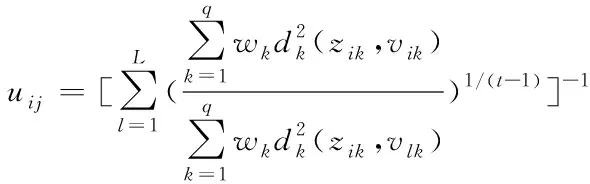
(11)
Step 3:计算目标函数J。在负荷曲线聚类过程中,将每个用户负荷数据到所有聚类中心的距离的加权平方和定义为目标函数:
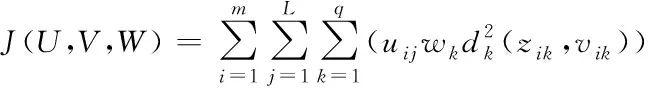
(12)
Step 4:更新聚类中心。若Step 3中目标函数J的值未达到最小,那么需要根据式(13)重新选取聚类中心并返回Step 2。
(13)
Step 5:当目标函数J达到最小值时,算法结束。
采用的加权模糊C均值算法是在原始FCM的基础上对隶属度矩阵、目标函数等更加细致化的调整,对聚类效果有更进一步的提升。
3.4 聚类有效性检验
聚类的有效性检验是通过聚类有效性指标确定最佳的聚类数。常用的指标有XB指标、SC指标、SSE指标、CHI指标、DBI指标等[7]。其中XB指标在模糊聚类当中是较为有效的指标。XB指标值越小,代表的聚类效果越好,并且该指标相对于其它指标更加适合用于负荷曲线聚类的研究。由于本文考虑计入权重的影响,故XB指标计算公式如下
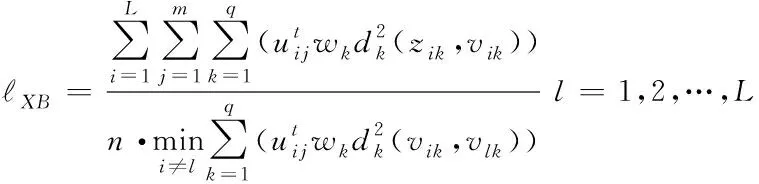
(14)
XB指标的分子与分母分别反映的是类内紧凑程度与类间分散程度,当类内紧凑度越小,类间分散度越大时,即XB值越小,聚类效果越好。反之,不然。所以当XB指标取得最小值时所对应的L即为最佳聚类数。
本文的MDS-WFCM负荷聚类算法流程图如图2所示。
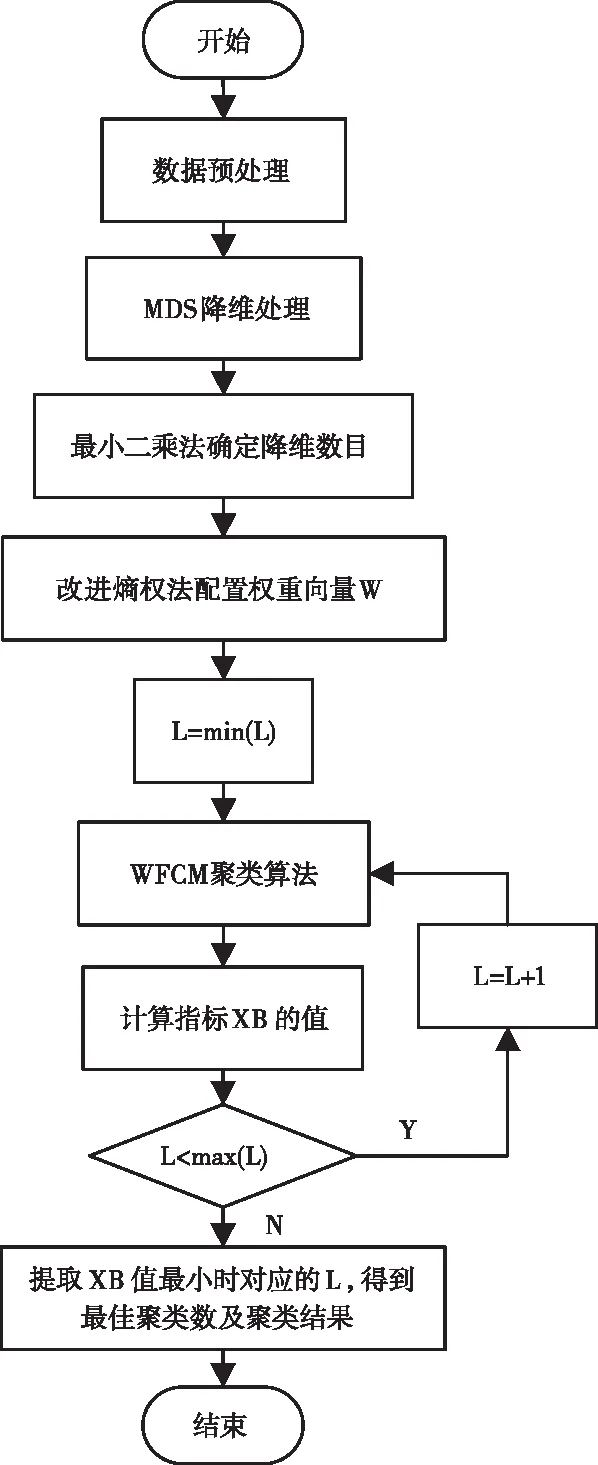
图2 基于XB指标的MDS-WFCM负荷聚类算法流程图
4 算例仿真分析
4.1 实际日负荷曲线聚类分析
本算例选取中国北方某地区2017年9月某个工作日2142个用户的日负荷曲线为研究对象,采样间隔为30min,每条负荷曲线共计48个采样点。样本数据经预处理去除无效负荷曲线后,最终共含2112条有效的日负荷曲线,构成2112×48阶初始矩阵。
采用MDS降维后绘制矩阵B的特征值曲线,如图3所示。采用最小二乘法,求平均拟合误差Tq,拟合误差集如表1所示。

表1 拟合误差集
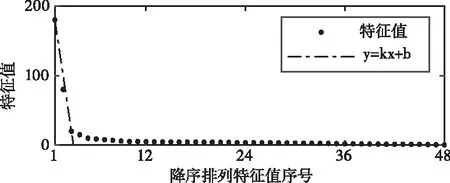
图3 特征值曲线
由表1可知,当q为3时,Tq取最小值,获得最佳拟合曲线y=kx+b,如图4所示。因此本算例最佳降维数为3,初始2312×48阶矩阵便转换为2312×3阶降维矩阵Z,同时采用改进熵权法获得3个降维指标对应的权重向量为W=[0.65,0.27,0.08]。以矩阵Z以及权重向量W作为输入,采用加权FCM算法进行聚类,将聚类结果与负荷数据经预处理后直接利用FCM算法聚类(以下称为传统方法)对比。
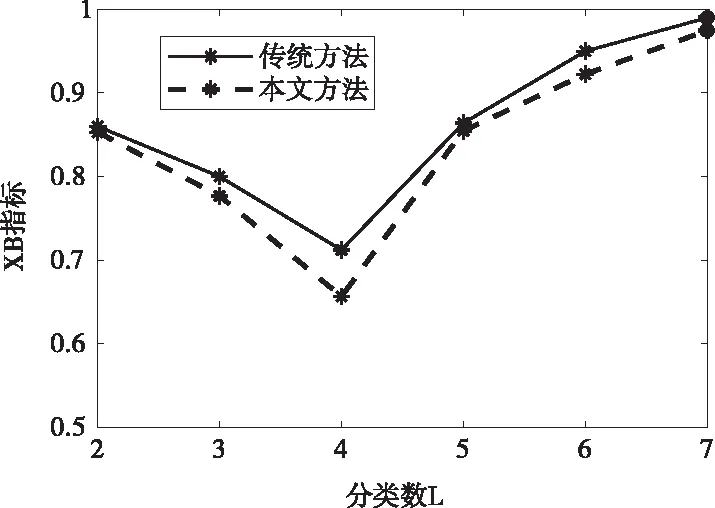
图4 两种方法在不同聚类数下的XB指标
由图5本文方法与传统方法在不同聚类数下的有效性检验指标可知,两种方法分类数对应XB指标走势基本相似,当聚类数为4时,两种方法的XB指标值均取得最小值,因此两种方法确定最终的聚类数均为4。
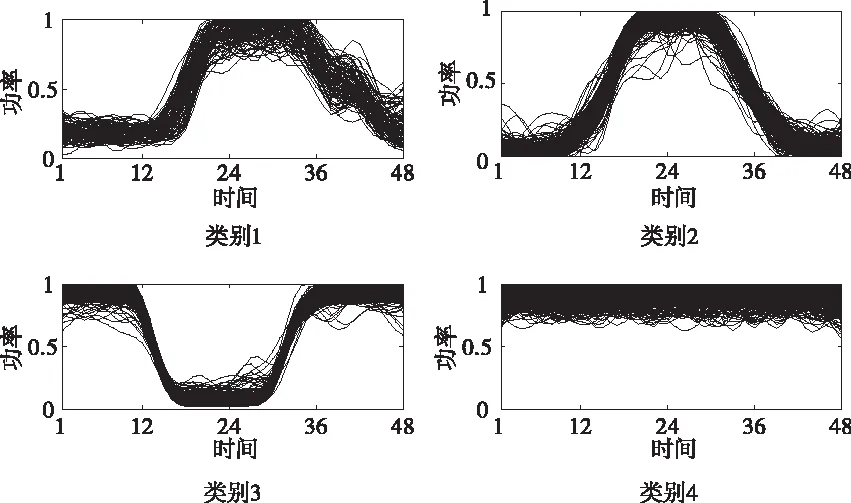
图5 本文方法聚类结果
如图6、7所示,本文方法聚类结果中4类曲线数目分别为544、547、362、659,传统方法聚类结果中对应的4类曲线数目为563、528、362、659。从分类结果可以看出传统方法在类别1与类别2之间存在少量的误分。分析其原因,传统方法是以负荷数据之间的距离作为相似性判据进行的聚类,这会因为样本数据维度较高导致聚类质量效果较差。而本文方法所采用的MDS降维特征提取,在保证负荷曲线之间距离不变的情况下,以负荷主要特征作为聚类的依据,分类结果相对准确且稳定,在聚类质量上优于传统方法。虽然两种方法在结果上存在一定的差异,但总体分类结果仍具有高度的相似性。

图6 传统方法聚类结果
图7为两种方法提取的聚类中心曲线。具体分析这四类曲线:第1类负荷曲线为双峰型,主要用户包含政府、公共事业单位等用电较为规律。第2类负荷曲线为单峰型,主要为某些商场、写字楼等。第3类负荷曲线为避峰型,主要包括夜间用电量高的行业,如公用路灯、网吧、KTV、酒吧等。第4类负荷曲线为平峰型,主要包括大工业,制造业等用电量持续高峰。分析表明,本文方法和传统方法聚类中心曲线较为相似,但从工程角度分析,本文方法更能体现用户的实际用电特征,具有较好的应用价值。
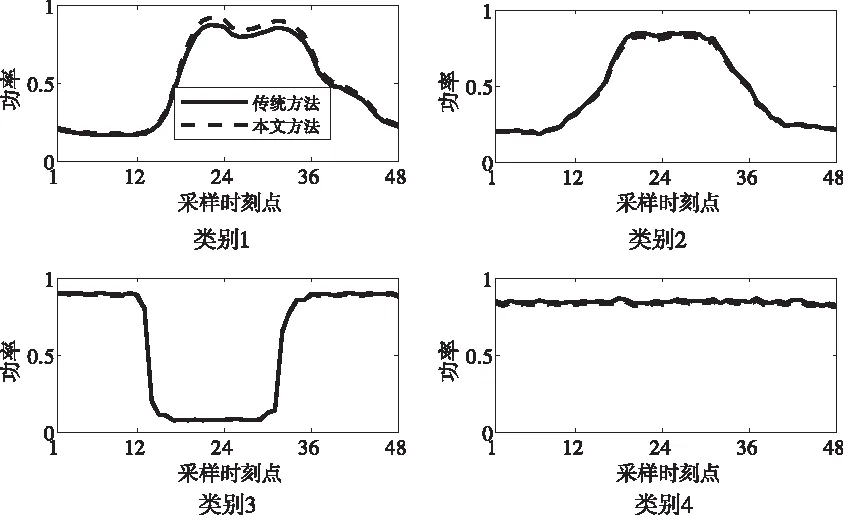
图7 两种方法聚类中心曲线对比
综合比较两种方法的性能,如表2所示,在同时取得最佳聚类数目的情况下,使用本文方法的总的程序运行时间仅为4.83s,相对于传统方法缩短了64.8%,且XB指标值以及聚类过程迭代次数也均小于传统方法。不难发现,本文方法在运行效率和聚类质量上具有较大的优势,体现了本文方法的有效性。
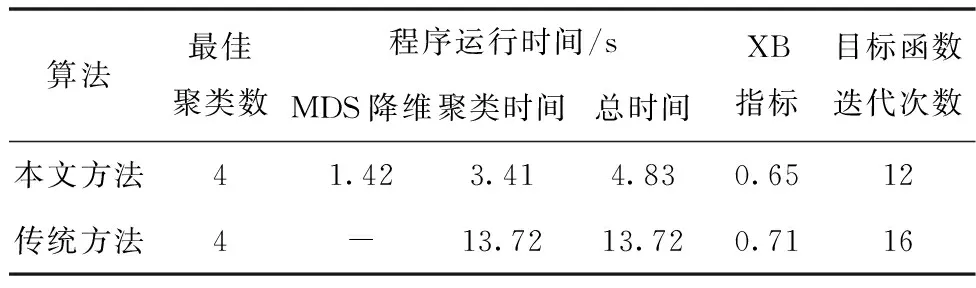
表2 两种方法聚类结果性能对比
4.2 算法鲁棒性检验
为了检验本文所提聚类方法的鲁棒性[8],这里基于6类典型日负荷曲线,并在每类负荷曲线每个数据点加入一定比例r的随机噪声。模拟出每类200条,共计1200条日负荷曲线。当噪声比例r为20%时,6类典型曲线如图8所示。
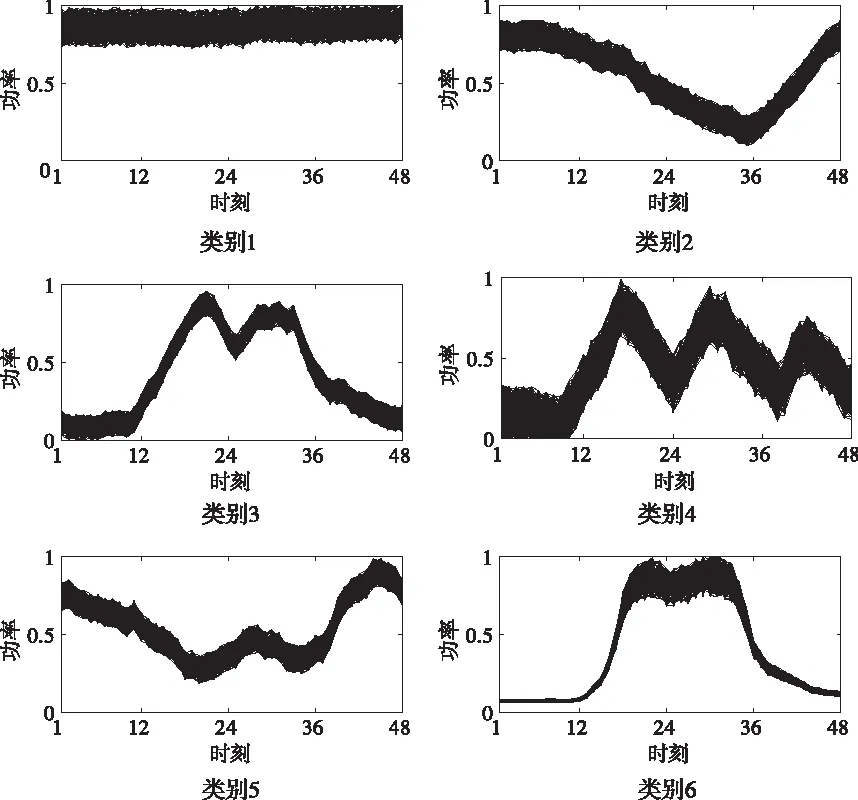
图8 1200条模拟曲线(r=20%)
改变噪声比例r的大小,然后采用本文和传统两种方法对模拟的负荷曲线聚类分析。这里定义聚类准确率h为分类准确的负荷数量占总负荷数量的百分比。以最佳聚类数、XB指标、聚类准确率h来对比本文和传统两种算法的鲁棒性,结果如表3所示。
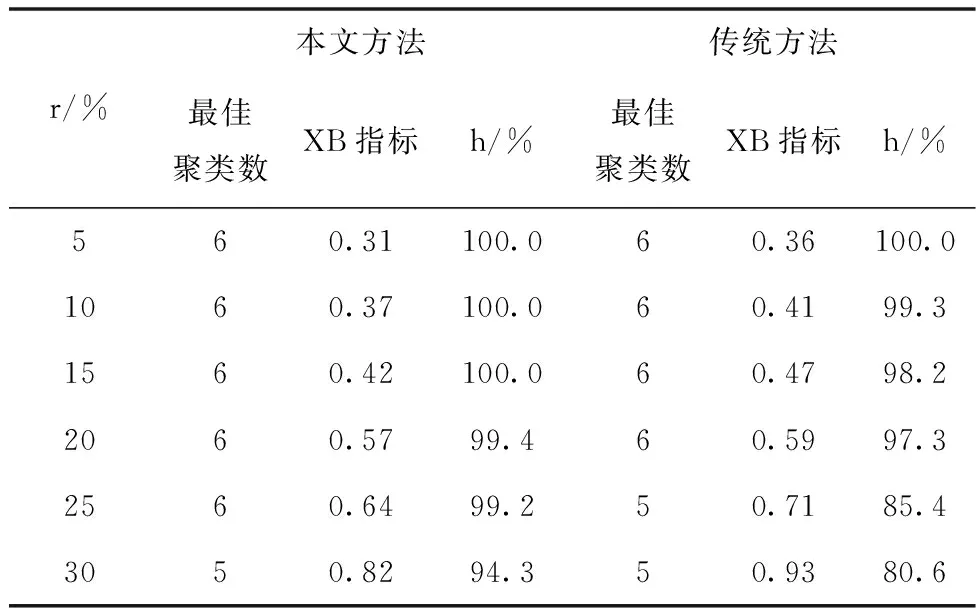
表3 不同占比扰动信号下两种方法鲁棒性对比
根据表3可以得出以下结论。
1)随着噪声比例的依次递增,两种方法XB指标值也越来越大,分类准确率h开始出现下降趋势,同时最佳聚类数也随着噪声比例的增加出现一定的偏差。因此可以用该3种指标衡量算法的鲁棒性。
2)当所加噪声比例较小时,两种方法的分类准确率均接近于100%。但随着噪声比例的增加,对于本文方法,当扰动比例达到30%时,最佳聚类数开始出现偏差,分类准确率也出现一定的下滑。对于传统方法当扰动比例达到25%时,最佳聚类数不再为6,同时分类准确率也出现了大幅度下滑。
通过对比,不难发现,本文方法抗干扰能力优于传统方法,鲁棒性较好。在一定强度的干扰下能够较为准确的反映日负荷曲线的主要特征。
5 结论
本文提出了一种基于MDS-WFCM的日负荷曲线聚类方法,通过MDS降维技术对原始负荷曲线进行降维,采用最小二乘法确定降维数目以及改进熵权法配置权重,最后采用加权模糊C均值聚类算法进行聚类。通过本文算例可以得出以下结论:
1)该方法用于负荷曲线聚类在总体效率、聚类质量、鲁棒性等方面具有一定的优越性,均优于传统方法,具有一定的参考价值。
2)采用MDS降维方法,使降维后用户负荷曲线之间的距离维持了原有高维空间的相应距离,从而使降维后的负荷曲线能够保持原有的重要特性,是对聚类质量的潜在提升。
3)本文采用改进熵权法来配置3个指标权重,避免了传统熵权法计算带来的误差,在一定程度上保证了聚类结果的客观性与准确性。选用加权模糊聚类算法,在聚类过程中自适应配置各项指标的权重,对聚类的准确度有了更进一步的提升。
本文提出基于多维标尺降维聚类算法,有助于掌握用户的用电特征,对用户用电异常检测、电网需求侧响应等方面具有实际的参考意义,如何将该方法在实际中应用也是本文下一步研究的重点。此外,是否有其它优化算法对于本文降维方法的改进也是本文下一阶段研究的内容之一。
