基于役龄回退模型的露天矿卡车周期预防性维护策略

李雯静 ，邱 莉 ，林志勇 ，姚 囝 ，谢展扬

（1.武汉科技大学 资源与环境工程学院, 湖北 武汉 430081；2.武汉大学 遥感信息工程学院, 湖北 武汉 430079）

0 引 言

在过去几十年，露天采矿通过引进超大型机械和高度自动化的设备不断实现现代化。卡车运输是露天采矿业中最传统、最经典的运输方式，与所有类型的机械类似，露天矿卡车也需要根据维护计划进行仔细维护，但其维护成本有时占露天矿运输成本的30%～50%[1]。预防维护措施可以延长露天矿卡车的寿命降低故障率，并有利于减少露天矿卡车在运输中的能源消耗和温室气体排放[2]。研究露天矿卡车预防维护策略对于实现可持续和经济的露天矿生产起着关键作用。

许多研究人员对矿用设备的维护问题做了研究，胡明振等[3]根据矿用电动轮汽车维修成本数据，建立电动轮的日常维修成本数学模型与实际大修周期数学模型，以此确定电动轮汽车维修周期；王广慧等[4]通过引入故障率和等效役龄建立了矿用变压器的检修策略优化模型，并利用布谷鸟搜索算法求解了该模型；张旭辉等[5]结合数字孪生技术设计了的矿用设备维修指导系统，提高了矿用设备的故障维修指导效率。徐畅等[6]在矿用设备出现故障前实现智能报警，及时提供相应的设备预知维护方案；于嘉成等[7]采用松耦合方式集成矿山设备的生命周期数据，基于状态设备监测数据判别算法预判设备是否需要检修；刘威等[8]采用MCMC 算法预测露天矿典型设备的故障类别和发生时间，揭示了设备故障发生规律。针对卡车维护方面的研究，OZDEMIR B等[9]分析了操作员对卡车可靠性的影响，并证明操作员得到好的培训是延长卡车寿命的有效手段；OZDEMIR B 等[10]通过收集露天矿卡车历史可靠性数据计算其虚拟年龄，依据该信息安排设备的维护计划；PERALTA S 等[11]收集露天矿卡车的历史故障数据建立其可靠性模型，通过给定4 个不同维修周期时间研究证明最短的维修周期在可靠性方面效果最好，但代价是维修频率最高及维修成本最高；刘设[12]根据设备的t时刻和历史的性能特征参数预测设备运行性能状态，根据设备实际情况调整维修计划。ANGELES E 等[13]首先通过收集露天矿卡车的历史故障数据建立其可靠性模型，然后根据所需的可靠性水平确定最佳检查间隔，最后考虑每次维修后设备的虚拟寿命制定预防性维修计划。另外许多作者在露天矿卡车调度研究中考虑卡车维护成本的不确定[14-16]。

以上研究对矿山设备管理具有一定的指导意义，但很少考虑露天矿卡车预防维护后故障率的变化规律，也未对卡车不同运行时间的预防维护策略进行研究。针对此问题，笔者引入役龄回退因子构造每次预防维护后的故障率函数，从矿山企业设备管理角度出发，建立露天矿卡车预防维护总成本模型，设计了求解算法。最后，针对露天矿卡车不同运行时间进行了实验，研究了最优维护次数随卡车运行时间的变化规律。

1 基于役龄回退模型构建露天矿卡车故障率函数

设备维护主要有事后维修和预防维护两类。定周期预防维护因其有利于生产计划的制订和执行是目前运用较多的预防维护方式[17]。事后维修最常用的是小修，它不改变露天矿卡车的故障率。对露天矿卡车执行预防性维护，使卡车介于“恢复如新”和“恢复如旧”之间，它改变卡车的故障率。为了便于矿山企业对卡车进行管理，采用周期预防维护和故障发生后小修相结合的方式对卡车进行维护。

设备故障是维护的前提，分析设备故障特征，可以为管理层提供针对性的维护决策[18]。常用的故障函数有威布尔分布、正态分布和指数分布[19]。威布尔分布是故障率函数的一种重要形式，可分为早期失效期、偶然失效期和损耗失效期3 个阶段，它适用于机械电气设备累计失效产品的故障分布模拟[20]。露天矿生产运输所需的卡车是一种机械设备，由于其在露天矿生产中的使用负荷、磨损磨耗、自然侵蚀等因素的影响，其役龄和故障率会不断增加。文献[11]和[13]通过收集并分析露天矿卡车历史故障数据，证明了露天矿卡车的故障率函数服从威布尔分布且处于损耗型失效阶段。根据威布尔分布，露天矿卡车故障率函数可表示为

其中，h(t)、η 、β分别为故障率函数、尺度参数和形状参数；t为露天矿卡车运行时间。其中，当0<β<1时 ，故障率随时间单调递减；当 β=1时，故障率为常数；当 β>1时，故障率随时间单调递增，呈现出损耗型失效的特点，此时进行预防维护才有意义。

针对露天矿卡车每次预防维护前后故障率会产生变化的特点，引入役龄回退因子α 来反映露天矿卡车在每次周期预防维护后的故障率变化，为后续更准确地评估露天矿卡车故障率变化规律奠定基础。在对露天矿卡车执行预防维护周期为T的周期预防维护时，其故障率会回退到周期预防维护前(1-α)T时刻，露天矿卡车役龄回退量为 αT，此时露天矿卡车实际役龄Ts表达为

对露天矿卡车执行周期预防维护策略，其故障率变化规律呈递推模式，变化规律如下：

其中，h0(t)为未进行预防性维护的故障率函数；h1(t)为进行第一次预防性维护后的故障率函数；hi(t)为进行第i次预防性维护后的效率函数；T为待优化的预防维护周期；N为待优化的周期预防维护次数。

由此，可得卡车在进行第i次预防维护后故障率函数hi(t)为

2 露天矿卡车周期预防维护成本模型及求解算法

结合第1 节基于役龄回退模型构造的露天矿卡车每次维护后的故障率函数，构造露天矿卡车周期预防维护成本模型，设计该模型的求解算法，求取露天矿卡车最优的周期预防维护维护策略。

2.1 预防维护总成本

对露天矿卡车进行预防维护的目的是保证其在露天矿生产运行中安全可靠。建立露天矿卡车周期预防维护成本模型是为了寻求既能保证露天矿卡车安全可靠运行又具有经济性的最优维护方案。合理执行露天矿卡车的预防维护周期T，从而使得在卡车运行时间L内的预防维护总成本的值最小，是矿山企业管理者关心的问题。

露天矿卡车的预防维护总成本由周期预防维护成本和发生故障后的小修成本组成，用C(T)表示，是关于T待优化的目标函数，如式（1）：

其中，C1为 每次对卡车执行定周期预防维护费用；C2为卡车运行中每次发生故障采用小修的费用。由露天矿卡车执行第i次预防维护后故障率函数hi(t)可得其在进行第i次预防维修后故障次数Mi和运行时间L内故障总次数M分别为

2.2 最优周期预防维护策略

为了获得露天矿卡车在运行时间L内的最优预防维护总成本C(T)、最优预防维护次数N*和最优预防维护周期T*，需求解露天矿卡车预防维护总成本以获取最优周期预防维护维护策略。

当N给定时，可以得到T取值范围为[L/N(N+1),L/N]，露天矿卡车预防维护总成本C(T)关于T的一阶导数C′(T)为

由文献[11]和[13]证明了露天矿卡车的故障率函数符合威布尔分布且处于损耗型失效阶段可知β>1，役龄回退因子0 ≤α ≤1，则C′(T)>0，即露天矿卡车预防维护总成本C(T)是关于预防维护周期T的增函数。因此，当N给定时，预防维护总成本C(T)的最小值在T=L/(N+1)处取得。

基于此给出具体的算法步骤。

Step1：令N=1。

Step2：令i=0，计算露天矿卡车第i次预防维修后故障次数Mi。

Step3：i=i+1。若i≤N，则执行第2 步；否则，执行第4 步。

Step4：计算露天矿卡车运行时间L内发生故障的次数M与Tmin=L/(N+1)，并计算C*(Tmin)。

Step5：N=N+1。若N≤N¯ （其中N¯可以取任意大的整数，本文取100），则执行第2 步；否则，执行第6 步。

Step6：搜索当在1 ≤N≤N¯ 范围取值时，C*(Tmin)的最小值，即为预防维护总成本的最优值C*(T)。

基于上述算法，可获得露天矿卡车运行时间L内的最优预防维护周期T*和 最优预防维护次数N*。

3 露天矿卡车算例分析

3.1 模型参数

参考文献[11]根据露天矿卡车历史故障数据，利用最大似然估计法分析其故障率函数服从参数η、β分别为660.94、1.49 的威布尔分布。最大似然估计法求解威布尔参数η、β过程如下：

由威布尔分布可得露天矿卡车概率密度函数为

则似然函数为

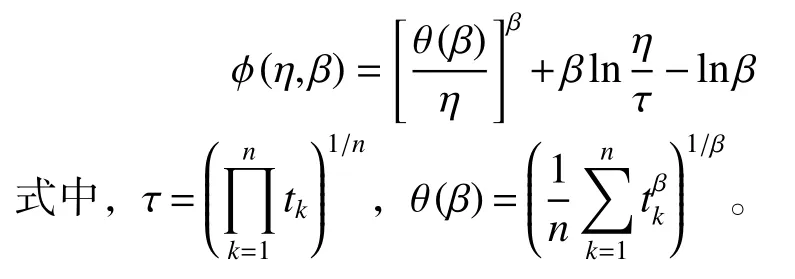
根据最大似然估计法，先对似然函数分别关于η、β求偏导，然后进行代数变换可得：

役龄回退因子α 参考文献[21]取0.95，本文基于此研究露天矿卡车最优周期预防性维护策略。

3.2 试 验

基于3.1 节模型参数进行试验，当露天矿卡车运行时间L固定时，求取最优预防维护策略；然后探究露天矿卡车预防维护总成本最优值C*(T)、最优预防维护周期T*和 最优预防维护次数N*随露天矿卡车运行时间的变化；最后做了露天矿卡车最优周期预防维护策略与计划性检修策略的成本对比试验。

假定露天矿卡车周期预防维护的成本C1为500 元，小修成本C2为300 元，露天矿卡车运行时间L为40 000 h，根据2.2 算法可得总成本最优值C*(T)为5.42 万元，对应最优预防维护周期T*和最优预防维护次数N*分别为1 904.76 h、20 次。为了探究卡车运行时间L为40 000 h 时维护次数N、维护周期Tmin与维护成本C*(Tmin)三者的关系，绘制其三维图如图1 所示。由图1 可知，当L确定时，C*(Tmin)的值随着N的增加先减小后增大，C*(Tmin)的值随着Tmin的变长先变小再变大。

图1 维护次数、维护周期与维护成本关系Fig.1 Three-dimensional relationship of maintenance cost,maintenance frequency and maintenance cycle

为便于矿山设备管理针对不同情况做出最合适露天矿卡车的维护计划，计算卡车运行时间L从5 000～100 000 h 的预防维护总成本最优值C*(T)、最优维护周期T*和 最优维护次数N*，计算结果见表1。为探究最优预防维护次数N*随露天矿卡车运行时间的变化，根据表1 绘制最佳预防维护次数N*时间序列图，如图2 所示。由图2 可知，随着露天矿卡车运行时间的变长，最优预防维护次数N*呈现增长趋势。

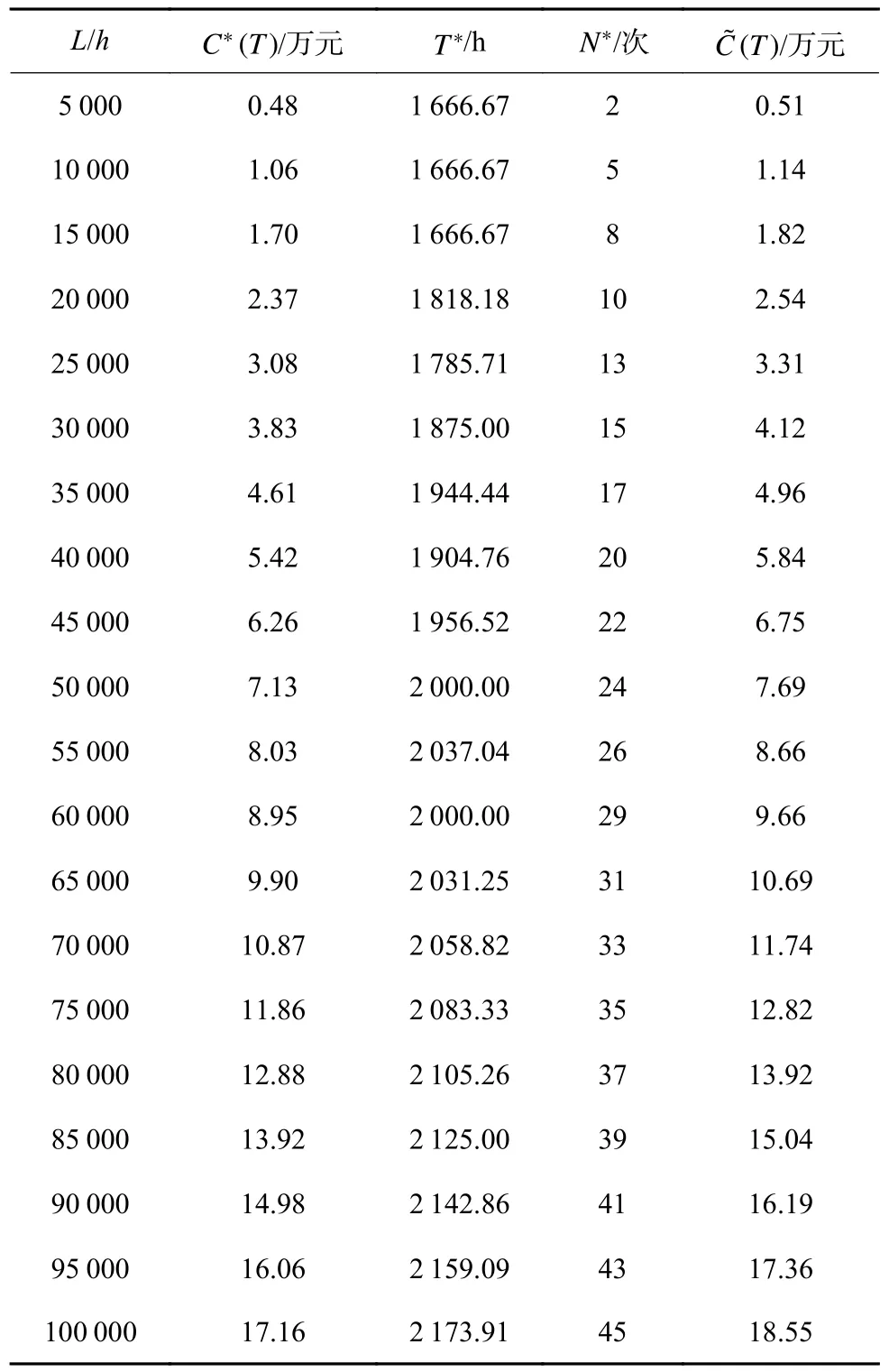
表1 运行时间不同时对应的最优周期预防维护策略Table 1 Optimal periodic preventive maintenance strategy corresponding to different operating time

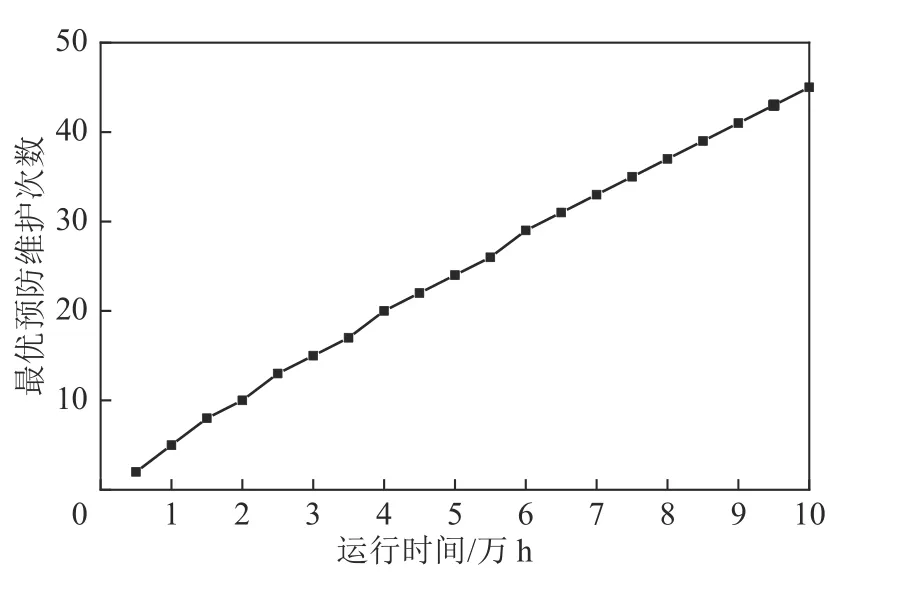
图2 最优预防维护次数随运行时间变化示意Fig.2 Schematic of best preventive maintenance times with operating time

目前露天矿卡车多采用每运行1 000 h 进行一次计划性检修策略，根据式（1）计算此策略下卡车运行 时 间L从5 000～100 000 h 的 总 成 本C˜(T)，见表1。并绘制当露天矿卡车运行时间L不同时，其与本文周期预防维护策略最优成本对比图，如图3 所示。由图3 可知，与本文周期预防维护策略最优成本相比，采用每运行1 000 h 进行一次计划性检修策略所需成本更多，且随着露天矿卡车运行时间的增长差值越来越大，说明对露天矿卡车进行预防维护优化可以节约成本，研究露天矿卡车预防维护策略优化有利于露天矿可持续和经济发展。

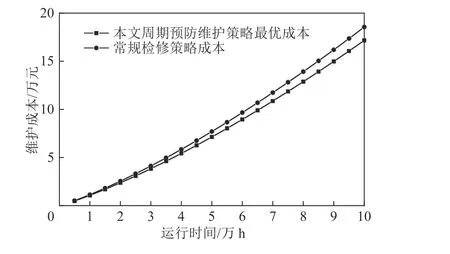
图3 成本对比Fig.3 Cost comparison

4 结 论

1）从露天矿卡车故障率的角度研究露天矿卡车周期预防维护策略，首先引入役龄回退因子构造露天矿卡车每次周期预防维护后的故障率函数，然后建立包括露天矿卡车小修成本和周期预防维护成本的预防维护总成本模型，最后设计了求解该模型的算法。

2）试验中当露天矿卡车运行时间为40 000 h 时，对应的最优预防维护总成本、最优预防维护周期、最优预防维护次数分别为5.42 万元、1 904.76 h、20 次，分析三者关系可知预防维护成本随着预防维护次数增加先减小后增大，随着预防维护周期变长先变小再变大。

3）计算露天矿卡车运行时间从5 000～100 000 h的最优周期预防维护策略，通过分析最优维护次数随露天矿卡车运行时长变化关系可知，随着露天矿卡车运行时间的增长，最优预防维护次数呈现增长趋势。

4）通过成本对比，露天矿采取最优周期预防维护策略比常用的维修策略的所需成本更少且随着露天矿卡车运行时间的变长差值变大，说明对露天矿采取最优周期预防维护策略更利于露天矿可持续性生产。