基于改进随机森林算法的地质构造识别模型
2023-06-01王怀秀冯思怡刘最亮
王怀秀 ,冯思怡 ,刘最亮
(1.北京建筑大学 电气与信息工程学院, 北京 102616;2.华阳新材料科技集团有限公司, 山西 阳泉 045000)
0 引 言
随着煤炭资源向深部开采,煤层开采难度增大,各种复杂的地质构造严重影响煤矿开采人员安全。地震属性就是经过数学变换而导出的有关地震波的几何形态、运动学特征、动力学特征和统计学特征,通过对地震属性进行分析,并做出标定,消除畸变,就有可能揭示有关储层信息。然而地下地质情况的复杂性和地震信息的影响因素太多,存在较大的不确定性或模糊性,应用任何单一的地震属性都不能准确地进行构造识别,展开地震多属性融合分析就显得十分必要。
地震属性融合的研究有很多种,BALCH[1]于1971 年将地震资料用彩色进行显示,提高了对地下地质异常的识别能力。2002 年,我国乐友喜教授[2]优先将聚类分析的方法应用于地震属性融合,多元线性回归法[3]也可以用于属性融合(季玉新和欧钦,2003)。随着大数据时代的来临,目前发展较快的是基于地震属性数据的融合,即通过数学统计、人工智能等方式提取最优地震属性,如2010 年,曹琳昱[4]首次将基于粒子群优化的 BP 网络技术应用于多属性融合中。神经网络融合属性法识别速度很快,并且自适应性以及容错能力强,该方法适用范围广。但这种方法不能自主优选属性,同时需要足够的样本数据来对网格进行训练;2012 年,Bruno 将 PCA[5]用于断层属性的融合,通过对地震属性进行 PCA 融合,得到了融合后的新属性,对于微小断层识别的准确度有了较大的提高。但是PCA 是一种线性降维方法,当数据中存在非线性关系的时候,PCA 的效果会大打折扣;2017 年,孙振宇[6]将SVM 算法用于地震小断层识别,SVM 模型融合各属性预测断层的优势,从不同的角度挖掘断层信息,降低了解释人员主观因素对解释结果的影响。但是在构建SVM 模型时,模型本身的结构直接影响模型识别准确率,且地震属性的选择对模型准确率影响也很大。
近年来,地震属性融合技术发展迅速,已广泛应用于储层预测[7-8]、砂体预测[9-10]、构造识别等各个领域。在地震属性融合过程中,需要解决的关键问题是选择一种准确率高并且适用于多种样本数据集的算法,能够更有效地对地震属性数据进行解释,提高构造识别模型的准确率。
随机森林算法作为一种高度灵活的算法近年来广受欢迎,拥有广泛的应用前景。在当前所有的算法中,作为一种集成算法的随机森林算法本身精度比大多数单个算法好,准确性高,且对数据集的要求不高,适用于多种数据集(线性与非线性、高维数据集等)。随机森林算法的随机性在于2 个方面:①每棵树的训练样本是随机的,②树中每个节点的分裂属性集合也是随机选择确定的。正因为这两个随机性,随机森林对噪声数据不敏感,克服了过拟合的问题。但是目前为止,对随机森林中决策树的数量k、单棵决策树的最大特征数m等参数进行优化与选择的研究还比较少,一般情况下都是通过经验选择参数,往往可能不是最优参数。
针对上述问题,提出一种改进的网格搜索算法,基于模型得分对算法模型进行评估,对随机森林算法的分类器数量与单棵决策树的最大特征数这2 个参数进行优化,克服以往依据经验选择参数的缺点,选取最优参数值,并且利用得到的算法模型进行地质构造识别与预测。
1 随机森林算法及优化
1.1 随机森林算法原理
2001 年,Breiman 等提出随机森林算法[11](Random Forest,简称RF)。该算法是一种基于传统的决策树理论的集成学习(Ensemble Learning)方法。随机森林在决策树的训练中引入随机属性选择。具体来说,传统决策树在选择划分属性时是在当前结点的属性集合(假定有d个属性)中选择一个最优属性;而在随机森林中,对基决策树的每个结点,先从该结点的属性集合中随机选择一个包含d个属性的子集,然后再从这个子集中选择一个最优属性用于划分。随机森林通过Bagging(集成)方法,生成彼此之间互不相同的训练样本集,该算法主要用于分类和回归,对于分类问题,采用简单多数投票法的结果作为随机森林的输出;对于回归问题,根据单棵树输出结果的简单平均作为随机森林的输出[12]。文中,我们选择随机森林分类算法进行分类预测。
随机森林的算法流程如图1 所示[13]。
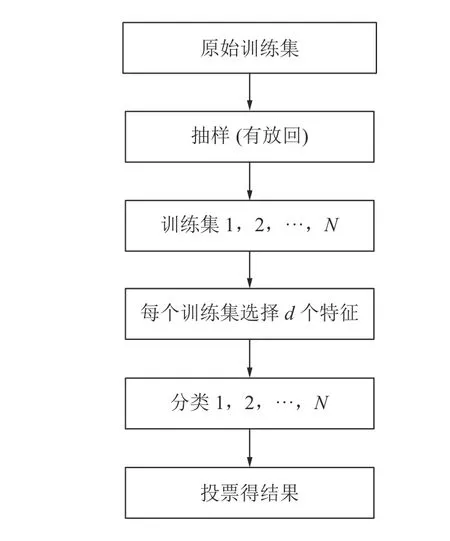
图1 随机森林算法流程Fig.1 Random forest algorithm flow
1)假设原始训练集有N个样本,应用bootstrap 法随机有放回的抽样组成训练集;
2)设样本有D个特征,在每一棵树的每个节点处随机抽取d(d<D)个特征,融合在d个特征终选择一个最具有分类能力的变量,变量分类的阈值通过检查每一个分类点确定。
3)用抽取的特征进行构造随机森林模型。
4)输入数据,随机森林分类器对新的数据及逆行判别和分类,分类结果按照树分类器的投票多少而定。
随机森林中的每一棵树都是按照自顶向下的递归分裂原则,即从根节点开始依次对训练集进行划分。随机森林在试验中性能较好,由于随机性,使得随机森林不容易过拟合,有很好的抗噪能力并且可以处理很高维度的数据。但是在处理非平衡性数据集的时候,存在缺陷。选择的数据集是某矿区地质勘探得到的地震属性数据,数据标签分布较为均衡,因此该数据集适用于随机森林算法。
1.2 网格搜索
网格搜索(Grid Search CV),又被称作穷举搜索,是目前机器学习中很常用的一种寻优调参的方法。其基本原理是将变量区域网格化,遍历所有网格点,求解满足约束函数的目标函数值,最终比较选择出最优点。在随机森林算法中,每棵树的分类能力越强,整个森林的错误率越低;减小特征选择的个数,树的相关性和分类能力也会相应的降低,增大特征选择的个数,两者也会随之增大。所以关键是如何选择最优的特征个数。目前为止仍然没有单棵决策树的分类正确率和树的多样性两者之间的关系对随机森林性能影响的研究[14-15]。
基于经典的随机森林算法,提出一种改进的网格搜索优化算法。首先在较大范围内大步长划分网格,进行初步粗搜索选择出最优点;然后在最优点附近进行小步长划分网格,再次进行网格搜索出最优点。
随机森林中有2 个重要的参数,分别是决策树数目“n_estimators”和单棵决策树的最大特征数“max_features”,这两个参数能够较好的提升模型对噪声的处理能力,克服过拟合问题[16-18]。本研究选择这两个参数作为需要搜索的超参数,将二者组成参数对,进行搜索寻优(图2),最终利用网格搜索模型得分作为评估标准得到最优模型以及最佳参数。
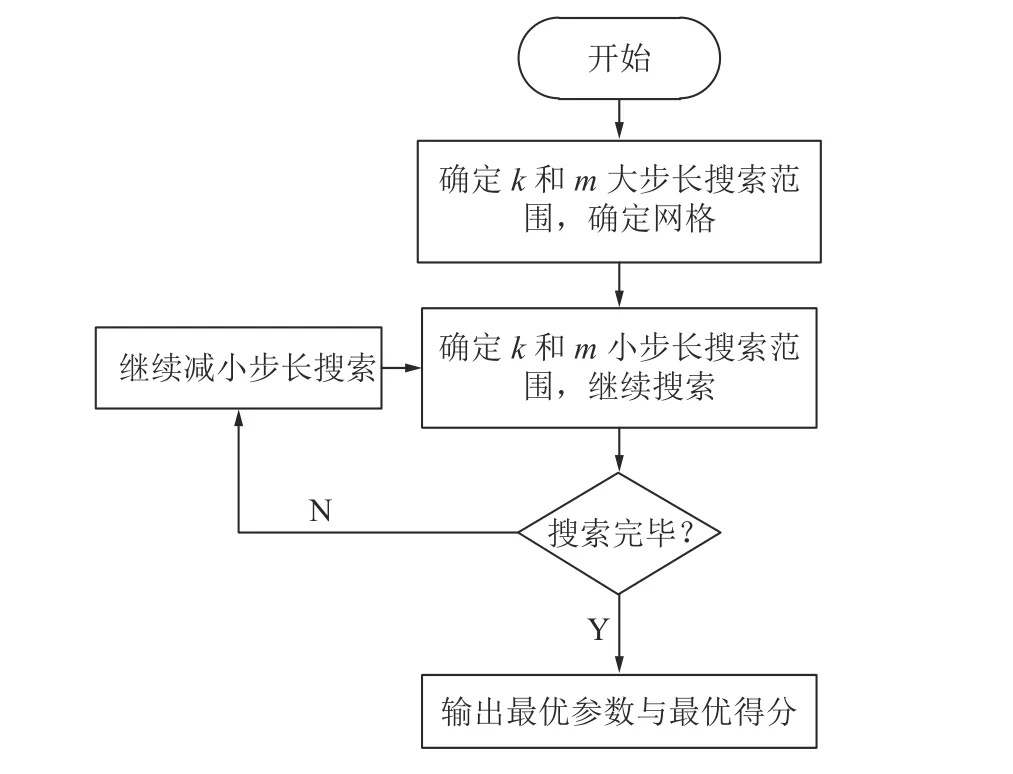
图2 改进网格搜索算法的寻优流程Fig.2 Optimization process of improved grid search algorithm
具体步骤如下:
1)确定决策树的数量k和最大特征数m的范围,设定大步长搜索范围。
2)大步长搜索结果确定小步长搜索范围,若输出的最优参数满足要求,则进行下一步,否则,缩小步长,重复上述步骤,继续搜索。
3)对网格节点上的每一组参数构建随机森林,选择得分最优的参数k,m。
随机森林通过网格搜索得到最优参数值,最优参数得到的模型可以使用网格搜索参数best_score,即模型的平均交叉验证得分来评估分类效果的好坏,得分越高表明该分类模型的分类效果更好。
2 基于优化随机森林算法的地质构造识别模型
以山西新元煤矿二条带二采区三煤层作为研究区域,该区域的地质异常体主要是断层,还含有较少的陷落柱。断层改变了煤岩层的埋藏条件,使煤层错断并发生显著位移,一方面破坏了煤层的连续性和完整性,为煤层开采带来阻力;另一方面,断层处容易发生瓦斯突水、透水等事故,严重影响矿区的安全开采[19-20];而陷落柱会破坏煤层的稳定性及连续性,减少煤炭资源储量,同时陷落柱的存在还影响了工作面的常规布置,给煤矿安全生产带来了重大的不利影响[21]。前期工程中利用地震勘探等地球物理探测方法得到的地震属性数据信息量非常大。由于不同的属性对相同目标体敏感度不同,针对特定目标体合理选择敏感度较高的属性数据进行分析有利于提高识别精度和结果的准确性[22]。
研究中利用三维地震勘探成果,按照5×5 网格提取出研究区域3 号煤层所对应的x、y坐标及相关属性数据,基于已有研究成果及专家推荐选取对构造敏感的十二种地震属性,根据矿方提供的实际揭露构造CAD 图,对该区域内的属性数据进行分类标记,将断层区域标记为2,陷落柱区域标记为1,无构造区域标记为0。经过属性敏感性测试,最后得到1 397 组包含x、y坐标以及标记的数据集,而且该数据集包含有12 种地震属性分别是:方差体切片、相干体切片、分频、均方根振幅、平均能量、倾角、曲率、瞬时相位、瞬时振幅、瞬时频率、最小振幅和最大振幅)。在算法改进以及模型构建过程中,首先对这12 种属性进行特征分析,之后进行优化网格搜索的随机森林模型的构建以及模型预测效果的验证。
2.1 特征分析
利用特征相关性分析与特征在随机森林算法分类效果中的影响二者结合对特征进行综合性分析。首先对12 种属性进行特征相关性分析,得到的属性间相关性见表1,相关系数越大,两个特征间的相关性越强,特征存在冗余,相关性越小则两个特征间的相关性越弱,当相关系数为0 时表明两个特征之间是独立的。之后在随机森林算法中,对属性进行特征重要性分析,确定这12 种属性对于分类器构建以及算法预测的重要性,见表2 与图3。依据特征间的相关性分析与特征重要性分析来选择特征。
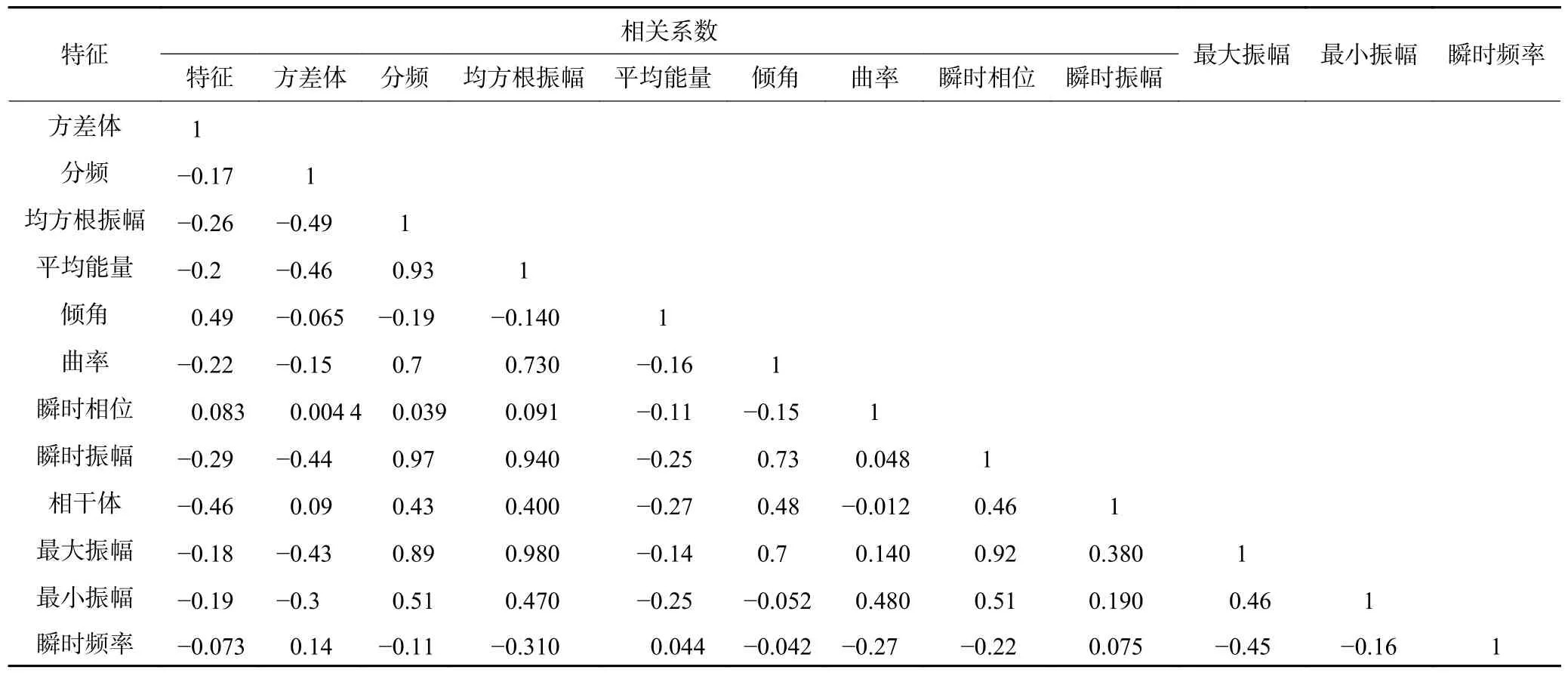
表1 特征相关性分析Table 1 Feature correlation analysis
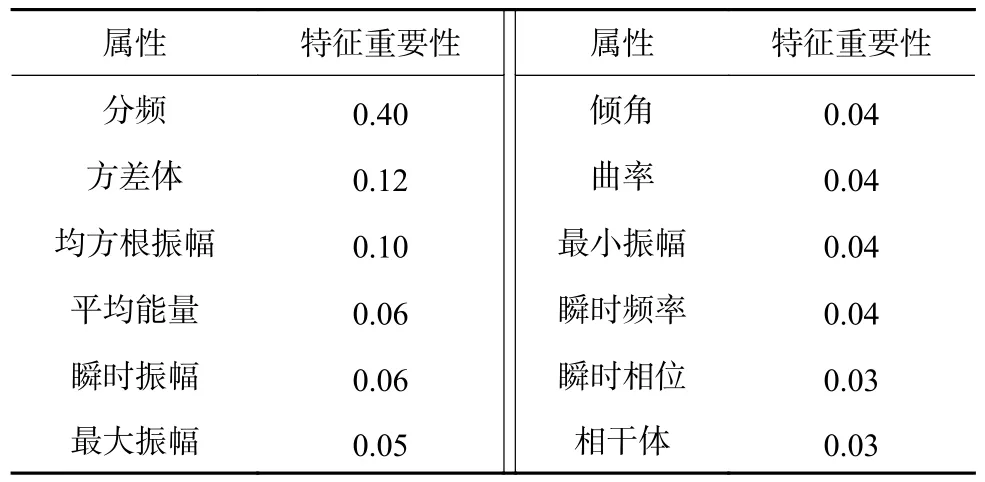
表2 特征重要性Table 2 Feature importance
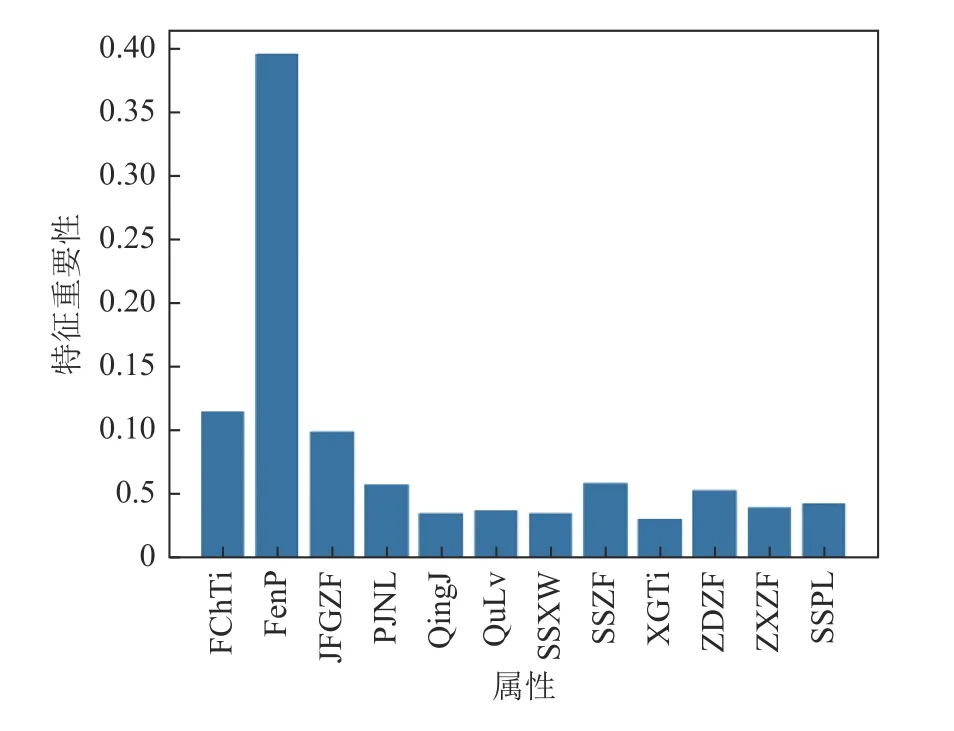
图3 地震属性特征重要性Fig.3 Importance of seismic attribute feature
本数据集中特征相关性分析见表1,可以看到最大振幅与平均能量、瞬时振幅与均方根振幅之间相关性较大,而从表2 和图3 中可以看到,不同的特征对于分类效果的影响不同,且这4 种属性间的特征重要性差距不大。经过进一步的算法测试对比试验,发现4 个特征对本数据集分类效果影响都比较大,而且删掉其中某一个特征后,算法预测的准确率会下降(约下降3%),且本数据集特征较少,因此选择保留原本12 个特征进行后续的算法优化。
2.2 算法流程
首先对分类器数量进行大步长搜索,设定随机森林分类树的数量n_estimators 初始搜索范围为[50,1 000],步长设置为50,设定max_features 的范围为[1,12],步长为1。利用Python 中的模型得分参数对模型进行评估,大步长搜索过程中模型得分受2 个参数影响的曲线如图4 所示。小步长搜索过程中模型得分受2 个参数影响的曲线如图5 所示。

图4 大步长搜索模型得分Fig.4 Large step search model score
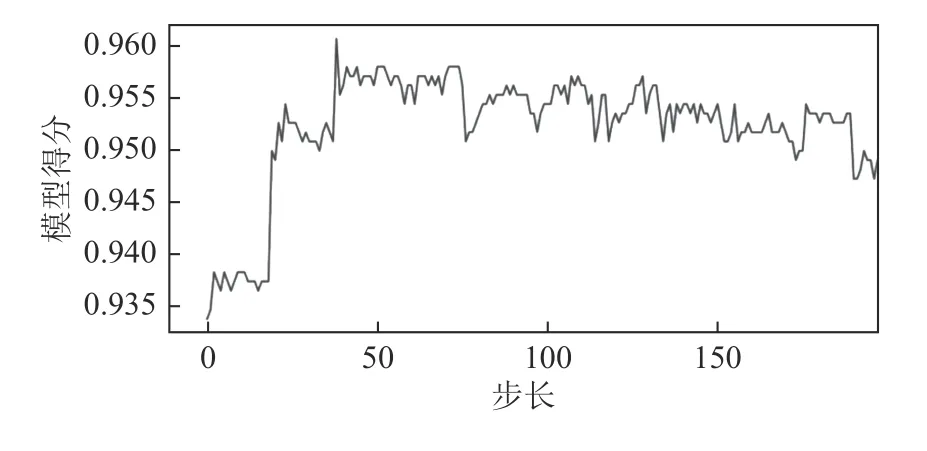
图5 小步长搜索得分Fig.5 Small step search scores
由图4 中曲线峰值为0.960 5,输出参数值('max_features':3,'n_estimators': 50)。而且从图4 中可以看到,当基分类器的数目超过一定值时,模型的得分基本收敛,再增加基分类器的数目,效果基本不会提升,而且代码运行速度会变慢。
下一步进行小范围搜索,初步设定n_estimators 的范围为[1,100];max_features 的范围为[1, 12]。得到最优参数对('max_features':3,'n_estimators': 58)。由于参数数据较多,因此在本论文中选择最优参数点附近的20 组数据作为参考,见表3。当分类器数目为58,最大特征数为3 时,模型得分最高为0.963 3。
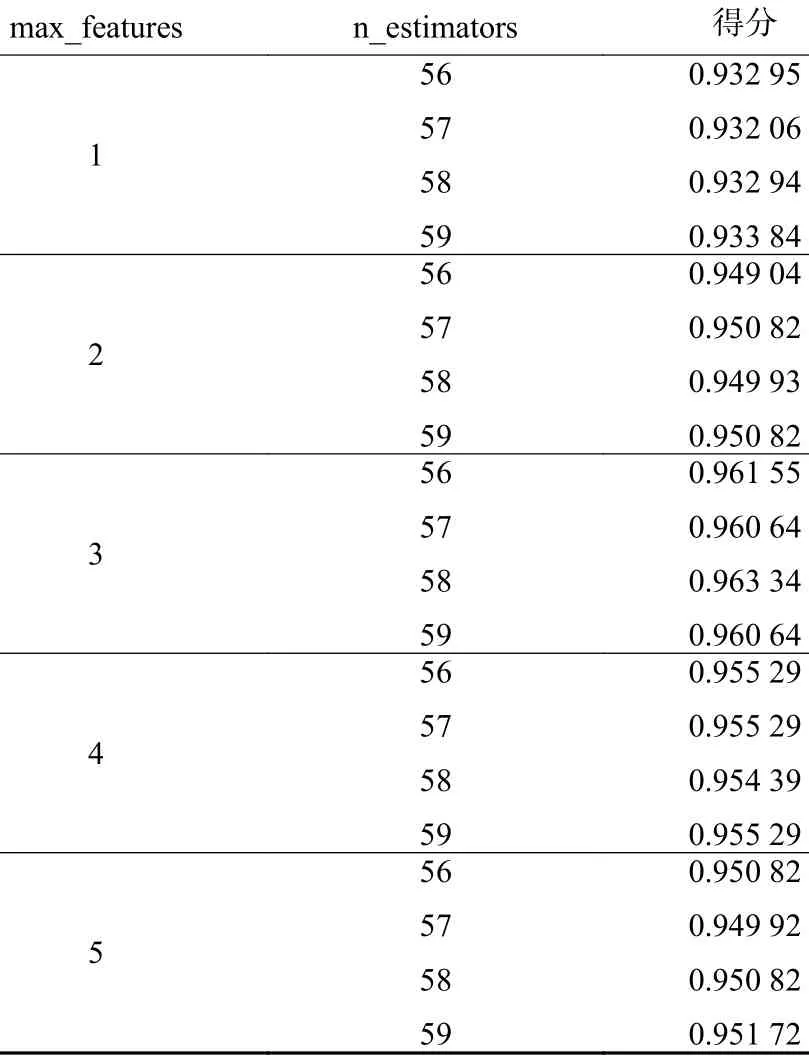
表3 参数对及得分Table 3 Parameter pairs and scores
2.3 算法验证
为进一步验证模型的可靠性,利用实地采集并且经过处理后的其他几个开采区域的地震属性数据集进行验证。在进行验证时,为了节省工作,直接进行大步长(步长设定为50)网格搜索,初步得到较优分类器数目,进行第二步小范围搜索(步长设定为10),得到更加精确的分类器数目取值,最后进行步长为1 的细化分,得到最终模型参数以及参数。各数据集在改进网格搜索的随机森林模型中的得分见表4。可以看到,经过改进后的随机森林算法模型精确度均有不同程度的提高。

表4 随机森林参数优化算法验证Table 4 Validation of optimization algorithm for random forest parameters
将改进后的随机森林算法与GBDT(Gradient Boosting Decision Tree,梯度提升树)、逻辑回归、决策树等3 种算法在本数据集上的预测结果进行比较,在比较预测分类效果时,为了对分类器的评估更全面,利用正确率、准确率和f1score 等评估指标来评估模型的分类效果。
在训练样本中,真阳性(True Positive,TP):指被分类器正确分类的正例数据;真阴性(True Negative,TN):指被分类器正确分类的负例数据;假阳性(False Positive,FP):被错误地标记为正例数据的负例数据;假阴性(False Negative,FN):被错误地标记为负例数据的正例数据。
针对全体训练样本,正确率(Accuracy,A)计算方式为
针对正例:准确率P计算公式为
召回率R的计算公式为
f1score 被定义为准确率和召回率的调和平均数,用它来综合评估模型性能调和平均数:
结果见表5。可以看到相比于其他算法,改进后的随机森林算法模型预测准确率更高,而且从算法正确率A、准确率P、f1score等得分来看,模型的分类效果得到了相应的提高。
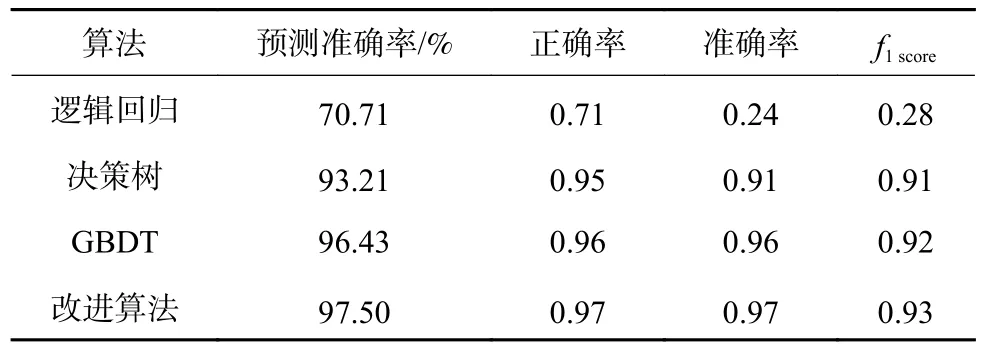
表5 算法对比Table 5 Algorithm comparison
3 模型验证
利用改进后的随机森林算法模型进行构造识别预测。依据矿方提供的新元煤矿二条带二采区实际揭露后的勘探成果,按照1∶5 000 比例尺绘制得到该区域的实际揭露构造CAD 图,如图6 所示。构造图中,断层为线(图6 中紫色线),陷落柱为面(图6 中红色面区域),蓝色线部分为开采划定的巷道。从图6可以看到,该区域中主要构造为断层,陷落柱比较少。
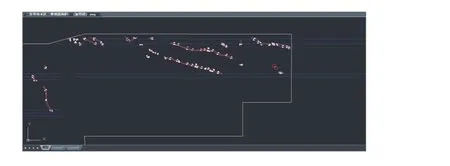
图6 二条带实际揭露构造CAD 图Fig.6 CAD drawing of actual exposed structure of the second belt
研究中将地震属性数据按照7∶3 的比例划分为训练集和测试集对模型进行训练以及预测。预测得到地震属性数据坐标点以及标记类型文件,利用课题组开发的软件进行识别结果显示,模型预测呈现出来的图中断层为线,陷落柱为面,得到识别结果如图7 所示。
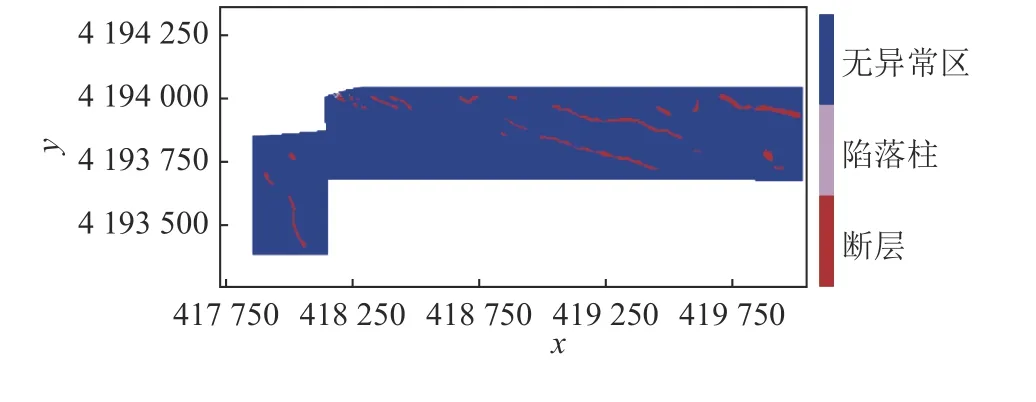
图7 预测构造Fig.7 Prediction structure
与该区域勘探得到的三维地震构造CAD 图(图6)进行对比,可以看到预测得到的结果中,构造数量预测较为准确,而且预测生成的文本文件中构造对应的坐标点比较精确,可以有效地预测该区域构造所处地理位置,且进行有效识别。
为了进一步验证模型,利用新元北采区西部地震属性数据进行验证,该矿区的三维地震构造如图8 所示,该验证矿区中陷落柱构造较多,断层较少。得到的构造预测如图9 所示,改进后的算法模型预测得到的结果与该矿区构造类型基本一致而且通过对生成文本文件中的数据对比观察到坐标基本符合。二条带采区断层构造较多,陷落柱构造较少;而北采区西部矿区陷落柱构造较多,断层构造相对较少。但是通过试验结果,可以看到该算法模型对于断层和陷落柱都有较准确地识别效果。
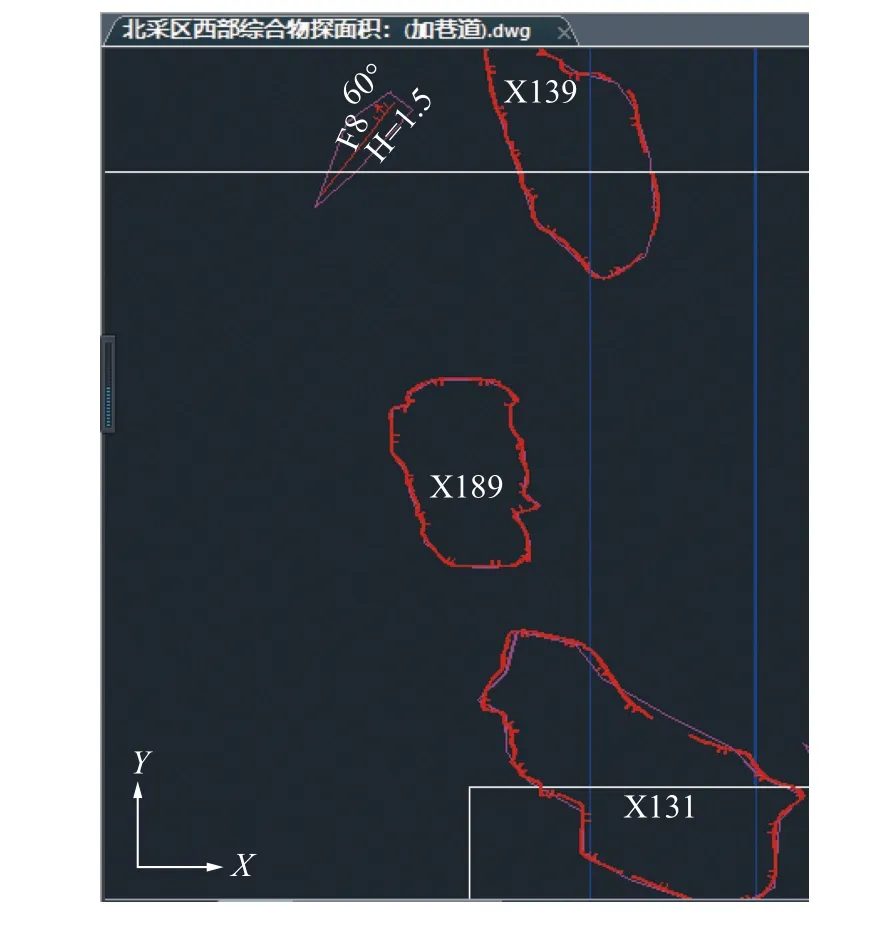
图8 北采区西部实际揭露构造CAD 图Fig.8 CAD drawing of actual exposed structure in the west of North Mining Area
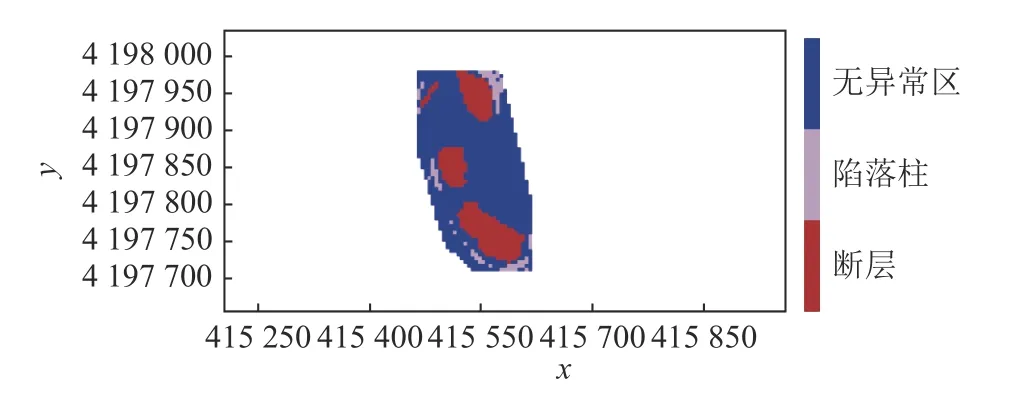
图9 验证矿区构造预测结果Fig.9 verification of structural prediction results of the mining area
4 结 语
利用山西新元煤矿二条带二采区三维地震勘探成果提取到的地震属性数据集(感谢矿方与勘探方提供的数据),针对现有的研究中对地震属性数据集要求较高且数据处理较复杂的问题,基于经典的随机森林算法模型,提出了一种改进网格搜索优化随机森林算法模型的方法。通过对网格搜索进行分步长搜索,对参数对进行调整,利用改进后的随机森林算法对地震属性数据进行融合分类预测,进而建立地质构造识别模型。将该算法模型与逻辑回归、决策树、GBDT 等几种算法模型进行比较,在模型预测准确率、算法正确率、准确率、f1score 等评估标准进行比较证明该算法优于其他机器学习算法。而且经过在新元北采区西部地震属性数据集上的测试,验证了该算法模型在断层和陷落柱等构造识别中分类结果的准确性与适用性。
