核磁共振陀螺横向补偿磁场优化设计
2023-05-31明泽额尔顿岳亚洲
明泽额尔顿, 岳亚洲, 李 攀, 雷 兴, 张 昊
(西安飞行自动控制研究所,陕西 西安710065)
0 引言
核磁共振陀螺(NMRG)是一种利用核磁共振原理工作的全固态陀螺仪[1-3],没有运动部件,性能由原子材料决定,理论上动态测量范围无限,综合运用了量子物理、光、电磁和微电子等领域中的技术,是未来陀螺仪发展的新方向[4-6]。
原子自旋可在惯性参考系中保持其初始指向,类似于传统机械陀螺中的转子,所以原子自旋也可用于敏感转动。20世纪60年代,欧美国家已开始研究核磁共振陀螺。1979年,Litton公司和Singer-Kearfott公司分别开发了核磁共振陀螺原型机,均达到了导航精度[7-8],虽然结果较好,但核磁共振陀螺项目仍在其潜力被完全认识前中止了,因当时认为激光陀螺技术更有前途。

核磁共振陀螺通过检测磁场中原子核自旋进动频率的改变确定载体角速度,工作原子通常约束在由耐碱金属腐蚀的玻璃制成的气室内。陀螺所涉及的磁场包括纵向静态磁场和横向振荡磁场,原子核自旋绕静磁场进动,振荡磁场频率与原子核进动频率相同。在进行陀螺设计时,必须保证静态磁场纵向分量在气室范围内均匀分布,横向分量近似为0;振荡磁场横向分量在气室范围内均匀分布,纵向分量近似为0。从陀螺原理可看出,核磁共振陀螺的陀螺精度与静磁场的均匀性、稳定性密切相关。
在典型的实验室磁场(1~10 T)中,大多数核自旋相应的拉莫尔频率在10~100 MHz内[13-17],此值必须与用核磁共振陀螺检测的典型旋转速度匹配,以地球自转速率ωearth=7.27×10-5rad/s为参考,此旋转速率约比典型实验室中的普通拉莫尔频率小12~13个数量级。如果核磁共振陀螺需要检测出低于地球自转3~4个数量级的角速度,则静磁场数量级要求更低。为保证静磁场的稳定性,即使对陀螺进行了磁屏蔽,磁屏蔽罩内的电路、引线、线圈仍会产生杂散磁场干扰到净磁场的稳定性。所以需要对陀螺进行磁补偿。
1 核磁共振陀螺横向磁补偿系统
核磁共振陀螺的磁补偿系统通常可分为被动磁屏蔽和主动磁补偿两部分。被动磁屏蔽主要通过磁屏蔽装置,一般可实现5~6个数量级的屏蔽系数[18],但这比导航级核磁共振陀螺要求(10-15T)少4个数量级,需通过主动磁补偿进行反馈抑制。
在敏感轴方向,采用双核素可实现z轴杂散磁场的提取,根据杂散磁场的大小在静磁场线圈施加补偿磁场电流,从而实现纵轴磁场的补偿。横向磁场补偿则需在纵轴施加载波磁场,并对探测信号进行解调,得到2个方向的杂散磁场,之后通过横向补偿线圈进行补偿。
一般由于静磁场均匀性与陀螺性能高度相关,在核磁共振陀螺设计中会优先保证静磁系统的设计。而横向补偿线圈由于重视性不够及结构和体积的限制,很难实现高均匀度的要求。
目前,由于多数核磁共振陀螺采用圆柱体设计,磁屏蔽罩为圆柱形,为便于安装调试,横向补偿线圈设计为马鞍形亥姆霍兹线圈。
1.1 马鞍形亥姆霍兹线圈
马鞍形线圈的结构如图1所示。图中,I为线圈电流,L为线圈长度,W为线圈宽度,D为线圈间距,R为弧形线圈的半径,Θ为弧形线圈对应的圆心角。经过简单计算可得:
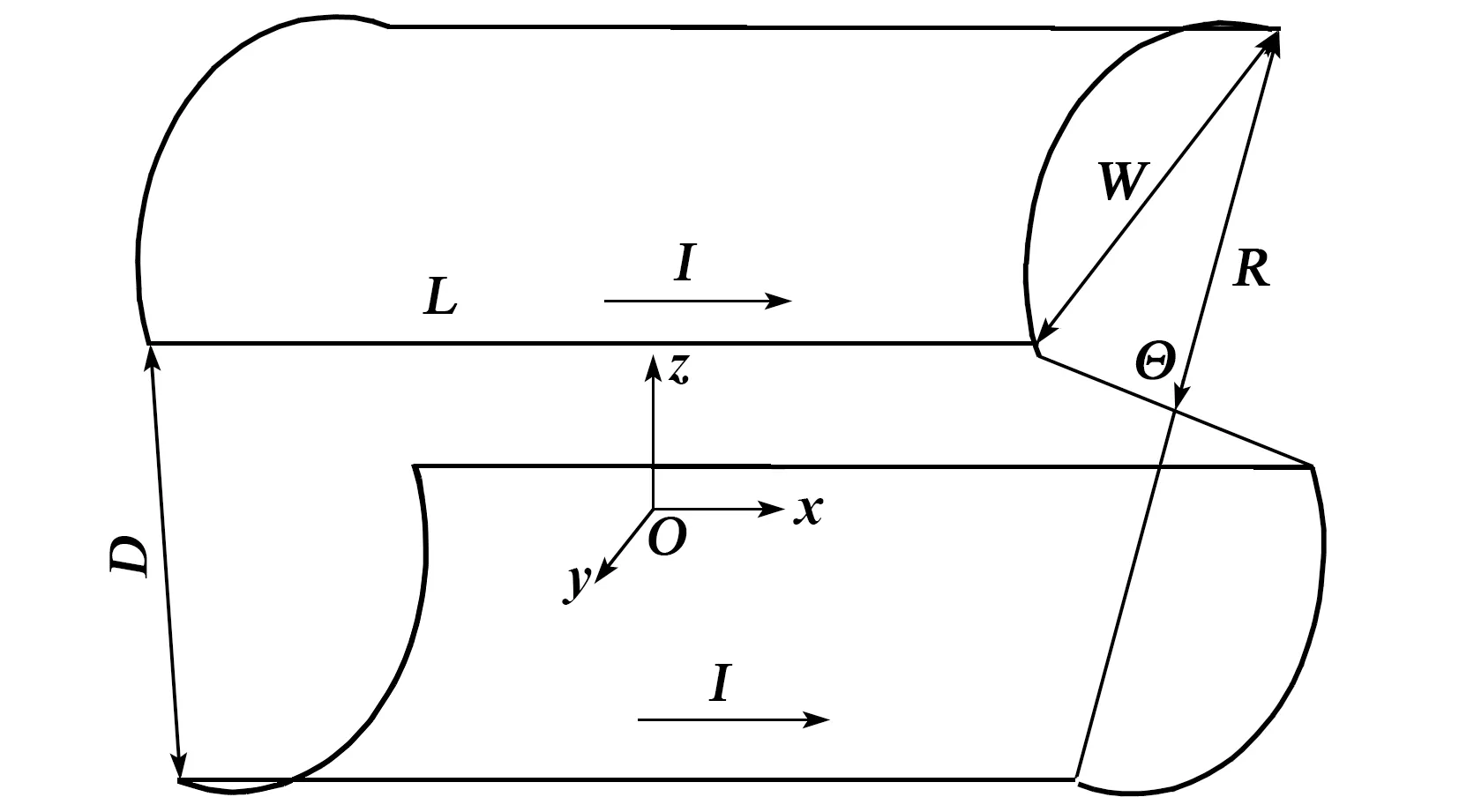
图1 马鞍形亥姆霍兹线圈
W=2Rsin(Θ/2)
(1)
D=2Rcos(Θ/2)
(2)
为便于计算,可将鞍形线圈拆为两部分,一部分包含4根直导线,另一部分包含4个弧形线圈。
1.2 4根直导线产生的磁场
考虑无穷长直导线产生的磁场。设一点P,其与导线的垂直距离为r0,向直导线引垂线,垂足为O,如图2所示。
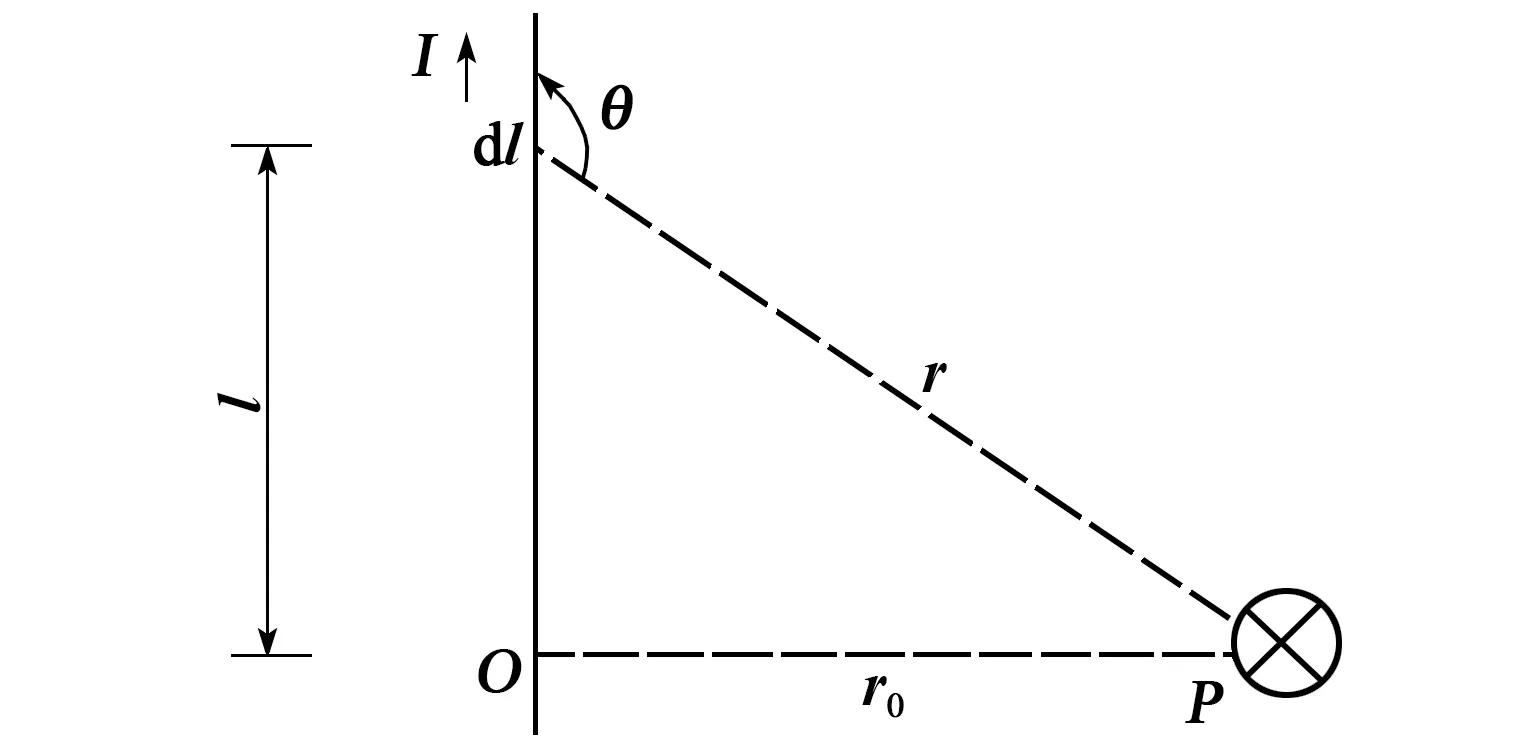
图2 直线电流的磁场
根据毕奥-萨伐尔-拉普拉斯定律,任意电流元Idl(其中,l为电流元到O的距离)在点P产生的磁场垂直纸面向里,其大小为
(3)
式中:μ0为真空电导率;B为磁感应强度;θ为电流元Idl到点P的连线与导线间的夹角;r为点P与电流元Idl的间距。从而可以得到有限长度导线在P点产生的磁感应强度为
(4)
式中θ1,θ2分别为P点到导线两端的引线与导线所成的夹角。
考虑4条直导线的合磁场,在z轴上任选一点P(0,0,Z),此时P点的磁感应强度如图3所示。其中Bzi为第i条导线在P点的磁感应强度。

图3 4条直导线的合磁场
利用式(4)可得P点的磁感应强度为
(5)
式中Z为点P在z轴上到中心点的距离。将式(1)、(2)代入式(5)可得:
(6)
对于x方向,由于直导线与x轴平行,在该方向不产生磁感应强度,所以Bx=0;对于y轴方向,由图3可看出,4根直导线在y轴方向产生的磁感应强度相互抵消,所以By=0。
1.3 4根弧形导线产生的磁场
载流环形线圈如图4所示。以线圈中心为坐标原点建立直角坐标系,x轴与线圈平面垂直,电流I以逆时针方向绕x轴旋转。根据毕奥-萨伐尔-拉普拉斯定律,任一电流元Idl在点P形成的磁场可表示为

图4 环形电流磁场
(7)
式中:r为元电荷指向点P的矢量;μ0为真空电导率。
由式(7)可得:
(8)
对于弧形导线,计算方法与其类似,由此可得:
(9)
图5为4根弧形导线产生的磁场。对于图5所示的4根弧形导线有:

图5 4根弧形导线产生的磁场
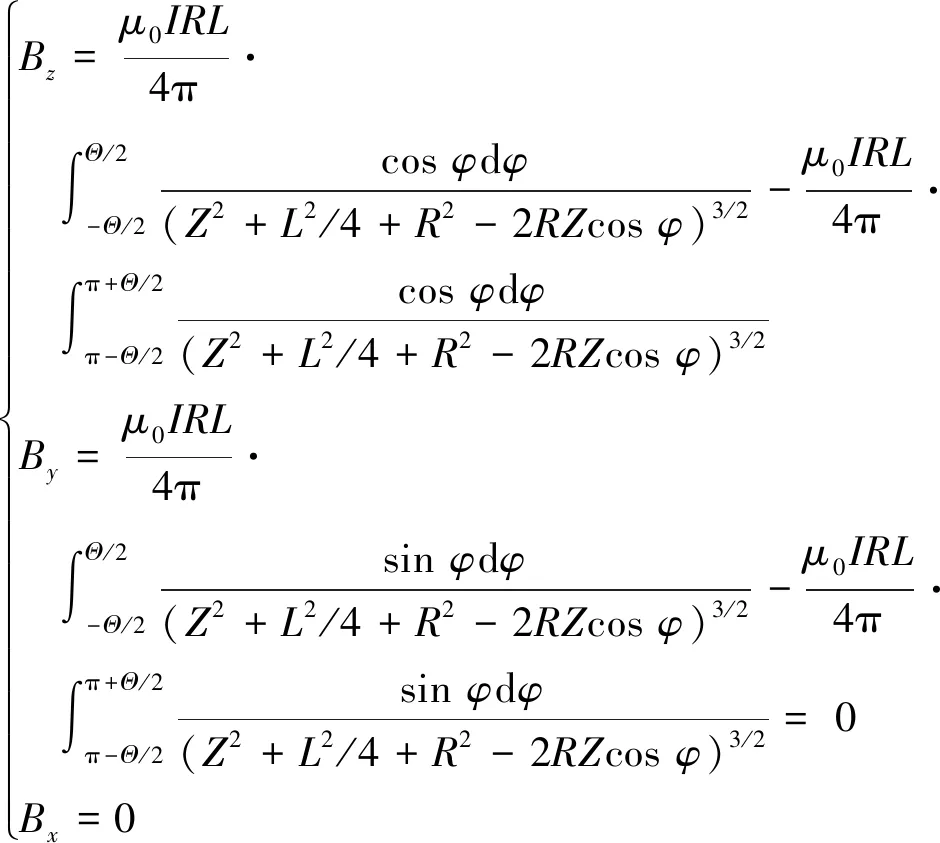
(10)
1.4 马鞍形线圈产生的磁场
马鞍形线圈产生的磁场为
(11)
利用Matlab 进行仿真可得横向磁场线圈的初步设计结果:I=0.2 A,R=85 mm,L=73.7 mm,Θ=45°,取气室尺寸范围内计算磁场非均匀性指标δ=0.009 5,沿z轴的磁场如图6所示。
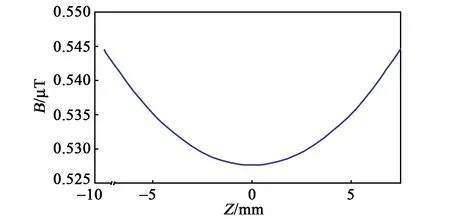
图6 线圈初步设计
2 线圈优化设计
2.1 参数分析
本文对马鞍形线圈的各项参数进行优化设计。首先固定其他尺寸,改变半径R,以确定R对磁场非均匀性δ的影响,如图7所示。由图可看出,大趋势上磁场非均匀性δ随R增加而逐渐减小。
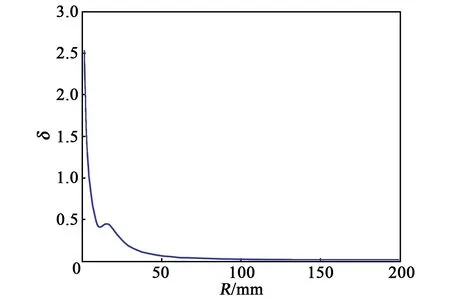
图7 R对磁场均匀性的影响
固定其他尺寸,改变线圈长度L,以确定L对磁场非均匀性δ的影响,如图8所示。由图可看出,磁场非均匀性δ在L=14 mm处达到极大值,随后逐渐减小,直至L≈300 mm,随后趋于振荡。
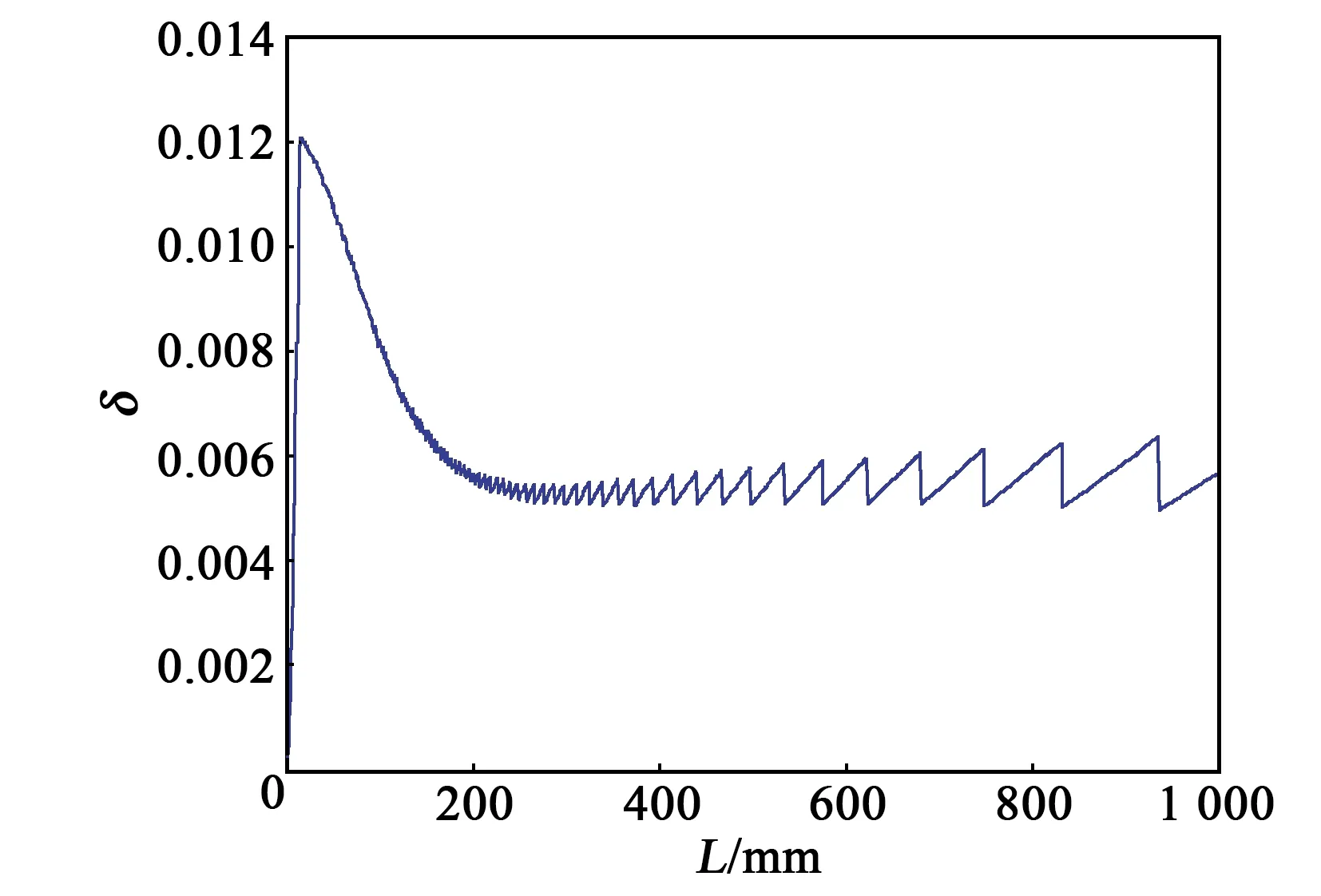
图8 L对磁场均匀性的影响
固定其他尺寸,改变角度Θ,以确定Θ对磁场非均匀性δ的影响,如图9所示。由图可看出,磁场非均匀性δ随Θ增加而逐渐减小。
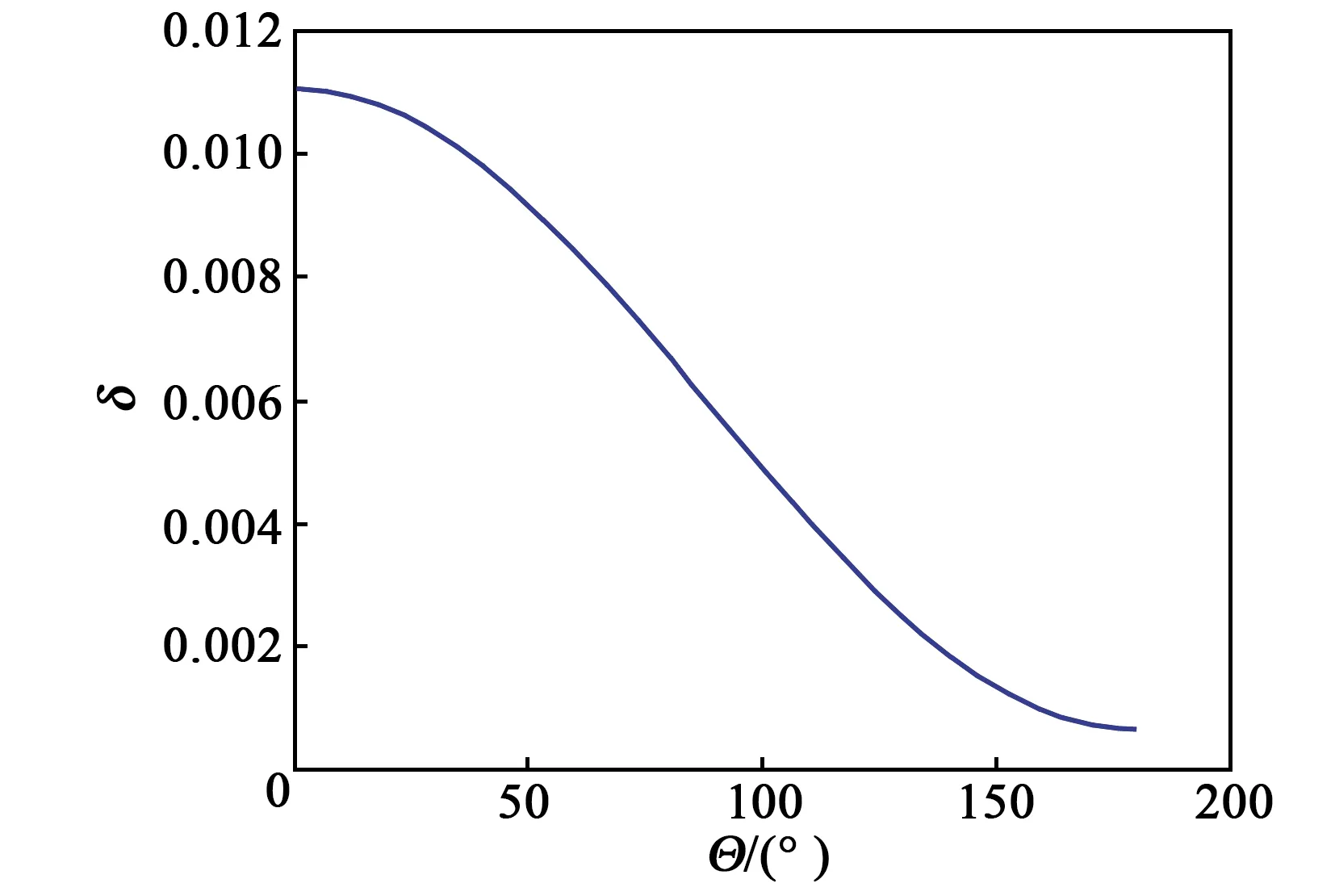
图9 Θ对磁场均匀性的影响
2.2 参数优化
综上分析可看出,弧形线圈半径R、线圈长度L、弧形线圈张角Θ都会影响横向补偿线圈的磁场均匀性,可通过回归分析的方法建立上述参数与横向补偿线圈的磁场均匀性之间的回归关系。
为降低计算量并提高回归精度,考虑到使用简单的一次回归正交设计不能得到满意的结果,故采用最优近似饱和设计进行二次回归。取R、L、Θ作为3因子,采用最优近似饱和设计(R311D)进行回归设计,各因子的编码自变量(xi)的设计水平j和实际自变量(zi)的实际水平如表1所示。

表1 最优近似饱和设计试验因子及水平
表1中,±2水平代表设计指标的上下限。本文由于考虑到实际陀螺结构,R至少大于陀螺光具座的半径,但不超过光具座半径的1.2倍;L不大于光具座总长。考虑到实际加工的难度,要求10°≤Θ≤175°。实施水平间距Δi为
(12)
设计水平j对应的实际水平为
zji=z-1i+Δi(xji-x-1i)
(13)
具体数值如表1所示。使用Matlab进行仿真计算,以产生磁场的非均匀性指标δ为判定条件,得到结果如表2所示。
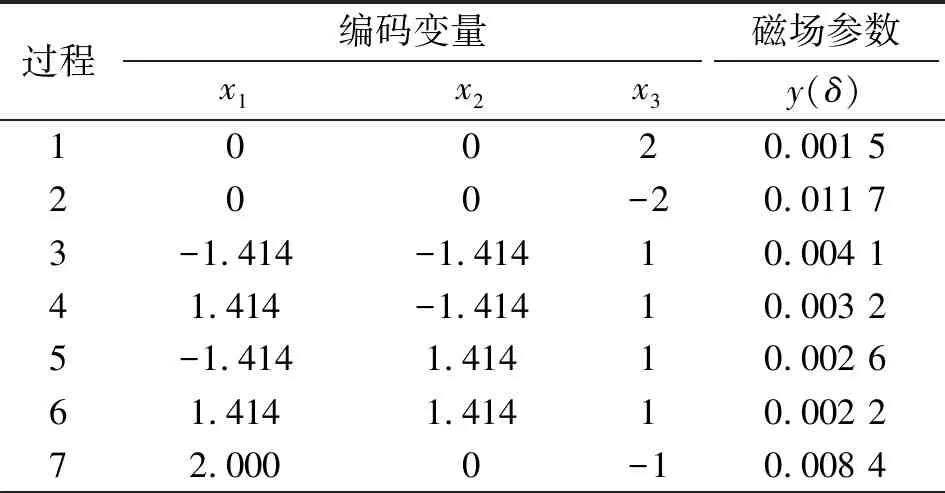
表2 试验方案及结果
使用下列模型进行二次回归:
(14)
式中:n为自变量的数目;b0为回归方程的常数项;bi为一次项的偏回归系数;bij为二次项的偏回归系数。
使用Minitab进行多轮数学回归。若数学回归的结果中有系数未达到显著水平(p<0.05),将其并入误差项继续进行回归,直到得到最终的回归方程。
对于磁场参数y(磁场的非均匀性指标δ),从最终回归的方差分析表(见表3)可看出,回归达到极显著水平(F>F0.01(3,7)=8.45),回归方程的复相关系数Rsq=0.957;偏回归t检验中,所有系数均达到极显著水平(p<0.01),如表4所示。

表3 试验方差分析

表4 偏回归系数b的t检验
回归方程为
y=0.006 46-0.000 527x1-
0.000 509x2-0.002 98x3
(15)
使用遗传算法进行优化可得到最优点位于(-0.489,1.841,1.94)水平,对应R=91.42 mm,L=77.62 mm,Θ=172.53°,此时回归结果为δ=3.62×10-10,仿真结果为δ=6.49×10-4,产生的轴向磁场如图10所示。调整I=0.084 8 A,方便与优化前对比。图11为优化前后横向补偿线圈的磁场分布。由图可看出,线圈均匀性显著提高。
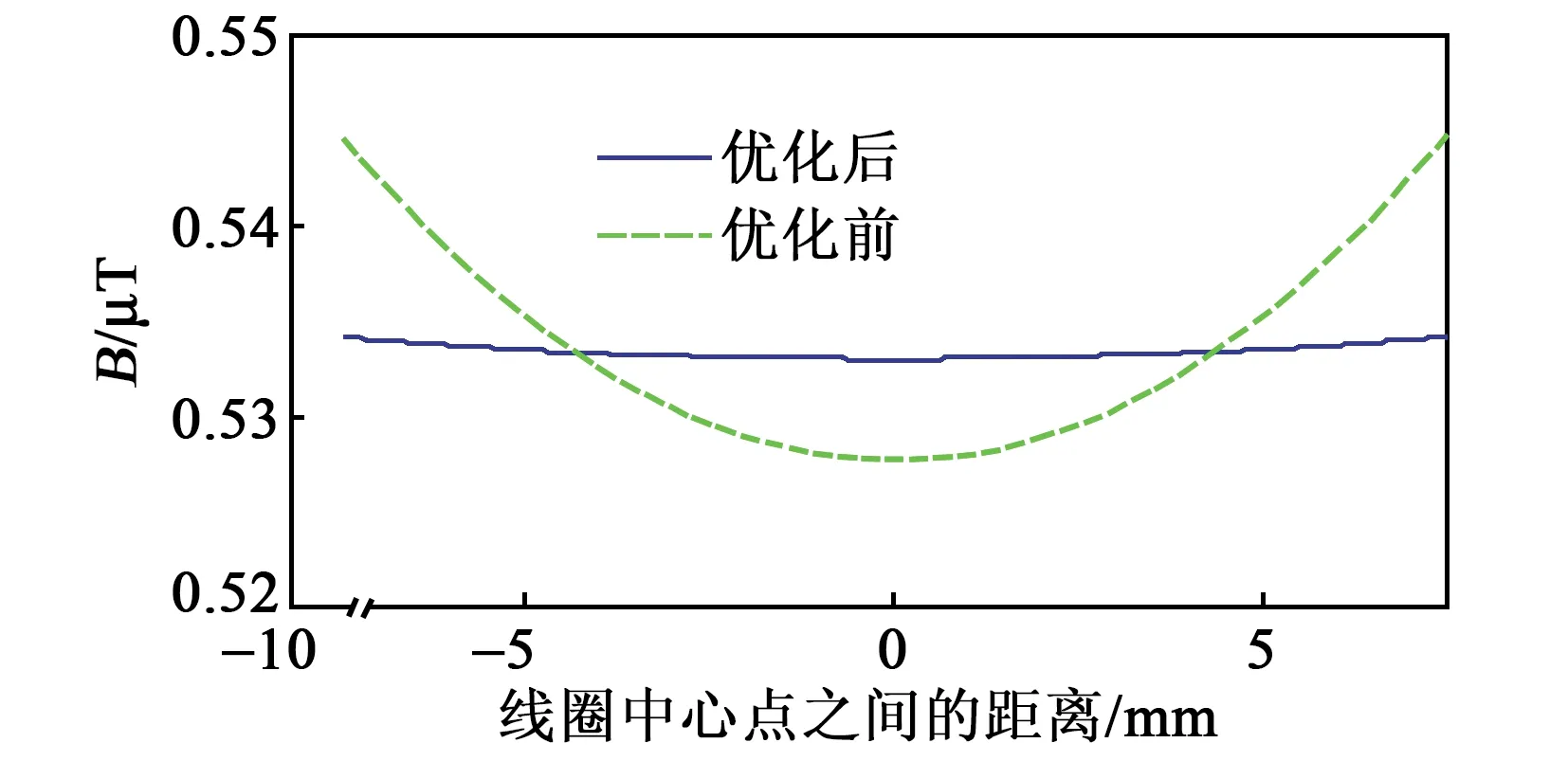
图11 优化前后横向补偿线圈的磁场分布
3 结束语
作为一种新型微型陀螺仪,随着微机电系统(MEMS)技术和微型原子器件的发展,核磁共振陀螺仪有望在中高精度导航和制导领域得到应用,其潜在应用方向包括小型飞行器、无人飞行器、无人水下潜艇、地面车辆及战术导弹等。
本文从核磁共振陀螺磁场分布的理论分析出发,通过数学计算和计算机仿真分析研究了横向磁补偿线圈的磁场分布,并对横向磁补偿线圈进行了优化设计。设计的核磁共振陀螺横向磁补偿系统磁场均匀性较优化前提高近13倍,满足核磁共振陀螺的使用需求。该工作为核磁共振陀螺仪设计和制造提供了一定的理论依据和参考价值。
