基于铌酸锂/BCB/聚酰亚胺结构的柔性声表面波器件的设计与仿真

陈健中,彭 斌,张万里,林庚辉,高令桥

(电子科技大学 电子科学与工程学院,四川 成都 611731)

0 引言

声表面波(SAW)传感器具有体积小,结构简单,易于制造,成本低等优点,可以对应变、温度、扭矩、气体浓度及液体流量等物理量进行感知[1-4]。SAW传感器可应用于如汽车、航空航天、核电和发电行业等[5-8]领域。目前研究较多的SAW传感器大部分都是基于压电单晶块材[5,9],或沉积在硅、蓝宝石等刚性衬底上的压电薄膜[10-11]制备,在某些特殊场合(如曲面工件的表面测温)难以应用,同时,由于衬底较厚,将导致其测试应变时灵敏度较低,故需要发展基于压电薄膜的柔性SAW传感器。

铌酸锂(LiNbO3,LN)的压电系数大,化学稳定性好,机械品质因数高,机械加工性能好,是制备SAW器件的优异材料[12]。近年来,离子注入剥离(CIS)技术可在保持材料良好性能的基础上制备厚度为亚微米量级的LN单晶薄膜[13-14],为制备基于LN的柔性SAW传感器提供了新的思路。

聚酰亚胺(PI)薄膜具有良好的柔性,且与电子器件中常见的电极粘接层材料铬或钛的附着力高。因此,PI常用作柔性电子器件中的柔性衬底[15],可利用CIS技术在柔性PI衬底上制备单晶LN薄膜,进而研发柔性SAW传感器。但这种压电薄膜/柔性衬底结构的SAW器件研究较少,柔性衬底与键合层介质对SAW器件性能的影响尚不清楚,因此有必要对该结构的SAW器件进行仿真研究。

本文采用有限元法针对“LN/苯并环丁烯(BCB)/PI”3层膜结构的柔性SAW器件(BCB作为LN与PI衬底的键合介质)进行了仿真研究。

1 模型与仿真过程

SAW器件(见图1)由叉指电极与压电衬底构成,其中叉指电极具有周期性结构。本文选择周期λ作为仿真单元,其模型如图2 所示。在该模型中,整个模型的宽度为λ,金属电极厚为0.005λ。虽然实际器件中PI的厚度可能大于3λ,但考虑到瑞利波能量只集中在距离表面2λ内,因此,在该模型中PI衬底厚度取3λ。仿真结果发现,增大PI厚度对仿真结果影响较小。对边界Γ1～Γ6设置周期性条件,对边界Γ10设置固定约束边界条件。仿真中所用材料参数如表1、2所示。利用该模型通过仿真可获得SAW器件谐振时的振型图,并计算该结构中SAW的声速v和机电耦合系数k2。

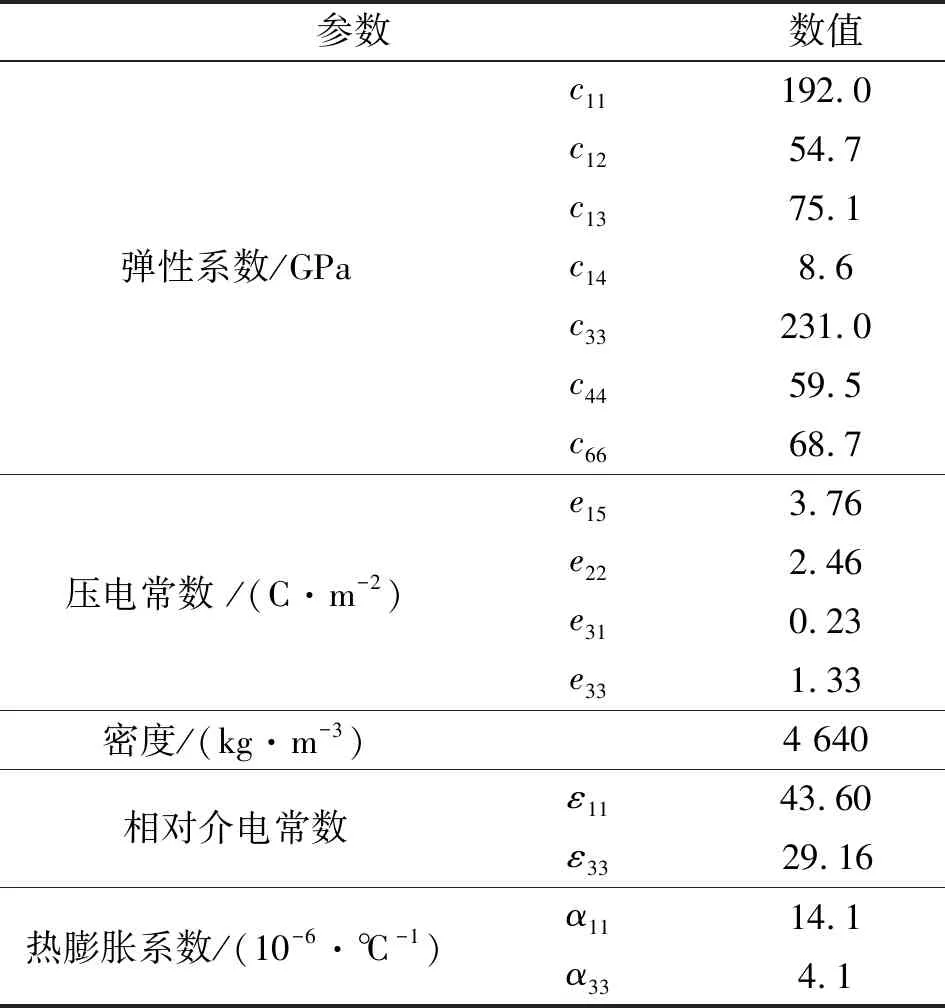
表1 仿真所用LN的材料参数[16]

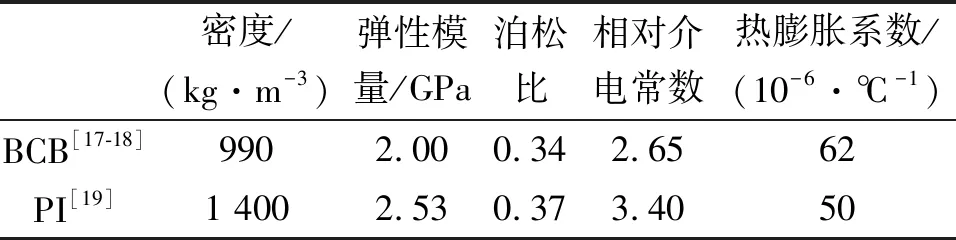
表2 仿真所用BCB与PI的材料参数

图1 LN/BCB/PI结构的 SAW器件

图2 LN/BCB/PI结构SAW器件的二维仿真模型

为了研究温度对该结构SAW器件性能的影响,本文不仅考虑材料的热膨胀特性,同时也考虑温度变化引起的材料弹性系数变化。由于金属电极很薄,其影响可忽略。LN的弹性系数随温度变化关系可参考文献[16]。PI的弹性模量(EPI)随温度(T)变化关系:

EPI=-0.005 33×T+2.666

(1)

由于BCB和PI同属于高聚物,性质相似,可以假设BCB弹性模量(EBCB)的温度系数与PI相同,即:

EBCB=-0.005 33×T+2.133

TDR是时间域反射技术(Time Domain Reflectometry)的简称，和雷达原理相似，也被称作“闭路雷达”。不同的是它使用同轴电缆作为信号的传输介质，通过TDR测试仪向埋入滑坡检测孔内的同轴电缆发射脉冲信号，当滑坡岩土体发生位移将使同轴电缆产生局部剪切和形变时，该部特性阻抗改变，信号发生反射与透射并反映于反射信号之中，分析反射信号的返回时间和反射系数等特性可确定形变的程度和发生位置，达到监测的目的。一个完整的TDR滑坡监测系统由电源、TDR同轴电缆、数据记录仪、电缆测试仪、远程通讯设备以及数据分析软件等部分组成[36](图5)。

(2)

假设在研究的温度范围内,LN、BCB和PI的热膨胀系数均不随温度改变而改变,则LN、BCB与PI的密度[16]分别为

(3)

(4)

(5)

式中:T0=25 ℃为参考温度;ρ0,LN,ρ0,BCB,ρ0,PI分别为LN、BCB、PI在T0时的密度;α11,α33分别为LN沿着y、z轴的线性热膨胀系数;αBCB,αPI分别为BCB、PI的热膨胀系数。

2 结果和讨论

2.1 LN、BCB厚度对SAW器件的影响

图3为BCB厚度hBCB不同时SAW器件声速随LN薄膜厚度hLN的变化曲线及振型图。由图3中的振型图可看出,不同BCB厚度对声速的影响较小,这可能是因为BCB和PI衬底性质类似,其弹性系数和密度相近,BCB中的声速(约841 m/s)和PI中的声速(约760 m/s)也相近。

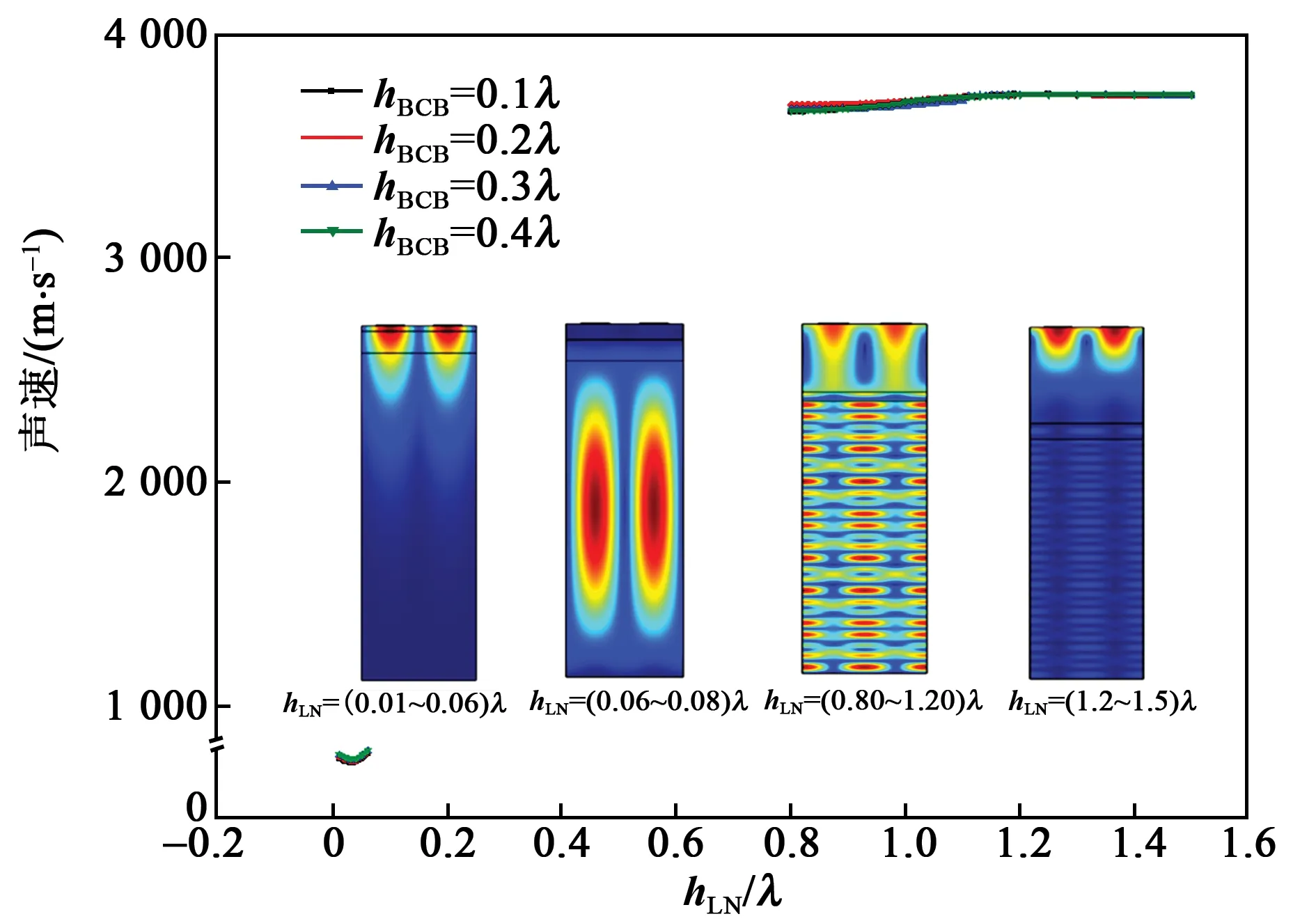
图3 不同LN与BCB厚度下SAW器件中的声速

由图3还可发现,器件的声波振动模式可分成4个范围进行分析:

1) 当hLN=0.01λ～0.06λ时可激发稳定的瑞利波模式,声速由约770 m/s增加到约794 m/s,与BCB、PI中声速接近。这是由于LN薄膜很薄时,声波主要在BCB/PI结构中传播,随着LN厚度小幅增加,在LN薄膜中传播的声波能量增大,此时声速有小幅增加。

2) 当hLN=0.06λ～0.8λ时,因为表面波和体波耦合,声波能量基本被束缚在PI衬底内部,器件表面处无振动,不能形成瑞利波模式。

4) 当hLN>1.2λ时,稳定的瑞利波模式再次被激发出来,此时几乎无声波能量进入PI衬底中,声速约为3 735 m/s,且随着hLN增大,声速基本保持不变,接近LN的声速(3 980 m/s[20])。

图4为器件机电耦合系数k2和hLN的关系。由图3中可知,hBCB对SAW器件性能影响不大,所以图4中仅给出了hBCB=0.2λ时的情况。

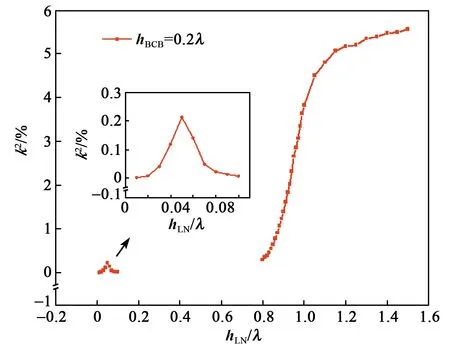
图4 不同LN厚度下SAW器件中的机电耦合系数

器件的机电耦合系数k2也可分成4个范围进行分析:

1) 当hLN=0.01λ～0.1λ时,k2先增加,在hLN=0.05λ处达到极大值后逐渐减小至0。当hLN= 0.01λ～0.05λ时,随着hLN增加,能量转换效率提高,所以k2增加。当hLN= 0.06λ～0.1λ时,因为表面波逐渐与体波耦合,所以k2反而减小。同时可见,在该范围内,因为hLN很小,能量转换效率低,所以k2的极大值小于0.3%。

2) 当hLN=0.1λ～0.8λ时,因为无法激发瑞利波模式,所以此范围无k2的计算结果。

3) 当hLN=0.8λ～1.2λ时,对应于图3中所给模式,其k2值从0.29%增加到5.28%,这与图3中该hLN范围内表面波能量随hLN增大而逐渐增加,体波能量逐渐减小的分析结果一致。

4) 当hLN>1.2λ时,因已激发出了稳定的瑞利波模式,故k2从5.28%增加至5.56%,上升趋势趋于平缓,且接近单晶LN的k2值(约为5.5%)[20]。

2.2 PI厚度对SAW器件的影响

当PI厚度很小(小于λ)时,此时声速、机电耦合系数与PI厚度的关系及振型图如图5所示。研究中假设LN和BCB的厚度分别为0.06λ和0.1λ。由图可看出,当PI厚度从0.3λ增加到λ时,其声速从985 m/s降低到800 m/s,而k2基本保持不变。这是由于随着PI衬底厚度增加,更多的声波能量进入PI中传播,导致声速下降。

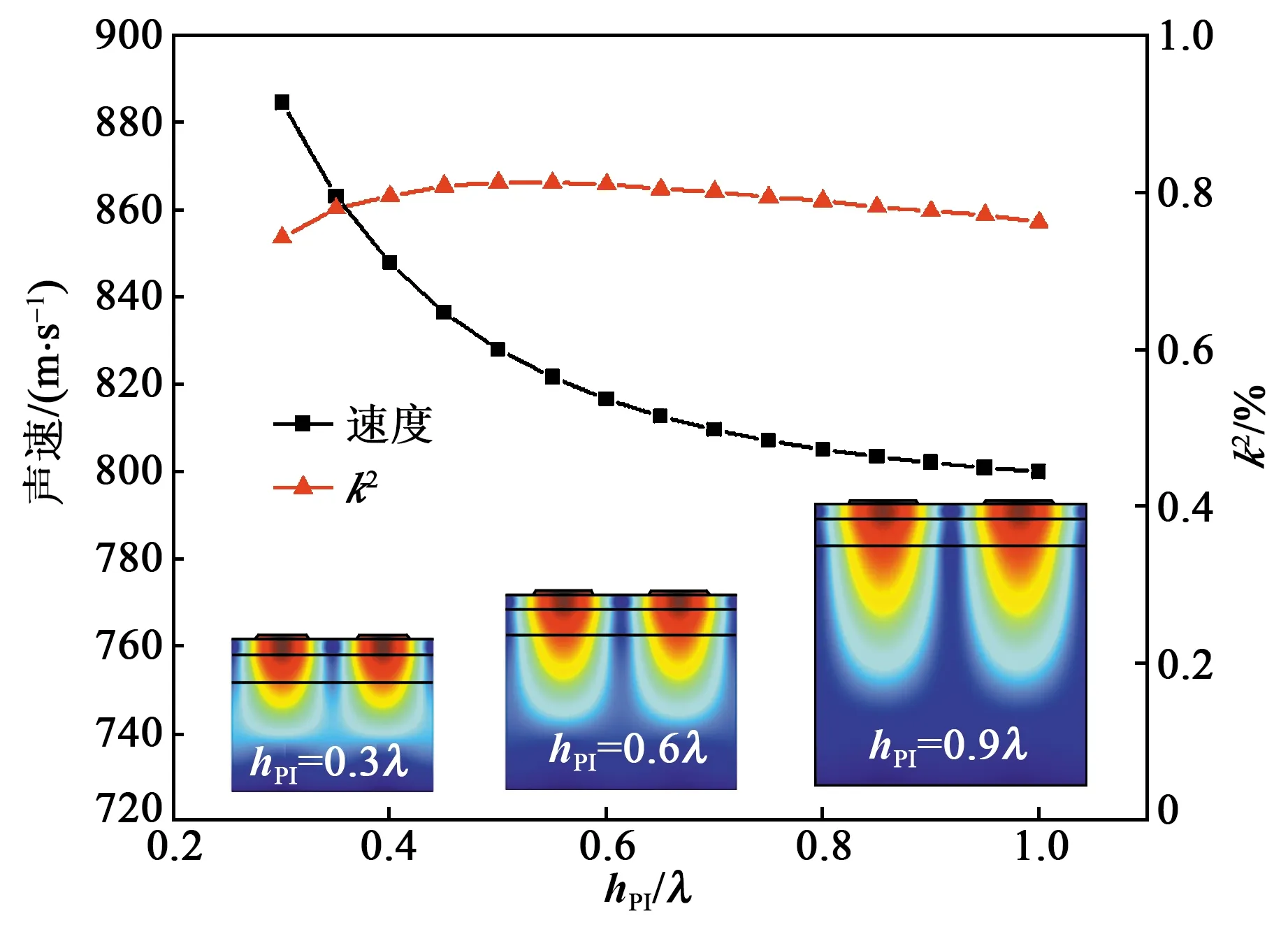
图5 PI厚度对声速和机电耦合系数的影响

2.3 温度对SAW器件谐振频率的影响

图6为器件谐振频率随温度的变化关系。在此研究中,LN和BCB的厚度分别为0.06λ和0.1λ。由图可看出,随着温度升高,器件的谐振频率降低。

SAW器件的谐振频率将受到温度的影响。谐振型SAW传感器的谐振频率为

(6)

式中v为压电衬底的声速。SAW器件的频率温度系数(τf)为

uf-α

(7)

由式(7)可以看出,影响τf的两个主要因素是材料的声速温度系数uf和线性热膨胀系数α。图6同时给出了热膨胀系数及声速温度系数引起的谐振频率变化。由图6可看出,与热膨胀系数相比,声速温度系数对谐振频率变化的影响较大。因此,在研究器件的温度特性时,重点考虑器件的声速温度系数的影响。

由图6还可发现,该器件的τf约为906×10-6/℃,大于通常LN器件的τf[20]。这是由于当温度从25 ℃升到200 ℃时,LN的表面波声速从3 823 m/s降低到3 769 m/s(相对变化为-1.41%),而PI中的表面波声速从760 m/s降低到603 m/s(相对变化为-20.7%,这是由于 PI作为高聚物,其弹性模量随温度变化很大),可见PI中声速温度系数大于LN声速温度系数。在该仿真结构中,LN厚度仅0.06λ,声波主要在PI中传播,导致该器件的τf主要受PI的影响,所以其τf比LN单晶块材SAW器件的τf大。另一方面,如果需要降低该器件的τf,通过掺杂调控PI的弹性模量可使其力学性能随温度敏感性降低[21]。

3 结束语

本文针对“LN/BCB/PI”结构的SAW器件研究了LN、 BCB和PI厚度对器件特性的影响,同时还研究了当温度变化时器件的谐振频率变化。结果表明,LN厚度为0.06λ～0.8λ时,不能激发瑞利波模式。当LN厚度为0.01λ～0.06λ或大于1.2λ时,可以激发稳定的瑞利波模式。当LN厚度为0.8λ～1.2λ时,虽然可激发瑞利波模式,但表面波会与体波耦合。LN厚度为0.01λ～0.06λ时,瑞利波的机电耦合系数先增加后减小。LN厚度为0.8λ～1.5λ时,机电耦合系数逐渐增加并趋于单晶LN的机电耦合系数值。当温度升高时,器件的谐振频率降低,这主要是由于声速随温度变化引起的。本文的仿真结果为设计基于LN薄膜的柔性SAW传感器时合理选择压电薄膜厚度及衬底材料的力学性能等参数提供了一定的理论依据。