单轴MEMS热膨胀流陀螺敏感机理三维有限元分析
2023-05-31朴林华佟嘉程
朴林华,李 备,佟嘉程,张 严
(北京信息科技大学 北京市传感器重点实验室,北京 100192)
0 引言
热膨胀流陀螺仪是一种新颖的角速度惯性传感器,其原理是利用加热器产生的热膨胀流在哥氏力作用下发生偏转而引起的不平衡热效应工作[1]。与传统的微机械振动陀螺仪相比,其最大的特点是不含固体质量块,敏感质量为气体,且具有抗冲击能力强,结构简单,质量小及可靠性高等优点,可应用于导航、汽车电子、无人机、可穿戴电子设备等领域[2-3]。2012年,Leung教授首次提出了热膨胀流陀螺的结构和敏感机理,该结构含有两个加热器和一对温度传感器,通过两个加热器交替加热产生“推拉式”的热膨胀流,通过热敏电阻来检测由科氏力引起的温度差,从而检测z轴角速度[4]。2013年,朱荣等提出了一种基于热膨胀的微加工气体惯性传感器[5],该传感器由3个交替加热的加热器和4个热敏电阻组成,3个加热器悬浮在蚀刻有密闭腔室的硅衬底上,4个热敏电阻对称地悬浮在两个相邻的加热器之间,它可实现单轴加速度和单轴角速度的测量。2015年,文献[6]提出了一种基于热膨胀流的微机械流体惯性传感器,它可以实现单轴(z轴)角速度和双轴(x轴和y轴)加速度的同时检测。然而,这些热膨胀流陀螺的加热器与热敏电阻垂直,加热器加热时会使长度方向的气体热膨胀流增加,宽度方向的热膨胀流减小,这将导致加热器产生的部分热气流损失到相邻边界,造成其加热效率不高[7],灵敏度较低。同时,目前的热膨胀流陀螺均采用二维模型进行陀螺性能的预测和敏感机理的验证,但二维模型与真实情况相差甚远,计算结果存在极大误差。因此,本文提出了一种单轴微机电系统(MEMS)热膨胀流陀螺结构,通过加热器与热敏电阻平行的设计增加宽度方向的热膨胀流,使更多的热膨胀流流向热敏电阻,从而提高加热效率,提升热敏电阻之间的温差,达到提高灵敏度的目的。为了降低传感器的制作成本,缩短研发周期,提高传感器的性能,在制作流片之前需要对传感器的敏感机理及影响传感器性能的诸因素进行大量的理论研究[8]。本文利用COMSOL Multiphysics软件对MEMS热膨胀流陀螺建立三维模型,利用有限元法对温度场和等温线的变化情况进行计算,研究该新型结构陀螺的敏感机理,为该陀螺后续的结构改进、性能优化奠定理论基础。
1 结构原理
单轴MEMS热膨胀流陀螺仪由热敏元件和上盖组成,其三维结构如图1、2所示。
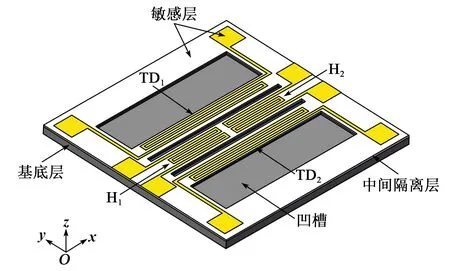
图1 单轴MEMS热膨胀流陀螺仪的热敏元件三维结构示意图

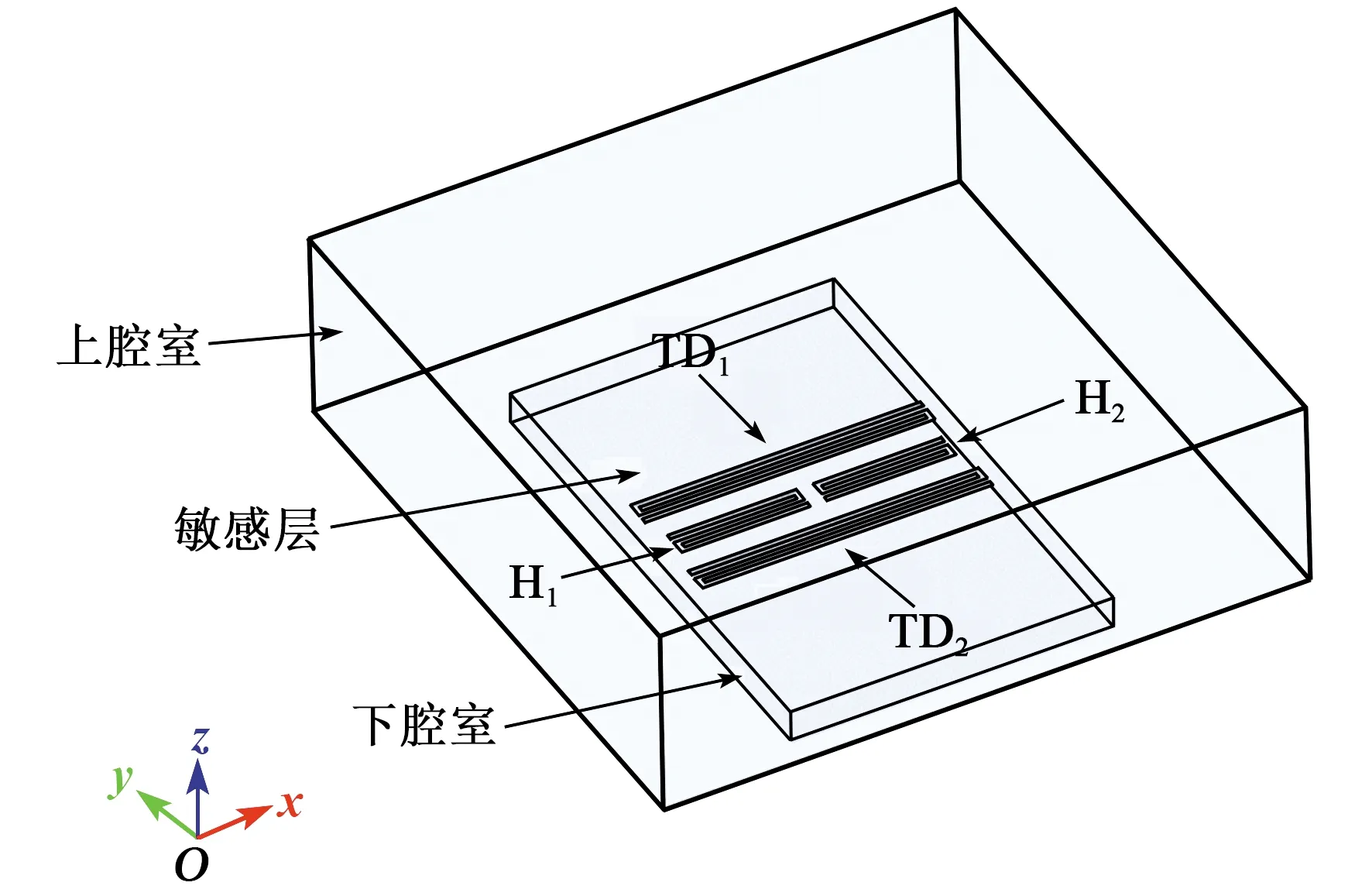
图2 单轴MEMS热膨胀流陀螺仪的上盖三维结构示意图
热敏元件包括敏感层、中间隔离层和基底层。其中,敏感层含有两个对称分布的加热器(H1、H2)和一对平行的热敏电阻(TD1、TD2),加热器和热敏电阻均由同一温度系数的铂材料构成,并通过溅射工艺制作。基底层的主要材料是单晶硅,中间隔离层的主要材料是二氧化硅。基底层和中间隔离层通过湿法刻蚀工艺刻蚀有4个矩形的凹槽(下腔室),该凹槽(下腔室)和上盖的空腔(上腔室)共同构成热气体的工作空间。
图3为热膨胀流陀螺的工作原理示意图。两个加热器(H1、H2)通过周期性的方波信号交替加热,加热器周围的气体体积受热膨胀,产生“推挽式”的热膨胀流。两个热敏电阻(TD1、TD2)阻值相同,可敏感热气体的温度变化。假设热敏电阻TD1、TD2敏感到的温度分别为T1、T2,则两热敏电阻间的温度差:

图3 单轴MEMS热膨胀流陀螺仪的工作原理示意图
ΔT=T1-T2
(1)
当z轴无角速度时,H1通电加热,其周围气体受热膨胀,H2周围的气体冷却收缩,热流由H1流向H2,如图3(a)所示;H2通电加热时,其周围气体受热膨胀,H1周围的气体冷却收缩,热流由H2流向H1,如图3(b)所示。此时热敏电阻的温度相同,温度差ΔT=0。当z轴存在角速度输入时,H1通电加热,设H1产生的热膨胀流的质量为m,流速为vf,角速度为ωz,热膨胀流受到哥氏力FC的作用,有:
FC=2mvf×ωz
(2)
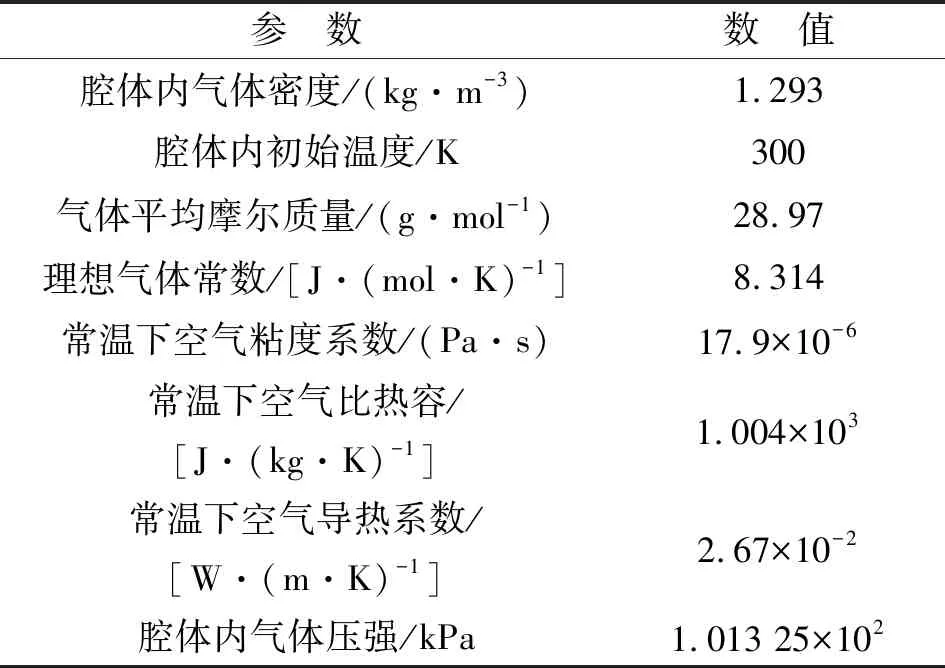
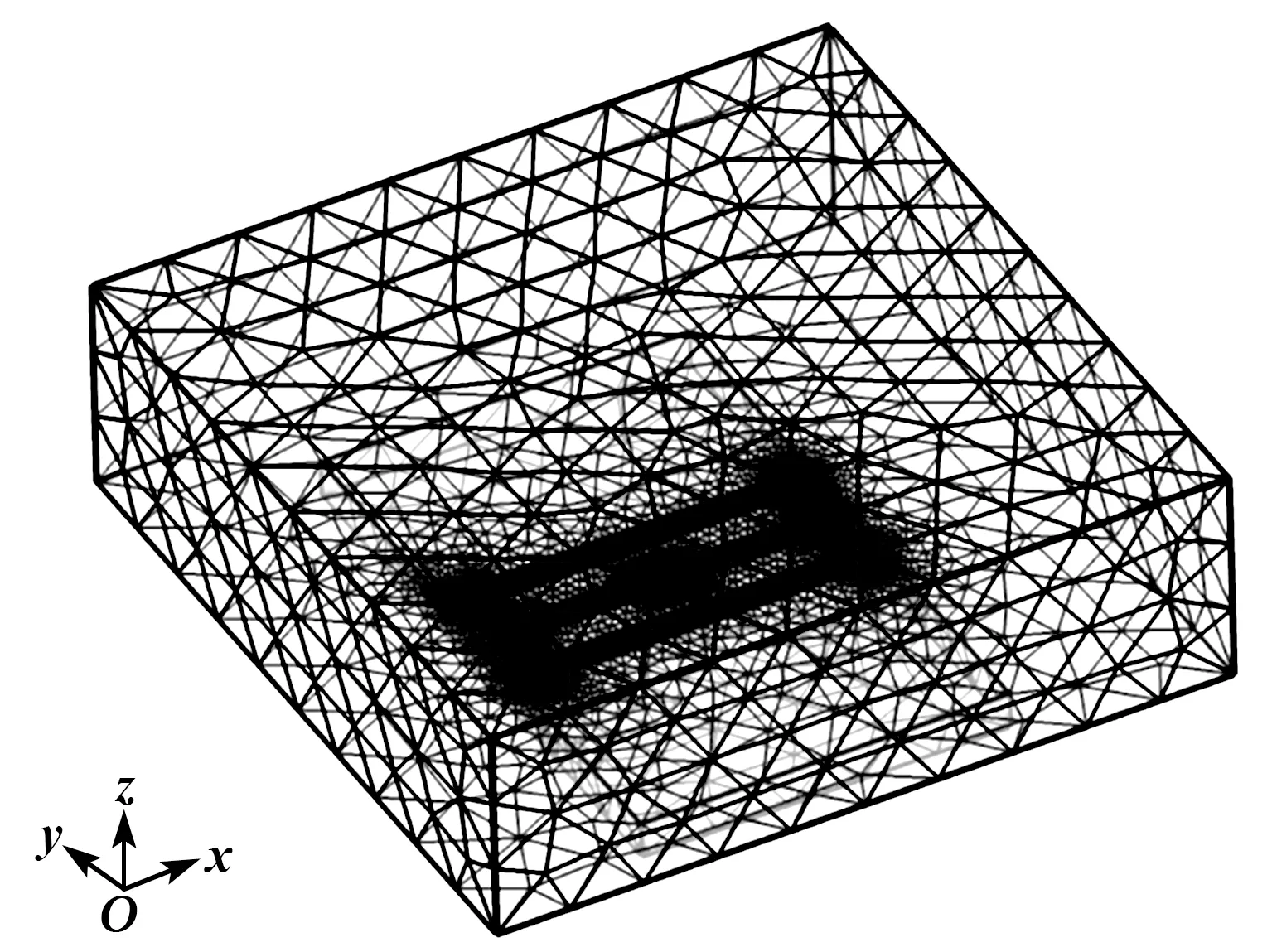
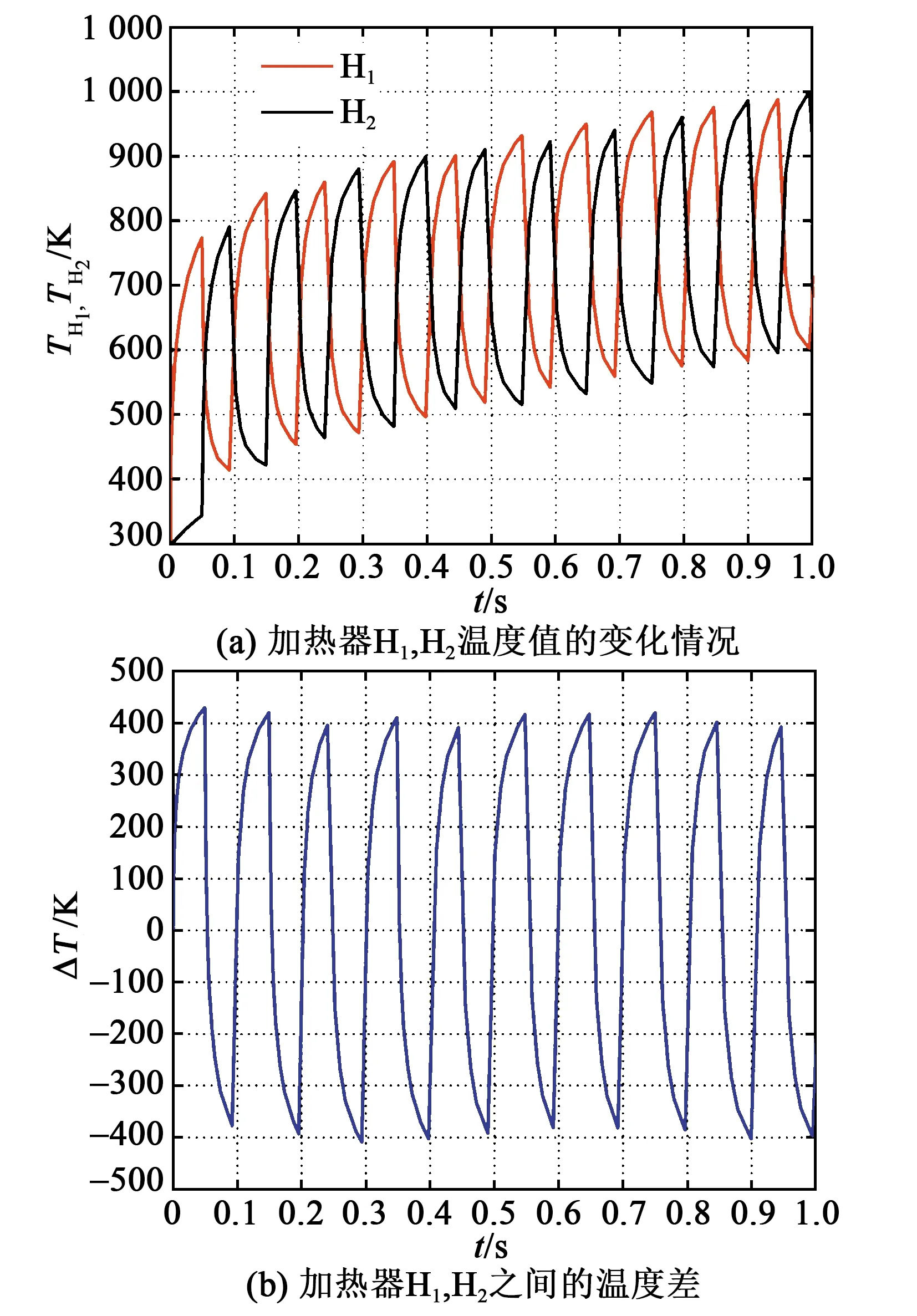
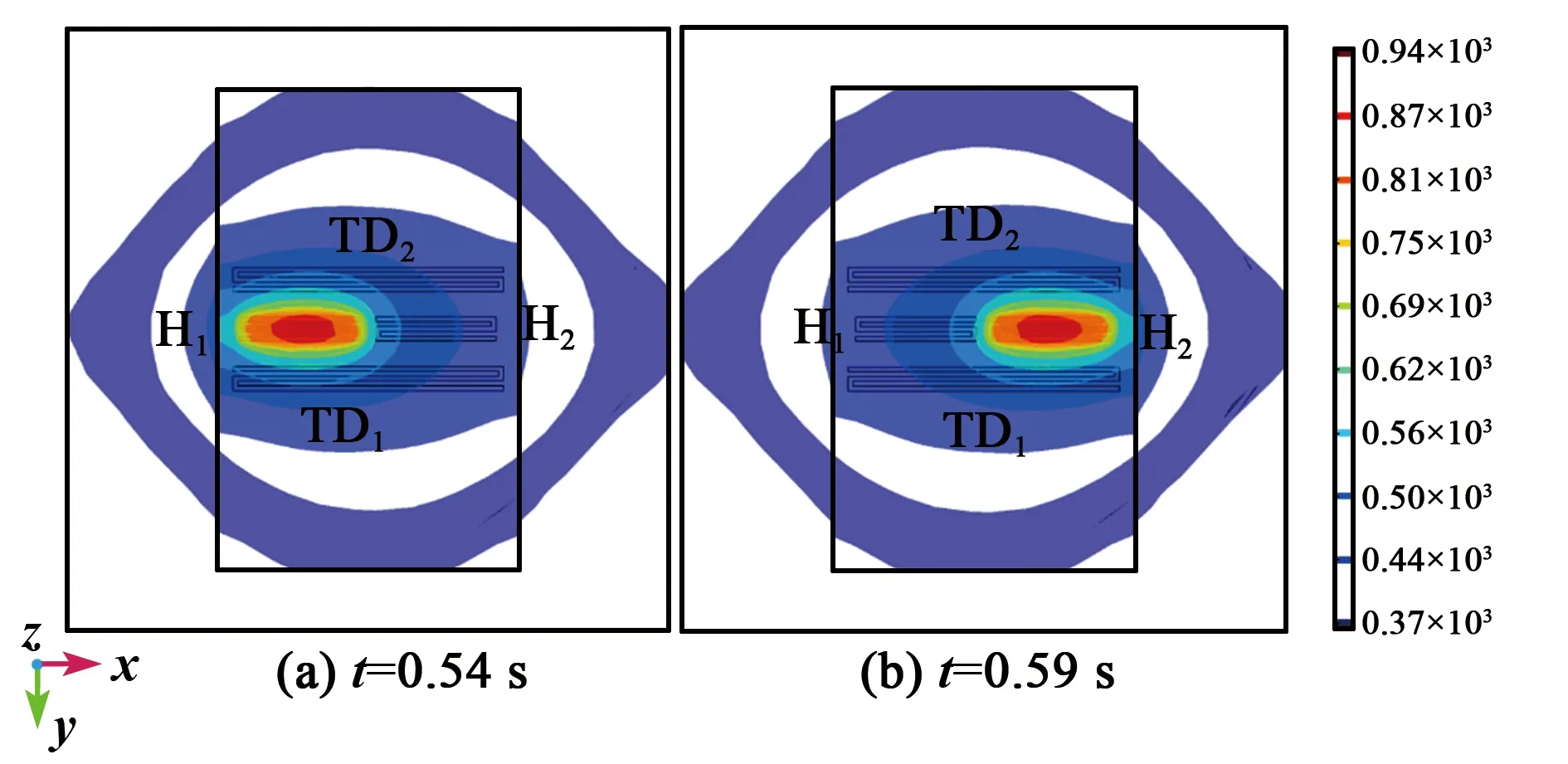
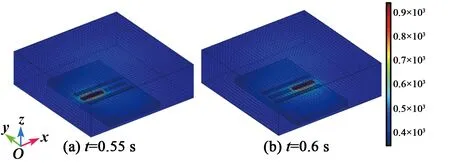
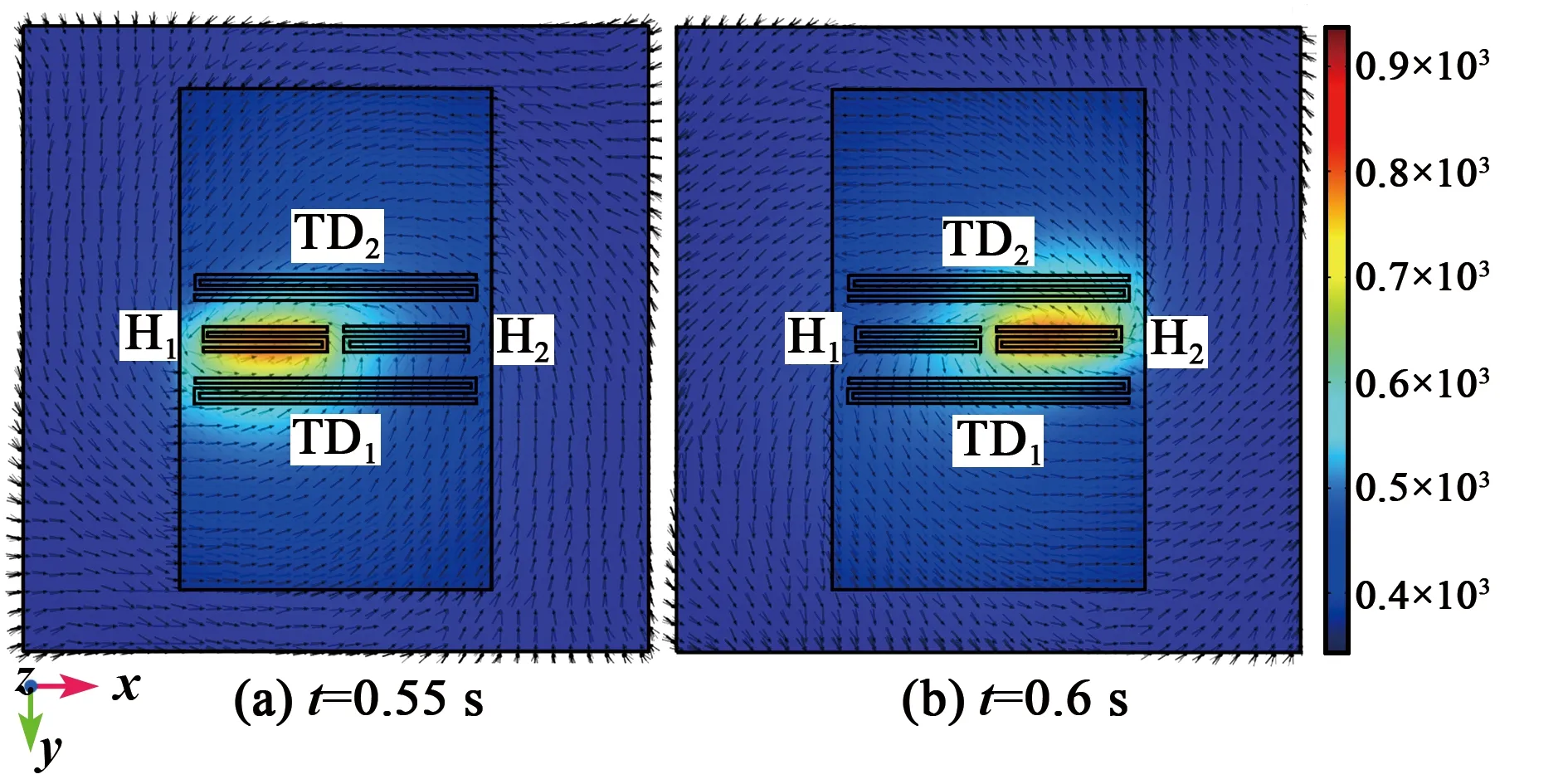
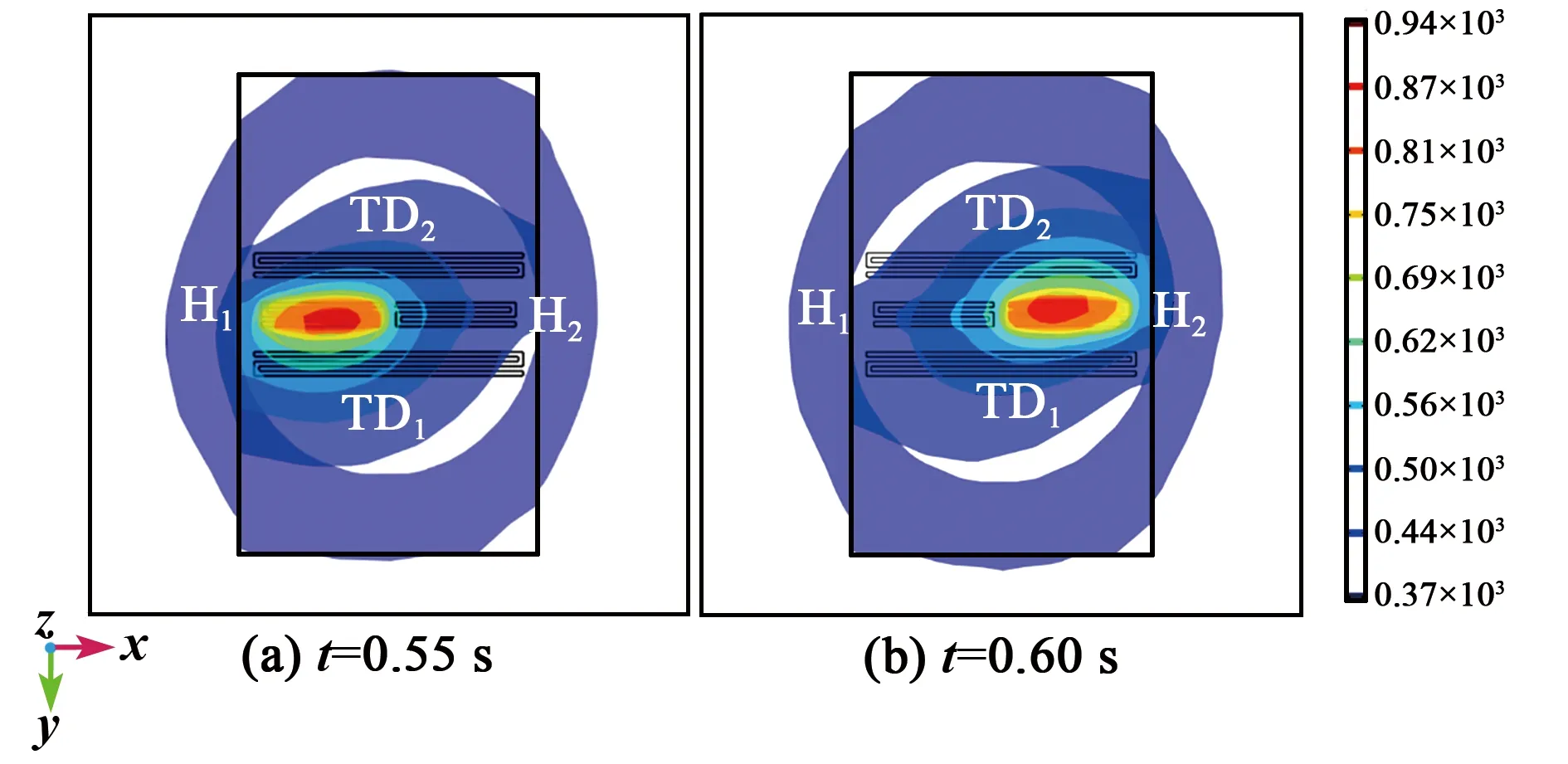
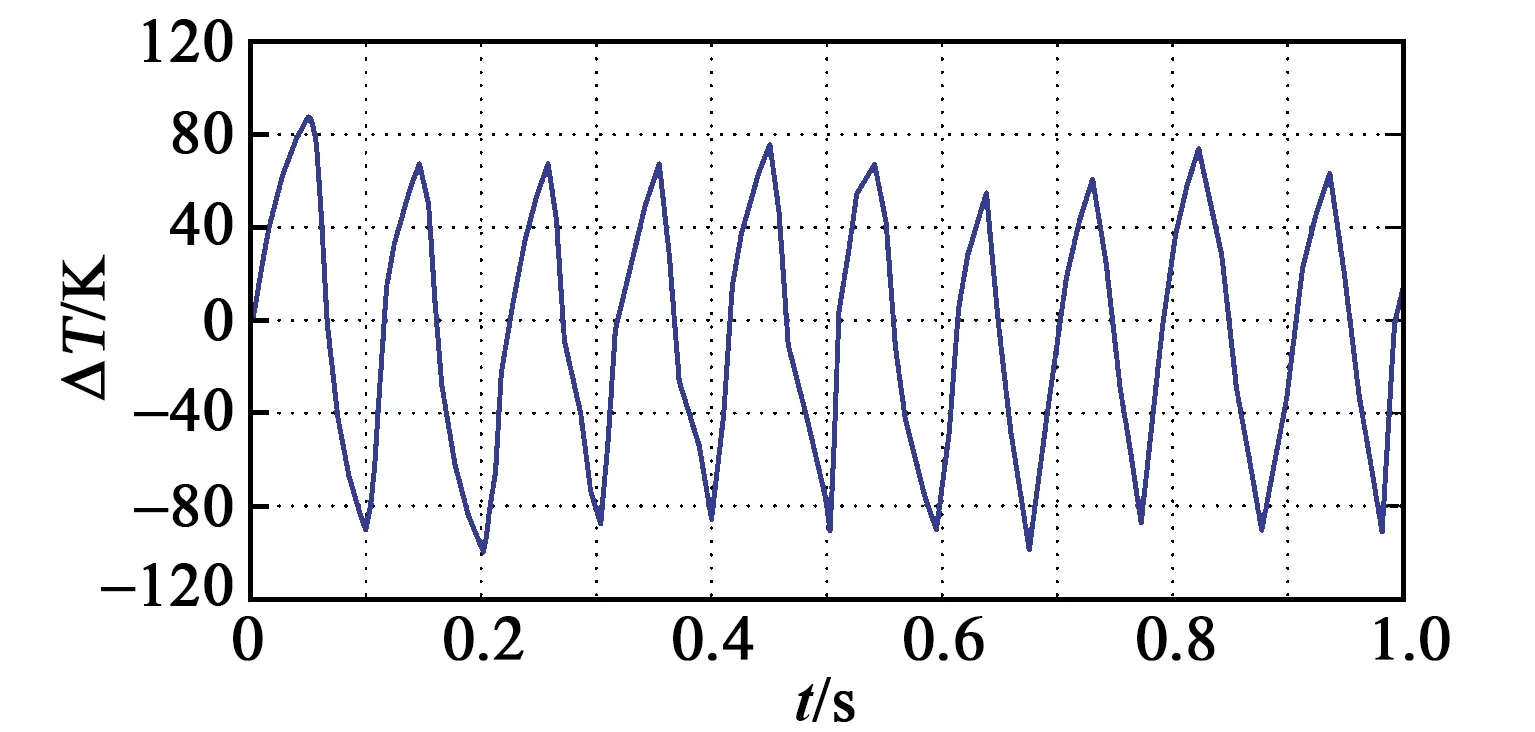
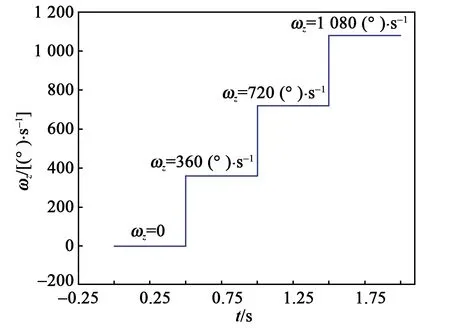
根据右手定则,FC方向为y轴正方向,此时H1产生的热膨胀流向上偏转,如图3(c)红色箭头所示,热敏电阻TD1周围温度升高,T1>T2,ΔT>0。当H2通电加热时,在哥氏力FC作用下,热气体会破坏原有的路径而向相反方向偏转,热膨胀流对称地流向TD2,如图3(d)所示,此时热敏电阻TD2周围的温度升高,T1 金属Pt电阻与温度的关系为 RT=R0(1+AT+BT2) (3) 式中:RT表示温度为T时铂电阻阻值;R0表示温度为0时铂电阻阻值;A为铂电阻的温度系数;B为非线性系数。由于低温时B很小,故设B近似为0,所用热敏电阻均为线性,A为常数,则: RTD1=R0(1+AT1) (4) RTD2=R0(1+AT2) (5) ΔR=RTD1-RTD2=AR0(T1-T2)= AR0ΔT (6) 式中:ΔR为热敏电阻的阻值变化;RTD1、RTD2分别为热敏电阻TD1、TD2阻值。根据Pt薄膜电阻的特性,热敏电阻可将温度差转化为热敏电阻间的阻值差。 如图4所示,将热敏电阻TD1、TD2接入惠斯通电桥的两个桥臂,可进一步转化为电压差。 图4 惠斯通电桥结构示意图 此时电桥输出可表示为 (7) 式中:α为差分放大器的放大倍数;R1、R2为参考电阻,且R1=R2,由于TD1和TD2为同一温度系数的金属Pt电阻,故RTD1=RTD2。将R1=R2、RTD1=RTD2及式(4)~(6)代入式(7)可得到: (8) 由式(8)可见,MEMS热膨胀流陀螺仪的输出电压与ΔT成正比,即Vout∝ΔT,又因ΔT∝ωz,故ωz∝ΔT∝Vout。通过检测电压的变化可实现z轴角速度的测量。 MEMS热膨胀流陀螺的三维物理模型如图5所示。图中,下腔室对应基底和隔离层的凹槽,上腔室对应上盖的空腔,腔室内填充空气。模型仅考虑气体在两个加热器H1、H2交替加热作用下,热敏电阻TD1、TD2的温度场和等温线的变化情况。忽略加热器和热敏电阻的结构对气体温度场和等温线的影响,即其结构不会对气体的流动及温度分布产生阻碍。 图5 单轴MEMS热膨胀流陀螺结构的三维模型 施加在加热器上的周期性方波信号可以通过软件自带的方波函数和解析函数组合得到[8]。设置两个不同的方波函数r1(t)、r2(t),参数区间分别设置为 (0,0.05)、(-0.05,0),绘制两个方波函数。通过定义函数h1(t)=0.07r1(t)、h2(t)=0.07r2(t),将方波函数r1(t)和r2(t)进行周期性扩展,设h1(t)的区间为(0,0.1),设h2(t)的区间为(-0.1,0),变元t的区间均为(0,2),最终得到如图6所示的周期性方波函数。三维COMSOL模型尺寸如表1所示。 表1 MEMS热膨胀流陀螺COMSOL模型尺寸 图6 加热器驱动信号 MEMS热膨胀流陀螺腔体内部的气体流动和温度变化过程符合质量守恒方程、惯量守恒方程、热能守恒方程和状态方程[1]: (9) (10) (11) P=ρRT (12) 式中:ρ为气体密度;u为气体的速度矢量;μ为气体的粘度系数;cp为气体的比热容;T为气体温度;K为导热系数;P为压强;R为理想气体常数[9]。将空气作为腔体内部的工作气体,其相关参数如表2所示。 表2 三维COMSOL模型工作气体的相关参数 在确立物理模型和数学模型后,利用COMSOL软件对陀螺的敏感元件在有无角速度时温度场的变化情况进行有限元分析和计算。其求解过程如下: 1) 建立有限元模型(见图5)。由于加热器加载的驱动信号为周期性变化的方波信号,所以设置研究类型为瞬态。 2) 模型参数设置。对于敏感元件部分,设置加热器和热敏电阻的材料、密度、导热系数及定压比热。对于腔体部分,设置工作气体的密度、比热容及导热系数,同时还需设置加热器驱动信号的占空比、频率和幅值。此时角速度沿z轴方向输入,且ωz=1 080 (°)/s。 3) 物理场选择。在敏感元件腔体内部,加热器加热引起温度场的变化,包含热传导、热对流等物理过程,故选择共轭层流物理场,其中包括固体和流体传热、层流两个物理场。同时,系统在多物理场中自动生成非等温流动物理场。计算过程中发现,使用层流物理场计算三维模型需要几天时间,且对计算机内存要求极高,为简化计算,本模型仅采用固体和流体传热物理场。 4) 划分网格。有限元分析的精度与所用的网格密切相关,因此,网格划分的质量对计算精度、计算时间、收敛性均有影响,并对计算机内存及计算能力有较高的要求。为了节省计算时间,网格的单元尺寸设为常规,网格划分结构如图7所示。 图7 三维模型的网格划分 5) 计算。定义瞬态研究的计算时间为2 s,步长为0.01 s,然后进行计算。 由于加热器的加热功率为70 mW,交替加热的时间为0.05 s,因此,加热器H1、H2的温度TH1、TH2呈现周期性“推挽式”的交替变化,如图8(a)所示。随着时间的增加,加热器的最高温度不断升高,但两个加热器之间的温度差趋于稳定,平均温度差约为400 K。两个加热器之间的温度差变化曲线如图8(b)所示。在无角速度输入时,温度场和等温线的计算结果如图9~11所示。由图11可见,当t=0.59 s时,加热器H2加热,H1冷却,热膨胀流由H2对称地流向TD1、TD2。根据计算结果分析可知,在无输入角速度的条件下,加热器交替加热产生的热膨胀流对称地流向热敏电阻,两热敏电阻感受到的热气体位于同一等温线上,其温度分布对称,故其温度变化相同,即ΔT=0。 图8 加热器的温度变化情况曲线图 图9 无角速度、H1、H2加热时陀螺温度场的运动情况 图11 无角速度、H1、H2加热时陀螺等温线的分布情况(顶视图) 图12是ωz=1 080 (°)/s时加热器与热敏电阻温度值的变化情况对比图。由图可知,热敏电阻的温度改变滞后于加热器的温度改变,且滞后时间的平均值为Δt=0.014 s。因此,在观察热敏电阻的温度变化时,选取t=0.55 s和t=0.6 s时的情况进行说明。 图12 ωz=1 080 (°)/s时加热器与热敏电阻温度值的变化情况对比图 在输入角速度ωz=1 080 (°)/s时,温度场和等温线的计算结果如图13~15所示。为了更好地说明热气体温度场的运动情况,将面上箭头的位置设置为“均匀各向异性”,并增加了图13、14中面上箭头的个数。 图13 ωz=1 080 (°)/s、H1、H2加热时陀螺温度场的运动情况 图14 ωz=1 080 (°)/s、H1、H2加热时陀螺温度场的运动情况(顶视图) 图15 ωz=1 080 (°)/s、H1、H2加热时陀螺等温线的分布情况(顶视图) 由图13~15可以看出,在t=0.55 s时,加热器H1加热,H2冷却,加热器加热产生的热膨胀流在哥氏力作用下发生偏转,由于陀螺旋转方向为顺时针,故加热器H1产生的热膨胀流更多地流向热敏电阻TD1,使TD1周围气体的温度大于TD2周围气体的温度(T1=737.92 K,T2=664.99 K),故ΔT=72.93 K;同理,在t=0.6 s时,加热器H2加热,H1冷却,加热器加热产生的热膨胀流在哥氏力作用下发生偏转,由于陀螺旋转方向为顺时针,故加热器H2产生的热膨胀流更多地流向热敏电阻TD2,使TD2周围气体的温度大于TD1周围气体的温度(T1=666.21 K,T2=753.65 K),故ΔT=-87.44 K。该结论验证了MEMS热膨胀流陀螺仪的敏感机理,是灵敏度计算的基础。 随着加热器的交替加热,热敏电阻的温度差也呈现交替变化。图16为ωz=1 080 (°)/s时热敏电阻间的温度差随时间变化的关系。加热器H1加热时,热敏电阻的最大温差为87.67 K;加热器H2加热时,热敏电阻的最大温差为99.74 K。 图16 ωz=1 080 (°)/s时,热敏电阻间的温度差随时间变化的关系 为了进一步验证MEMS热膨胀流陀螺的陀螺效应,需要对三维模型产生的与灵敏度有关的信号进行分析和整合[10-11]。通过将恒定角速度改为一般角速度,大小设置为pw1(t)。其中,pw1为图17所示的分段函数,时间每增加0.5 s,角速度增加360 (°)/s。 图17 ωz=pw1(t)时,分段函数pw1的波形图 通过COMSOL数值模拟得到热敏电阻在不同角速度下的温度差ΔTD=T2-T1,如图18所示。图18(a)为COMSOL全局变量探针输出的结果,说明热敏电阻在不同转速下的ΔTD随着加热器每半个加热周期的变化而变化,且其温度差的大小随角速度增大而增大。图18(b)为图18(a)整流后的结果,说明加热器交替加热时,每半个周期的输出信号幅值存在差异,这将直接导致每半个周期的输出电压的幅值存在差异。 改变输入角速度的大小,通过COMSOL数值计算得到输入角速度与热敏电阻的温度差ΔT的关系如图19所示。由图可知,ΔT∝ωz。通过最小二乘法拟合得到MEMS热膨胀流陀螺的结构灵敏度为0.053 9 K/[(°)/s-1],非线性度为14.13%。这说明MEMS热膨胀流陀螺存在陀螺效应,是后续探究陀螺灵敏度影响因素及模型优化的基础。 图19 热敏电阻的温度差ΔT与输入角速度ωz的关系 本文提出了一种单轴热膨胀流陀螺仪,并介绍了其结构和原理。在角速度变化时,加热器产生的热膨胀流在哥氏力作用下发生偏转,进而引起与之平行的热敏电阻的温度变化,将温度变化转化为输出电压的变化,从而实现z轴角速度的精确测量。同时,利用COMSOL Multiphysics建立了三维模型,对陀螺的敏感机理进行有限元分析,得到其腔室内气体在无角速度和有角速度时温度场和等温线的运动情况。结果表明,单轴MEMS热膨胀流陀螺具有陀螺效应,输入角速度在[-1 080 (°)/s,1 080 (°)/s],陀螺的结构灵敏度为0.053 9 K/[(°)/s-1],非线性度为14.13%。与现有的微型热气体陀螺仪相比,该陀螺具有抗冲击能力强、结构简单、成本低、功耗低[12]等优点,可应用于导弹[13]、微小型地面机器人[14]、微型飞行器[15]等领域。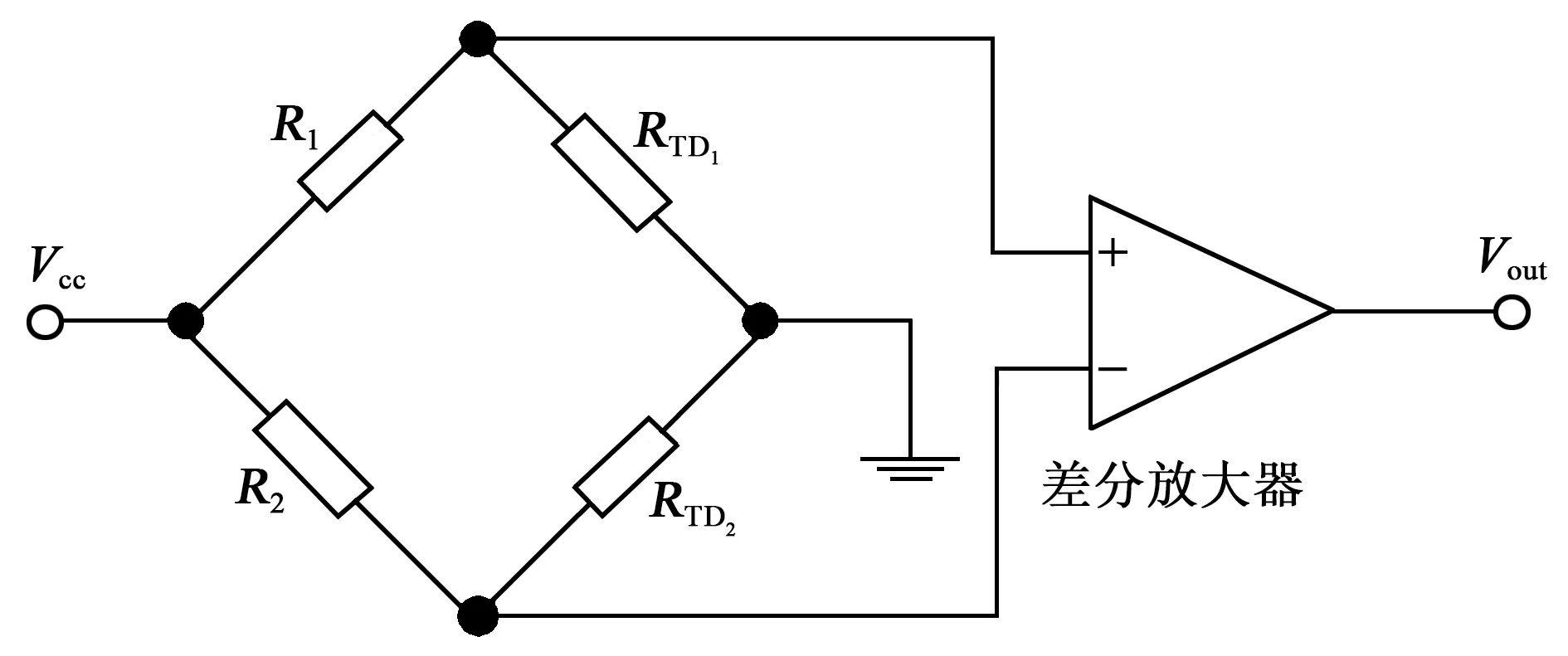
2 有限元计算
2.1 物理模型


2.2 数学模型

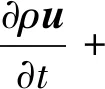
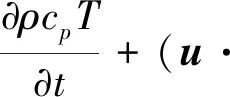
2.3 有限元法求解
3 计算结果及讨论



4 结束语
