检测误差对半球谐振陀螺进动因子的影响分析

韩世川,林翠平,陈婷婷,雷 霆,卜继军

(1.中国电子科技集团公司 第二十六研究所,重庆 400060;2.固态惯性技术重庆市工程实验室,重庆 401332;3.重庆市固态惯性技术企业工程技术研究中心, 重庆 401332)

0 引言

半球谐振陀螺(HRG)是基于哥氏效应的振动陀螺,通过检测谐振子振型的变化来测量载体的角速率和角度。当一个振动的轴对称壳体绕其对称中心轴旋转时,环向振型相对壳体呈比例进动,这种现象称为布莱恩(Bryan)效应。

工作于全角模式的半球陀螺,激励谐振子处于四波腹驻波振动状态,当外界载体带动陀螺基座旋转时,受哥式力的作用,驻波角位置相对于基座将发生进动。通过检测驻波进动角度实现载体转动角度的测量,驻波进动角度与外界载体转动角度之比称为进动因子α,α仅与谐振子物理形状相关。实际工作中,半球谐振陀螺由于电极间隙误差、电路增益误差及电极非正交耦合误差等检测误差的存在,将导致进动因子的周向一致性退化。电极间隙误差与前级电路增益误差统称为增益误差,电极非正交耦合误差统称为耦合误差。本文通过理论推导了增益误差和耦合误差对进动因子的影响,并提出了校正这两类误差的方法,通过实验结果证明了该方法的有效性。

1 理想半球陀螺进动因子推导

理想半球谐振子以基尔霍夫-李雅夫假设为基础[1-2],建立理想谐振子壳体动力学模型,即谐振子的密度、厚度、半径、弹性模量和泊松比都是常数,与圆周角无关,求解薄壳表面任意质点的运动方程。

如图1所示(图中θ,β,R为球形坐标),半球谐振子以角速度Ω绕对称轴旋转,R为谐振子曲面上任一质点A的中曲面半径,假设谐振子壁厚均匀不变,只有沿对称轴z轴有输入角速度,即Ωx=Ωy=0。

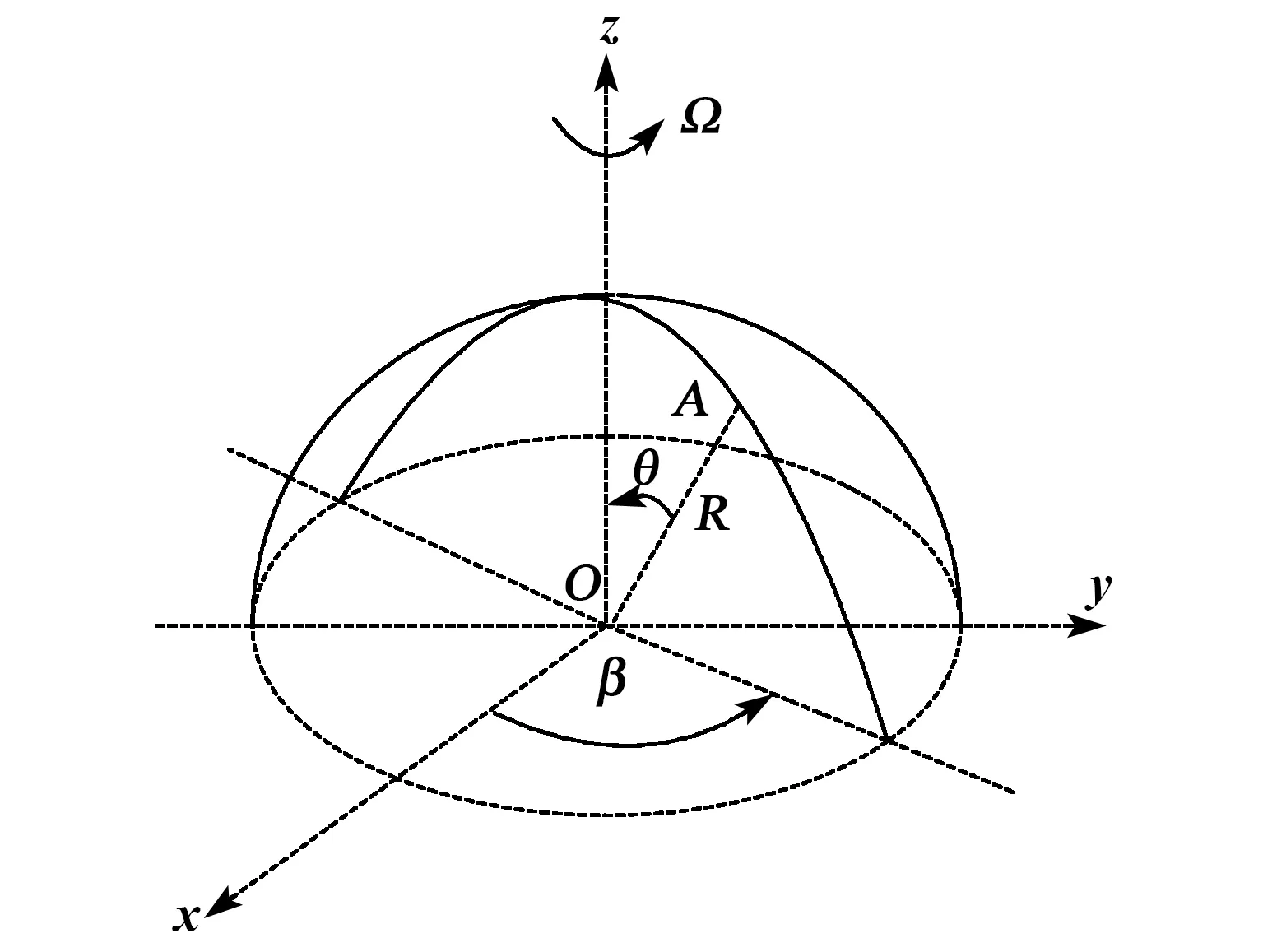
图1 薄壳谐振子球面坐标示意图

对于理想系统,内力和科里奥利力均不做功,系统能量保持不变,利用布勃诺夫-伽辽金法对理想半球谐振子的任意质点运动方程进行求解,得到理想谐振子二阶固有振型的动力学方程为

(1)

式中:m0为等效质量;p1(t)、p2(t)是谐振子质点位移在Ln[cos(nβ),sin(nβ)]空间的正交分解;c0为等效刚度;b为等效阻尼。且:

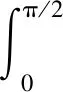
(2)

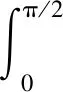
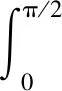
(3)

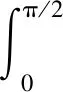
(4)

(5)

式中U(θ),W(θ)为不可拉伸薄壳n阶固有振型的瑞利函数。

式(1)是一个典型的二阶弹性系统运动方程,忽略了外力和系统阻尼的存在,且认为弹性系统完全对称,其动力学方程为

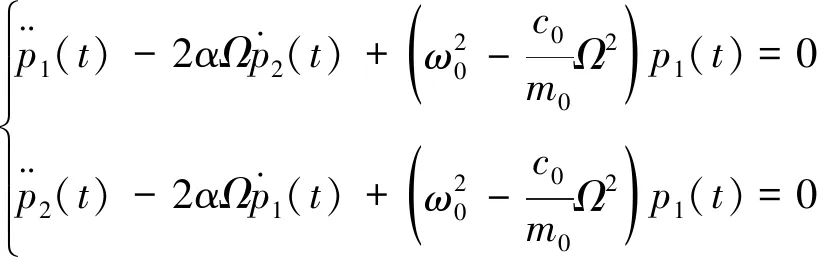
(6)

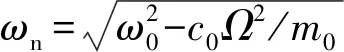
根据式(2)、(4)可得到陀螺进动因子的理论式为

0.277

(7)

式(1)、(7)是针对理想型谐振子,其进动因子仅与球壳形状有关,当谐振子材料为熔融石英玻璃材料时,具有很好的稳定性,可用驻波的进动信息得到外界载体的角速率。

2 全角模式下进动因子的影响因素

为方便计算,可将半球陀螺的振动方程表示为向量形式,不考虑阻尼和频差的周向不均匀,即:

(8)

(9)

(10)

式(8)的解可表示为

(11)

式中:a(t)为主振动幅度;q(t)为正交振动的幅值;θ(t)为主振动波腹与p1方向的夹角,即驻波方位角。

将式(11)代入式(8)可得:

(12)

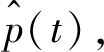
(13)

式中A为2×2的增益矩阵[3]。检测误差包括增益误差和耦合误差,分别对应矩阵Ad和矩阵Ae,则矩阵A可表示为两者的乘积:

(14)

式中:a11,a22分别为x、y轴的检测增益误差;a12、a21为x、y轴检测信号间的通道耦合误差。

将式13代入式(8)有:

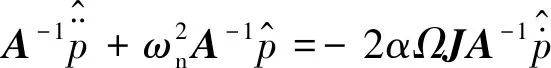
(15)

陀螺实际工作过程中,a为主振动幅度,正交振动通过施加与主振动相位一致的正交控制力得到了有效的抑制,q=0,陀螺的振动位移可表示为

p(t)=av(t)cos(ωnt)

(16)

将式(16)代入式(15)可得:

(17)

(18)

通过式(17)、(18)可知,进动因子随驻波方位角的变化将会影响半球陀螺的性能,同时也会造成幅度、正交控制施力的角度误差。

3 全角模式控制电路与算法

基于现场可编程门阵列(FPGA)+数字信号处理(DSP)+模数转换器(ADC)+数模转换器(DAC)全角模式控制电路[5]主要包括缓冲放大电路、两路模数转换器(ADC)采样、输入解调、数字滤波、数字直接数字频率合成器(DDS)、输出调制、两路数模转换器(DAC)控制等功能模块,其功能模块如图2所示。

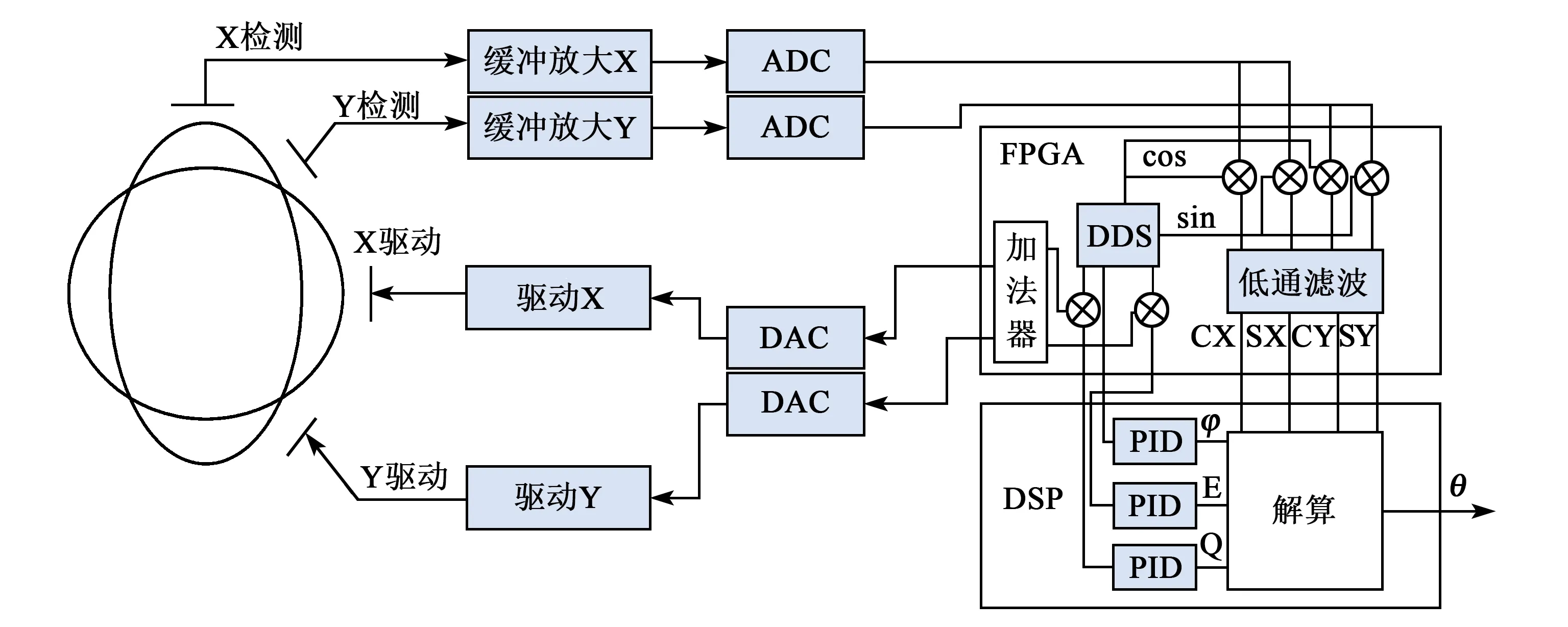
图2 全角模式控制电路框图

根据Lynch给出的广义振动陀螺模型[6]可知,理想振动陀螺无外部输入时,90°和45°电极作为检测电极,探测到的信号分别表示为

x=acos(2θ)cos(ωτ+φ′)-

qsin(2θ)sin(ωτ+φ′)

(19)

y=asin(2θ)cos(ωτ+φ′)+

qcos(2θ)sin(ωτ+φ′)

(20)

式中:a为陀螺的主振动幅度;q为陀螺的正交振动幅度;ω为陀螺振动频率;φ′为振动的初始相位。

通过在FPGA内部生成DDS,跟踪陀螺的振动频率与相位构成数字锁相环,设DDS信号幅值为A,则DDS的输出为

vrc=Acos(ωτ+φ)

(21)

vrs=Asin(ωτ+φ)

(22)

同时用作输入解调和输出调制信号[4]。通过在FPGA内部IQ解调,然后进行数字滤波得到cx、cy、sx、sy,δφ为陀螺初始相位φ′与本地同步信号相位φ的相位差:

(23)

在DSP内进行一系列浮点计算可得:

(24)

式中:E为幅度控制;Q为正交控制;Ls为数字锁相环输入;S为驻波的正弦分量;M为驻波的余弦分量;tan-1(S/M)计算得到驻波角度θ。

4 全角模式下进动因子校正与验证

为了减小检测误差对进动因子的影响,需要在驻波方位角解算过程中进行补偿,引入校正矩阵Ac,使得A′近似为单位矩阵,即:

A′=Ac×Ad×Ae≈I

(25)

若要得到校正矩阵Ac,则需测试检测通道X、Y的增益之比,以及通道之间的耦合系数,可在静态条件下分别对电路增益及通道耦合Ae和读出电极间隙Ad进行标定[8-9],但静态标定过程中引入的分布电容等因数对Ae、Ad的测试准确性有较大的误差,所以本文根据检测误差对进动因子的影响分析,提出了一种更准确的测试标定方法。陀螺加工、装配过程中产生的增益误差和耦合误差,统一考虑为x、y轴的检测误差。以通道x轴为基准,a11=1,a22=g(g为增益失配系数),a12=0,a21=δ。 由于阻尼和频差的周向分布不均匀带来的系统漂移每小时约为几十度,远小于转台的测试激励角速率为100 (°)/s,此项误差可忽略。

工作于全角模式下的半球谐振陀螺,陀螺驻波角度θ=α×h,h为外界载体旋转角度。为了测试全角模式下半球陀螺驻波的进动因子,将陀螺放置在速率转台上,输入轴朝上,以100 (°)/s匀速旋转。陀螺驻波角度θ以0.1 s采样。根据式(12) 可得:

(26)

根据式(18)在转速100 (°)/s下实测的进动因子随驻波角度的变化进行曲线拟合,结果如图3所示,然后求解得到增益失配系数g,以及通道耦合系数δ,最后进行参数校正。

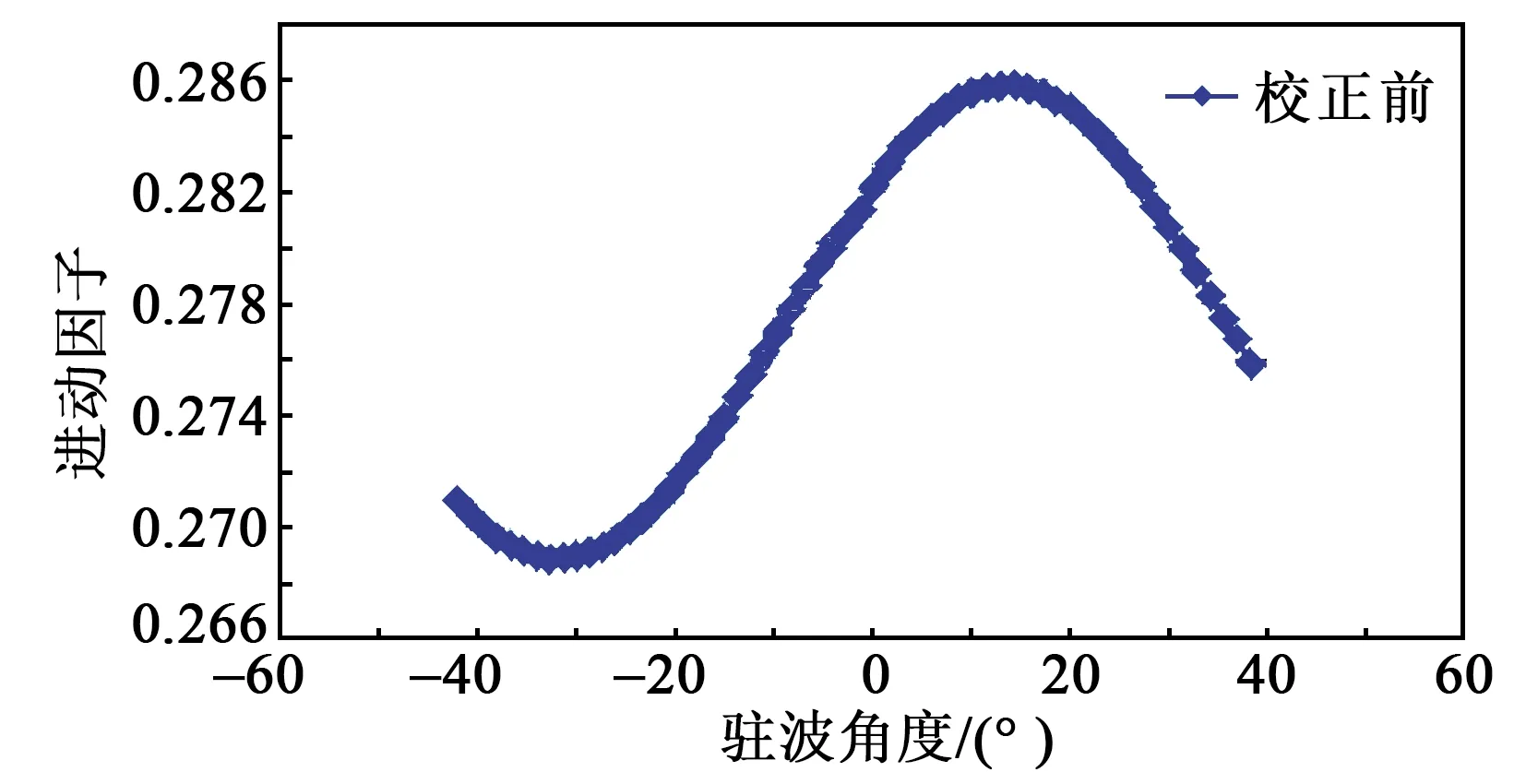
图3 校正前进动因子随驻波角度的周向分布

图4为检测误差校正前进动因子随时间变化。由图3、4可看出,检测误差校正前,进动因子随驻波角度和时间的周期性变化峰-峰值约为0.18,进动因子最大与最小比约为1.063。图5为检测误差校正后进动因子随驻波角度的周向分布。图6为检测误差校正后进动因子随时间变化。由图5、6可看出,检测误差校正后,随驻波角度及时间的周期性变化,进动因子峰-峰值降低到0.000 2,对比校正前的0.18,提升了约2个数量级,且进动因子与理论值(0.277)相符。进一步分析图5、6可知,检测误差校正后,进动因子还有约0.000 2的残余误差,且呈周期性变化,说明还有其他残余系统误差存在,如读出与驱动过程中的非线性等[10],还需进一步研究。

图4 校正前进动因子随时间变化

图5 校正后进动因子随驻波角度的周向分布

5 结束语

本文以基尔霍夫-李雅夫假设为基础,建立理想谐振子壳体动力学模型,求解薄壳表面任意质点运动方程,从机理上推导出理想谐振子进动因子只与其物理形状尺寸相关,具有较好的一致性。结合实际的谐振子与全角模式控制电路,由于读出电极间隙误差和检测电路的增益失配等检测误差,推导出进动因子不再为常数,而为驻波方位角θ的函数α′(θ)。然后给出了具体的校正方法。经实验验证,进动因子的周向一致性提升了约2个数量级。实际的半球陀螺检测电路还有一定的非线性,将对进动因子的稳定性及其测试精度造成影响。后续研究可在此基础上扩展,进一步提升进动因子的周向一致性。