重组竹顺纹力学性能的代表性体积单位模型1)

2023-05-31刘曼伍希志张永超李贤军

东北林业大学学报 2023年6期

刘曼伍希志张永超李贤军

(中南林业科技大学,长沙,410082)

重组竹是一种包含维管束、基本组织、树脂和界面的多相复合材料[1-2],具有各向异性、不均匀性和损伤模式多样性等特点[3-4],其损伤过程是一个包含纤维断裂,基体失效,纤维基体界面脱粘的复杂非线性渐变过程。在实际使用中,由于载荷形式复杂,损伤模式之间相互影响,表现出更复杂的耦合损伤行为[5-7]。在重组竹力学性能的研究中,Huang et al.[8]通过试验研究了毛竹纤维方向上的单轴应力-应变关系,其顺纹抗拉应力-应变关系呈完全线性关系,为脆性破坏;而其顺纹抗压应力-应变关系具有明显的非线性,为塑性破坏,非线性部分可以通过二次多项式。Li et al.[9]通过大量实验研究了重组竹的基本力学性能与应力-应变关系,提出了四线性模型、二次函数模型、三次函数模型来预测弹塑性阶段的应力-应变关系。

以上国内外研究现状表明,国内外学者大多采用试验手段和基于维象理论,研究重组竹的应力-应变曲线及力学性能理论模型,没有从微观力学的尺度建立重组竹代表体积单元,更准确地描述重组竹宏观力学性能同其组分材料及微观尺度结构之间的定量关系[10]。采用微观力学理论建立重组竹RVE模型,研究了不同纤维分布方式、纤维与基体组分材料参数以及纤维所占体积比,对重组竹代表性体积单元力学性能的影响。为后续竹片的自动化检测奠定了基础。

1 材料与方法

重组竹材料取自湖南桃花江竹材科技股份有限公司,参照GB/T 1938-2009《木材顺纹抗拉强度试验方法》、JG/T 199-2007《建筑用竹材物理力学性能试验方法》、GB/T 1935-2009《木材顺纹抗压强度试验方法》、GB/T 1577-2017《木材顺纹抗压弹性模量测定方法》,制作重组竹顺纹抗拉试件(图1),顺纹拉伸强度和弹性模量在同一批试件上完成,重组竹顺纹抗压强度与弹性模量试件均为长方体,其尺寸分别为:30 mm×20 mm×20 mm、60 mm×20 mm×20 mm,每种试件各5个。

R为半径

先进行顺纹拉伸弹性模量试验,再进行顺纹拉伸强度试验;顺纹压缩强度和顺纹压缩弹性模量分别在两批试件上完成。顺纹拉伸和压缩弹性模量试验程序设置为:以0.5 mm·min-1的速率加载至下限载荷,再以0.1 mm·min-1的速率加载至上限载荷,随即将载荷降至0.8倍下限载荷,再重新加载至上限载荷,反复加载6次。顺纹拉伸弹性模量试验结束后,以0.5 mm·min-1的速率将试件拉断,测试试件顺纹拉伸强度。顺纹抗压强度试验,以0.5 mm·min-1的速率将试件压溃。记录整个过程中的载荷、位移与应变,应变采用东华ST3827动静态测试系统记录(图2)。

图2 重组竹顺纹拉压力学性能试验图

重组竹试件顺纹力学性能计算方法[11]如下:

(1)

式中:σ1为顺纹极限应力(单位GPa);F1为顺纹极限抗拉(抗压)载荷(单位kN);b和t分别为试件有效部分宽度和厚度(单位mm);E1为顺纹抗拉或抗压弹性模量(单位GPa);ΔF1顺纹载荷增量(单位kN);Δε1为横纹方向应变增量;Δε2为顺纹方向应变增量;v12为泊松比。

单个纤维面积测定:采用电子显微镜放大100倍观察并拍照,图3(a)为电子显微镜下单个纤维的横截面形貌。将图片下方标注信息截除,确保每张图片的像素点个数为768×1 024,采用PS软件勾勒图片中单个纤维的轮廓,将纤维外的图片处理为黑色(图3(b))。采用MATLAB软件进行图像处理,从拍摄的16张电子显微镜图片中,计算出单个纤维的面积(表1)。单个纤维横截面平均面积为198 527 μm2、标准差为31 698 μm2、变异系数为15.97%。

图3 单个纤维电镜扫描图

表1 单个纤维面积

纤维面积比测量:将试件置于体式显微镜下放大10倍后拍照[12](图4)。本研究不考虑单个纤维面积的差异,不考虑纤维破坏对重组竹力学性能影响,假设试件纤维总面积等于单个纤维平均面积乘以纤维数量。各试件中间有效区域取样的纤维面积比(图5),图中编号“SL”表示顺纹拉伸试件,而后两个数字表示试件的编号,例如,SL01表示第1个拉伸试件,但由于每个拉伸试件破坏形式不同,图中每个拉伸试件的有效取样数量也不同。5个试件取样的纤维面积比在一定范围内波动(图5),5个试件的平均纤维面积比分别为:39.9%、40.8%、42.8%、41.9%、40.1%,变异系数分别为1.8%、2.2%、4.4%、3.2%、2.5%,5个试件的总平均纤维面积比为41.1%。

图4 体式显微镜下纤维横截面

重组竹代表性体积单位(Representative Volume Element,RVE)模型尺寸的确定:在建立重组竹的RVE模型时,将纤维等效为圆柱体,其底面积等于纤维的平均横截面积,为了研究RVE模型的最小尺寸,Trias et al.[13]认为纤维长度与底面半径之间的关系影响RVE的尺寸,在应力场均值的检验假设中纤维长度与底面半径之比应大于10,经计算重组竹RVE模型仿真中横截面的纤维根数数应大于13。为了使RVE模型能尽可能描述微观结构的所有信息,此次仿真选择包含25根纤维的RVE模型。RVE模型中纤维半径(R)和边长(L0)的计算如下:

(2)

(3)

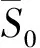
“SL”表示顺纹拉伸试件。

组分材料参数计算:组分材料参数包括纤维和基体的弹性模量,通过混合定律[14]进行计算。由于重组竹抗拉和抗压弹性模量基本相同,本研究认为纤维和基体的抗拉弹性模量与抗压弹性模量相同,以顺纹拉伸试件进行组分材料参数计算。

根据混合定律,拉伸或压缩时重组竹与其组分材料应变相同:

ε=εf=εm。

(4)

式中:ε为复合材料应变;εf为纤维的应变;εm为基体的应变。

当外加应力作用与重组竹横截面(A),纤维与基体平行的承受应力,则有:

F=Ff+Fm;

(5)

(6)

km+kf=1;

(7)

E=kfEf+kmEm=kf(Ef-Em)+Em。

(8)

式中:σ、σf、σm分别代表复合材料、纤维、基体的应力(单位MPa);kf、km,分别代表重组竹的纤维和基体的体积分数;E、Ef、Em分别代表重组竹、纤维、基体的弹性模量(单位MPa)。

根据公式(7),利用重组竹抗拉试件的抗拉弹性模量与纤维面积百分比试验数据,利用Matlab软件进行线性拟合[15],得到重组竹顺纹抗拉弹性模量与纤维百分比之间的线性关系式(9),线性拟合相关系数R2为0.999 8。对比公式(8)可得,纤维的抗拉弹性模量为30 335 MPa,基体的抗拉弹性模量为1 049 MPa。

E=29 286kf+1 049。

(9)

式中:E为重组竹抗拉弹性模量(单位MPa);kf为纤维所占体积分数。

纤维随机分布RVE模型采用随机顺序分配算法[16]生成一个纤维随机分布截面的2D模型,再将2D模型转化为3D模型。建立过程如下:(1)使用MATLAB软件编写纤维随机分布程序,程序包括3个输入参数:RVE边长(L)、纤维体积分数(Vf)和纤维直径(d),相邻纤维中心之间的距离大于1.035倍的纤维直径。(2)在Python软件中编写一个纤维随机分布的2D RVE模型脚本,当MATLAB中生成的纤维中心与RVE边缘间距小于0.5倍的纤维直径,纤维几何分成两半,根据周期性变化条件,纤维的另一半手动添加在下1个周期。(3)在ABAQUS中执行Python脚本,创建2D模型,再将2D模型的纤维横截面图重命名保存,仿照纤维均匀分布RVE模型生成方式,将2D模型的纤维横截面图复制到3D模型中,生成纤维随机分布的3D模型如图6(b)。

图6 重组竹代表体积单元的3D模型

RVE模型加载与求解:为了让相邻RVE模型之间的连续性得以保持,周期性边界条件应用于RVE模型的边缘,在这一条件下导出的力学行为始终受到施加力或位移的约束。设X1、X2、X3为笛卡尔坐标轴,X1和X2分别平行于RVE横截面两边,原点位于RVE的横截面角。在周期性RVE的边界上其位移可表示为:

(10)

(11)

(12)

两式相减可得:

(13)

图7 重组竹RVE模型边界条件

2 结果与讨论

2.1 失效模式

图8为试件失效模式,抗拉试件的失效模式与抗压试件不同。抗拉试件失效模式(图8(a)),基体与纤维几乎在同一时间从中间位置拉断,断裂形状呈一字锯齿型。抗压试件失效模式(图8(b)),在荷载加载过程中,试件在顺纹方向发生压缩,在横纹方向发生伸长;在变形过程中,竹纤维之间的胶层界面应力不断增大;当界面应力大于界面粘结结度时,胶层界面发生剥离,逐渐形成微裂纹,并沿顺纹方向扩展成大裂纹;随着荷载继续增加,试件发生局部屈曲,停止试验加载,可以明显观察到裂纹。抗压试件破坏形状通常为两端小中间大,这是因为试件端部与钢板接触,钢板的弹性模量远远大于重组竹的弹性模量,同样压力载荷下钢板的变形远远小于重组竹的变形,从而使重组竹试件端部与钢板之间产生摩擦力,限制重组竹试件横向膨胀。

2.2 顺纹力学性能

图9为试件的载荷-位移曲线,重组竹顺纹抗拉试件的载荷-位移曲线基本呈线性关系,在加载前期由于试件与夹具之间存在空隙等原因,载荷-位移曲线有一定的抖动现象,随着加载力的增大,载荷-位移曲线线性关系逐渐稳定,在试件破坏时,其载荷发生突变。顺纹抗压载荷-位移曲线是非线性的,可分为四个阶段:第一阶段为线弹性阶段(0～25 kN),载荷-位移曲线呈线性增加,直至比例极限,但在载荷达到7 kN时,曲线的斜率会有小幅度下降,这是由于试件受压时上表面与加载面不平行,导致试件受力不均匀;第二阶段为塑性变形阶段(25 kN至极限载荷),当载荷超过弹性极限后,载荷-位移曲线呈非线性增加;第三阶段为屈曲阶段,达到极限载荷后,试件的位移不断增加,载荷基本保持不变;第四阶段为失稳阶段,随着位移不断增加,载荷不断减小。

图8 试件失效模式

重组竹顺纹力学性能如表2,重组竹顺纹抗拉弹性模量平均值为12.706 GPa,变异系数为2.570%,顺纹抗压弹性模量平均值为12.826 GPa,变异系数为11.540%,顺纹抗拉弹性模量与顺纹抗压弹性模量基本相等,顺纹抗拉弹性模量比顺纹抗压弹性模量波动小。重组竹顺纹抗拉极限强度平均值为104.580 MPa,变异系数为13.380%,顺纹抗压极限强度平均值为82.670 MPa,变异系数为6.020%,顺纹抗拉极限强度比顺纹抗压极限强度大21.910 MPa,顺纹抗拉极限强度比顺纹抗压极限强度波动大。由于顺纹抗压强度试件发生了粘接界面剥离和局部屈曲,所以顺纹抗压强度比顺纹抗拉强度小。重组竹顺纹抗拉泊松比平均值为0.320,顺纹抗压泊松比平均值为0.350,其中顺纹抗拉泊松比的变异系数为6.560%,顺纹抗压泊松比变异系数为15.320%。由于顺纹应变基于两个应变片的平均值所得,而横纹应变是基于一个应变片所得,所以顺纹抗拉与抗压泊松比的差异较大。

2.3 有限元模型验证

根据重组竹顺纹抗拉试验结果可得,其平均抗拉极限应变为0.008 2,将抗拉仿真模型的位移设置为28.44 μm,使仿真模型的应变与抗拉极限应变相等,当拉伸位移为28.44 μm时,根据ABAQUS单位换算,此时纤维的应力值为249.7 MPa,基体的应力值为8.049 MPa,纤维的应力远大于基体的应力(图10)。根据纤维所占横截面的面积比为41.1%,可计算出纤维承受载荷占重组竹RVE模型载荷的96.30%,纤维承受了主要载荷。

(a)为顺纹抗拉载荷-位移曲线;(b)为顺纹抗压载荷-位移曲线。

表2 试件的顺纹力学性能试验结果

图10 重组竹顺纹拉伸应力云图

重组竹RVE模型仿真与试验结果对比(图11),(1)顺纹抗拉仿真结果与试验结果比较吻合,顺纹抗压仿真结果与试验结果有些差异,具体表现为:在弹性变形阶段,顺纹抗压仿真结果与试验结果比较吻合,超过弹性极限后,仿真应力-应变曲线仍然是线性变形,试样应力-应变曲线是非线性的,这是由于仿真模型的基体和纤维材料属性均是弹性的,且没有考虑粘接界面剥离的影响;(2)纤维均匀排列与随机排列的拉伸、压缩的应力-应变曲线非常相近,说明纤维排列方式对重组竹顺纹弹性模量的影响较小。纤维均匀排列与随机排列的重组竹RVE模型弹性模量分别为12 019、12 166 MPa,对比试验结果的抗拉弹性模量12 706 MPa,仿真结果与试验的误差分别为5.4%和4.2%,说明仿真结果与试验结果比较吻合。

2.4 参数分析

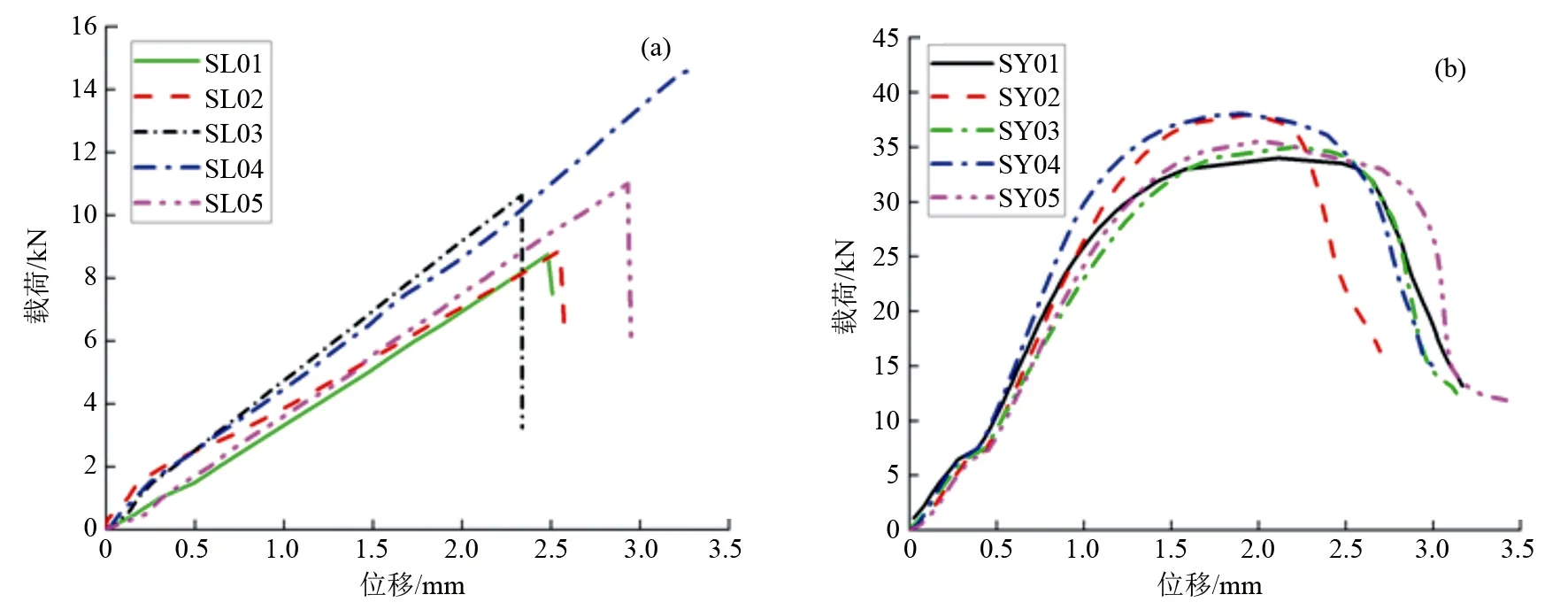
图12(a)表示当基体的弹性模量保持为1 GPa不变时,纤维弹性模量分别为30、35、40 GPa时RVE模型的载荷位移曲线,而图12(b)表示当纤维弹性模量保持30 GPa不变时,基体弹性模量分别为1、6、11 GPa时RVE模型的载荷位移曲线。由图12可知,纤维弹性模量35 GPa的RVE模型弹性模量比纤维弹性模量30 GPa增加17%,纤维弹性模量40 GPa的RVE模型弹性模量比纤维弹性模量35 GPa增加14%。而基体弹性模量分别为1、6、11 GPa的RVE模型弹性模量变化不明显,载荷位移曲线几乎重合。

图13表示不同纤维体积分数的RVE模型顺纹拉伸载荷位移曲线,纤维体积分数分别为30.0%、41.1%、50.0%,采用纤维均匀分布RVE模型,从图中可以看出,纤维体积分数为30%的RVE模型比41.1%的RVE模型顺纹弹性模量减少15%,纤维体积分数为50.0%的RVE模型比41.1%的RVE模型顺纹弹性模量增加30%,纤维体积分数对RVE模型顺纹弹性模量影响较大。