分析型光压模型在北斗导航卫星精密定轨中的应用

张国亭 王宏 黄勇 郑世贵 王振兴

(1 国防科技大学 空天科学学院,长沙 410073)(2 北京跟踪与通信技术研究所, 北京 100094) (3 中国科学院上海天文台,上海 200030)(4 北京空间飞行器总体设计部, 北京 100094)

我国的航天事业发展迅猛,对卫星的定轨精度要求也越来越高。在卫星动力学定轨过程中,有两种难以精确模制的非引力摄动:大气阻力摄动和太阳光压摄动。对于中高轨道卫星,由于没有大气阻力摄动且对地球非球形引力摄动也不敏感,因此太阳光压摄动成为继地球引力,日月引力之后量级最大的摄动,特别是导航卫星动力学定轨建模误差最大的摄动力,也是研究的热点方向[1]。以我国北斗导航卫星为例,相比于中地球轨道(MEO)卫星,地球静止轨道(GEO)和倾斜地球同步轨道(IGSO)卫星轨道高度较高,受到的太阳辐射压影响更大[2]。

太阳辐射压对卫星产生的摄动加速度与太阳辐射强度、卫星相对于太阳的姿态和位置、卫星的面质比、几何形状及其表面材质的物理特性等因素有关。由于太阳辐射强度的变化、卫星姿态控制的偏差以及卫星表面材料的老化等因素,太阳辐射压摄动较难进行模制,它已经成为高轨卫星动力学定轨最主要的误差源。

太阳辐射压模型根据建模原理方法的不同可以分为物理分析模型和经验模型。物理分析模型是指基于卫星的结构和表面的光学特性所建立的模型。经验模型是指拟合卫星的在轨数据得到的模型。此外,还有一类模型,建模时既使用了卫星的基本信息,又使用了卫星的在轨数据,称半经验模型。这几种模型都曾或仍然被广泛使用,各有优缺点,对于卫星太阳辐射压建模具有重要的借鉴意义[3-6]。

目前,导航卫星精密定轨广泛采用扩展经验光压模型(ECOM)等经验模型[7-8],不仅用于全球定位系统(GPS)的定轨计算,GPS/GLONASS的联合定轨和北斗导航卫星定轨也常会采用该模型来模制太阳辐射压摄动[9],并得到较好的结果。ECOM模型使用9个参数分别对三轴上太阳辐射压摄动的常数项和周期项进行拟合吸收,不仅吸收太阳辐射压建模的缺陷,而且还能吸收一些其他未模制的力的影响,提高定轨的精度。另外,ECOM模型不使用任何先验模型,直接估计三轴上的太阳辐射压摄动,也能取得较好的定轨结果。然而,想要取得较高的定轨精度,必须要有足够的在轨观测数据,因此ECOM等经验模型不适用在轨运行初期的卫星的定轨工作。ECOM参数模型完全是一个经验模型,需要大量的在轨数据来拟合,待估参数的增多会影响法方程性能。另外,多少时间拟合一组参数,也是一个值得研究的问题。

经验模型虽然可以取得较高的定轨精度,但是其估计的参数没有实际的物理意义,无法揭示太阳辐射压摄动对卫星轨道影响的物理机制。尤其对于在轨运行初期的卫星,没有足够的在轨观测数据,很难通过经验模型获取较好的定轨结果。因此,建立高精度的分析型太阳辐射压模型是非常有必要的。

本文以我国北斗导航卫星作为研究对象,研究了分析型光压模型在北斗GEO和IGSO等高轨卫星定轨中的应用,首先介绍了分析型光压的建模原理,然后选取了一颗北斗GEO卫星和一颗IGSO卫星进行了分析,比较了分析型光压结果和精密定轨结果的差异,并利用分析型光压模型进行精密定轨,精度约为分米级。

1 分析型光压建模原理

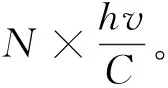
考虑一个“无限小”面元ds:

(1)只考虑光子的吸收和镜反射,作用于面元上的光压力为(如图1所示)

dF=dF1+dF2

(1)

式中:dF1和dF2分别为面元ds受到的吸收作用力和镜反射作用力,有

(2)

dF2=-ρs|dF1|dr

(3)

式中:n为面元ds的法向单位矢量;d为入射方向的单位矢量;dr为反射方向的单位矢量;ρs为面元ds的镜反射系数。

F2的方向符合镜反射规律,但其大小与面元的镜反射系数有关。于是光压力又可表达为

(4)

式中:θ为入射方向单位矢量d与面元ds的法向单位矢量n的夹角;dscosθ为面元ds在垂直入射方向的投影。

将dr用已知方向d和n来表达,有

(5)

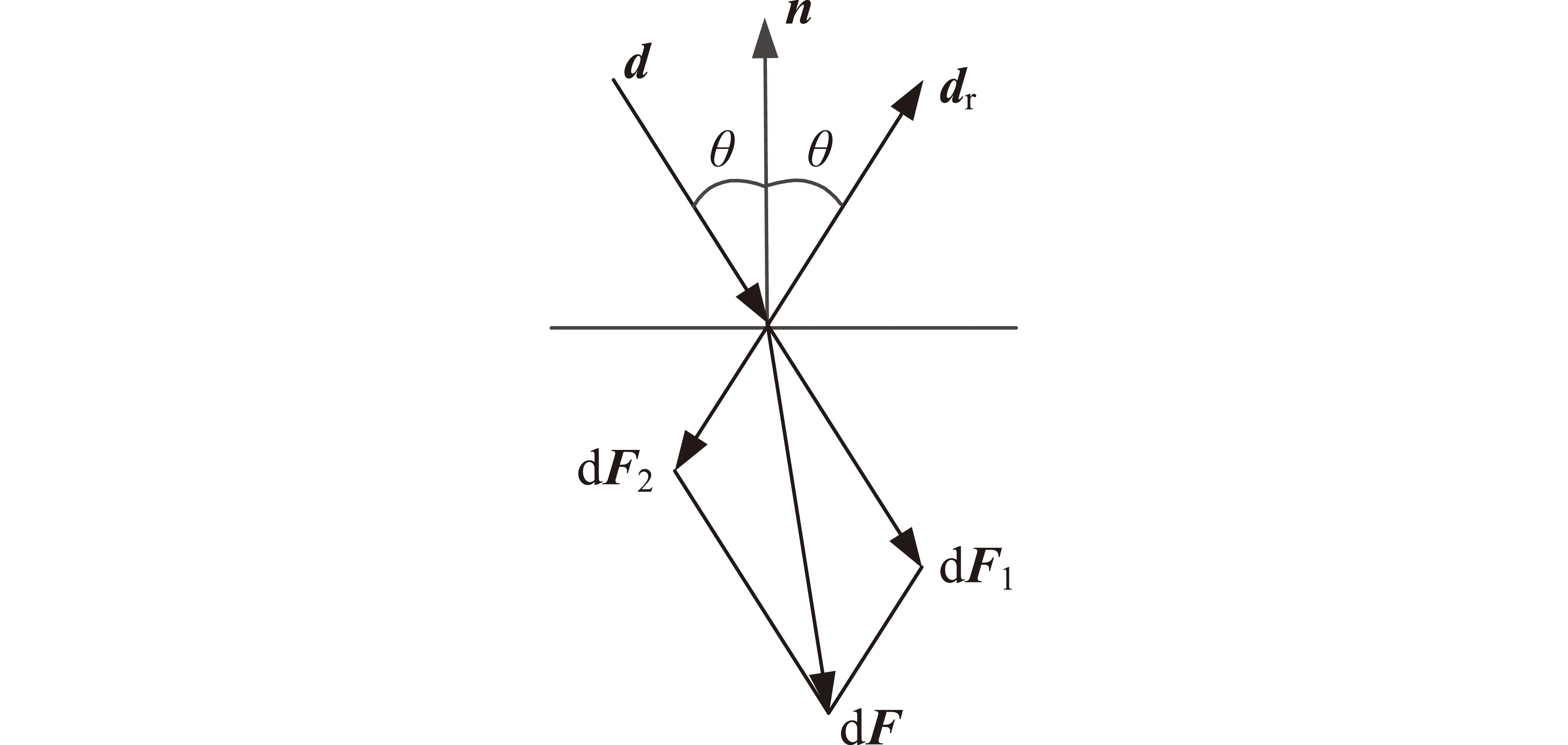
图1 面元上的光压力示意Fig.1 SRP on the face

(2)只考虑光子漫反射,漫反射遵从cos法则,该法则假设反射方向分布正比于反射方向与面法向夹角的cos值。漫反射关于面法向对称,平均反射速度方向即为面法向方向,作用于面元上的光压力为

(6)

式中:ρe为漫反射系数。

综合光子的吸收、镜反射和漫反射,作用于面元ds上的光压力为

(7)

该模型包含了光子在材料表面的各种行为,但要准确获得表面的光学性质比较困难,而且在空间环境的长期作用下,材料表面的光学性质会发生变化。

本文采用的是基于蒙特卡洛射线追踪算法计算光压,蒙特卡洛法又称随机模拟法或统计试验法,是一种依据统计抽样理论,利用计算机研究随机变量的数值计算方法。基本原理为在状态变量的概率分布已知且相互独立的条件下,随机产生符合状态变量概率分布的随机数,然后以这些随机数为基础生成服从某一分布的状态函数,进行后续分析。

射线追踪算法是追踪射线路径上与射线相交的所有面,计算出射线与面元的所有交点,然后只考虑距离射线出发点最近的交点。

射线追踪一般步骤如下:

(1)确定一个平行六面体封闭盒,该盒包含全部几何模型;

(2)把封闭盒分成许多等尺寸的方块;

(3)对于每一个方块,列出落在方块中的所有面,这些面至少有一个点落在方块中;

(4)依照射线前进方向,依次计算射线路径上的方块;

(5)检查射线与当前方块中的所有面是否有交点,如果存在交点且交点位于当前方块中,执行(6),否则返回(4)计算下一个方块;

(6)找出距离射线出发点最近的交点完成一次光压计算。

离散空间中的射线追踪顺序示意见图2。

可把太阳入射光看成一定数量光线的集合,每条光线相互独立。由于航天器距离太阳非常远,可认为所有光线为平行光线。如果光线数量足够就能够模拟太阳入射光产生的压力效应。计算光线的一次撞击,同时考虑光子与表面的镜反射、漫反射与吸收效应。采用射线追踪算法的计算误差约为射线数开平方分之一。如10000条射线,则光压力的误差为1%。基于射线追踪算法的光压分析程序流程如图3所示。

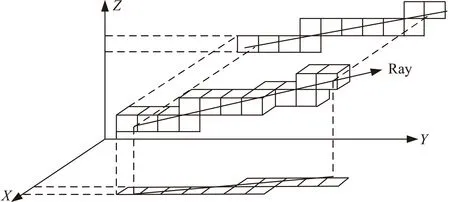
图2 射线追踪顺序示意Fig.2 Ray tracing sequence

图3 基于射线追踪算法的光压分析程序流程Fig.3 Steps of the analytical SRP model program based on ray tracing approach

影响光压分析精度的因素有卫星几何模型、表面材料光学参数、太阳辐射强度、光压模型、数值计算方法(本文方法为射线数)等。

2 北斗卫星分析型光压模型精度评估

随着伽利略(Galileo)卫星导航系统和北斗卫星导航系统的逐步建设和完善,以及GPS系统和GLONASS系统逐步现代化推出更多新的民用信号,国际GNSS服务组织(IGS)于2012年着手在全球范围内构建多模GNSS系统试验网络(Multi-GNSS EXperiment,MGEX),实现对GPS、GLONASS、Galileo、北斗和其他卫星导航系统的跟踪和监视,为新兴卫星导航系统的高精度数据处理提供了数据条件。基于MGEX全球监测站的北斗IGSO和MEO卫星定轨结果径向(R)误差优于10cm,三维轨道误差约为几十厘米,可以用于精密单点定位服务。但是全球跟踪网的增加,GEO卫星的轨道精度不会得到明显提升,约在米级。MGEX的定轨结果基于ECOM等经验光压模型[10]。

北斗GEO-6于2012年发射,星下点经度为80.3°E,北斗IGSO-5于2011年发射,星下点经度(赤道)为96°E。从MGEX网站下载了2016年3月3日至4月2日约1个月GEO-6和IGSO-5的精密星历(武汉大学分析中心结果),sp3c格式的卫星轨道为卫星地固系(WGS-84)下的X、Y、Z轴坐标值。将精密星历的X-Y-Z作为观测量对轨道进行逐天定轨,定轨参数包括初始轨道根数和经验型的ECOM5光压模型参数,统计定轨精度,并输出太阳辐射压摄动加速度。

图4为GEO-6和IGSO-5的定轨精度,GEO-6的定轨精度大部分时间优于0.2m,IGSO-5的定轨精度优于0.1m(时间起点为2016年3月3日)。

按照第1节分析型光压建模的原理,结合北斗卫星的几何尺寸和表面材料特征,以及探测器和太阳的相对位置等信息,可以计算得到北斗卫星的太阳光压摄动力。图5给出了利用分析型光压模型得到的GEO-6和IGSO-5卫星所受到的太阳辐射压摄动加速度,坐标系为RTN(轨道的径向R、横向T和法向N)。前述精密定轨输出的太阳辐射压摄动加速度时间序列与之类似,在RTN三个方向分别约为10-7、10-7和10-8m/s2量级,N方向受力比其他两个方向小一个数量级。频谱分析结果表明:GEO-6和IGSO-5卫星太阳辐射压摄动的主要周期为24h,和轨道周期一致。

将该值和前述精密定轨输出的太阳辐射压加速度进行比较,差异结果如图6和图7所示。

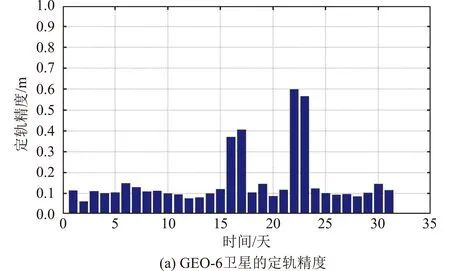
图4 基于经验光压模型的GEO-6和IGSO-5卫星的定轨精度Fig.4 Orbital accuracy of GEO-6 and IGSO-5 satellites based on ECOM

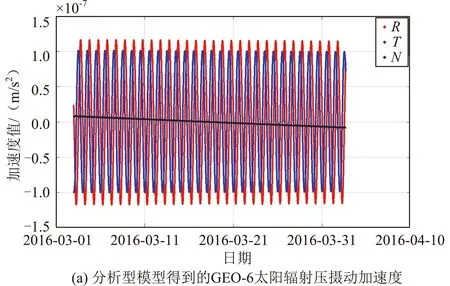
图5 分析型模型得到的太阳辐射压摄动加速度Fig.5 Analytical model of SRP perturbation acceleration

图6 GEO-6卫星的分析型光压结果和精密定轨结果差异Fig.6 Differences between analytical SRP results and precision orbit determination results of GEO-6 satellite

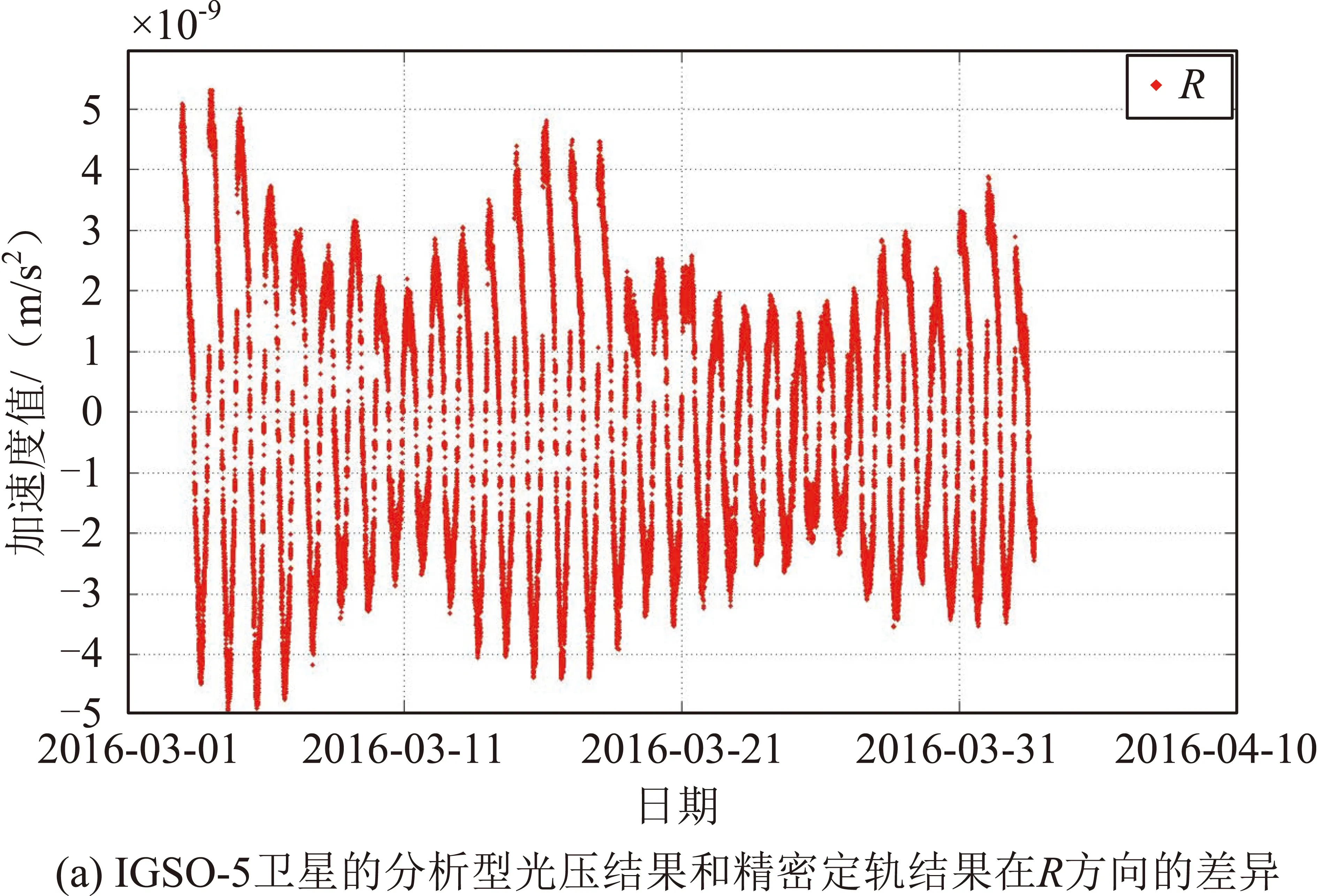
图7 IGSO-5卫星的分析型光压结果和精密定轨结果差异Fig.7 Differences between analytical SRP results and precision orbit determination results of IGSO-5 satellite

从上述分析结果可以看出:精密定轨输出的太阳辐射压加速度和分析型光压模型的结果比较,对GEO-6卫星,R和T方向差异在10-8m/s2量级,N方向在10-9m/s2量级,相对误差在10%左右。对IGSO-5卫星,差异要小1/2左右,约为5%。考虑到分析型光压模型的建模过程和精密定轨无关,而精密定轨输出的太阳辐射压加速度和精密定轨密切相关,IGSO卫星相比GEO卫星,分析型光压模型和精密定轨所采用的经验模型符合程度更好,这可能是由于IGSO卫星的定轨精度更高引起的。

3 分析型光压模型在导航卫星精密定轨中的应用

进一步分析分析型光压模型在北斗高轨卫星精密定轨的应用,一方面可以直接应用分析模型输出的太阳辐射压加速度时间序列来代替定轨软件中的光压模型;另一方面考虑到分析模型可能还存在一定的误差;可以对其增加若干调节参数,类似于对星载加速度计数据的处理方式,如下

aci=ai+ki×ami

(8)

式中:i=1,2,3(对应于RTN轴),aci为经过标校后的i方向的加速度值;ai为加速度常数偏差参数;ki为i方向的尺度因子参数;ami为观测值。标校参数在定轨时予以解算。

对GEO-6和IGSO-5卫星,如果直接使用分析型光压模型,以MGEX轨道作为参考轨道,定轨精度如图8所示(时间起点为2016年3月3日),GEO-6位置误差约在2.5m左右,IGSO-5位置误差约1.5m左右。

图8 直接使用分析型光压模型定轨精度Fig.8 Orbit accuracy is determined directly using analytical SRP model

增加标校参数(偏差和尺度因子),GEO-6和IGSO-5定轨精度如图9所示(时间起点为2016年3月3日),GEO-6位置误差小于1m,平均误差约为0.5m。解算出来的尺度因子接近于1,偏差参数约在10-9～10-8m/s2量级。相应IGSO-5的定轨精度比GEO-6的定轨精度均要高,增加标校参数后位置误差小于0.1m。

上述分析表明:分析型光压模型可能存在一定的系统性偏差,可以通过建模的方式对系统误差参数予以解算以提高定轨精度。从定轨结果看,基于分析型光压模型的IGSO卫星的定轨精度和常规经验模型定轨精度相当,而GEO卫星的定轨精度略低于常规经验模型,初步验证了分析性光压模型在北斗卫星精密定轨中的应用。

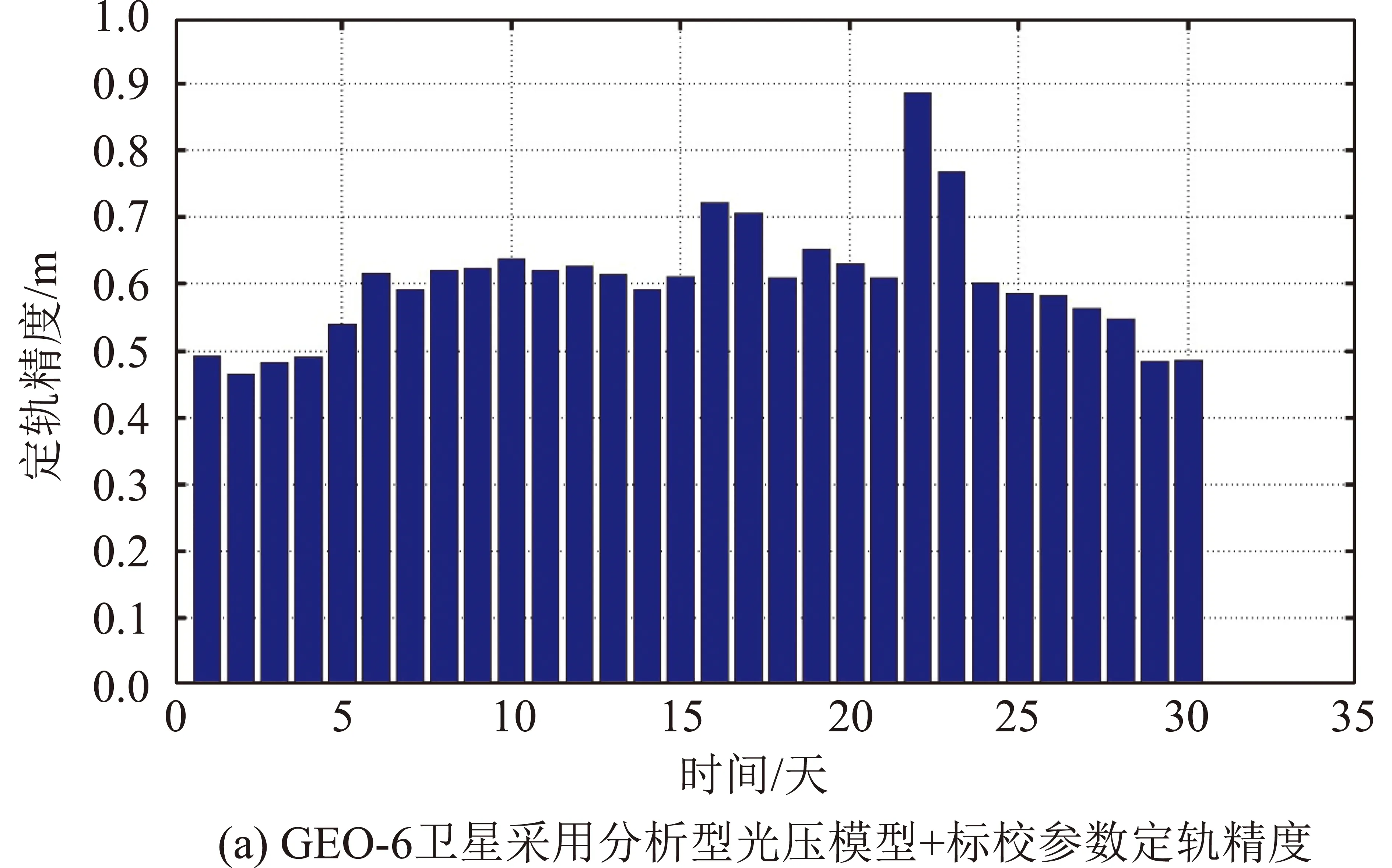
图9 分析型光压模型+标校参数定轨精度Fig.9 Analytical SRP model and calibration parameters orbit accuracy

4 结束语

本文分析了分析型光压模型在北斗高轨卫星精密定轨中的应用,对GEO-6和IGSO-5卫星建立了分析型光压模型,选取了2016年3月3日至4月2日约1个月的数据,将分析型光压模型结果和精密定轨输出的太阳辐射压加速度进行了比较,对GEO-6卫星,R和T方向差异在10-8m/s2量级,N方向在10-9m/s2量级,相对误差在10%左右。对IGSO-5卫星,差异要小1/2左右,约为5%。进一步分析分析型光压模型在北斗高轨卫星精密定轨的应用,直接使用分析型光压模型,以MGEX轨道作为参考轨道,GEO-6位置误差约在2.5m左右,IGSO-5位置误差约1.5m左右;增加偏差和尺度因子标校参数后,位置精度分别提高到0.5m和0.1m左右。本文分析结果表明:分析型光压模型可以应用于导航卫星精密定轨,以北斗GEO和IGSO卫星为例,可以实现分米级的定轨精度。该结果也可以应用于其他有精密定轨需求的高轨卫星,如果卫星刚进入轨道或者卫星进行轨道控制后,难以积累大量实测数据建立高精度的经验光压模型,在卫星发射前建立分析型光压模型,也是提高定轨精度的一种解决手段。