改进鸽群算法的复杂信号盲源分离 *

梁康博，杨瑞娟，李晓柏，骆伟林，袁凯

（中国人民解放军空军预警学院 预警情报系，湖北 武汉 430019）

0 引言

随着信息化智能化战争形态的不断发展，以及由军事强国推动的电磁频谱作战域对抗日趋激烈，主战装备的复杂电磁环境适应能力和智能化水平遇到了严峻挑战。采用侦干探通一体化技术，集雷达、干扰、侦察、通信功能为一体，一体化接收处理各种战场复杂电磁信号，为应对这种挑战提供了一个新的解决思路。侦干探通一体化接收处理前端可采用宽开接收机，将较大频率范围内的所有信号全部接收，并通过后端处理使得这些信号成为可用信号，这样既提高了处理的效能，又简化了硬件部分，而侦干探通一体化接收处理所面临的首要问题则是复杂混叠信号盲源分离（blind source separation，BSS）。

盲源分离，即根据观测信号恢复未知源信号［1］。盲源分离研究始于20 世纪末，由于在声音识别、信号分析等领域具有较好的应用前景，近些年来，盲源分离相关理论和应用都得到了较快发展［2］。独立成分分析［3］（independent component analysis，ICA）作为传统盲源分离经典算法，存在着易求得局部最优解的问题，分离效果较差。

为了解决传统算法存在的问题，选用群体智能算法与ICA 相结合，如狼群算法（wolf colony algorithm，WCA）［4］、蚁群算法（ant colony algorithm，ACA）［5］等。文 献［6-7］将 改 进 粒 子 群 算 法 结 合ICA，较好地分离出信号，但该算法速度较慢。文献［8］将改进狮群算法结合ICA，分离速度较快，效果较好，但需要调整的参数较多。

在群体智能算法中，标准鸽群算法（pigeoninspired optimization，PIO）［9］具有准确度较高、所需调整参数较少、收敛速度较快的特点，同时也有着易陷入局部最优、前期全局寻优和后期局部寻优算法资源分配不合理的缺点。本文针对上述问题提出一种改进鸽群算法的盲源分离方法（improved PIO，IPIO），通过不同环境下的仿真实验对算法性能进行测试，并分别与传统算法中比较具有代表性的 变 步 长 自 适 应 算 法［10］（equivariant adaptive separation via independence，EASI）以及改进前标准鸽群算法作比较，实验和性能分析结果证明，本文提出的方法具有更快的分离速度和更高的精度。

1 盲源分离原理

BSS 典型原理图如图1 所示。

图 1 盲源分离原理图Fig. 1 Principle of BSS

n个相互独立的源信号S(t) = (s1(t)，s2(t)，…，sn(t))T，经 过 信 道A混 叠 为X(t) = (x1(t)，x2(t)，…，xm(t))T，

通过优化算法计算分离矩阵B，得到分离信号

选用信号的负熵［11］为依据求得最佳分离矩阵B，负熵可表示为

式中：yg为与y均值方差都相同的高斯变量，改进鸽群算法中的适应度函数可以设为

式中：ε为防止除0 的一个极小量。J(y)越大，说明分离效果越好。

2 改进鸽群算法

2.1 基本鸽群算法

鸽子有着非常出众的方向感，而影响鸽群归巢的主要因素有3 种，即磁场、太阳和地貌景观。Guilford 等认为鸽子在飞行过程中的不同阶段会选择不同参照进行导航，在距离目标较远的开始阶段，鸽子利用磁场来判断方向，而在距离目标较近时就利用地标进行导航［12-13］。Whiten 则认为太阳也是影响鸽子的导航的一种因素，即太阳当时的高度会对鸽子方向感造成影响。PIO 就是模拟鸽子归巢行为设计出来的群体智能优化算法，该算法具有原理简单、参数较少、鲁棒性较强，容易实现的特点。

鸽群算法主要包括两部分，即地图和指南针算子、地标算子。

2.1.1 地图和指南针算子

该算子中，鸽群每个个体代表一个最优解。个体属性由位置和速度确定，假设某个鸽子群体中有i只鸽子，它们的位置和速度分别记为X=(X1，X2，…，Xi)，v= (v1，v2，…，vi)，那么，每个个体的位置、速度如下：

式中：t为迭代次数；R为算子因数，且R∈(0，1)；r为满足[0，1)的随机数；Xg为当前最好位置。

该部分可以看出，第i只鸽子的速度是由它上一次迭代时的速度和当前鸽子的最好位置共同决定的，而第i只鸽子的位置是由它上一次迭代时的位置和当前速度共同决定的。所有鸽子的飞行通过地图保证，比较可得鸽子的最好位置，即Xg。

该模型中，寻优的决策主要有2 个方面，一方面鸽群中所有个体都向全局最优位置靠近，另一方面在速度继承上成指数关系。前者提高了算法收敛速度，后者则提升了全局搜索的能力。令g(t) = e-Rt，当R= 0.5 时，函数g(t)如图2 所示，当t≈12 时，停止全局搜索，假设最大迭代次数T= 100，那么从13次迭代后，算法的（5）式将变为vi(t) =r(Xg-Xi(t- 1))，即鸽群过早在Xg聚集，如果该位置为局部最优位置，解就为局部最优解。

图 2 函数g（t）曲线图Fig. 2 Curve of function g（t）

2.1.2 地标算子

地标模型根据鸽子利用地标进行导航而建立。该算子中，每次循环，鸽群中减少适应度差的一半，计算剩余个体中心位置Xc，并依据下列公式对每只鸽子的位置进行更新：

式中：Np为鸽群数量；fitness()代表每个解的质量，此时鸽群的参考方向为一些较优个体的位置中心。

设Npmax= 100，迭代次数为100 次，如表1 所示，迭代8 次之后，个体数量为1，式（9）变为Xi(t) =Xi(t- 1)，此时后续都由单个个体进行搜索，算法早熟收敛，易陷入局部最优。

表 1 种群数量变化Table 1 Change in population

2.2 改进鸽群算法

2.2.1 地图和指南针算子中的位置因子

根据2.1.1 节中的描述，可以发现基本鸽群算法具有易早熟收敛、陷入局部最优的缺陷。为了解决该问题，本文在基本鸽群算法的基础上，提出一种位置因子。首先，随着算法运行次数增加，让运动权值非线性减小，该变化类似于余弦函数在前半个周期的变化趋势［14］。然后，让最优位置权值递增。这样，随着迭代次数增加，运动权值减小同时最优位置权值增大，将算法前期全局探索和后期局部更新能力进行平衡［15］，更好地引导鸽群进行寻优搜索。可将式（5）更新为

式中：

g为运动权值，表示对上一次迭代时速度继承的比例，且g∈[0，1]；h为最优位置权值，表示最优位置对当前速度更新的影响比例；i，j，m，n为常数，Tmc为该算子中的最大迭代次数。

可以看出，当t∈[0，T]时，g始终在减小，说明全局搜索能力在逐渐变弱，而h的值则一直在增大，说明最优位置附近的局部精确搜索能力在逐渐变强，这样既避免了早熟收敛，又能使得寻优结果准确率较高。

2.2.2 地标算子中的压缩因子

在2.1.2 中描述了地标算子的特点，鸽群数量按照每次迭代减少1/2 的速率下降，过快的衰减速度导致后期个体数量不足，在最优位置附近的局部精确搜索能力较差，寻优性能受到影响［16］。

本文提出一种分段控制鸽群数量的方法，即

式中：Npmax为初始鸽群数量。这样，既能保证前期鸽群数量较多，全局搜素能力较强，又能避免后期个体数量不足影响寻优性能，进入早熟收敛的问题。

同时，文献［17］中提出了一种收缩因子，用于压缩地标算子，提高全局搜索能力。式（9）可以替换为

式中：s为(0，1)之间的常数；Tl为最大迭代次数。

2.2.3 改进鸽群算法

将2.2.1 节中提出的位置因子和2.2.2 中提出的压缩因子相结合，得到算法的函数为

在地图和指南针算子中

式中：Tm为接近Tc的值；Tc为该算子的最大迭代次数。

在地标算子中

式中：Tt为大于1 小于Tl的值，且Tt的值更接近于1；Tl为该算子的最大迭代次数。

2 种算子中分别添加了改进因子，这样在寻优求解的过程中，两者互相作用，避免陷入局部最优，使得算法前期全局探索和后期局部更新能力进行平衡，增强了算法准确性。

3 基于IPIO 的盲源分离方法

3.1 Givens 矩阵

Givens 矩阵为如式（18）形式的矩阵：

G(p，q，θp，q)是n阶方阵，其中1 ≤p≤n，p＜q≤n。

定 理1［18］：任 意 的n阶 正 交 矩 阵Qn×n，存 在L=n(n- 1)/2 个Givens 矩阵G(p，q，θp，q)，使得

那么可以得出，若n=3，分离矩阵B可表示为

这样，在求得分离矩阵B的过程中，原本需要求解n2个相关参数，计算量较大，通过该定理简化，减少为n(n- 1)/2，降低了算法计算量。而求得分离矩阵后，则可以根据公式（2）计算恢复出源信号。

3.2 算法步骤和流程

3.2.1 算法步骤

step 1： 收集观测信号，并进行信号数据的预处理。

step 2： 初始化算法相关参数，包括各个算子迭代次数、种群个数、问题维数、位置因子、压缩因子、问题上下界等。

step 3： 基于问题维数为每个个体随机生成初始位置和初始速度。

step 4： 计算个体的适应度值，挑选全局最优解。

step 5： 进入地图与指南针迭代过程，在循环次数内，根据式（10），（14）进行速度与位置的更新。

step 6： 将step 5 中输出种群作为地标迭代的输入值，在循环次数内，依据适应度值对鸽群进行从优到劣的排序，根据式（13）舍去后面一部分个体，将留下的部分重新计算种群最优位置，并根据式（16），（17）更新个体位置。

step 7： 迭代结束，输出算法最优解，得到分离矩阵B，并计算恢复出源信号。

3.2.2 算法流程图

算法流程图如图3 所示。

4 仿真分析

假设源信号为侦干探通4 路信号，考虑正定盲源分离模型，设置4 路接收通道，其中侦查信号和探测信号选用雷达信号中的线性调频信号，干扰方式选择灵巧干扰［19］，通信信号选择8QAM 信号。4 路信号采用线性混叠的方式。如表2 所示。

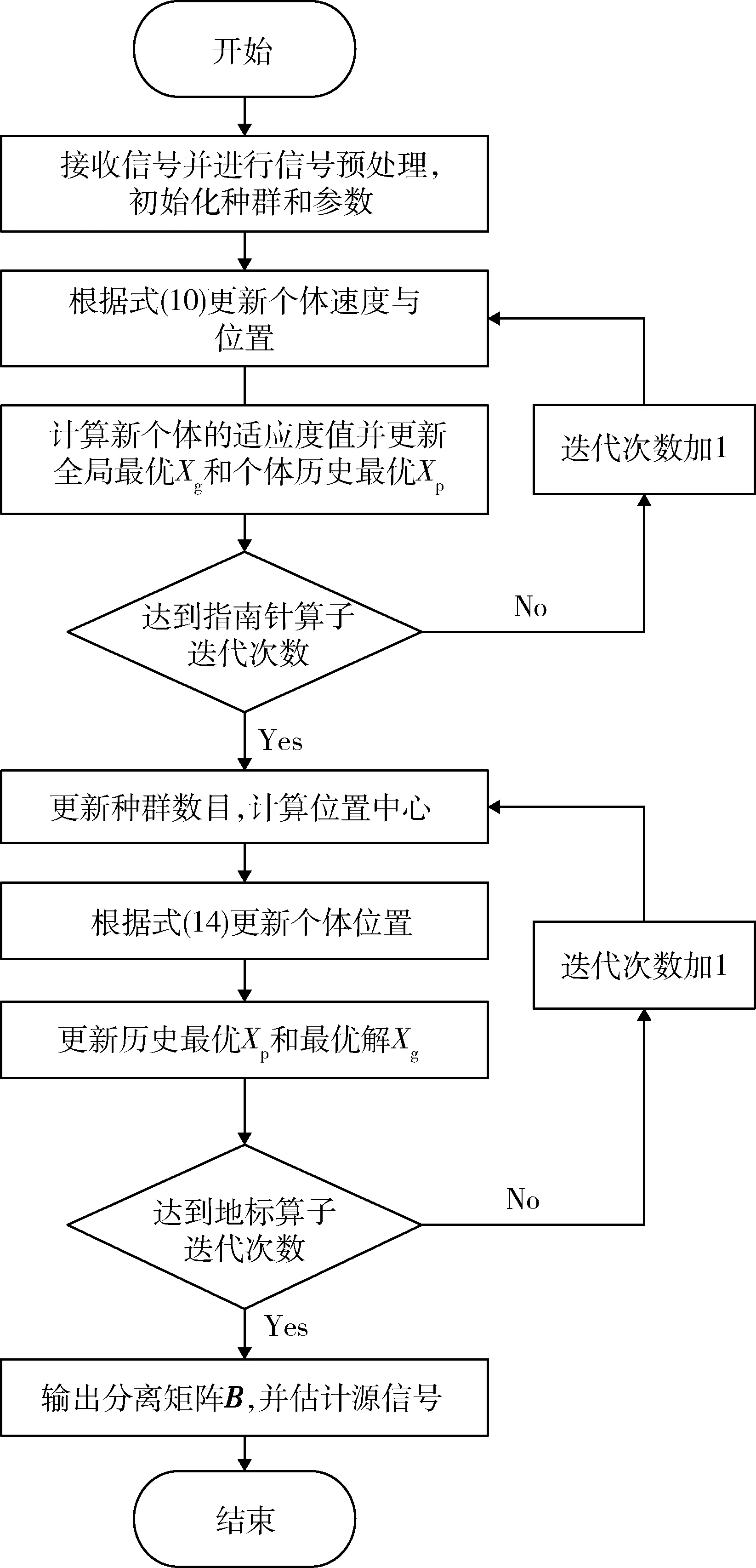
图 3 IPIO 算 法 流 程 图Fig. 3 Flowchart of IPIO algorithm

表 2 源信号名称及参数设置Table 2 Source signal name and parameter settings

取信号的时间长度都为20 μs，假设源信号同时到达，采样间隔0.01 μs，采样频率100 MHz，采样点数2 000，信号幅度均为1。假设接收通道为单个阵元，采用均匀线阵作为阵列模型。入射角度分别 为10°，20°，40°，70°，阵 元 间 距d设 为 波 长λ的1/2。

分别对比在上述参数设置下等变自适应盲源分离 （EASI）、标准鸽群算法（PIO）和改进鸽群算法（IPIO）的信号分离效果，如图4 所示。

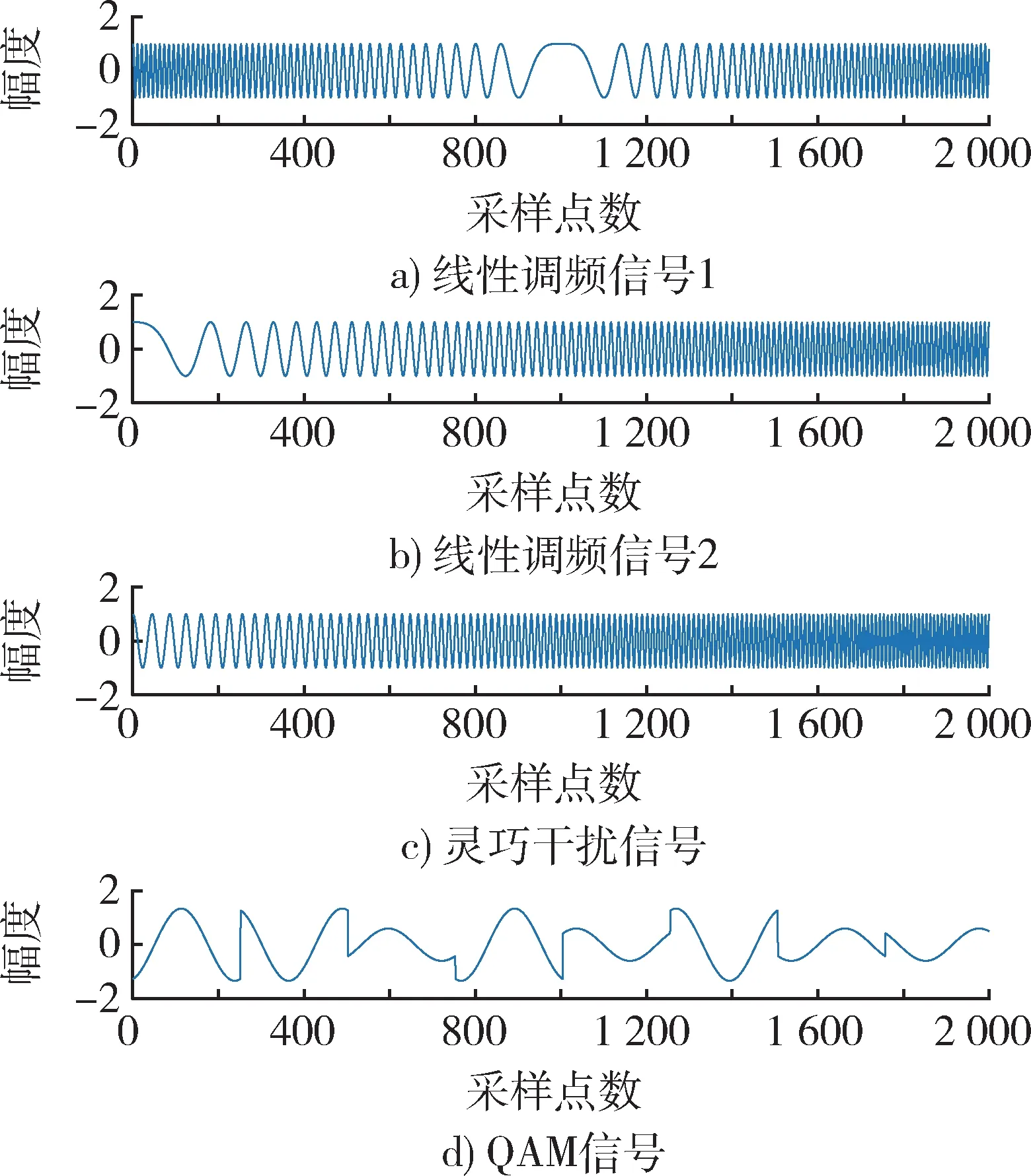
图 4 四路源信号波形图Fig. 4 Waveforms of four source signals

设最大迭代次数Max_iteration= 500，种群个数Np= 10，步长u= 0.01。

本文根据式（21）计算相似系数ζij，对分选性能进行定量评价

在上述公式中，源信号的真实值和估计值分别为si，yj，相似系数ζij的大小与1 越接近，则信号越相似。相似系数在0.9 以上时，说明算法具有较好的分选性能。同时，本文采用各个信号相似系数的平均值来衡量算法整体的分选效果。

4.1 低噪声情况

加入高斯白噪声，并将信噪比设为50 dB。观测结果如图5 所示。

图 5 低噪声情况下观测信号波形图Fig. 5 Observation signal waveforms under low noise

从图6～8 中分析可得，EASI 分选信号失真较为严重，PIO 分选信号也略有变形，IPIO 分选信号则与源信号几乎一致，分离效果较好。为了对3 种算法分离效果进行更加直观的对比，本文分别计算了3种算法的相似系数和收敛速度，并绘制了相似系数柱状图。结果如表3 和图9 所示。

从表3 和图9 的数据分析可以看出，在低噪声情况下，IPIO 算法对比EASI 算法和PIO 算法在各种信号的分离上有着更快的收敛速度，以及更高的分离精度，分离效果较为理想。

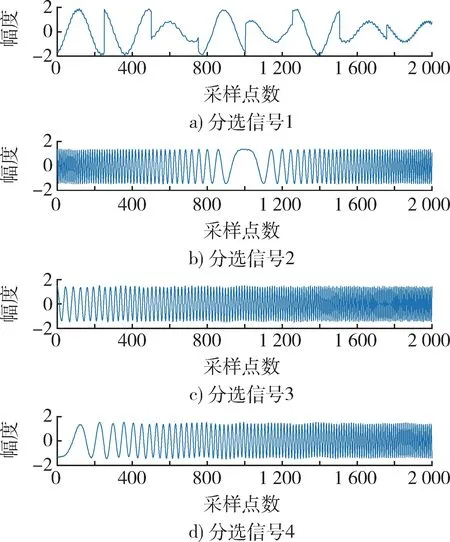
图 8 低噪声情况下的分选信号（IPIO 算法）Fig. 8 Sorted signal under low noise （IPIO algorithm）

4.2 高噪声情况

加入高斯白噪声，并将信噪比设为10 dB。

相比于低噪声情况，3 种方法在高噪声情况下分离性能均有所下降，但是由图10～12 可以看出，EASI 算法和PIO 算法分离出的信号失真现象已非常严重，而IPIO 则仅略有失真，与源信号吻合度较高。下面通过表格和绘制柱状图的方式进行具体数据分析。

表 3 低噪声情况下相似系数和迭代次数Table 3 Similarity coefficients and number of iterations under low noise

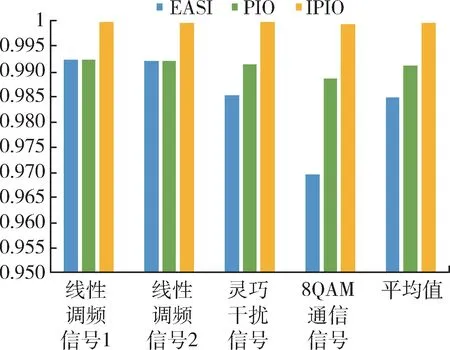
图 9 低噪声情况下相似系数柱状图Fig. 9 Histogram of similarity coefficients under low noise

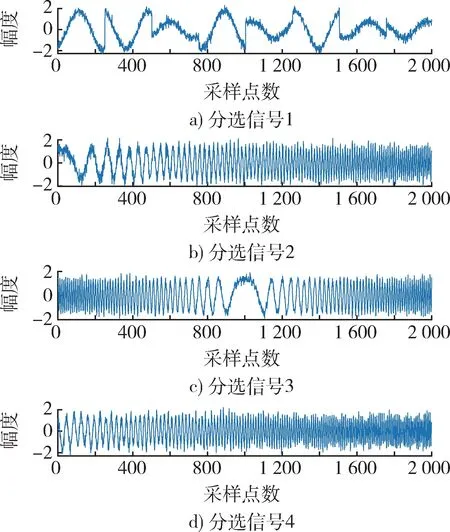
图 10 高噪声情况下分选信号（EASI）Fig. 10 Sorted signal under strong noise （EASI）

图 11 高噪声情况下分选信号（PIO）Fig. 11 Sorted signal under strong noise （PIO）

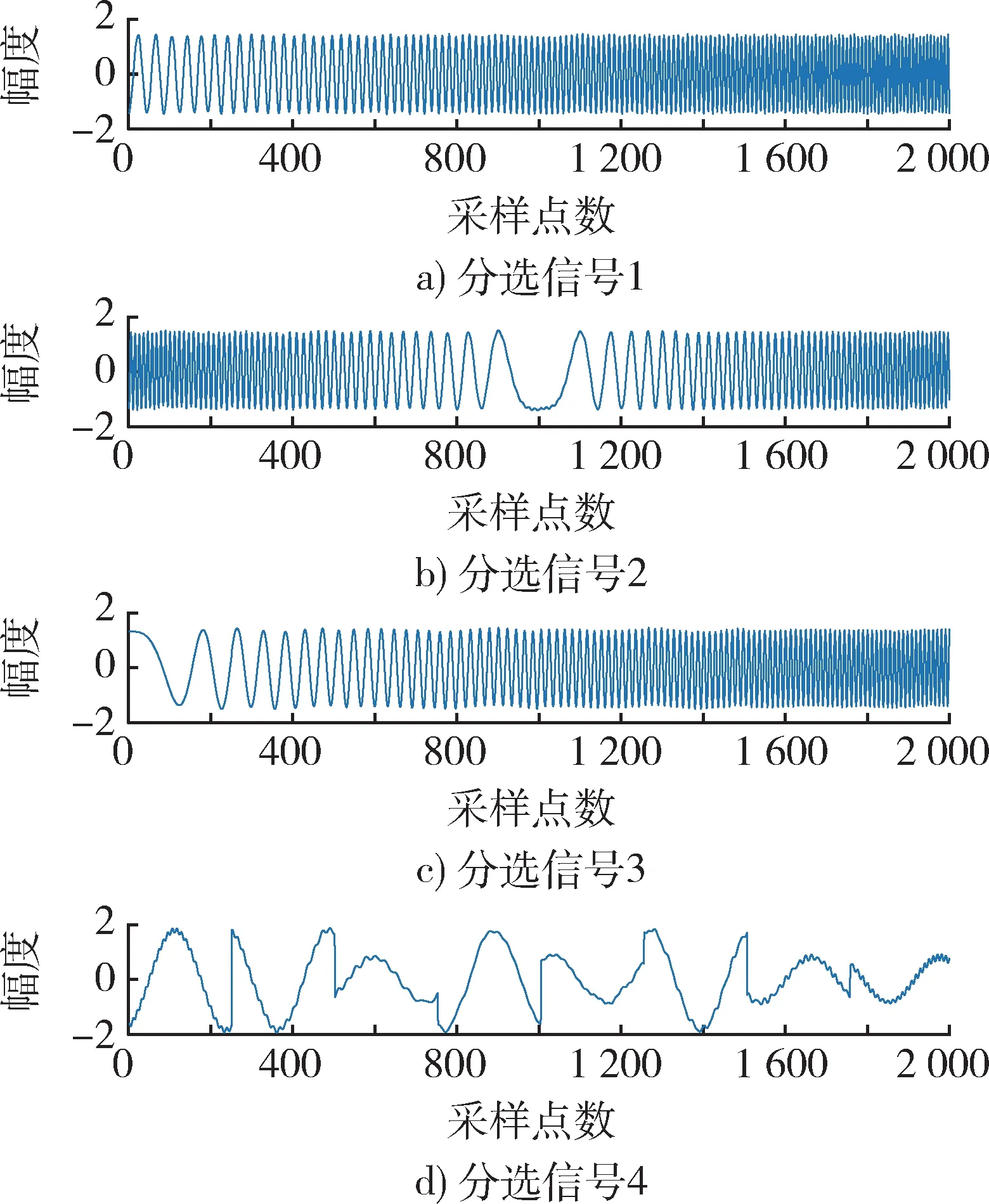
图 12 高噪声情况下分选信号（IPIO）Fig. 12 Sorted signal under strong noise （IPIO）

从表4 和图13 的数据分析可以看出，相比低噪声情况，在高噪声情况下，IPIO 算法对比EASI 算法和PIO 算法，在收敛速度、分离精度上具有更大的优势，分离效果十分理想。

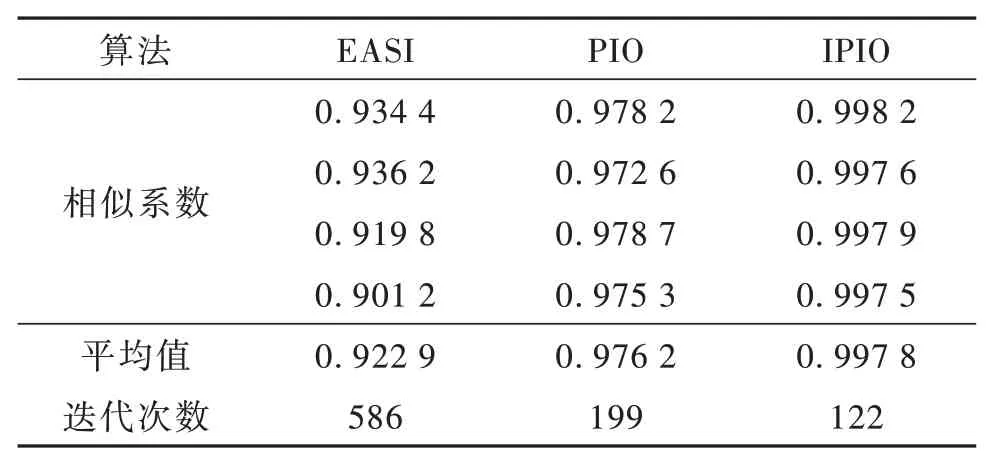
表4 高噪声情况下相似系数和迭代次数Table 4 Similarity coefficient and number of iterations under strong noise

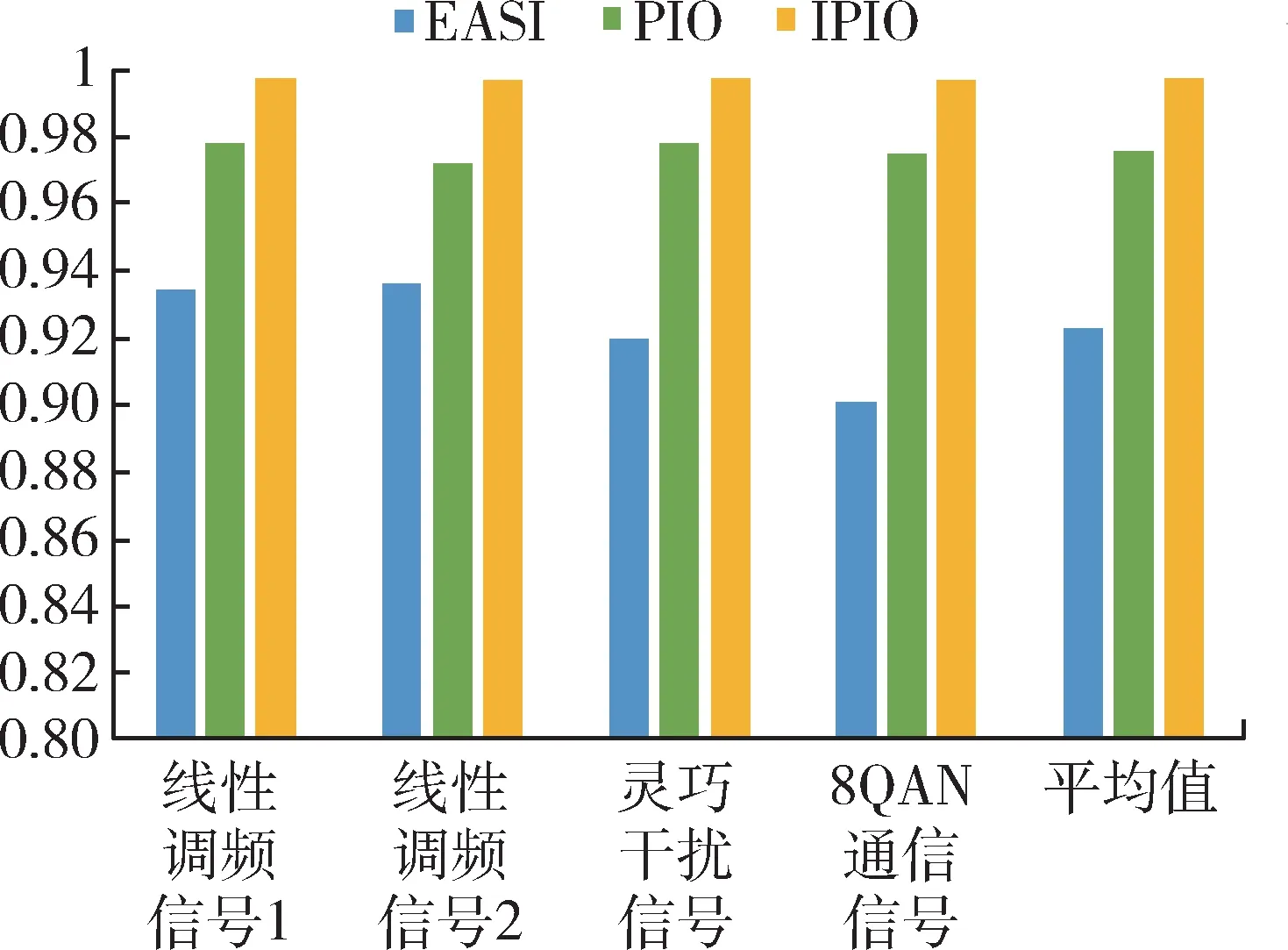
图 13 高噪声情况下相似系数柱状图Fig. 13 Histogram of similarity coefficients under strong noise

5 结束语

本文将位置因子和压缩因子引入鸽群算法，提出一种改进鸽群算法的复杂信号盲源分离方法，并在侦干探通一体化背景下进行信号分选，得到了不同环境下的仿真实验结果以及定量的性能分析。结果表明，对比标准鸽群算法和传统变步长自适应算法，本文提出的改进鸽群算法在低噪声条件下，分离精度和收敛速度上有一定提升，在高噪声条件下则有较大提升。总体来看，本文提出的算法有效提升了盲源信号分离性能。