基于“脱靶管”原理的防空导弹脱靶量估算方法 *

王激扬 ，白风宇 ，孙晓峰

（1. 海装北京局，北京 100073； 2. 中国人民解放军92493 部队，辽宁 葫芦岛 125001）

0 引言

防空导弹脱靶量是指导弹与目标交汇过程中的最小距离，是评估导弹武器系统制导精度等指标的重要依据，具体定义为：导弹在脱靶平面的落点与脱靶平面内目标连线的距离。而脱靶平面定义为：包含目标质点且垂直于导弹与目标相对速度矢量的平面［1］。

获取高精度脱靶量是评估导弹制导精度的关键，在实际飞行试验中，有2 种常用脱靶量获取方法：光学测量法和多普勒频率法。光学测量法，是采用光学设备，通过测量遭遇段导弹、目标位置参数获取脱靶量。但由于受到各种客观条件制约，一般难以直接测得防空导弹的脱靶量，即使测得导弹击落靶标时导弹爆炸时刻的弹目距离，从严格意义上来说也并不是真实的脱靶量。在具体工程实践中，一般采用测得导弹爆炸时刻的弹目距离来代替脱靶量的值，或利用遭遇段测得的一组导弹目标相对距离数据，通过插值、拟合、外推的方法得到粗略的脱靶量估值，精度较低，难以满足制导精度评估需求。多普勒频率法，是利用导弹无线电导引头或引信的多普勒信号进行处理估算脱靶量的方法，多种基于多普勒信号的脱靶量估算方法得到了广泛研究［2-15］。但这些算法成立的前提条件是弹目相对速度已知或能用导引头多普勒频率计算获得，由于不同防空导弹的制导体制不同，工程实际中时常不能满足该前提条件，算法应用受到制约。

本文提出了一种基于“脱靶管”原理的防空导弹脱靶量估算方法，分别针对光学测量数据和多普勒频率测量数据给出了具体的算法及算例。该算法不仅适用光学测量和多普勒测量2 种数据源，也适用弹目相对速度未知条件下的脱靶量计算，具有简便快捷、计算精度高、工程实用性好等特点。

1 “脱靶管”原理

地（舰）空等防空导弹拦截试验中，在导弹目标交汇“瞬间”如（0～0.3 s）内的遭遇段，相对速度矢量vr的大小和方向是不变的。因此，根据脱靶量及脱靶平面的定义，导弹相对目标运动的总和就形成一个空心圆柱的“脱靶管”，其轴平行于相对速度矢量，在空心圆柱表面上依次是脱靶相位φ、脱靶量值ρ和相对速度矢量vr，脱靶量是从“停止导弹”向相对速度矢量的垂线，如图1 a）所示。由“脱靶管”的描述可知，在弹目交汇形成的脱靶管中，脱靶相位φ、相对速度vr和脱靶量ρ的大小、方向均保持不变，这给脱靶量的计算带来较大的便利。在实际应用中，采用脱靶管截面的平面图更为简便直观，且不影响计算结果，如图1 b）所示。

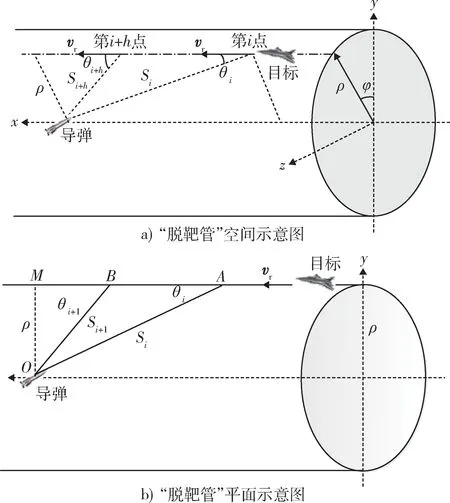
图1 “脱靶管”原理示意图Fig. 1 Principle of “miss distance tube”

2 基于外弹道测量数据的脱靶量计算

由图1 b）所示，对于导弹目标交汇段，通过外弹道光学测量并经数据处理，可直接得到发射坐标系下导弹在第i点处的坐标、目标在第i点处的坐标和第i点弹目相对距离Si；同样，对于第i+1 点可得到：，Si+1；其中，i=1，2，…，n。

设第i点至第i+1 点目标相对导弹的运动距离为Di，其计算公式如下：

对于图1b）中三角形，应用余弦定理可计算确定θi+1，θi：

因此脱靶量ρ的估计值为

一般对于遭遇段密集的n个测量点，可以选择适当的计算步长，即通过选择i与i+1 点的时间间隔Δt来实现，可得到一组脱靶量的估计，经过平滑处理，剔除野值，取平均得到最终的脱靶量估计值。

假设某型地空导弹飞行试验遭遇段一组外弹道测量数据如表1，其中（XM，YM，ZM）为导弹坐标值，（XT，YT，ZT）为目标坐标值，dR为弹目相对距离；对应上述给出的计算公式，导弹坐标、目标 坐 标、弹 目 相 对 距 离Si，i=1，2，…，13。

表1 脱靶量光学测量结果Table 1 Optical measurement results of miss distance

利用表1 数据计算导弹脱靶量，具体步骤如下：

（1） 选择计算步长Δt，若选取Δt=0.01 s，对应表1 的13 组测量数据，得到一组10 个脱靶量的估计值。

（2） 按式（1）计算第i点和第i+1 点的目标相对导弹的运动距离Di；按式（2）计算θi+1或θi角度值；按式（3）计算得到脱靶量ρi。

（3） 对于计算得到的一组脱靶量ρi（i=1，2，…，10），剔除野值，并取平均得到该次飞行试验导弹脱靶量为0.84 m。

对于表1 数据，采用传统拟合外推方法，得到的弹目距离拟合曲线近似直线，外推脱靶量值为0；利用不精确炸点时刻测量值（炸点时刻测量误差为±0.002 s），外推估算得到导弹爆炸时刻弹目最小距离值在5.476～1.224 m 之间，具体脱靶量值难以确定。由此看出，基于“脱靶管”原理的脱靶量计算方法，可在非精确测量条件下，得到较高精度的脱靶量的值，是光学测量数据估算脱靶量的有效手段。

3 基于遥测多普勒频率信号的脱靶量计算

对于导引头或引信存在多普勒频率信息的导弹飞行试验，通过遥测可获得弹目交汇段的多普勒频率信号，通过选取间隔时间Δt，得到一组变化的多普勒频率fdi，i=1，2，…，n；如图2 所示，多普勒频率fdi计算公式：

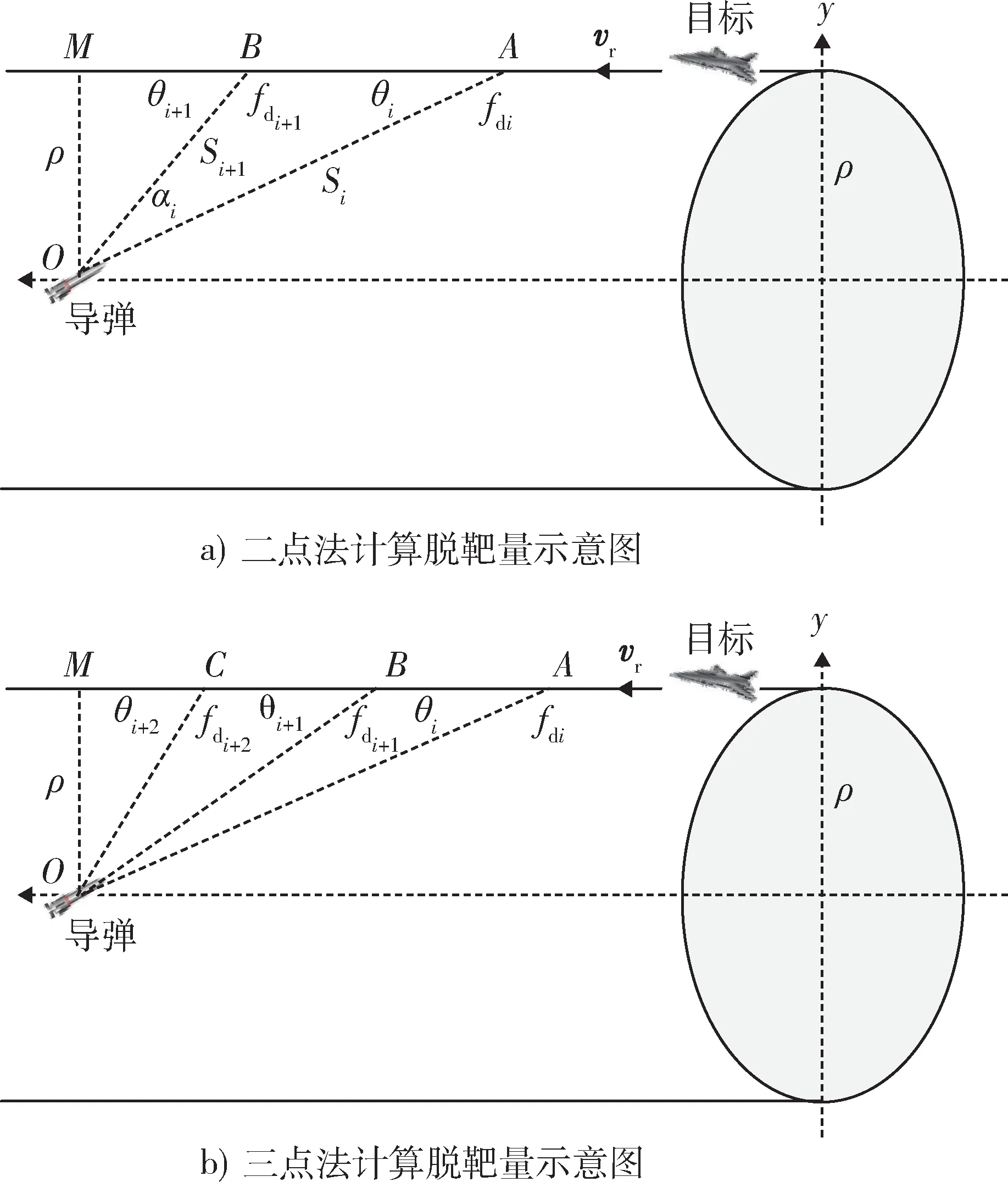
图2 基于多普勒频率的“脱靶管”原理示意图Fig. 2 Principle of “miss distance tube” based on Doppler frequency

一般地，当弹目距离S≥（200～300） m时，θi≈0，cosθi≈1，则可通过此时测得多普勒频率由式（4）计算得到相对速度vr（仍不够精确）；否则，相对速度vr未知。

3.1 相对速度vr已知情况

相对速度vr已知时，脱靶量计算较为简单，可采用“两点法”计算脱靶量，如图2 a）所示，选取间隔Δt的 两 点 普 勒 频 率 值fdi，fdi+1；对 应 角 度θi，θi+1，由 式（4）计算得到：

由于α=θi+1-θi，应用三角形正弦定理，有

则可直接得到脱靶量估计为

这样可得到一组脱靶量ρ的估计：ρ1，ρ2，…，ρi，通过平滑、剔除野值、取平均等处理，能够得到较高精度的脱靶量估计。

3.2 相对速度vr未知情况

当相对速度vr未知时，根据测得的多普勒频率，首先求得相对速度vr，之后应用式（6）即可得到一组脱靶量ρ的估计。

采用“三点”法求解相对速度vr，如图2 b）所示，选 取 等 时 间 间 隔Δt的 三 点 普 勒 频 率 值fdi，fdi+1，fdi+2，有对应角θi，θi+1，θi+2；由于AB=BC，则有：

将式（4）变换为三角函数代入上式，整理后有

函数F(vr)（或|F(vr)|）的零点就是要求解的相对速度，可采用二分法迭代算法或黄金分割迭代算法（只适用|F(vr)|）求解［9］。

3.3 示例计算

假定某型导弹某次飞行试验中弹目交汇段等间隔时间提取一组多普勒频率数据，经拟合平滑后，得到数据如表2 所示。

表2 导弹飞行试验交汇段多普勒频率数据表Table 2 Doppler frequency data for intersection section in missile flight test

（1） 采用“三点法”求解相对速度vr

假设弹目速度未知，根据交汇段弹目速度估算，给 出 弹 目 相 对 速 度 范 围 ：vr∈(a，b) =(vrmin，2 000)，其中vrmin为使函数F（vr）有意义的取值，满足

式中：max（）为求最大值。

若取时间间隔Δt=0.004 s，采用二分法计算导弹与目标相对速度vr，计算取值及计算结果见表3，其中以序号2 的一组数据为例的函数F（vr）图像如图3 所示，对应的零点为vr=1 129 m/s。

表3 采用拟合多普勒频率计算的导弹目标相对速度和脱靶量计算结果Table 3 Results of relative velocity and miss distance calculated by fitting Doppler frequency

图3 函数F(vr)曲线图Fig. 3 Curve of function F（vr）

（2） 采用“二点法”计算脱靶量ρ

依据表2 数据，在求得相对速度vr后，根据式（5），（6）计算脱靶量ρ，可得到一组脱靶量的值，取平均后即为最终获取的脱靶量值ρ=10.05 m。计算结果如表3。

（3） 计算精度分析

需要指出的是，表2 数据取自某专项试验脱靶量为10 m 时的引信多普勒频率拟合曲线［2］，脱靶量真值已知：ρ=10 m。由于引信对目标体不同散射点的多普勒频率值具有一定的散布误差，也存在测量的随机误差，虽然经过拟合平滑，却难以根本消除。因此，表3 中计算得到的一组脱靶量值同样具有一定的离散，其均方根误差σ=0.53 m，但取平均后，可有效消除随机误差，获得较高精度的脱靶量值。本例计算得到的脱靶量值10.05 m 与真值相差甚微，精度达到99.5%，表明基于“脱靶管”原理的脱靶量估算方法具有明显优势，并较好地解决了弹目相对速度未知情况的脱靶量估算问题。

4 结束语

本文针对防空导弹飞行试验精确脱靶量获取困难实际问题，提出了一种基于“脱靶管”原理的脱靶量估算方法。分别针对光学位置测量和内弹道遥测多普勒频率测量的不同数据源情况，给出了脱靶量估算算法，较好解决了非精确光学测量条件和利用多普勒频率弹目相对速度未知条件下的脱靶量估算问题。应用示例表明，该方法精度高，应用广泛，具有较高的工程应用价值。