超平面交单调锥上投影算子的快速算法及其实现
2023-05-30刘勇进汤婉红
刘勇进,汤婉红
(福州大学数学与统计学院,福建 福州 350108)
0 引言

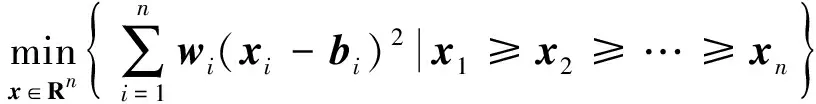
其中,xi∈R,i=1,…,n表示向量x∈Rn中的第i项分量.保序回归问题在统计、数学规划、生产计划和库存控制等领域具有重要的实际应用.具体地,保序回归问题应用于分类器、广告排序和质量控制等等实际问题.由于保序回归问题没有考虑到估计量所在空间的已知信息.在估计量中加入先验信息可以带来更好的估计性能,一般的方法是在该估计量上添加一个线性约束[2],常见的例子包括非负最小二乘回归[3],保序回归[1]等.基于以上背景,考虑在保序回归问题上添加一个线性约束,即对于给定向量b∈Rn和τ>0,考虑以下优化问题,即

(1)
其中,en表示分量全为1的n维列向量.可以观察到问题(1)的最优解是b在超平面交单调锥上的投影.
目前国内外的学者设计了各种有效的算法求解保序回归问题,主要包括: Van Eeden算法[4]、最小下集算法(minimum lower sets,MLS)[5]、池相邻违反算法(pool adjacent violators,PAV)[4]等.但是求解超平面交单调锥上的投影问题(1)的算法比较少,所以设计求解问题(1)的有效算法是必要的.在文献[6]中,求解有序加权l1范数投影问题[7]可以转变为求解如下优化问题,即
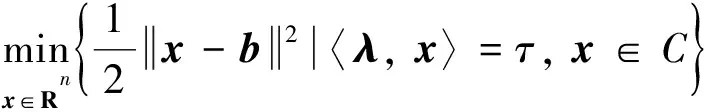
(2)
其中:λ∈Rn,λ中的分量不全为0且满足λ1≥λ2≥…≥λn≥0和集合C={x∈Rn|x1≥x2≥…≥xn≥0,x≠0}.
Li等[7]通过随机数据集上的数值实验表明了半光滑牛顿算法可以有效地求解问题(2)的对偶问题.由于问题(1)和问题(2)的形式相似,所以考虑用半光滑牛顿法求解问题(1)的KKT系统.此外,在文献[8]中,PAV算法能够高效地求解保序回归问题,所以也考虑用PAV算法求解问题(1)[9].
主要研究在超平面交单调锥上的投影问题.首先,介绍一些相关的预备知识;接着,给出求解该问题的PAV法和半光滑牛顿法并分析算法的有效性;最后,根据两种算法的数值结果验证: 在求解随机数据集上的投影问题时,PAV算法比半光滑牛顿算法更高效.
1 PAV算法
1.1 问题描述
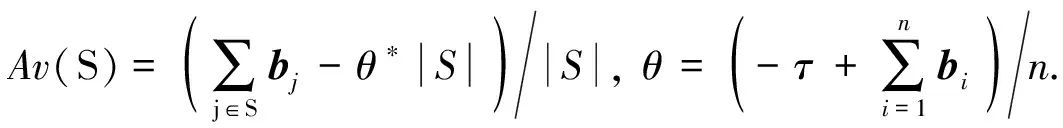
Av(S)=(W(Li)Av(Li)+W(Ui)Av(Ui))/W(S) (i∈S)
(3)
其中:σ∈R是问题(1)中等式约束对应的拉格朗日乘子,v∈Rn-1是问题(1)中不等式约束对应的拉格朗日乘子.问题(1)的KKT条件为
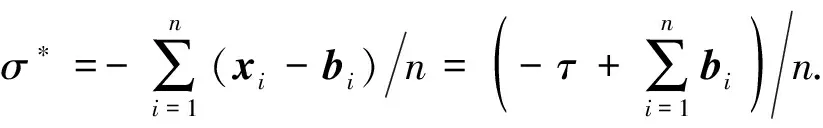
有效集J的KKT系统的解可以通过求解有效集J的每个分块相应的子系统来获得.定义对应于有效集J的KKT系统的解为拟稳定点.下面的定理提供了KKT子系统解的显式公式.
定理1方程组(4)的解为:xi=Av(B),i∈B和vi可以从以下3个等价表达式中的任意一个获得,即
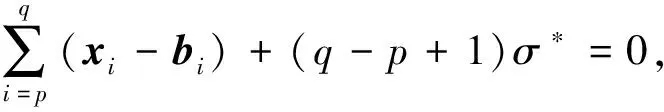
下面用数学归纳法证明定理的第二个结果.当i=p时,由(4a)得:vp=W(Lp)(Av(B)-Av(Lp));假设p≤i-1 vi=xi-bi+σ*+vi-1=(Av(B)-(bi-σ*))+W(Li-1)(Av(B)-Av(Li-1))=W(Li)(Av(B)-Av(Li)) 综上可知,(5a)第一个等式成立.另外,(5a)第二个等式和(5b)可由(5a)第一个等式和式(3)得到.证毕. 由定理1以及原始和对偶可行性的定义可得下述推论. 推论1令J是一个有效集,B是有效集J的一个分块.拟稳定点是原始可行的当且仅当对任意满足B-≠Ø的分块B,Av(B-)≥Av(B)成立.拟稳定点是对偶可行的当且仅当对∀i∈B以下3个等价条件每一个条件都成立: Av(B)≥Av(Li),Av(Ui)≥Av(B),Av(Ui)≥Av(Li) (6) 下面给出PAV法求解问题(1)的算法迭代框架. 算法1: PAV算法输入: 令J={{1}, {2}, …, {n}}, B0={1}.1: if B+=Ø, then终止算法, 输出xi=Av(B),i∈B,B⊆J.2: else3: if Av(B0)≥Av(B+), B0=B+; 转步骤1;4: else5: J=J{B0, B+}∪{B0∪B+}, B0=B0∪B+. 6: while B-≠Ø&&Av(B-) 下面给出用于建立PAV算法有效性的引理. 接下来介绍PAV算法求解问题(1)的有效性定理. 定理2PAV算法在有限步内得到问题(1)的最优解,且算法复杂度为O(n). 证明: 由PAV算法的描述可知,算法终止时获得的有效集对应的拟稳定是原始可行的.下面用数学归纳法证明PAV算法每一次产生的拟稳定点均是对偶可行的.PAV算法第一次执行时,拟稳定点满足对偶可行.假设第k次执行时,拟稳定点是对偶可行的.则第k+1次执行时,如果Av(B0)≥Av(B+),根据假设,此时拟稳定点仍是对偶可行的;如果Av(B0) 半光滑牛顿算法是目前用于求解中等规模或大规模的优化问题最有效的求解方法之一,其收敛速度是超线性收敛甚至可达到二次收敛.本节主要介绍半光滑牛顿算法求解问题(1)的详细过程. 令矩阵G∈R(n-1)×n满足 Gx=[x1-x2,x2-x3,…,xn-1-xn]T(∀x∈Rn) 那么,问题(1)等价于 (7) 问题(7)的拉格朗日函数为 (8) 由方程组(8)可以得到最优拉格朗日乘子σ*为 (9) 求解问题(7)转变为求解下述非线性方程组: (10) F(y)=0 (11) J(y)=I-W(I-GGT) 下面给出关于雅可比矩阵J(y)的一些性质. 证明: 令[n-1]={1,2,…,n-1}.由于当i∈C0且Wi,i取值为0或1时,可以把指标i视作其属于指标集C-或C+的情形考虑,因此当i∈C0时,以下证明只考虑Wi,i取值为(0,1)区间任一数值的情形. 情形1 当C+=[n-1]时,J(y)=I-W(I-GGT)=GGT.由于det(J(y))=det(GGT)=n≠0,所以,雅可比矩阵J(y)是非奇异的. 情形2 当C-=[n-1]时,J(y)=I.由于det(J(y))=det(I)=1≠0,所以,雅可比矩阵J(y)是非奇异的. 情形3 当C0=[n-1]时,J(y)=I-W(I-GGT)为严格对角占优矩阵,所以,雅可比矩阵J(y)是非奇异的. 情形4 当C+=Ø,C0和C-都不为[n-1]时,J(y)为严格对角占优矩阵,所以,雅可比矩阵J(y)是非奇异的. 情形5 当C0=Ø,C+和C-都不为[n-1]时,令s∈R(n-1),构造齐次线性方程组为 (I-W(I-GGT))s=0 (12) 要证明雅可比矩阵J(y)是非奇异的,只需证明方程组(12)的解s为零向量.对式(12)进行初等变换可得 ?匌 (13) 情形6 当C-=Ø,C+和C0都不为[n-1]时,雅可比矩阵J(y)为三对角阵.通过一系列初等行列式变化使得矩阵J(y)上下两条次对角线都为-1,即 从最后一列展开得:Dn-1=an-1Dn-2-Dn-3.而D1=a1>0;D2=a1a2-1>0;由于D2-D1=(a2-1)a1-1≥a1-1>0,所以D3=a3D2-D1≥2D2-D1>0;由于D3-D2=(a3D2-D1)-D2=(a3-1)D2-D1≥D2-D1>0,所以D4=a4D3-D2≥2D3-D2>0;由于D4-D3=(a4D3-D2)-D3≥D3-D2>0;所以D5=a5D4-D3≥2D4-D3>0;…;Dn-1=an-1Dn-2-Dn-3≥2Dn-2-Dn-3>0.由上述可知,det(J(y))≠0.所以,雅可比矩阵J(y)是非奇异的. 情形7 当C-,C+和C0都不为[n-1]时,由情形6可知,当C-=Ø,C+和C0都不为[n-1]时,雅可比矩阵J(y)的行向量组线性无关.再结合情形5的证明思路,即可证明命题.证毕. 下面给出当i∈C0,Wi,i=0时,雅克比矩阵J(y)的LU分解. 证明: 令L,U∈R(n-1)×(n-1),L是主对角元全为1的下三角矩阵,U是上三角矩阵,使得 J(y)=I-W(I-GGT)=LU 成立.由于J(y)是三对角矩阵,通过计算可知: 矩阵U满足Ui,j=0,j-i>1和矩阵L满足Li,j=0,i-j>1.下面给出矩阵L和矩阵U其余元素值.具体地,令p∈Rn-1,若i∈C+,pi=1,否则pi=0.p可划分成N个子向量,这些子向量要么是全1向量要么是零向量,并且任意两个相邻子向量是不同的,即 最后,给出矩阵U主对角线上一行元素的值: 若i∈C+,Ui,i+1=-1,否则Ui,i+1=0,i=1,…,n-2. 由于雅可比矩阵J(y)是非奇异且存在LU分解,从而得出雅可比矩阵J(y)的LU分解唯一的.证毕. 由命题2知,雅可比矩阵J(y)可以被分解成矩阵L和矩阵U的乘积,因此可以利用这两个稀疏矩阵通过下面步骤获得牛顿方向,即:Uz=-F,Ud=z.其中,z∈Rn-1是一个临时变量.经过运算可得:Uz=-F,Ud=z.其中:z∈Rn-1是一个临时变量.通过计算可得 z1=-F1,zi=-Fi-Li,i-1zi-1(i=2,…,n-1) (14) 因此,牛顿迭代方向为 (15) 下面给出半光滑牛顿法求解问题(7)的算法框架. 算法2: 半光滑牛顿算法(SSN)输入: b∈Rn, y0∈Rn-1+, ω∈(0, 0.5), μ∈(0, 1), ε>0, t=0.1: whileF(yt)>ε do2: 通过式(14)~(15)计算dt;3: 令ξt=ωmt, 其中mt为满足下面条件的最小非负整数m:F(yt+ωmdt)2≤F(yt)2-2μωmF(yt)2.4: yt+1=yt+ξtdt; t=t+1;5: end while;6: 通过式(9)计算σ∗;7: 输出x=b+σ∗en+GTy. 由文献[12]中定理3.2和文献[13]中定理2.4可得下述定理成立. 定理3若{yk}是由算法2生成的序列,则{yk}收敛到问题(7)的最优解y*,且收敛速度是二阶的. 表1 当δ=10-3时,PAV,SSN 算法在随机数据集上的实验结果 表2 当δ=1时,PAV,SSN 算法在随机数据集上的实验结果 针对问题(1),充分利用 KKT 最优性理论条件,给出求解该问题的PAV法和半光滑牛顿法并对算法进行了有效性分析,最后通过大量的数值实验证明了在求解随机数据集上的投影问题(1)时,PAV算法比半光滑牛顿算法更高效.然而,PAV法不能推广应用于求解问题(2),而半光滑牛顿算法仍可用于求解问题(2).1.2 PAV法的算法框架和有效性


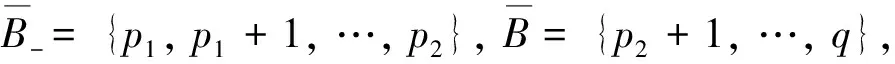
2 半光滑牛顿法
2.1 问题重构





2.2 半光滑牛顿方向的求解

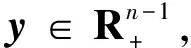
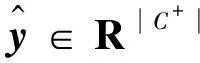
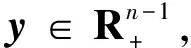

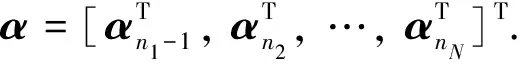

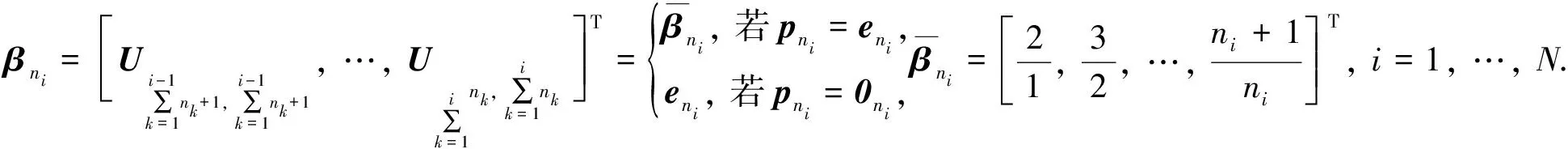

2.3 半光滑牛顿法的算法框架和收敛性

3 数值实验与结果分析



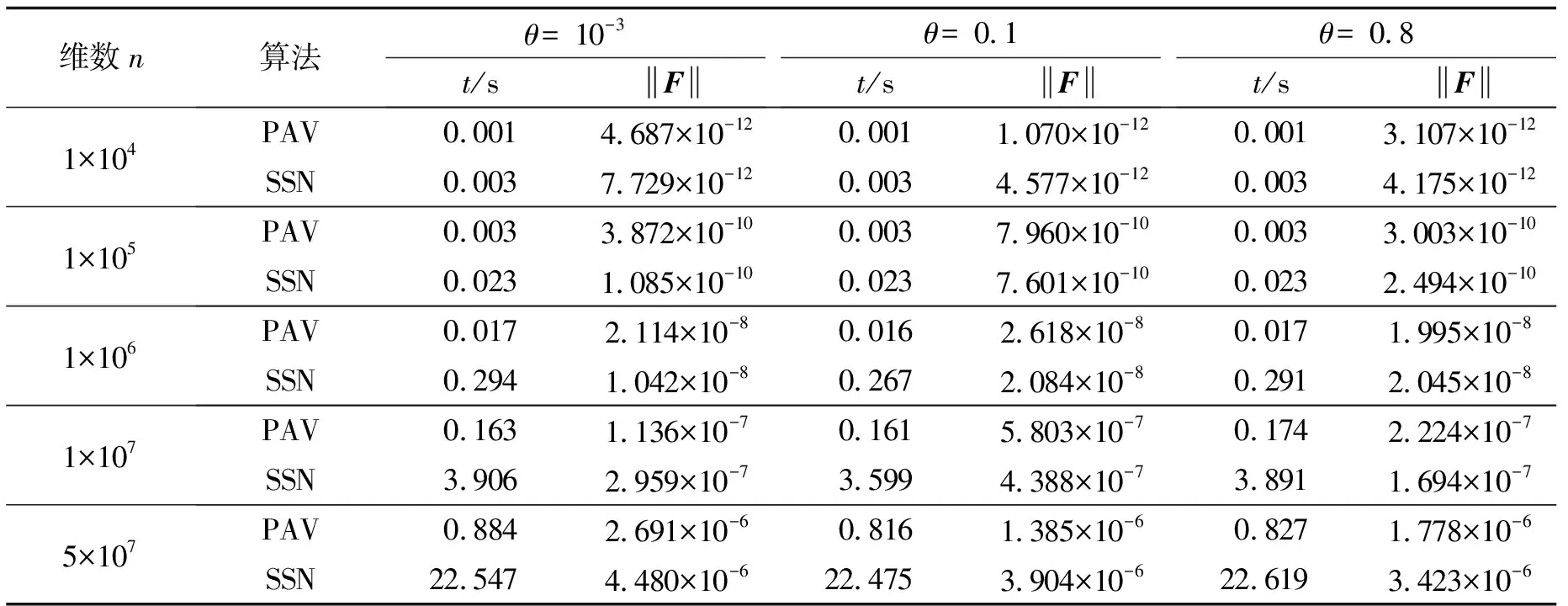
4 结语
