地铁隧道列车循环荷载下粉砂地基长期沉降研究

朱 颖, 钱晓华, 曾长女, 赵金兴, 易领兵

(1.郑州地铁集团有限公司,河南 郑州 450000; 2.上海隧道工程有限公司,上海 200232; 3.河南工业大学 土木建筑学院,河南 郑州 450001; 4.黄河勘测规划设计研究院有限公司,河南 郑州 450003)

地铁隧道大多集中于城市内,地铁线路设计受限制较多,曲线隧道常常不可避免,由于各种条件影响,有时还会产生小半径曲线隧道,土体类型、曲线隧道不同曲率、列车速度等对地铁隧道地基长期变形的影响不容忽略。已运营多年的郑州轨道交通1号线,有多段曲线隧道及小半径曲线隧道段,某段曲率半径为350 m的隧道地基最大变形达40 mm,这类地段地基的长期变形问题是运营维护的重点工作。隧道地基长期处于列车振动荷载作用下,随着运营时间不断增加,引起的地基塑性变形不断累积,当地基变形达到设计允许最大值后,隧道地基使用功能降低,容易造成更大的沉降;此外,受地下水影响,地基土体可能因列车振动荷载导致孔隙水压力上升,且不易完全消散,孔压不断累积,可能使土体液化丧失强度或产生过大变形,甚至威胁列车运行安全。郑州处于黄河中下游地区,地层中的粉细砂土分布广泛,这类粉砂土有液化可能性,可能发生较大的累积变形,有必要研究该地区粉砂土地基累积变形发展规律,为地铁安全运营提供保障。

对于振动荷载下各类土体产生的累积变形,相关研究成果较丰富,涉及软黏土[1-5]、黄土[6]、粉土[7]、黏土与粉土复合地层[8]、珊瑚砂[9]、泥炭质土[10]和土石混合体回填土[11]、重金属污染膨胀土[12]等不同的土类。针对饱和软土,文献[13]研究其累积变形特性,分析振动次数、列车频率、动应力幅值、固结比、排水条件等因素对其的影响规律。针对软黏土,文献[1]建立不同影响因素下应变的软化模型;文献[2]用对数关系曲线描述残余应变与振动圈数的影响规律;文献[3]设计正交试验,研究不同因素对饱和软黏土累积变形的影响率及评价方法;文献[4]通过拟合得到沉降预测模型所需参数,采用分层总和法预测地铁隧道的长期沉降。文献[6]以西安地铁2号线为研究实例,建立列车-轨道-地基系统分析模型,并采用数值分析讨论黄土地区地铁荷载影响下地表振动的响应规律;文献[7]采用连续循环加载和间歇加载动力试验,对粉土间歇阶段的累积塑性应变和轴向应变等发展规律进行研究,得到粉土试样临界应力的表达式和累积塑性应变预测模型;文献[14]研究砂土在不同主应力系数下轴向、径向、环向的动应变随振次的发展趋势;文献[15]利用分数阶导数推导累积剪切应变与加载周期之间的幂律关系,较好地捕捉到不同加载条件下剪切应变与相应加载周期之间的幂律演化规律;文献[16]得到小半径曲线隧道盾构施工时曲率半径越大,周边土体的地表沉降越小,该研究主要针对施工期的影响;文献[17]研究的曲线隧道曲率相对较大,但未对更大曲率范围的曲线隧道进行研究。

本文以已运营的郑州轨道交通1号线一期工程为工程实例,研究不同曲率曲线隧道,尤其是小半径曲线隧道地铁长期运行下的路基长期沉降规律;考虑黄泛区粉砂土特点,设计大振次粉砂土动三轴试验,获取其塑性长期累积变形曲线,提出长期累积变形预测模型;结合该实际工程,根据地铁未来的发展,在隧道曲率半径变化区间为250～350 m、列车运行速度变化为40～200 km/h下,考虑列车动荷载、小曲率半径、列车荷载等对地层变形的影响,建立曲线地铁隧道三维有限元模型,通过数值计算获取不同地层在列车经过时的地层动应力,结合长期累积变形预测模型,研究不同曲率半径、不同列车速度对地层长期累积变形的影响规律,以期为类似曲线地铁隧道设计和运营提供理论参考。

1 地铁循环荷载下粉砂土累积变形特征

1.1 试验方案

试验用土取自郑州轨道交通1号线农业南路站—东风南路站盾构区埋深15～20 m的粉砂土,土样的基本物理力学性质指标如下。

(1) 3种粒径下粉砂土颗粒的质量分数分别为:0.50～0.25 mm,10.37%;0.250～0.075 mm,47.09%;小于0.075 mm,42.54%。

(2) 含水率为23.54%,密度为1.64 g/cm3,最大孔隙比为0.93,最小孔隙比为0.51。

采用英国GDS Instruments公司生产的动态三轴测试系统,如图1所示。试样制作与加载过程图片如图2所示。采用三瓣模安装试样以减少对试样的扰动,将橡皮膜贴合在三瓣模上,橡皮膜下端用橡皮筋扎紧,将固定质量的粉砂土分3次均匀倒入橡皮膜内,装样过程中对试样进行适度振捣以避免分层,最后制备出圆柱体重塑试样,试样尺寸(直径×高度)为50 mm×100 mm。试验具体步骤如下:

图1 动态三轴测试系统图片

图2 试样制作与加载图片

(1) 压力室充水后先输入20 kPa围压稳定试样,然后进行CO2饱和:① 从下部反压接口通入CO2,同时打开上反压排气阀门,用CO2置换试样中的空气,直至出口处未见气泡排出;② 从下部反压接口通入无气水,使试样中CO2溶于水;③ 施加反压,提升饱和度,直至饱和度达98%以上。

(2) 输入围压目标值对试样进行固结,固结完成后根据试验方案对试样进行剪切。

试验考虑以下3种影响因素:① 有效固结应力p′,考虑不同隧道埋深影响,p′选用100、200、300 kPa;② 动应力幅值qd,考虑列车及隧道体系施加在小曲率半径曲线隧道道床底部的附加应力在20～40 kPa之间,试验采用qd分别为20、30、40 kPa;③ 荷载频率f,考虑地铁运行所产生的振动频率对地基的影响区间,根据郑州地铁动荷载的优势频率和工程场地地震安全性评价中场地的动力特性试验常用频率,取f分别为0.5、1.0、2.5 Hz,对应列车速度分别为40、80、200 km/h。

当地铁运行时,土体产生压缩变形,试验采用半正弦函数作为轴向动循环荷载的典型波形;由于地铁列车动力响应波形有循环往复的特点,试验采用应力控制循环加载模式,采用半正弦波形荷载进行荷载施加,并进行大振次的振动循环试验,设定试验循环周数(N)为5 000圈。典型轴向循环荷载波形如图3所示。

图3 典型轴向循环荷载波形

具体累积变形试验方案见表1所列,每个试样均进行2次重复,确保试验结果可重复。

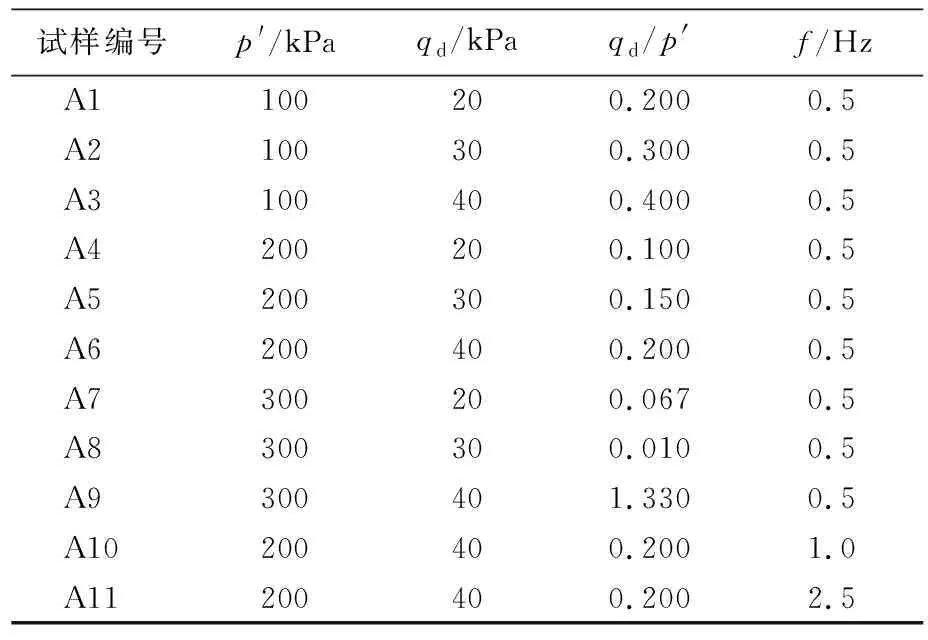
表1 累积变形试验方案

1.2 累积变形计算

受地铁循环荷载作用,粉砂土轴向应变εd具有周期性,由弹性和塑性应变共同构成。在1个循环周期内,当动应力值达到最大,最大弹性应变和塑性应变之和为最大主应变εq,即轴向应变每圈的峰值;当动应力值全部卸载后,弹性应变消失,不可恢复的变形为塑性变形,即轴向应变每圈的阈值,也称为残余应变εp。本文考虑εp的发展规律。

3种影响因素下εp的变化曲线如图4所示。由图4可知,在试验范围内该粉砂土残余变形发展可分为3个阶段:第1阶段为荷载作用初期,应变呈类似线性发展的增长趋势;第2阶段为一定振动循环周数后,应变仍持续增长,但发展速率变缓;第3阶段为循环周数达到较大值后,应变增长速率进一步减缓,应变值趋于稳定。与文献[2-3]中的软黏土累积变形规律相比,虽然软黏土也经历了上述3个阶段,但第1阶段粉砂土的应变增长速率要比软黏土的应变速率快,第1阶段初期产生的变形量更大,故地铁运行初期该粉砂土更易受到振动变形破坏;且由图4c可知,低频率荷载为主要危害源,这是由于当其他的影响因素不变时,荷载频率越低,其变化速率越慢,作用时间变长,对土体输入的总能量就越多,土体的变形就越大。

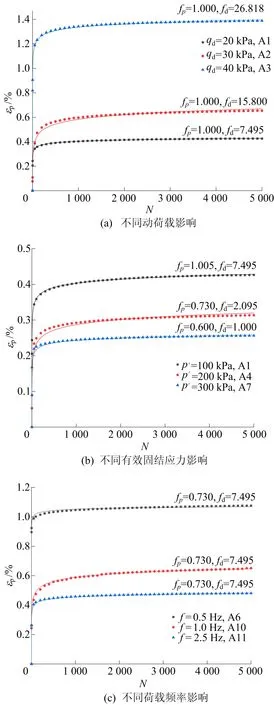
图4 3种影响因素下的εp变化曲线

针对p′=100 kPa下的试样(A1～A3)施以不同qd的循环动荷载,对3种影响因素进行探究。考虑到p′、qd和f的影响,将试验结果进行整理归纳,不同试验条件下的累积塑性应变曲线采用文献[18]提出的公式进行预测,得到本文粉砂土的累积塑性变形计算公式,其拟合参数取值见表2所列。累积塑性应变拟合计算公式[18]为:

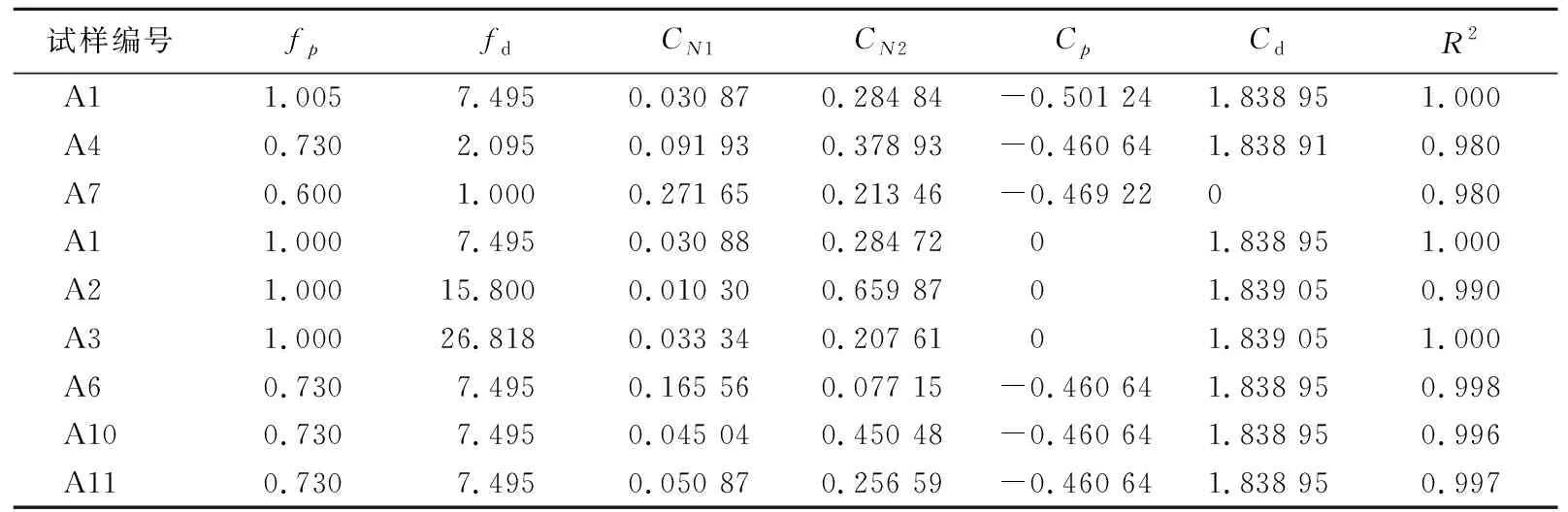
表2 累积塑性应变曲线拟合参数

ε=fpfdCN1[ln(N+1)]CN2,

(1)

2 工程实例隧道地基累积变形数值模拟

2.1 隧道数值模型

采用Midas有限元软件,考虑地铁列车、隧道、地基耦合体系,进行三维数值模型的动力计算,曲率半径R=350 m时地铁隧道数值模型如图5所示。利用有限元模型研究小曲率半径曲线隧道、地铁列车循环荷载作用下粉砂土地层动应力特征,并与1.2节的累积塑性应变拟合曲线结合,考虑列车预测车速v、隧道曲率半径R影响,得到隧道长期累积沉降量的变化规律。耦合体系模型尺寸(X×Y×Z)为180.0 m×120.0 m×68.3 m,隧道内径尺寸为2.7 m,衬砌管片厚度为0.3 m,注浆层厚度为0.15 m,道床厚度为0.55 m,轨道超高为120 mm,轨道位于地下21.5 m深处。每次列车作用下,土体本构采用弹塑性模型,屈服准则为Mohr-Coulomb屈服准则,模型参数由相关土工试验获取,具体取值见表3所列。

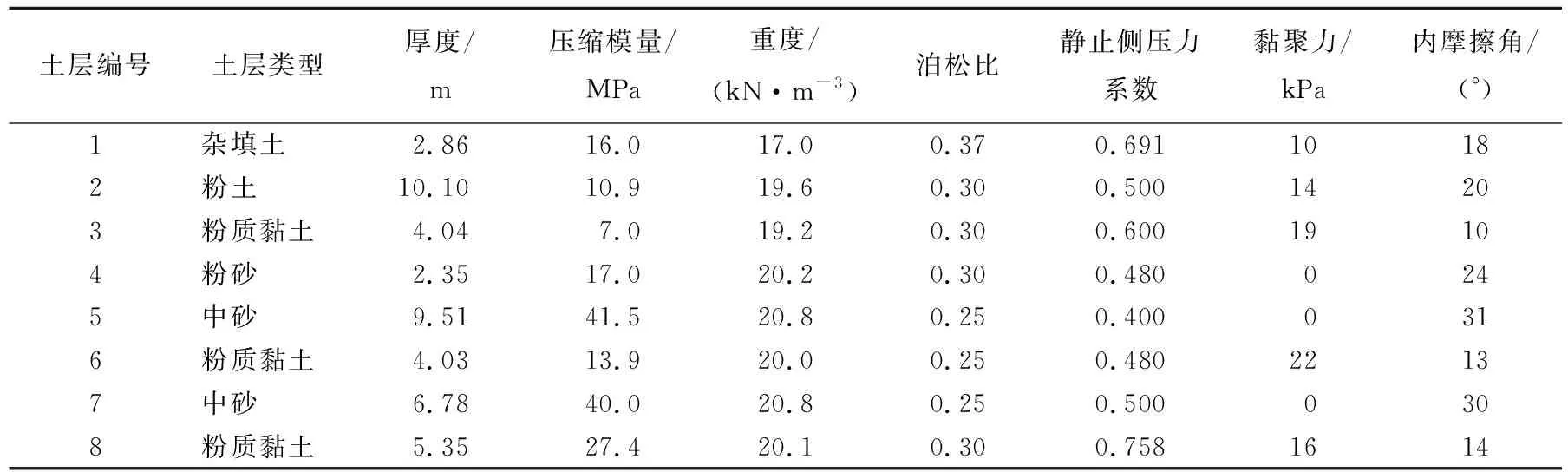
表3 土层物理力学参数取值

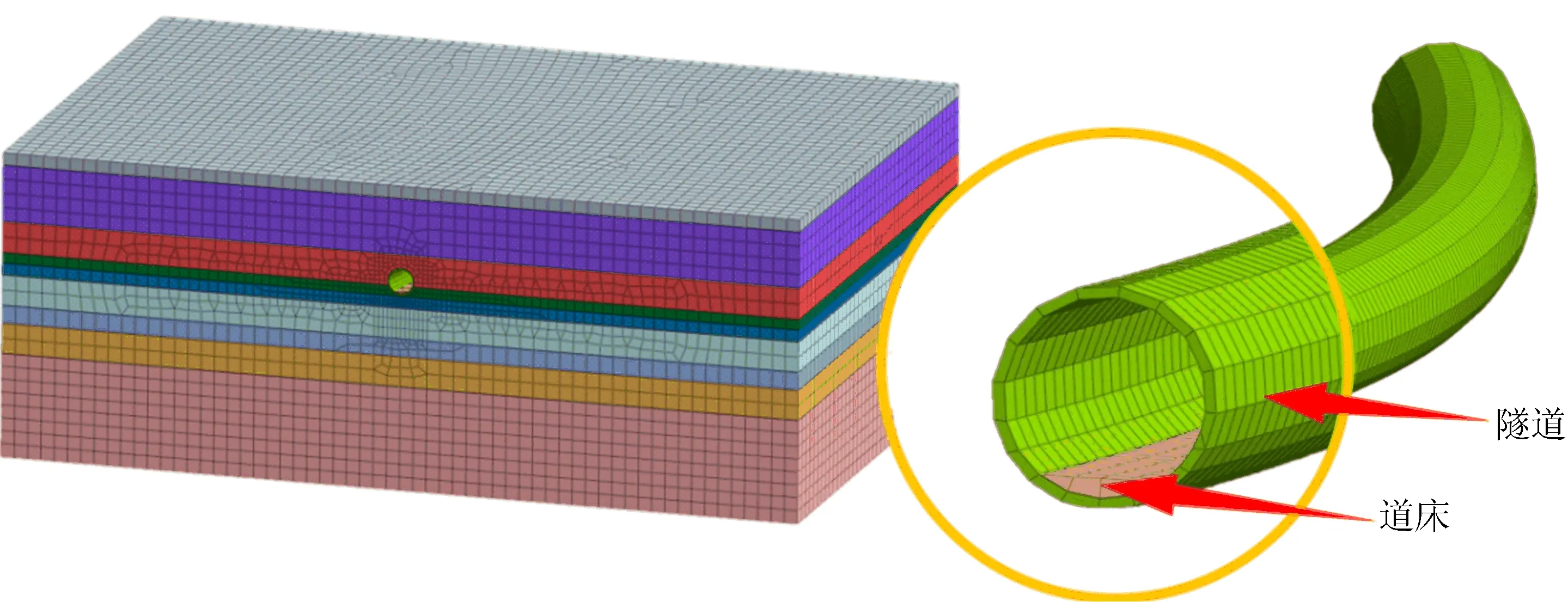
图5 R=350 m时地铁隧道数值模型

列车轴重为13 kN,采用R=350 m、v=80 km/h的模型计算结果与文献[19]结果及实际沉降量进行对比,验证模型正确性。基于该模型,将R、v分别在250～350 m、40～200 km/h内改变,研究R、v2种因素对隧道长期累积沉降量的影响规律。7个模拟工况见表4所列。

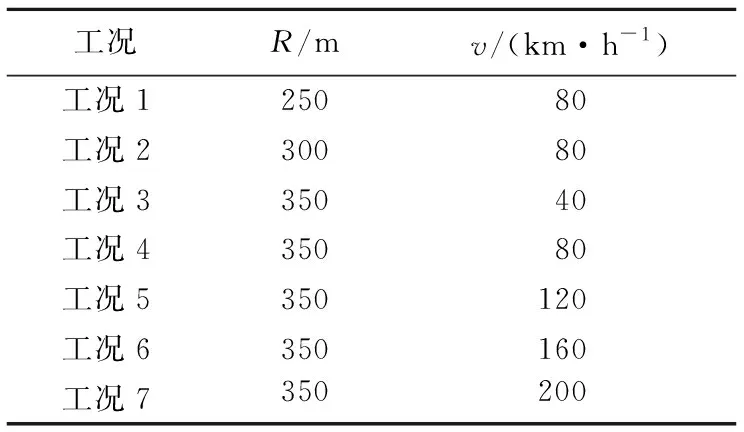
表4 7个模拟工况下的曲率半径与列车速度取值

2.2 路基动偏应力变化规律

为模拟地铁列车运营下循环荷载的动力作用,根据表3土层参数取值,对地铁隧道底部土体进行动力响应计算,提取地基土中的应力分量,其中列车荷载引起的动荷载计算如下:在一定的变形条件下,当受力物体内某点的应力偏张量的第二不变量J2达到一定值时,该点就开始进入塑性状态,即

(σ2-σ3)2+(σ3-σ1)2]

(2)

其中:i=1,2,3;σ1、σ2、σ3为应力偏量的3个主应力。当σ2=σ3时,有

(3)

则动偏应力可计算为:

(4)

第二偏应力不变量还有另一种表达式,即

(5)

最终动偏应力计算公式为:

(6)

其中,σxd、σyd、σzd、τxyd、τyzd、τzxd为列车循环荷载作用产生的应力分量。

R=350 m时,不同车速下的动偏应力qd变化如图6所示。从图6可以看出:随土体深度增加,动偏应力整体呈现逐渐减小的趋势,这与文献[19]结果相同,验证了本文数值模型的正确性;随着车速增大,相同深度处的动偏应力逐渐变大,且距离隧道底部越近,变化越大;80、120 km/h下最大动偏应力相比于40 km/h下分别增加0.4%、5.6%;在隧道底部2 m范围内,动偏应力的变化趋势受车速影响,当车速在40～120 km/h内,动偏应力随深度增加先增大后减小,而当车速增大到160 km/h后,动偏应力直接由峰值点逐渐减小;在距隧道底部约10 m深度处的第6层粉质黏土中,动偏应力曲线又出现先增加再减小的现象,这是由于该层土较软,压缩模量急剧降低,与上下砂土层性质差别较大。

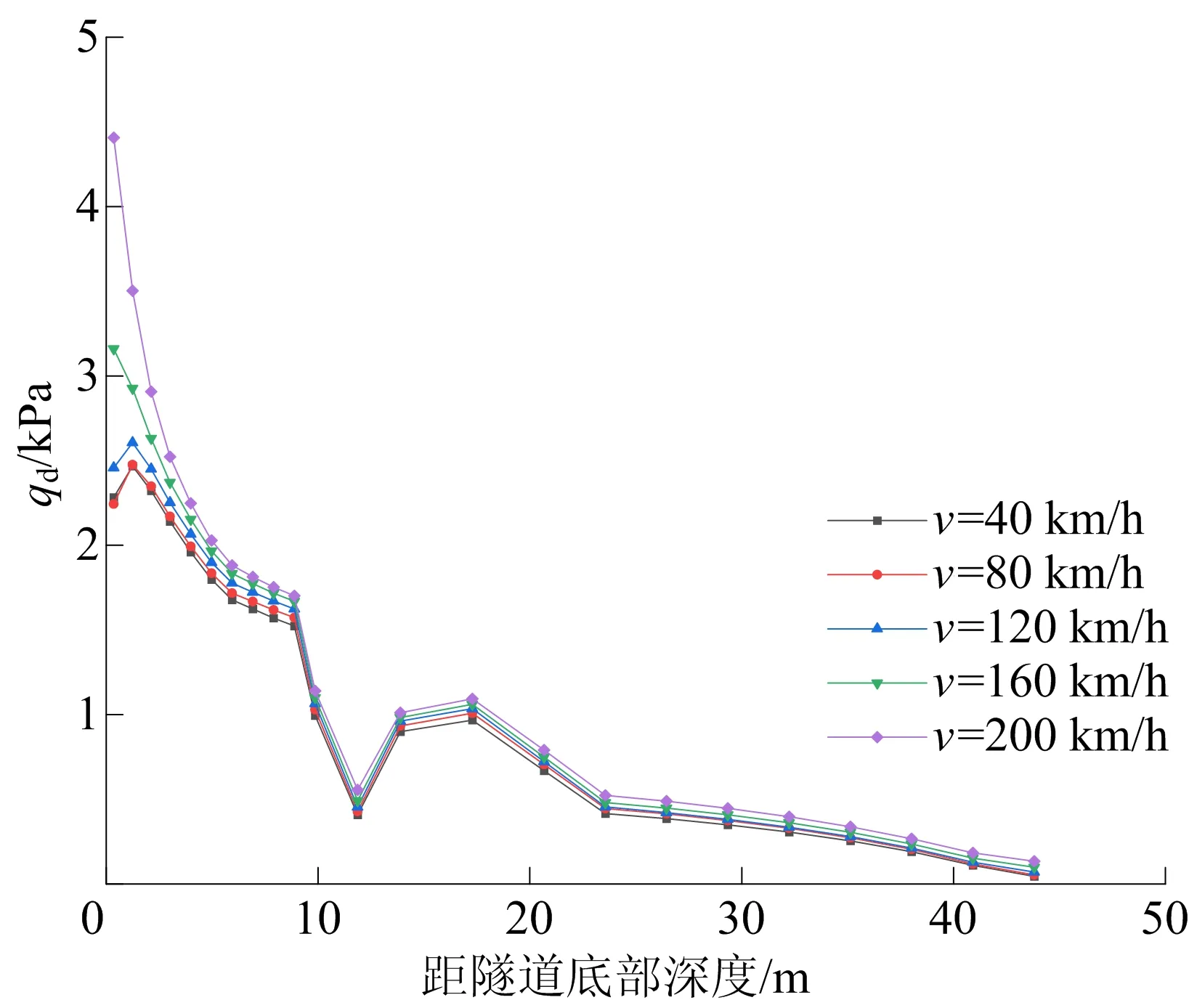
图6 R=350 m时不同车速下qd随深度变化曲线

v=80 km/h时,不同曲率半径下qd随深度变化曲线如图7所示。从图7可以看出:与不同车速下动偏应力的变化相比,不同曲率半径下的动偏应力变化幅度更小;相同深度条件下,3种曲率半径下的动偏应力相差不大;动偏应力大小与土层类型也有较大关系,在粉质黏土层范围内,会出现动偏应力先上升再下降的现象,与图6不同车速下的变化规律类似。

图7 v=80 km/h时不同曲率半径下qd随深度变化曲线

总体而言,动偏应力对车速的敏感性要大于对隧道曲率半径的敏感性。

2.3 隧道地基长期沉降预测

结合有限元计算结果与试验累积变形拟合公式,对隧道底部土体长期沉降进行预测。根据2.2节得出的动偏应力,采用分层总和法计算每层土的累积沉降,获得考虑不同车速和不同曲率半径影响下隧道地基长期沉降规律。按郑州轨道交通1号线每天运行列车192列,每列车为6节编组计算,同一位置每天约振动4 608次,每年约振动168×104次。

文献[17]对大曲率半径(R为350～1 000 m)隧道沉降值的研究表明,R增大,沉降量减小。本文选取小曲率半径(R为250～350 m)进行研究,从而获得更大范围曲率半径的影响。土层累积沉降计算公式[20]为:

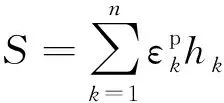
(7)

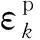
模拟工况4(R=350 m,v=80 km/h)下,地基长期沉降计算值与实际沉降对比如图8所示,不同车速、不同曲率半径下土体长期沉降预测结果如图9所示。

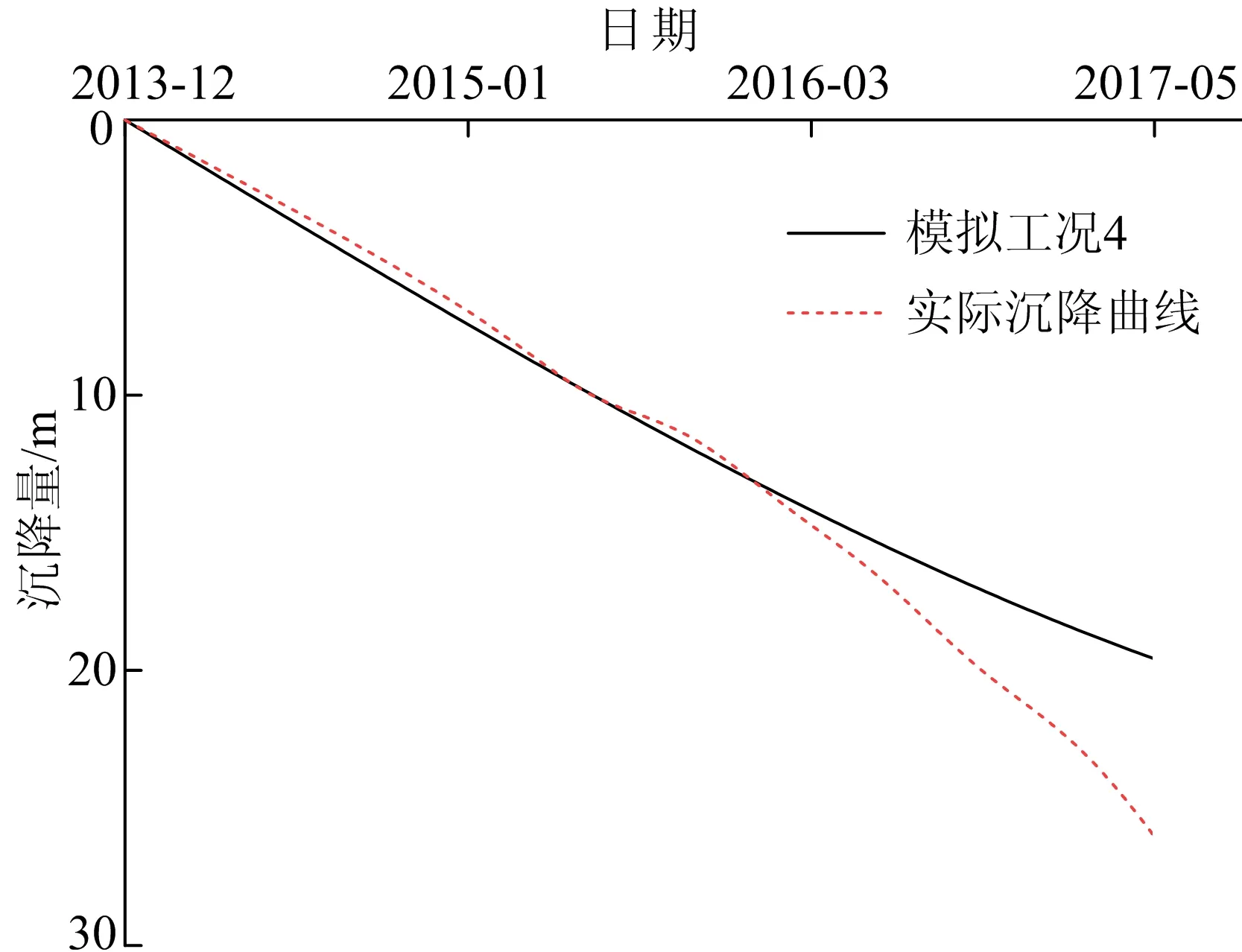
图8 模拟工况4地基长期沉降计算值与实际沉降对比

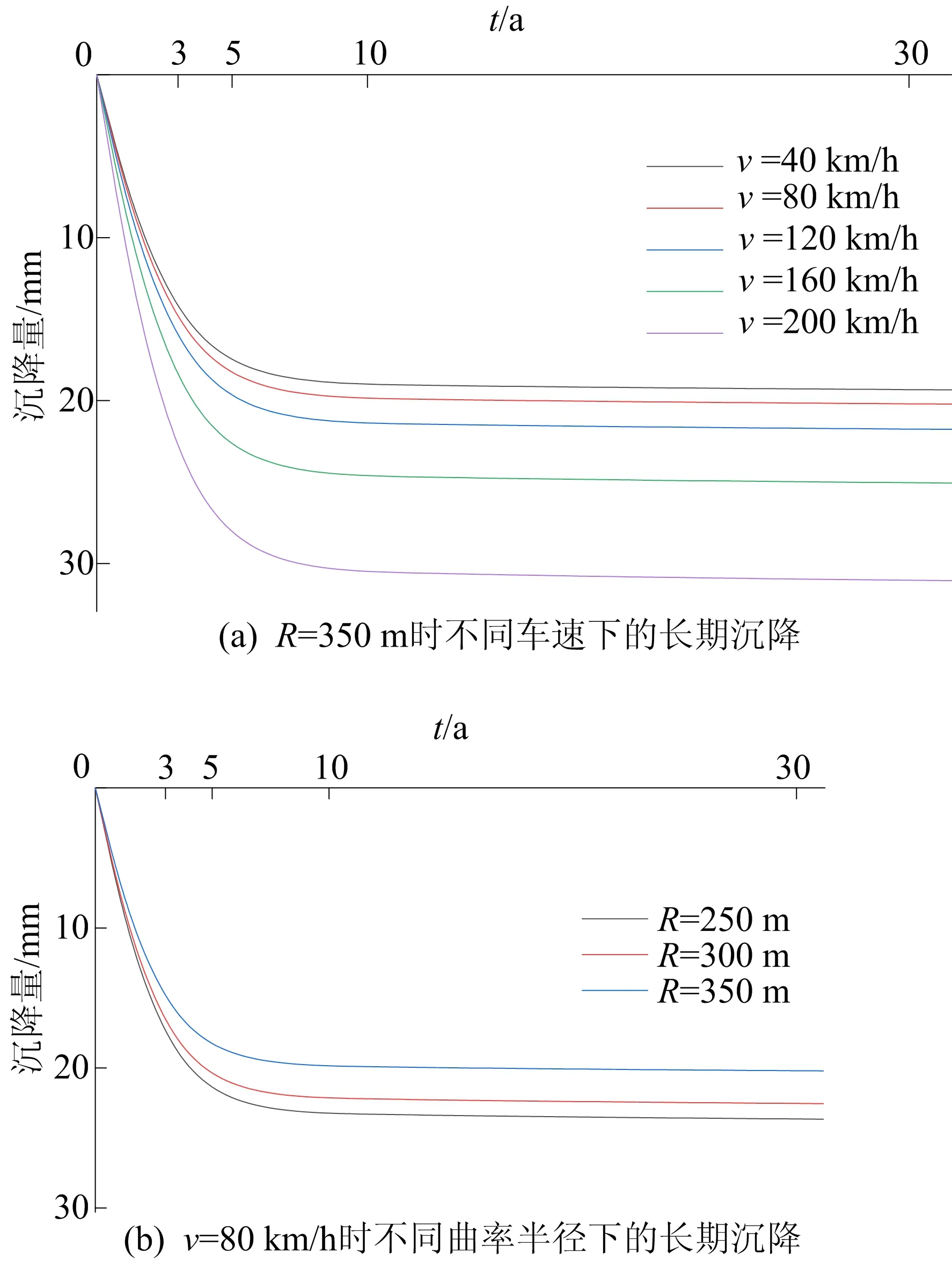
图9 不同车速、不同曲率半径下土体长期沉降预测结果

本文表4中的模拟工况4与实际工况一致[17],从图8可以看出,通车3 a内模拟沉降值与实际沉降结果较吻合。

由图9a可知:在初始的5 a内沉降迅速发展,随后逐渐趋于稳定;车速越大,沉降发展越快,最终稳定值也越大;在40～120 km/h之间,沉降变化较为平缓,且稳定在1.56 mm以内;在车速超过120 km/h后,沉降稳定值迅速增大,变化幅度最大可达6 mm,由此可见,列车的高速行驶对于地基沉降影响明显。

从图9b可以看出:在地铁运行最初3 a,土体沉降较大,3条沉降发展曲线基本重合,第3年时达到19.58 mm;在运行3～5 a时,沉降值开始发生较大差异,沉降速率减小,且最后趋于稳定,隧道曲率半径越小,稳定沉降值越大;R为250、300、350 m下最终稳定沉降值分别为23.68、22.57、20.23 mm,最大沉降差值为3.45 mm。

由图9a、图9b可知,R=250 m、v=80 km/h下最终稳定沉降量为23.68 mm,R=350 m、v=120 km/h下最终稳定沉降量为21.78 mm,前者大于后者。由此可见,曲线隧道的曲率半径对隧道地基长期沉降影响更大,这是由于小曲率半径隧道,地铁列车引起的横向荷载加大,造成土体沉降也变大。因此,要综合考虑曲率半径和列车速度的影响,当曲率半径为250～350 m时,列车速度控制在80 km/h以下,而当曲线隧道曲率半径大于350 m时,列车速度可适当调高。

3 结 论

本文通过大振次的粉砂土三轴试验,考虑有效固结应力、列车振动频率、列车动应力幅值等影响因素,提出黄泛区郑州粉砂土的累积塑性变形发展计算公式;基于实际工况,建立隧道、轨道、地层的三维数值模型,计算不同列车速度和隧道曲率半径影响下、列车荷载作用下地层实际动应力,并代入本文提出的累积变形公式中,预测不同列车速度和不同曲率半径影响下的长期累积变形,将预测结果与现场实测结果进行对比,得出以下结论:

(1) 大振次的粉砂土动三轴试验结果表明,在动荷载作用下粉砂土随振动次数增加,其应变曲线经历急剧增长、缓慢增长、趋于稳定3个阶段,相较于软黏土,急剧增长阶段粉砂土产生的变形量更大,变形速率更快,更易因振动而发生变形破坏。土体长期沉降预测曲线也呈现此3个变化阶段。

(2) 数值模拟结果表明,列车行驶速度越快,曲率半径越小,引起隧道地基中的动偏应力越大,更大的动偏应力对于隧道结构和周围土体都会产生不利影响。动偏应力对列车速度的敏感性要大于对隧道曲率半径的敏感性,80、120 km/h下最大动偏应力相比于40 km/h下分别增加0.4%、5.6%。理论上,建议列车通过曲率半径为250～350 m路段时速度控制在80 km/h以下。

(3) 由数值模拟可知,曲线隧道的曲率半径和列车运行速度对隧道底部土层长期沉降均有影响,且隧道曲率半径大于300 m、列车速度大于120 km/h后的影响更大,整体而言,列车速度影响更大。曲率半径越小,土体沉降值越大,在地铁

运营初始3 a内引起的沉降较大,第3年时达到19.58 mm;运行3～5 a土体沉降速率减小,最后基本趋于稳定;曲率半径为350 m下,到达设计年限30 a时,沉降稳定于20.23 mm。根据本文研究结果,并考虑规范中的沉降控制值[21]25 mm,综合考虑曲率半径和列车速度的影响,当曲率半径为250～350 m时,列车速度宜控制在80 km/h以下,而当曲线隧道曲率半径大于350 m时,列车速度可适当调高。