“数学工具与实验”课程教学方式研究
2023-05-30吴昊谢雅洵
吴昊 谢雅洵
关键词:MATLAB;数学实验;措施;算法案例;教学策略
中图法分类号:G642 文献标识码:A
1引言
“数学工具与实验”是数学与应用数学专业非常重要的一门专业必修课程,该课程具有较强的抽象性、实践性,除了必须理解和掌握相关的数学知识,还需要应用MATLAB编程对这些知识加以呈现,对学生的数学思维和编程能力均有较高的要求,因此导致很多学生在学习这门课程时产生学习目的不明确、不知该如何动手编写程序、理论和实际脱节等情况。此外,“数学工具与实验”课程对提高学生的数学应用能力、分析和解决问题的能力均有较大帮助,并且还可以提升学生参加“华数杯”全国大学生数学建模竞赛、全国大学生数学建模竞赛等竞赛的竞争力。
目前,国内已有很多学者对该课程及其相关课程的教学模式做了一些研究,但研究的侧重点均有所不同。霍录景对独立学院数学实验课程的教学内容、教学方式和考核方式做了一些具体的研究。卢月莉通过数学实验中的一些具体案例,讲解了MATLAB编程的具体实现过程。杨然通过使用MATLAB符号,有效解决了高等数学中的许多计算问题,提高了學生的学习兴趣及编写程序的能力。梁燕来等针对应用型本科院校,提出了数学专业数学实验课程教学改革思路。王慧敬等从培养应用型本科人才的角度出发,探讨了开设数学实验课程的意义、课程的设计目的与讲授内容。马国栋等给出了数学实验融人课堂教学的几个实验的实现过程,并给出了教学改革的几点建议。董鸽等以中药材质量鉴别中的数据分析为例,用MATLAB实现了对数据的主成分分析,阐明可根据专业选取合适的教学内容。刘利斌等对数学实验类课程的教学现状进行分析,并给出了一些课程教学改革的建议。贾丽丽对数学实验课程现状进行了分析,并给出了相应的课程建设方案。黄小玲等提出了改革和创新数学实验课程方式的4个方面,主要包括区别“数学实验”与数学、加强编程指导、结合实例教学及引导网络学习。陶淑一提出了数学实验的分层教学设计,并给出了“交通流量问题”的分层教学设计过程。
针对以上学者的研究发现,大多数研究仅局限于课程的教学方法、教学内容、某个教学知识点的实现过程等,但对教学策略的探讨,以及如何提高学生的算法思维和编程能力的研究还比较少。本文将具体针对“数学工具与实验”课程中的教学策略、算法分析和编程教学做一些探讨。
2教学措施
在从事“数学工具与实验”课程的教学中,通过自身的探索以及和学生的交流,不断改进该课程的教学方法。同时,要使教学内容具有科学性与先进性,让学生看到学科的实用价值,并开阔学生的视野。此外,在教学的过程中,要以学生为主体,引导学生树立正确的学习观,课程教学采用启发式、案例式、问题导向式等多种教学模式,培养学生学习的积极性,激发学生学习的热情,加深学生对本课程的理解和认识,具体做法如下。
(1)加强实践环节的训练,有针对性地布置一些课后实验让学生自主练习,同时要加强对学生课后实践的检查,通过课堂提问、安排学生自主讲解实验过程、小组协作和互助等方式监督学生的学习状况。
(2)在教学的过程中,可以采用先易后难的教学策略,实验的设计从简单到复杂,即程序的实现先从简单的指令,再到一个程序模块,最后到一段完整的程序代码;在上机的过程中,先写好程序让学生照着程序写代码,完成后让学生理解,再到不看程序写代码,最后到学生独立自主地编写程序。
(3)对课程中的算法问题,要举一反三地讲解。不但要讲解算法思想、编程思路、程序实现,还要结合某一案例,把算法的思想及程序的实现过程有机结合起来,让学生了解程序在具体应用中的实现过程,加深学生对算法的理解,提高学生分析问题和解决问题的能力。
(4)通过以赛促教的方式,加强学生学习的动力。在讲到课程的某些知识点时,可以穿插“全国大学生数学建模竞赛”中的一些题目,让学生意识到MATLAB编程在竞赛中所起到的作用,提高学生学习的积极性。
(5)加强课程考核的引领作用,期末考试以试卷考核和实验考核相结合的方式检查学生对课程内容的掌握情况,并在日常的教学过程中,实时公布学生在课堂实验中所取得的平时成绩。
(6)注重课程教学后的总结和反思,及时发现课程教学过程中存在的问题。在学期末安排学生撰写学习本门课程的学习心得,并和学生交流,发现课程教学过程中存在的不足,为后续的教学提供更充足的准备。
3算法案例的教学策略
算法案例是“数学工具与实验”课程与编程结合较为紧密的一个教学环节,然而算法是比较抽象且不易理解的,在教学的过程中,可以把算法的描述简单化,算法的流程清晰化,算法的实现过程层次化,一步一步把算法的思想贯穿给学生。具体的做法如下。
(1)用学生容易理解的语言和方式重新描述算法,让学生理解算法的实现过程及实现的关键环节。
(2)用流程图来表示算法,使算法的思想变得更加清晰。
(3)根据算法的流程,用MATLAB编写程序实现算法,在程序的编写过程中要清晰地标注每一层的实现及每条语句的作用,让学生在查阅程序时有非常直观的印象。
(4)结合一个比较简单的具体实例,带领学生模拟运行一下程序的执行过程,加深学生对算法思想的直观理解。
以Dijkstra算法为例,讲解该算法在教学过程中具体实现的过程,具体做法如下。
3.1算法的描述
步骤1 初始化S,l,z(S集合为已找到最短路的顶点集合,S非集合为还未找到最短路的顶点集合,l集合为顶点到固定顶点的一条路径权值,z集合为顶点的父亲顶点)。
步骤2 用新并入S集合中的顶点(该顶点记为v),更新S非集合中的顶点(依次取,记为u)。若v的l值大于u的l值及v,u权值之和,则令v的l值等于u的l值加上v,u权值之和,v的z值等于u。
步骤3 在S非集合中找l的取值最小的顶点,并把该顶点并入S集合中。
步骤4 判断S非集合是否為空,不为空,转步骤2继续执行;否则,算法结束。
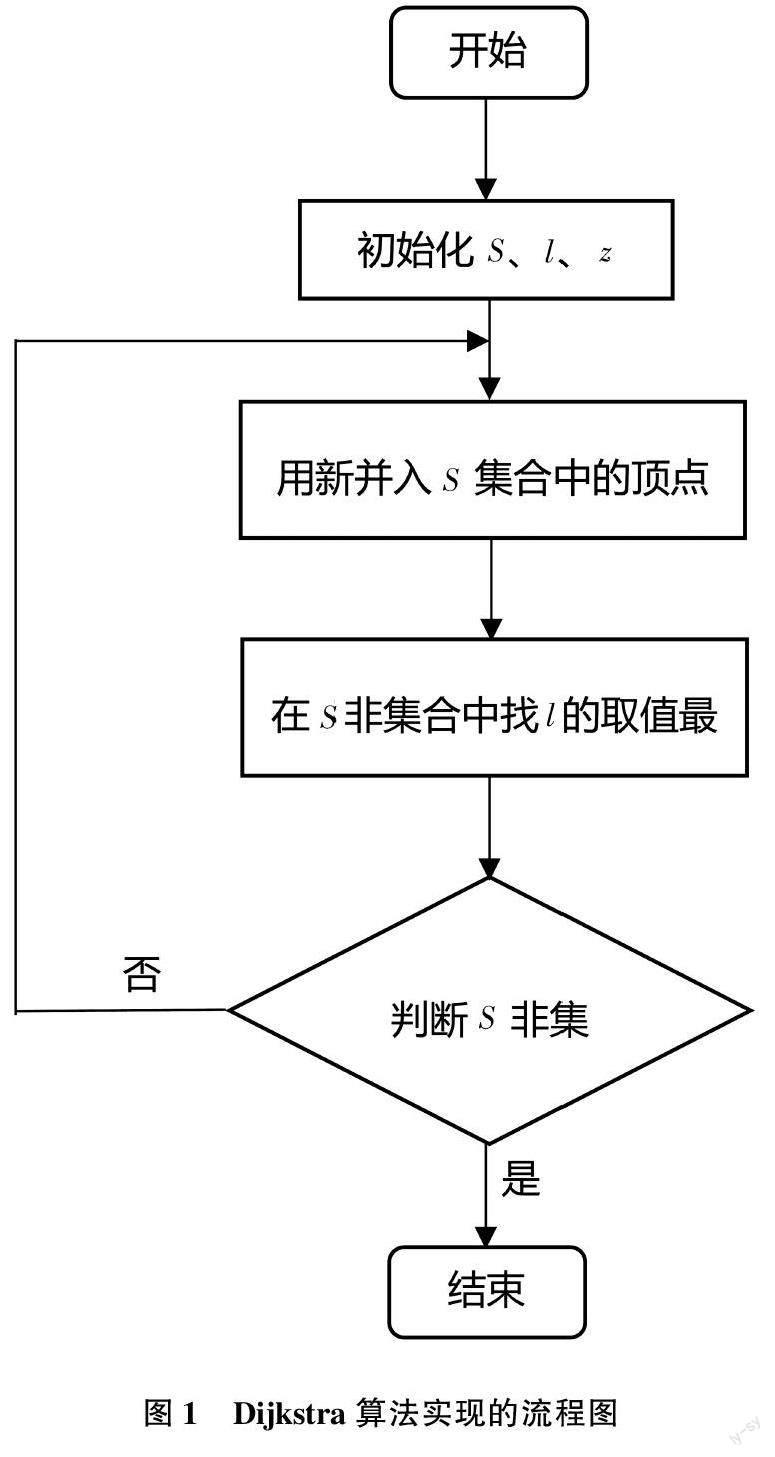
3.2算法实现的流程图
根据算法的描述,画出Dijkstra算法实现的流程图,如图1所示。
3.3算法的程序描述
本文算法的实现过程主要是按照算法的思想一步一步实现的,其实现的流程和算法描述的流程一一对应,层次分明,并且在程序中清晰地标注所实现的每一层及每条语句的作用,具体程序的书写过程如下。
%第一层:赋初始值,对应算法步骤1
n= size(w,1);
%n是图的顶点个数
wl=w(l,:);%w1是u0到其余顶点的权值
l(1:n)= wl(l:ri); %对l赋初值
z= ones(1,n); %对z赋初值
s=[]; %s用来保存已找到最短路径的顶点
s(1)=1;%把固定顶点的下标存到s集合中
u=s(1); %u用来保存s中最后一个元素的下标
k=1; %k用来保存s中最后一个元素的下标
%下面的代码是用来把剩下的n-1个顶的最短路径找出来
while k
%第二层:用新并入S集合中的顶点更新S非集合中的顶点,对应算法步骤2
for i-l:n %
if i~=s(l:k) %找不在s中的顶点
ifl(i》l(u)+w(u,i) %判断v的l值是否大于u的l值及v,u权值之和
l(i)=l(u)+w(u,i); %修改不在s中顶点的l值
z(i)=u;%修改
不在s中顶点的z值
end
end
end
%第三层:在S非集合中找l的取值最小的顶点,对应算法步骤13
lv= inf; %1v用来保存不在s中的顶点的最小1值,v用来保存对应的下标
for i-l:n %
if i~=s(1:k)
%找不在s中的顶点
if l(i)
lv =l(i);
v =1;
end
end
end
k=k+1:
s(k)=v; %把找到的顶点并入S集合中
u=s(k);
end
以上程序代码在实现时将算法思想和程序结合,层次分明,逻辑结构清晰,同时标注出算法实现的关键点,方便学生对算法的理解以及对程序的阅读,对于学生提高编程的能力及编程习惯的养成均有帮助。
4结束语
“数学工具与实验”课程的教学任重而道远,学生学完本课程后,能够利用MATLAB程序来实现一些基本的应用。由于本课程需要学生编写程序,所以在教学过程中,应把程序实现和相关的数学知识相结合,便于学生对本课程知识的理解和掌握。同时,对于算法案例的教学,一定要采用合适的教学策略,把抽象的算法思想转化成学生易于理解的方式,使程序设计流程尽量和算法思想相对应,最终达到比较理想的教学效果。
作者简介:
吴昊(1982—),硕士,讲师,研究方向:嵌入式系统、智能算法。
谢雅洵(1991—),硕士,讲师,研究方向:数值计算(通信作者)。
